持续可变载荷条件下液压泵故障信号的多尺度形态滤波分析

刘思远, 王　闯, 姜万录, 张文文

(1．燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北　秦皇岛　066004；2．燕山大学 先进锻压成形技术与科学教育部重点实验室,河北　秦皇岛　066004)



持续可变载荷条件下液压泵故障信号的多尺度形态滤波分析

刘思远1, 2, 王闯1, 2, 姜万录1, 2, 张文文2

(1．燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北秦皇岛066004；2．燕山大学 先进锻压成形技术与科学教育部重点实验室,河北秦皇岛066004)

摘要：改变液压系统载荷的大小会使液压泵振动信号的幅值发生变化，从而引起信号振动特征发生改变，因此，单一尺度结构元素的数学形态学方法对液压泵变载荷条件下的信号滤波不一定有效。为此在单尺度形态分析方法的基础上，同时兼顾长度(时间)和高度(幅值)两种尺度对持续可变载荷条件下泵的振动信号进行多尺度形态滤波。以冲击特征比值和二阶原点矩为特征指标构建的复合评价体系为依据，提出结构元素长度和高度尺度的寻优方法。对持续可变载荷条件下的液压泵进行了故障模拟试验，检验了多尺度形态分析方法对液压泵正常状态、单柱塞滑靴磨损以及中心弹簧失效三种不同状态信号的滤波效果。通过与单尺度形态滤波方法相比较，证实了多尺度形态滤波方法更适合于处理液压泵变载荷条件下的振动信号。

关键词：持续可变载荷；多尺度；形态滤波；液压泵

实际工程中所用的液压系统由于受到工作阻力、动载荷、剧烈振动等偶然性因素的影响，多数都工作在变载荷工况条件下。近年来，研究液压系统振动信号的滤波方法有很多，但多以定载荷工况为前提，与实际的变载荷工况条件有很大差别。并且，载荷的变化会引起液压泵振动信号的特征发生变化，使传统方法的滤波效果变差，增加了信号滤波处理的难度。西安交通大学的林京教授在2014年全国设备监测诊断与维护学术会议的专题报告上指出，“机械信号的非平稳性会受到运行工况的显著影响，脱离工况谈故障诊断是无稽之谈”。因此，研究变载荷工况下液压系统振动信号的滤波方法对丰富液压系统故障诊断的理论体系，提高故障诊断方法的实用价值具有重要的理论意义和广阔的应用前景。

目前，在液压系统振动信号的滤波方法研究方面，很多都以液压泵为研究对象。学者们在机械工程、航空航天等领域开展了大量的有关液压泵故障信息滤波技术的研究工作[1]。王少萍等[2]采用小波包分析技术对液压泵出口振动信号进行了消噪处理，解决了泵出口故障检测信号信噪比低、难以进行故障特征提取的问题。姜万录等[3]利用小波分解重构算法对液压泵故障的振动信号进行分解、去噪和重构，有效增加信噪比的同时，对故障特征信号进行了时域定位。刘玉娇等[4]利用粒子滤波算法实现了对液压泵振动信号的有效降噪。李志兴等[5]研究了基于小波包的降噪方法，证实了小波包分析能够根据被分析的液压泵振动信号特征，自适应地选择相关的频带，提高信号的时-频分辨率，突显故障信息。虽然上述方法在定工况条件下都取得了较好的滤波效果，但是并未开展针对变载荷工况条件下的相关研究工作。

轴向柱塞泵故障振动信号十分复杂，常常表现出非线性、非高斯和非平稳性特征，给信号滤波和特征提取带来了很大困难。数学形态学是近年来发现的处理该类信号较为行之有效的方法。姜万录等[6]提出了一种确定最优扁平型结构元素长度的形态滤波方法，并在液压泵故障振动信号的滤波过程中得到了较好的应用效果；李扬[7]针对液压泵振动信号提出了基于最优结构元素长度的形态滤波方法，并在此基础上又研究了基于限定阈值的自适应多尺度形态滤波方法，滤波效果同样得到了较好的印证。因此本文将在以上研究成果基础上，确定以冲击特征比值和信号故障特征频率到零频段频率幅值的二阶原点矩为特征指标来构建复合评价体系，提出对长度和高度尺度进行寻优的形态滤波方法；通过仿真分析给出该方法具体实现步骤；通过持续可变载荷条件下液压泵故障模拟试验，验证该方法对持续可变载荷液压泵振动信号滤波的有效性。

1多尺度形态学分析方法基本原理[8]

1.1多尺度形态运算[9]

数学形态学是20世纪60年代由法国Matheron和Serra 提出用来处理图像的理论，之后Maragos和Shafer将其扩展到对一维信号的滤波处理中[10-12]。在用于一维信号处理时，结构元素的尺度信息包括长度和高度两个因素，所采用的结构元素由长度尺度λl和高度尺度λh共同确定。多尺度形态学分析中的结构元素尺度信息为λ=(λl,λh)。

Tλ(X)=λT(X/λ)

(1)

同理，多尺度腐蚀和膨胀运算表示为：

(XΘB)λ=λ[(X/λ)ΘB]=XΘλB

(2)

(X⊕B)λ=λ[(X/λ)⊕B]=X⊕λB

(3)

式中：λB=B⊕B⊕…⊕B(λ-1次膨胀运算)。

由此，通过腐蚀和膨胀运算可以构成四种基本运算算子T，即腐蚀、膨胀、开运算和闭运算。多尺度运算就是将T中所有腐蚀、膨胀变换所使用的B进行λ-1次膨胀运算。

1.2差值滤波器[6]

以四种基本形态算子T为基础，根据液压泵故障呈现的冲击特征，构建差值滤波器模型。差值滤波器模型结构为

f•g-f ○g=(f•g-f)+(f-f ○g)

(4)

式中：f•g-f被称为形态学的黑Top-Hat变换，用于提取信号中的负冲击；f-f○g被称为形态学的白Top-Hat变换，用于提取信号中的正冲击。

1.3冲击特征比值[7]

形态滤波器的参数设置会严重影响信号滤波的效果。为此定义冲击特征比值来定量分析形态滤波频域特征的提取效果：

(5)

式中:fi是特征频率的i倍频对应的功率谱密度峰值，M是最高倍频数，取M=3；N是总谱线数。K为频域中信号特征频率与其余频率的比值，K值的大小反映了信号特征频率在频谱图中的突出程度。K值越大，则特征频率越突出，特征提取的效果越好；K值越小，特征频率越不明显。

2多尺度形态学滤波效果的仿真分析

设定如式(6)所示的含噪仿真信号，用于模拟幅值突然发生改变时液压泵的故障信号[11]。

x(t)=x1(t)+x3(t)•x2(t)+x4(t)

(6)

式中:x1(t)是频率为16 Hz的周期性指数衰减信号，每周期内冲击函数为8e-500tsin(512πt)，用于模拟故障信号，如图1(a)所示；x2(t)为频率为20 Hz低频谐波信号，其表达式为x2(t)=cos(40πt)；x3(t)是某一矩形波函数信号，表达式为x3(t)=1(t-0.5)-1(t-0.625)+1，用于模拟在0.5～0.625 s时间段信号幅值突然增加到原来的2倍，如图1(b)所示；x4(t)是标准差为1的高斯白噪声，用于模拟强背景噪声。

设定采样频率为2 048 Hz，截取采样时长为1 s。图1(c)是混合信号的时域波形，从图中很难分辨脉冲成分。从图1(d)中可以看出，冲击信号被谐波信号和高斯白噪声信号完全淹没，无法通过原始信号功率谱图发现冲击信号的特征频率成分。

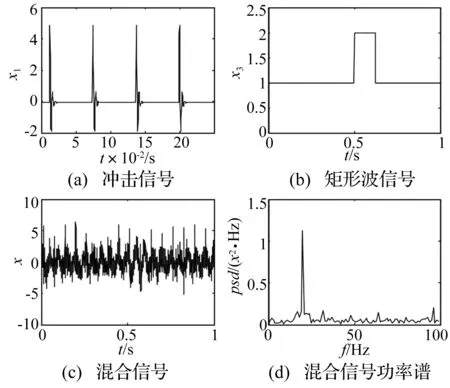
图1　故障仿真信号Fig.1 Fault simulation signals

2.1结构元素对形态滤波效果的影响分析

(1) 结构元素形状对形态滤波效果的影响

从图2可以看出随着λh的增大，三角形结构元素对应的冲击特征比值有明显的提高，而半圆形和扁平形没有任何变化。由此说明，选择三角形结构元素通过增加λh可以更有效地提高形态滤波的效果。

图2　不同结构元素形状对应的冲击特征比值Fig.2 The impact characteristic ratio of different structural element shapes

(2) 长度尺度对形态滤波效果的影响

设计差值滤波器，基本元素形状选取为三角型，只考虑结构元素长度尺度变化时分析仿真信号x(t)的形态滤波效果(λh设为1)。滤波后的功率谱如图3所示。

从图3中可以看出，增加长度尺度可以有效抑制噪声信号，且尺度越大噪声抑制的效果越好。但是，16 Hz倍频处的特征频率峰值随λl的增加越来越不明显。当尺度增加到39时，在0～16 Hz频率间意外出现较多的干扰频率，而且更多的倍频信息丢失。由此看出，盲目增大长度尺度显然无法获得好的滤波效果。

图3　长度尺度不同时形态滤波信号的功率谱Fig.3 Power spectrum of morphological filtering signal with different length scales

(3) 高度尺度对形态滤波效果的影响

设计差值滤波器，基本元素形状选取为三角型，只考虑结构元素高度尺度变化时分析仿真信号x(t)的形态滤波效果(λl设为15)。滤波后的功率谱如图4所示。

从图4中可以看出，随着高度尺度的增加，16 Hz及其倍频处的特征频率对应峰值有明显的增长。这说明，高度尺度在一定范围内的增加可以有效提高该类仿真信号的形态滤波效果，且不会出现干扰频率和倍频减少的现象。

图4　高度尺度不同时形态滤波信号的功率谱Fig.4 Power spectrum of morphological filtering signal with different height scales

(4) 多尺度寻优

利用故障特征频率到零频率幅值的二阶原点矩作为特征指标，适当控制其数值大小可以避免由于盲目增加λl带来的干扰频率和倍频减少现象的发生。因此，可将该指标与冲击特征比值一同纳入形态滤波效果的评价体系中联合评价形态滤波效果的好坏[7]。

图5是λh=1时，冲击特征比值和二阶原点矩随λl变化的特征曲线。从曲线中可以看出，随着λl的增加，冲击特征比值在λl(0,16)区间内有较大的波动；在λl(16,22)区间内较为稳定；而在λl大于22区间有明显的下降趋势。虽然在λl=4和λl=18时都能获得较大的冲击特征比值，同时也能得到较小的二阶原点矩，但是λl=18处对应的冲击特征比值变化更稳定。因此可取λl=18为寻优后的长度尺度。

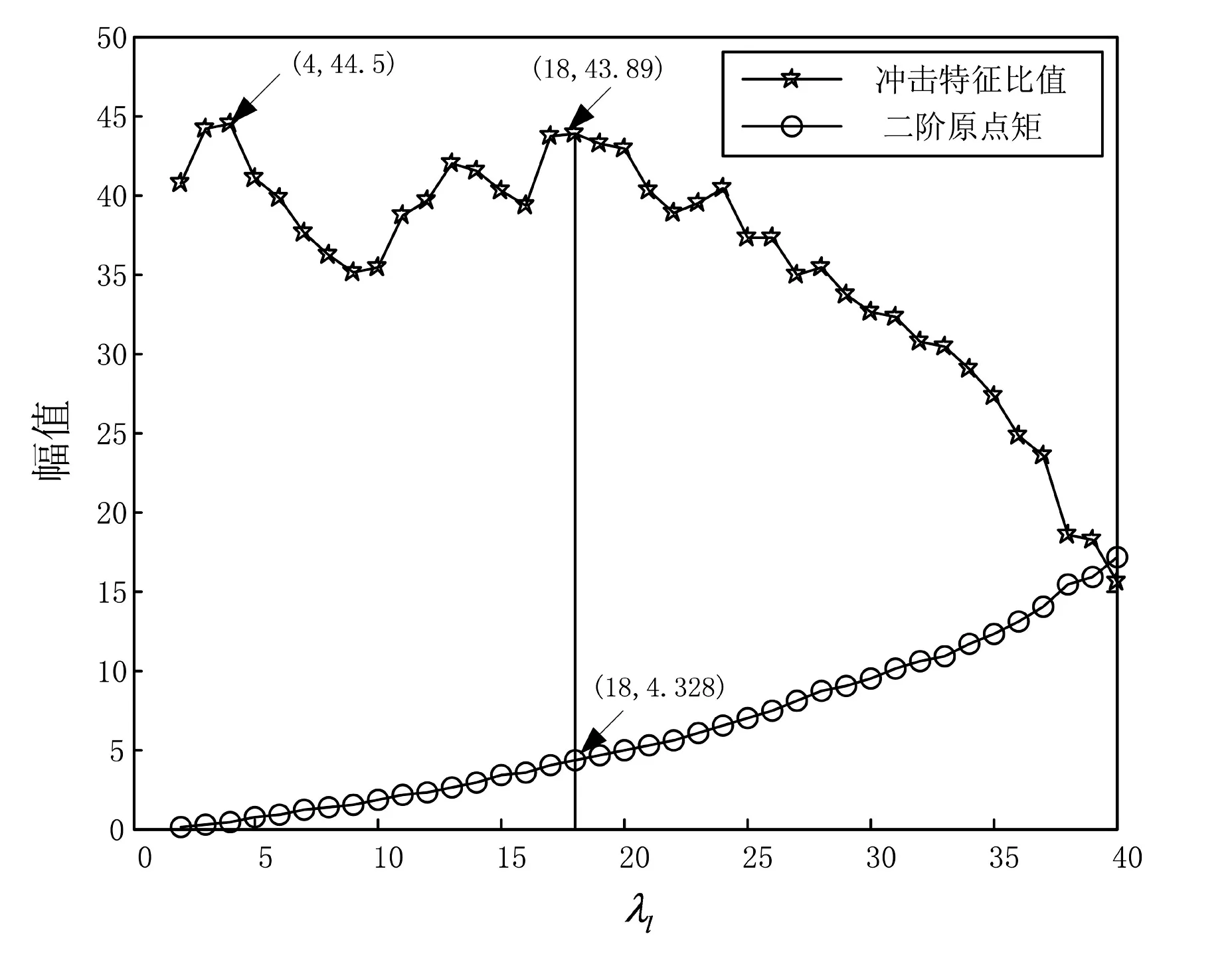
图5　结构元素长度尺度寻优曲线Fig.5 Optimization curves of the structural elements length scale

对λl=18时的形态滤波信号进行分析，图6是冲击特征比值和二阶原点矩随λh变化的特征曲线。由图可知λh=69时冲击特征比值达到最大值，因此可取λh=69为寻优后高度尺度。

图6　结构元素高度尺度寻优曲线Fig.6 Optimization curves of the structural elements height scale

2.2多尺度形态滤波效果分析

同时考虑长度和高度尺度变化对形态滤波效果的影响，确定最优长度和高度尺度参数组合λ=(18,69)，得到多尺度形态滤波后的功率谱图，如图7(a)所示。引用文献[7]提出的基于最优结构元素长度的单尺度形态滤波方法得到最优结构长度为λl=5,由此得到滤波信号功率谱如图7(b)所示。

图7　两种方法滤波的信号功率谱分析Fig.7 Signal power spectrum analysis of the two methods filtering

对比两个谱图可以发现，经过长度和高度结构元素多尺度寻优后的仿真信号功率谱在16 Hz及其倍频位置特征频率对应峰值很明显，而利用文献[7]的方法仅对长度进行寻优后的功率谱在16 Hz特征频率5倍频和6倍频位置处的峰值很不突出。

通过信噪比的计算得出多尺度形态滤波信号的信噪比为16.4高于单尺度形态滤波信号的信噪比9.3。

由此证明，文中提出的多尺度形态滤波方法相比文献[7]中的滤波方法更适用于对变幅信号进行特征提取，具有较高的信噪比和较好的滤波效果。

3多尺度形态学滤波方法

本文在文献[7]方法的基础上进行了改进，同时兼顾长度和高度两种尺度对持续可变载荷作用下泵的振动信号进行多尺度形态滤波。具体方法实现的步骤如下：

(1) 采集振动信号，构建一维离散时间向量；

(2) 确定最优结构元素形状，建立差值滤波器模型；

(3) 利用冲击特征比值和二阶原点矩两个特征指标构建形态滤波的复合评价体系；

(4) 依据复合评价体系尺度寻优原则，选择长度和高度尺度组合λ=(λl,λh)；

尺度寻优原则为：①λh=1的条件下，在冲击特征比值K随λl的变化曲线中确定K值最大且数值变化相对稳定的区域，并在该区域内确定二阶原点矩数值最小的λl；② 按确定的λl，在冲击特征比值K随λh的变化曲线中确定K值对应最大的λh。

(5) 利用确定好的λ=(λl,λh)对步骤(1)构建的一维离散时间向量进行多尺度形态滤波处理。

4液压泵故障模拟试验研究

本试验是在材料试验机液压伺服系统试验平台上完成的，试验台如图8所示。以MCY14-1B型号轴向柱塞泵为研究对象，电机额定转速设为1 500 r/min。设置采样频率为50 kHz，并对泵壳的振动信号进行数据采集。人为设计轴向柱塞泵分别在正常状态、单柱塞滑靴磨损和中心弹簧失效三种工作状态下进行试验研究。试验初始压力调定为5 MPa，截取1 s时间段的数据进行分析。在0.4 s时刻设置压力突然上升2倍至10 MPa，并保持0.4 s后迅速下降到5 MPa(模拟持续可变载荷)。

图8　液压泵故障模拟试验台Fig.8 Hydraulic fault simulation test-bed

液压泵各类工作状态的原始信号时域波形如图9所示。从图9可以看出，在0.4～0.8 s时间段随着载荷的突然增大，液压泵振动信号的幅值有明显的提高。但是从时域波形中无法发现表征液压泵各工作状态的显著特征信息。对原始信号进行功率谱分析，如图10所示。从功率谱图中发现特征频率完全被噪声信号所淹没，无法找到反映液压泵各种工作状态的特征频率。

图9　原始信号时域波形Fig.9 Time-domain waveform of original signals

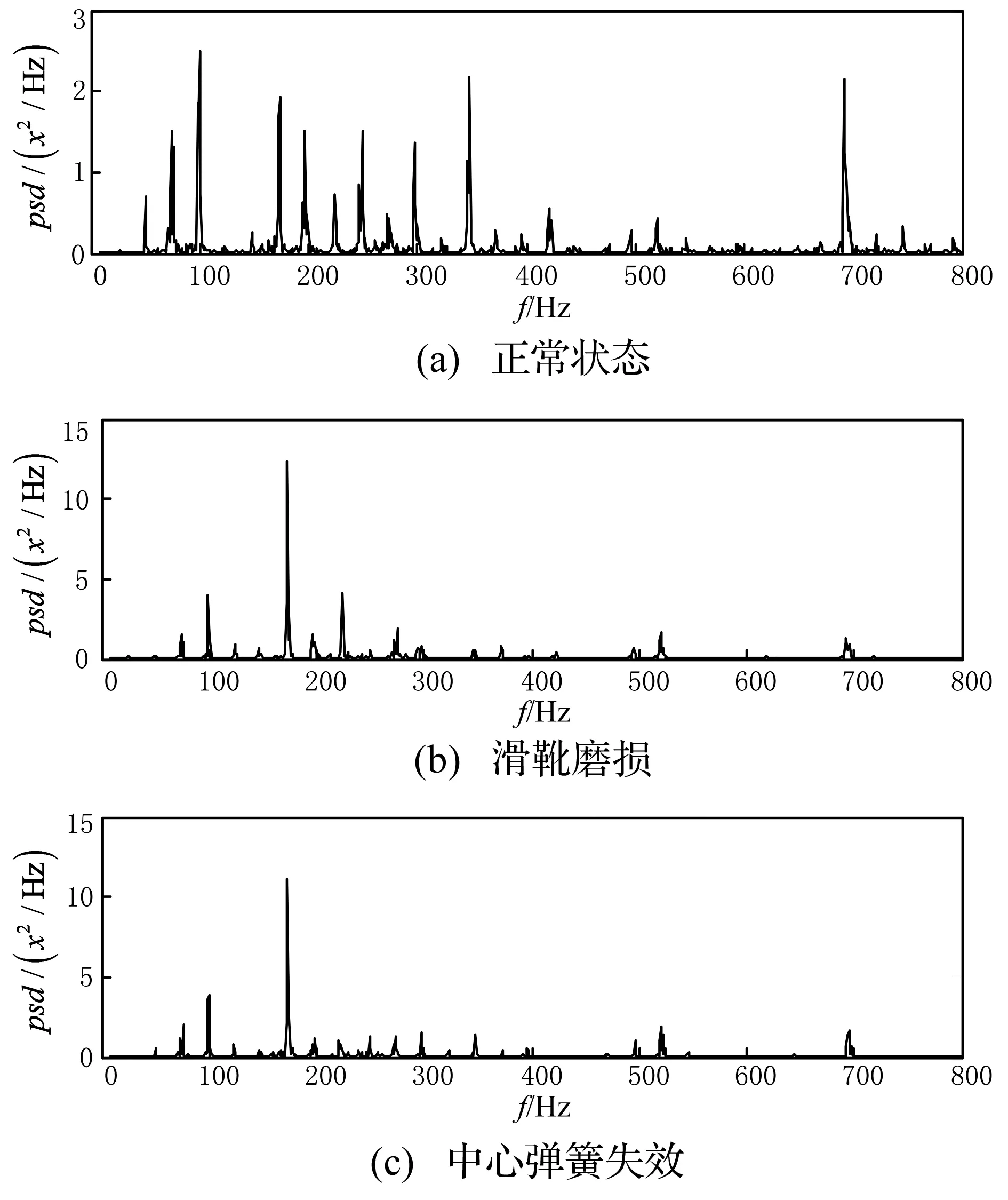
图10　原始信号功率谱Fig.10 Power spectrum of original signals

依据多尺度形态分析方法中复合评价体系的尺度寻优原则和单尺度形态分析方法中最优结构元素长度的选择原则，计算得到正常状态、单柱塞滑靴磨损和中心弹簧失效三种工作状态的尺度，如表1所示。

表1　最优尺度选择

利用形态学分析方法进行滤波得到滤波信号。对滤波信号进行功率谱分析(如图11和图12所示)，可以得出以下结论：

(1) 比较图11(a)和图12(a)可以看出，两种滤波方法得到的泵正常状态下的功率谱差异不大，只是单尺度滤波方法在特征频率175 Hz和350 Hz的能量幅值更大。可以明确地找出轴向柱塞泵滑靴撞击斜盘的冲击振动基频175 Hz和泵的流量脉动频率345 Hz。

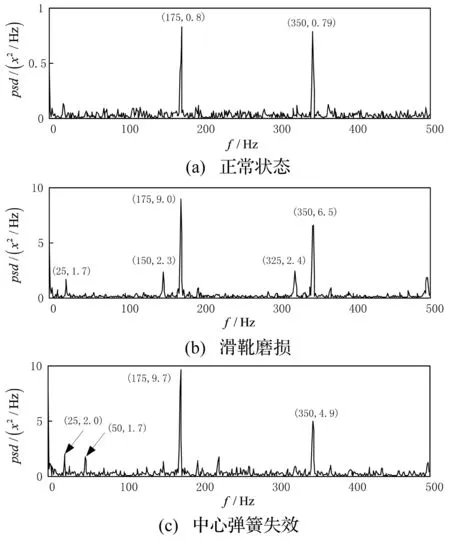
图11　多尺度滤波信号功率谱Fig.11 Power spectrum of multiscale filtered signals

(2) 比较图11(b)和图12(b)可以看出，当单柱塞滑靴磨损故障发生时，单尺度滤波方法得到的功率谱特征频率除175 Hz和350 Hz的能量幅值有所增加外，没有其他特征频率发生变化；而多尺度滤波方法得到的功率谱不仅在175 Hz和350 Hz的能量幅值有明显的增加，而且在25 Hz基频、150 Hz(6倍频)以及325 Hz(13倍频)处出现了明显的能量峰值。根据单柱塞滑靴磨损的故障机理可知，25 Hz基频恰恰是该故障的特征频率，与此同时，通过该滤波方法还找到了反映该故障的另外两个特征频率——150 Hz和325 Hz。

(3) 从对图11(c)和图12(c)的比较来看，当发生中心弹簧故障时，单尺度滤波方法在特征频率上仍然没有表现出明显的故障特征；而多尺度滤波方法得到的功率谱除175 Hz和350 Hz有明显的能量幅值增加外，在25 Hz基频以及50 Hz(2倍频)位置出现了明显的能量峰值。依据中心弹簧失效故障机理可知，25 Hz基频及其2倍频均是该故障的特征频率。

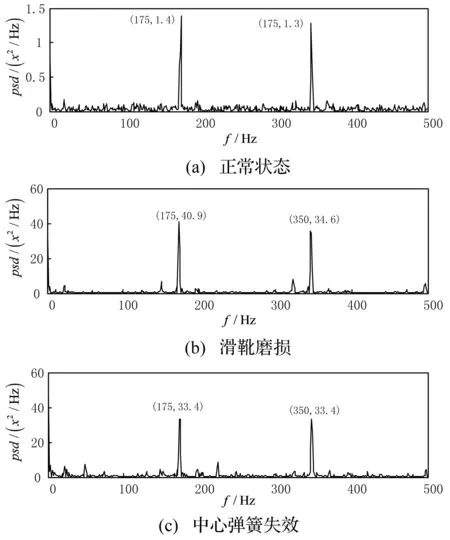
图12　单尺度滤波信号功率谱Fig.12 Power spectrum of single-scale filtered signals

综上所述，单尺度形态滤波方法对持续可变载荷条件下泵不同状态时振动信号表现出的频率特征反映并不明显。而多尺度形态滤波方法则能明显的反映出泵各种状态下的频率特征。由此证明，该条件下多尺度形态滤波方法相比单尺度方法具有更好的滤波效果。

5结论

(1) 多尺度形态滤波方法能根据不同状态的信号进行多尺度寻优，并能解决载荷变化引起泵振动信号幅值变化的问题；

(2) 通过对液压泵多种工作状态的试验研究，利用多尺度形态滤波方法找到了液压泵单柱塞滑靴磨损故障和中心弹簧失效故障对应的特征频率；

(3) 通过试验验证了多尺度形态滤波方法能够对液压泵在持续可变载荷条件下的振动信号进行有效滤波，与单尺度形态滤波方法相比，具有更好的滤波效果。

参 考 文 献

[1] 周汝胜, 焦宗夏, 王少萍. 液压系统故障诊断技术的研究现状与发展趋势[J]. 机械工程学报, 2006, 42(9):6-14.

ZHOU Ru-sheng, JIAO Zong-xia, WANG Shao-ping. Current research and developing trends on fault diagnosis of hydraulic systems[J]. Chinese Journal of Mechanical Engineering, 2006, 42(9):6-14.

[2] 王少萍, 苑中魁, 杨光琴. 基于小波消噪的液压泵故障诊断[J]. 中国机械工程, 2004, 15(13)：1161-1163.

WANG Shao-ping, YUAN Zhong-kui, YANG Guang-qin. Study on fault diagnosis based on wavelet for hydraulic pump[J]. China Mechanical Engineering, 2004, 15(13)：1161-1163.

[3] 姜万录, 张淑清, 王益群. 液压泵故障的小波变换诊断方法[J]. 机械工程学报, 2001, 37(6)：34-37.

JIANG Wan-lu,ZHANG Shu-qing, WANG Yi-qun. Wavelet transform method for fault diagnosis of hydraulic pump[J]. Chinese Journal of Mechanical Engineering, 2001, 37(6)：34-37.

[4] 刘玉娇, 姚恩涛, 徐红专. 基于粒子滤波和自回归谱的液压泵故障诊断[J]. 仪器仪表学报, 2012, 33(3)：561-567.

LIU Yu-jiao, YAO En-tao, XU Hong-zhuan. Fault diagnosis of hydraulic pump based on particle filtering and autoregressive spectrum[J]. Chinese Journal of Scientific Instrument, 2012, 33(3)：561-567.

[5] 李志兴, 谢向荣, 梁述海. 小波包降噪在液压泵故障诊断中的应用[J]. 船海工程, 2006, 35(2)：38-41.

LI Zhi-xing, XIE Xiang-rong, LIANG Shu-hai. The application of wavelet-packet noise reduction for fault diagnose of the hydraulic pump[J]. Ship & Ocean Engineering, 2006, 35(2)：38-41.

[6] 姜万录, 郑直, 朱勇,等. 基于最优扁平型结构元素长度的液压泵故障诊断研究[J]. 振动与冲击, 2014, 33(15)：35-41.

JIANG Wan-lu,ZHENG Zhi, ZHU Yong, et al. Hydraulic pump fault diagnosis based on optimal flat structure element length[J]. Journal of Vibration and Shock, 2014, 33(15)：35-41.

[7] 李扬. 形态学滤波新方法及其在旋转机械故障诊断中的应用[D]. 秦皇岛：燕山大学, 2013.

[8] 章立军, 徐金梧, 阳建宏,等. 自适应多尺度形态学分析及其在轴承故障诊断中的应用[J]. 北京科技大学学报, 2008, 30(4)：441-445.

ZHANG Li-jun, XU Jin-wu, YANG Jian-hong, et al. Adaptive multiscale morphology analysis and its application in fault diagnosis of bearings[J]. Journal of University of Science and Technology Beijing, 2008, 30(4)：441-445.

[9] 郝如江, 卢文秀, 褚福磊. 滚动轴承故障信号的多尺度形态学分析[J]. 机械工程学报, 2008, 44(11)：160-165.

HAO Ru-jiang, LU Wen-xiu, CHU Fu-lei. Multiscale morphological analysis on fault signals of rolling element bearing[J]. Chinese Journal of Mechanical Engineering, 2008, 44(11)：160-165.

[10] Maragos P, Schafer R W. Morphological filters—Part Ⅰ: Their set-theoretic analysis and relations to linear shift-invariant filters[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(8)：1153-1169.

[11] Maragos P, Schafer R W. Morphological filters—Part Ⅱ: Their relations to median, order-statistic, and stack filters[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(8)：1170-1184.

[12] Maragos P. Pattern spectrum and multiscale shape representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7)：701-716.

基金项目：国家重点基础研究发展计划(973计划)资助项目(2014CB046405)；国家自然科学基金资助项目(51505411)；河北省自然科学基金资助项目(E2013203114)

收稿日期：2015-03-16修改稿收到日期：2015-07-03

通信作者王闯 男，硕士生，1991年10月生

中图分类号:TP277

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.028

Multiscale morphological filtering analysis on fault signals of hydraulic pump under continuous variable loads

LIU Si-yuan1,2, WANG Chuang1,2, JIANG Wan-lu1,2, ZHANG Wen-wen2

(1. Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004, China;2.MOE Key Laboratory of Advanced Forging & Stamping Technology and Science, Yanshan University, Qinhuangdao 066004, China)

Abstract:The method of mathematical morphology for single-scale structural elements may not be effective in the filtering analysis on signals of hydraulic pump under variable loads, because the amplitude of vibration signal of hydraulic pump will change with the loads of the hydraulic system, which affect the vibration characteristics of the signal. Based on the method of single-scale morphological analysis, taking into consideration both the length scale(time) and height scale(amplitude), the vibration signals of the pump were analyzed by using a multiscale morphological filter. Taking the impact feature ratio and second geometric moment as characteristic indeces, a composite evaluation system was constructed. And based on that, an optimization method for the length scale and height scale of structural elements was proposed. The fault simulation tests of the hydraulic pump under variable loads were carried out, and the filtering effects of the multiscale morphological analysis algorithm on three different signals, namely, the signals of the hydraulic pump in normal state, single-piston slipper wear and center spring failure, were checked. By comparison with the single-scale morphological filtering method, it indicates that the multiscale morphological filtering method is more suitable to handle the vibration signal under variable loads conditions.

Key words:continuous variable load; multiscale; morphological filtering; hydraulic pump

第一作者 刘思远 男，博士，副教授，1981年6月生