基于塔筒振动特性识别风机塔螺栓松动的研究

何先龙， 佘天莉， 徐　兵， 李　杰， 陈　刚， 曹国福

(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室，哈尔滨　150080；2. 上海勘测设计研究院有限公司，上海　200434)



基于塔筒振动特性识别风机塔螺栓松动的研究

何先龙1， 佘天莉1， 徐兵2， 李杰2， 陈刚2， 曹国福2

(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室，哈尔滨150080；2. 上海勘测设计研究院有限公司，上海200434)

摘要：法兰盘螺栓松动是风机塔常见的一种严重病害。基于大量实测试验得出：塔筒的1阶相位差特性对法兰盘螺栓松动病害很敏感。首先对6座存在此病害的风机塔开展了详细的振动测试与分析，然后分析出法兰盘螺栓松动后，其1阶固有频率值未发生变化、阻尼比变化不明显、1阶振型变化也不突出，但在各法兰盘上、下盘之间的相位差即使在螺栓松动比例为6%时也存在明显的突变特性，而在对法兰盘螺栓重新紧固后，其相位差未表现出此特性。实测试验表明：相比其它振动特性，风机塔的1阶相位差特性受法兰盘螺栓松动的影响更明显，因此能更准确地反映出法兰盘螺栓松动现象，可基于法兰盘上、下盘之间的相位差绝对值是否存在突然增大的特性来识别出法兰盘螺栓是否存在较严重的松动病害。本文的研究结果是基于6座风机塔多个工况下的实测数据得出的，具有较高的可靠性，对风机塔的法兰盘螺栓松动病害的快速检测方法的研究具有较大的参考价值。

关键词：风机塔；法兰盘螺栓松动；塔筒振动特性；相位差特性

最近几年，我国风机倒塌事故屡见不鲜，如2008年吉林某风电场的某台风机使用约3年就完全倒塌；2010年，某风电场的某台风机因为法兰盘上的螺栓未及时紧固而被大风吹倒[1-3]；2014年，甘肃某风机服役未到1年就突然倒塌。

分析上述倒塌事故，可见风机塔法兰盘螺栓松动是导致风机塔倒塌的主要因素，也是风机塔的常见严重病害之一，而导致法兰盘螺栓松动的因素主要有以下几个方面[1,4-6]：① 风机主要运行部件安装存在偏差，导致风机运行时产生的振动较大，导致法兰盘里的螺栓的螺母逐步松动；② 法兰盘里的螺栓没有紧固到位，导致螺母在振动作用下，逐步松动；③ 螺栓材料特性不合格，在振动作用下，螺栓的直径逐步被拉细，导致螺母逐步松动。

因此，尽早发现螺栓的松动情况，有利于预防风机塔倒塌。

现有的方法主要是通过人工逐个螺栓检查法来判断法兰盘里是否出现了较多的螺栓松动现象[1,7-9]。此方法虽然能详细地检查出螺栓松动情况，但是由于每座风机塔的螺栓数量接近百个，如逐个人工检测则既费时也费力。因此对风机塔开展法兰盘螺栓松动的快速识别方法的研究具有较大的工程价值，有利于减少风机塔的维护成本，更有利于促进风机塔运营安全监测技术的发展[10-11]。

风机塔通常由多节塔筒叠加而成，而每节塔筒的底部和顶部都带有法兰盘，且通过大量高性能的螺栓把相邻塔筒的法兰盘连接起来。如果风机塔不存在损伤，其结构动力响应传递函数在线性工作状态下是固定不变的，但是，当法兰螺栓松动时，可等效为螺栓连接构件的刚度折减[6]，导致相邻塔筒之间的相互作用力函数发生变化，进而可能会导致相邻塔筒之间的传递函数发生变化和整座风机塔的传递函数发生变化。因此，理论上如风机塔的螺栓松动比例达到一定程度，会导致风机塔的振动特性发生变化[11]。结构振动模态参数是结构传递函数表达式的重要物理参数，主要有固有频率、振型、阻尼比、相位差、刚度、质量[12-13]。因此，可通过对在役风机塔的结构振动模态参数的测试和计算，分析风机塔动力响应传递函数，特别是相邻塔筒之间的螺栓连接构件的动力响应传递函数是否发生较大变化，进而识别出风机塔的螺栓松动等结构损伤。

本论文对某6座已经存在螺栓松动病害的风机塔分别在对其螺栓重新紧固前后都进行了详细的振动测试，通过实测数据的频谱图发现风机塔的振动能量主要集中在1阶固有频率点，而其它频率点的频谱特性非常不突出。因此本文的研究重点关注塔筒维修前后的1阶模态参数的变化情况，对维修前后的1阶固有频率值、1阶固有频率值对应的阻尼比的变化进行了详细统计，同时以第1个测点顺风向(塔筒最底部测点)的振动信号作为风机塔振动输入信号，分别做出其它测点顺风向相对第1测点顺风向的振动幅频响应归一化曲线和相频响应曲线，然后基于各测点的振动幅频响应归一化曲线得出其1阶固有频率值对应的1阶振型曲线；基于相频响应曲线拾取出1阶固有频率值对应的相频幅值，进而得出其它各测点在1阶固有频率点处相对于第1测点的相位差值，最后以各测点的布置高程为X轴，绘制出风机塔1阶固有频率点对应的振型和相位差曲线。

本次测试通过数据分析，统计出了6座风机塔的1阶固有频率值和1阶固有频率值对应的阻尼比值、振型曲线、相位差曲线在螺栓紧固前后的变化情况，得出1阶固有频率值对应的相位差曲线对法兰螺栓松动病害很敏感的结论。

1风机塔振动测试情况

某陆上风电场位于甘肃金昌市，其大量风机塔存在法兰盘螺栓松动的病害，有的螺栓松动比例超过了50%，特别是某座风机塔因未急时发现此病害，在使用不到1年就倒塌了。

螺栓完全拧紧是指采用扭矩法或转角法拧紧螺栓(螺母)时，拧紧螺栓(螺母)的装配的扭矩达到上限时(扭矩上限值主要依据螺栓和螺母的材料屈服强度值设定，通常取屈服强度对应的扭矩的70%)，螺栓(螺母)不再产生位移(转角)；而螺栓松动现象是指当采用扭矩法或转角法拧紧螺母时，拧紧螺栓(螺母的装配的扭矩在低于上限时，螺栓(螺母)仍旧存在位移(转角)[14]。因此，可通过扭矩法或转角法可检测出螺栓(螺母)是否松动和基于最开始的拧紧扭矩值定量螺栓(螺母)的松动程度。本次实验由于在重新拧紧螺栓(螺母)时，实验计划不完善和现场工作量的巨大，因此只记录了存在松动现象的螺栓(螺母)的数量，而没有记录拧紧初始扭矩值。

振动是引起螺栓松动的主要因素之一，反之螺栓松动也会引起风机塔振动特性的变化。因此，本次实验选择了此风电场里存在不同程度螺栓松动情况的六座风机塔进行详细的振动测试，研究螺栓松动对风机塔振动特性的影响情况。六座风机塔的基本情况和螺栓松动比例见表1，其中1号和2号风机塔为1.5兆瓦机组，3～6号风机塔为2兆瓦机组，塔筒法兰盘上的螺栓规格为M36*480的10.9级高强度螺栓，其特性检测结果符合GB/T 3098.1—2010《紧固件机械性能螺栓、螺钉和螺柱》标准要求。

在各风机塔筒壁上由低到高布置12个测点，每个测点布置1台由北京腾晟桥康科技有限公司生产的QZ2013型单分量力平衡加速度计，沿主风向(西北向)布置，具体布置情况见表2。此加速度计频带范围为0～200 Hz,具有良好的微振和强振拾取能力。数据采集仪采用由北京腾晟桥康科技有限公司生产的G01NET-2型同步动态数据采集仪，其AD位数为24位。

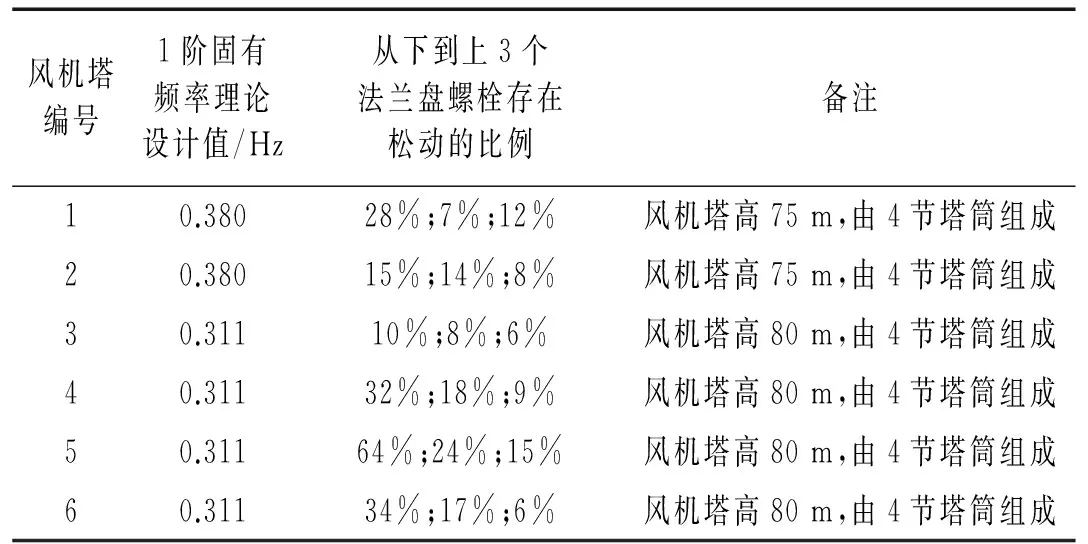
表1　6座风机塔的螺栓松动比例统计

注：螺栓松动比例是指单对上、下法兰盘之间的螺栓(螺母)存在松动现象的数量除以此法兰螺栓(螺母)总数的百分比。

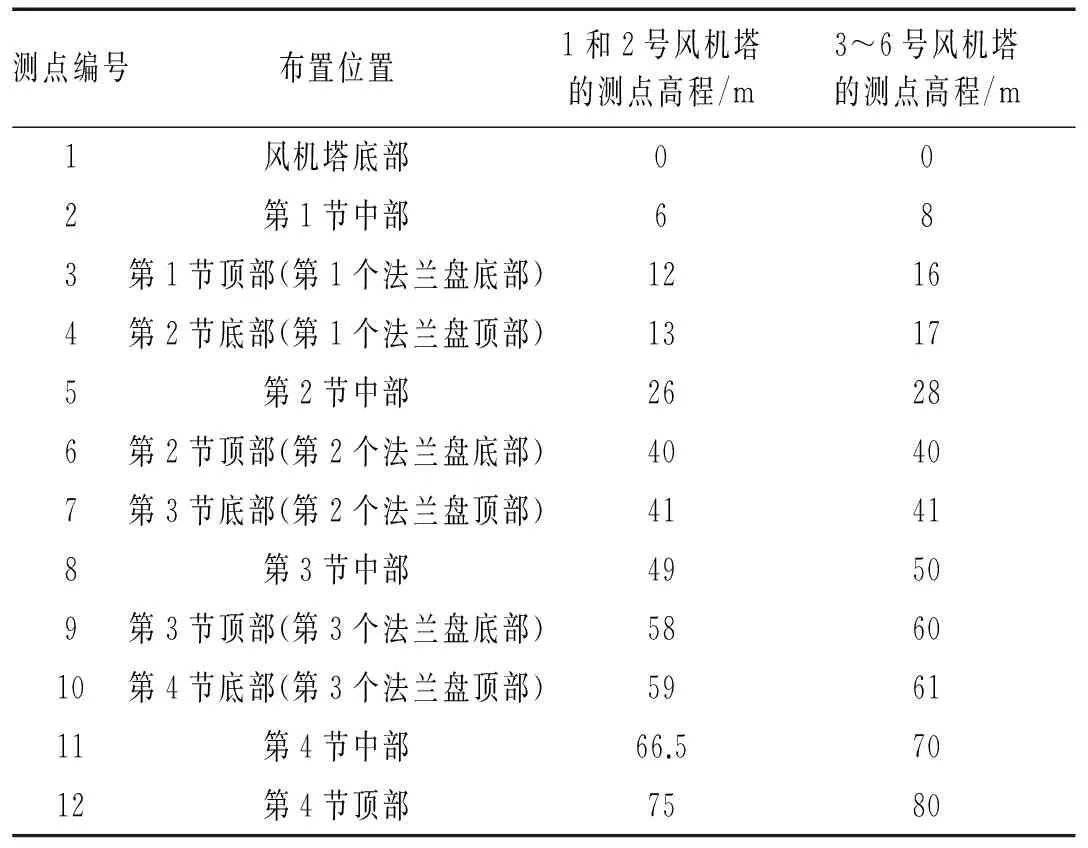
表2　各风机塔主风向水平振动测点布置说明表

为了研究风机塔振动特性对风机塔法兰盘松动程度的敏感程度，我们对各风机塔实施了如表3所示的测试工况。测试时采样频率统一为64 Hz，每个工况连续记录20分钟的数据，所测得的风机塔振动典型波形如图1和2所示。

2风机塔振动特性分析

2.1固有频率与阻尼比分析

对各工况下采集到的振动数据进行FFT平均频谱分析(平均窗为81 920×64，频率分辨率为0.000 78 Hz)，得到风机塔的固有频率值；同时基于半功率谱细化法计算出固有频率点的阻尼比，其功率谱如图3所示。由其功率谱可见风机塔的振动能量主要集中在1阶固有频率点，其它的固有频率非常不突出。表4和表5分别为各风机塔的1阶固有频率与阻尼比分析结果统计情况。

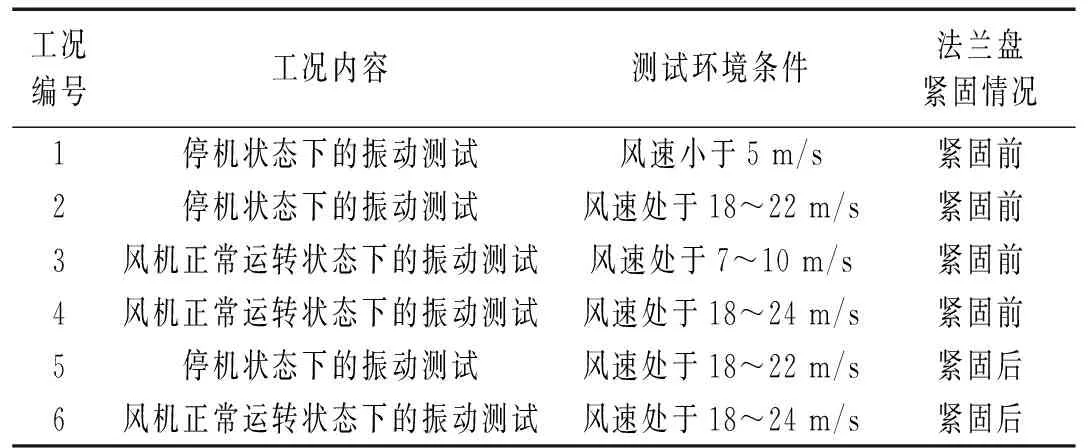
表3　 风机塔振动测试工况

注：法兰盘紧固是只对法兰盘上的各螺栓采用扭矩法进行重新紧固

图1　在7～10 m/s风速时某风机塔工作状态下的塔顶振动加速度时程曲线Fig.1 The acceleration time-amplitude map of a working top-tower in (7～10) m/s winds

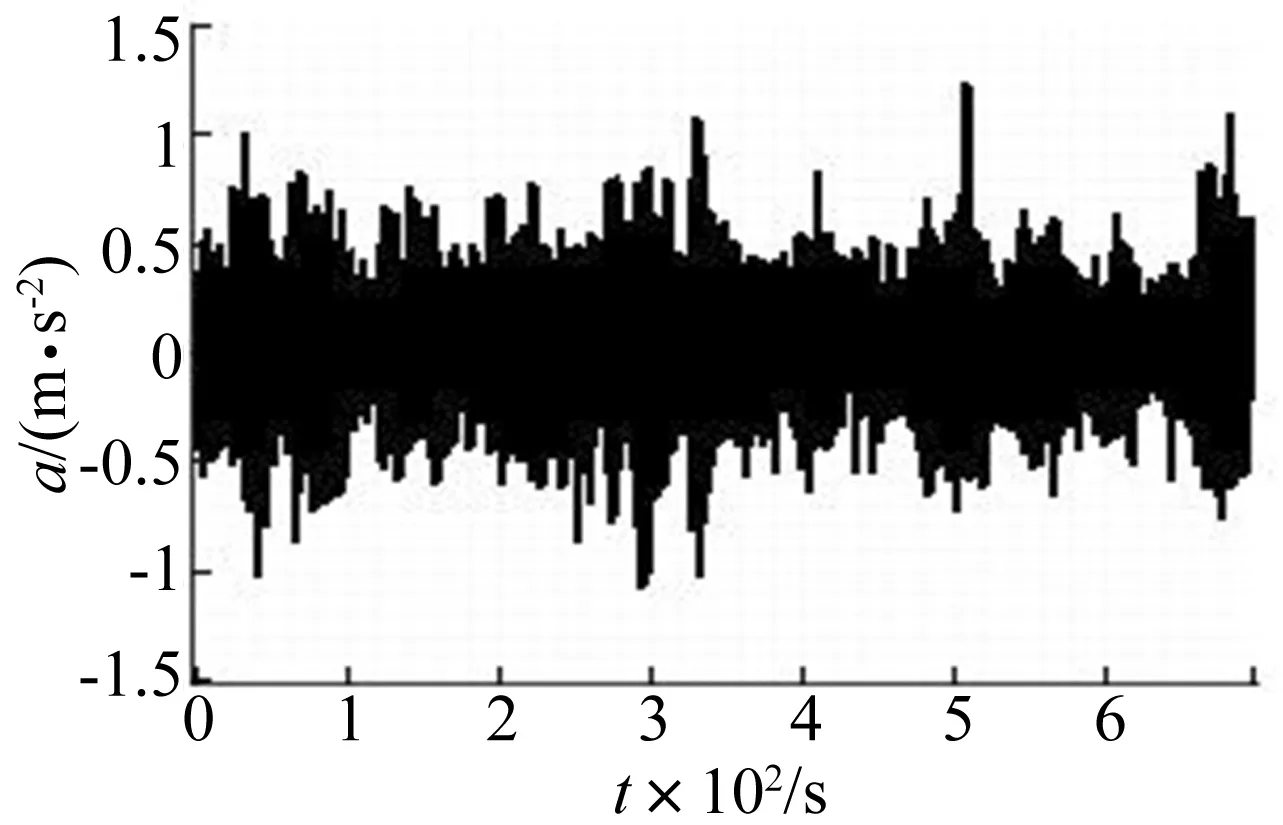
图2　在18～24 m/s风速时某风机塔工作状态下的塔顶振动加速度时程曲线Fig.2 The acceleration time-amplitude map of a working top-tower in (8～24) m/s winds

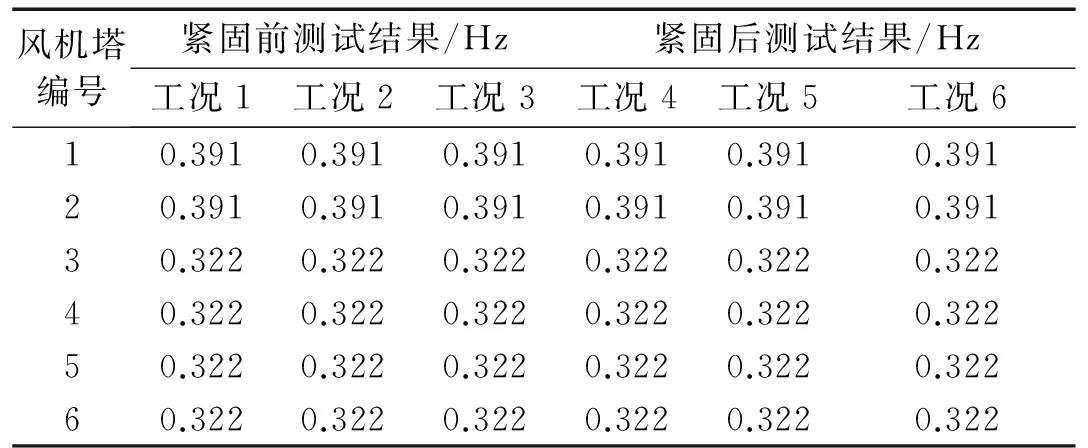
风机塔编号紧固前测试结果/Hz紧固后测试结果/Hz工况1工况2工况3工况4工况5工况610.3910.3910.3910.3910.3910.39120.3910.3910.3910.3910.3910.39130.3220.3220.3220.3220.3220.32240.3220.3220.3220.3220.3220.32250.3220.3220.3220.3220.3220.32260.3220.3220.3220.3220.3220.322

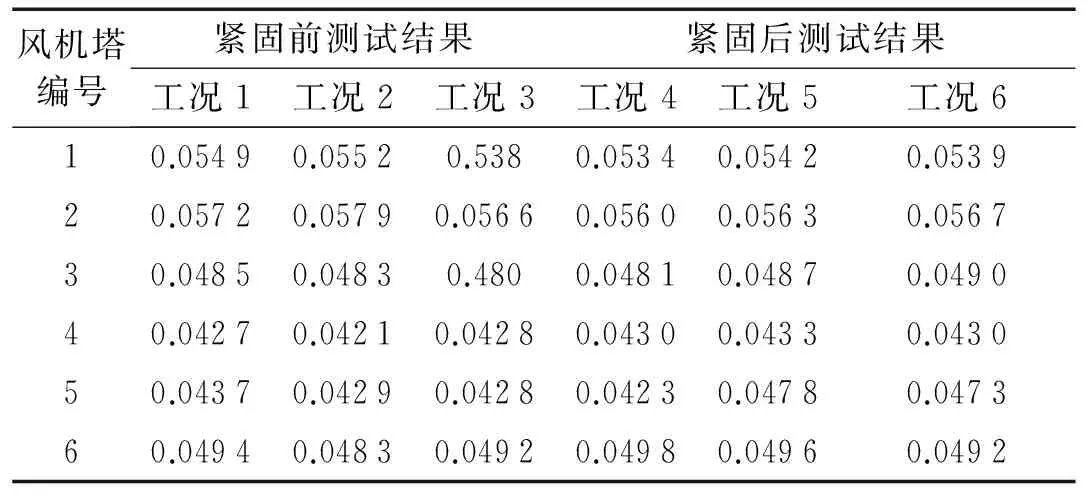
表5　风机塔1阶固有频率点对应的阻尼比分析结果

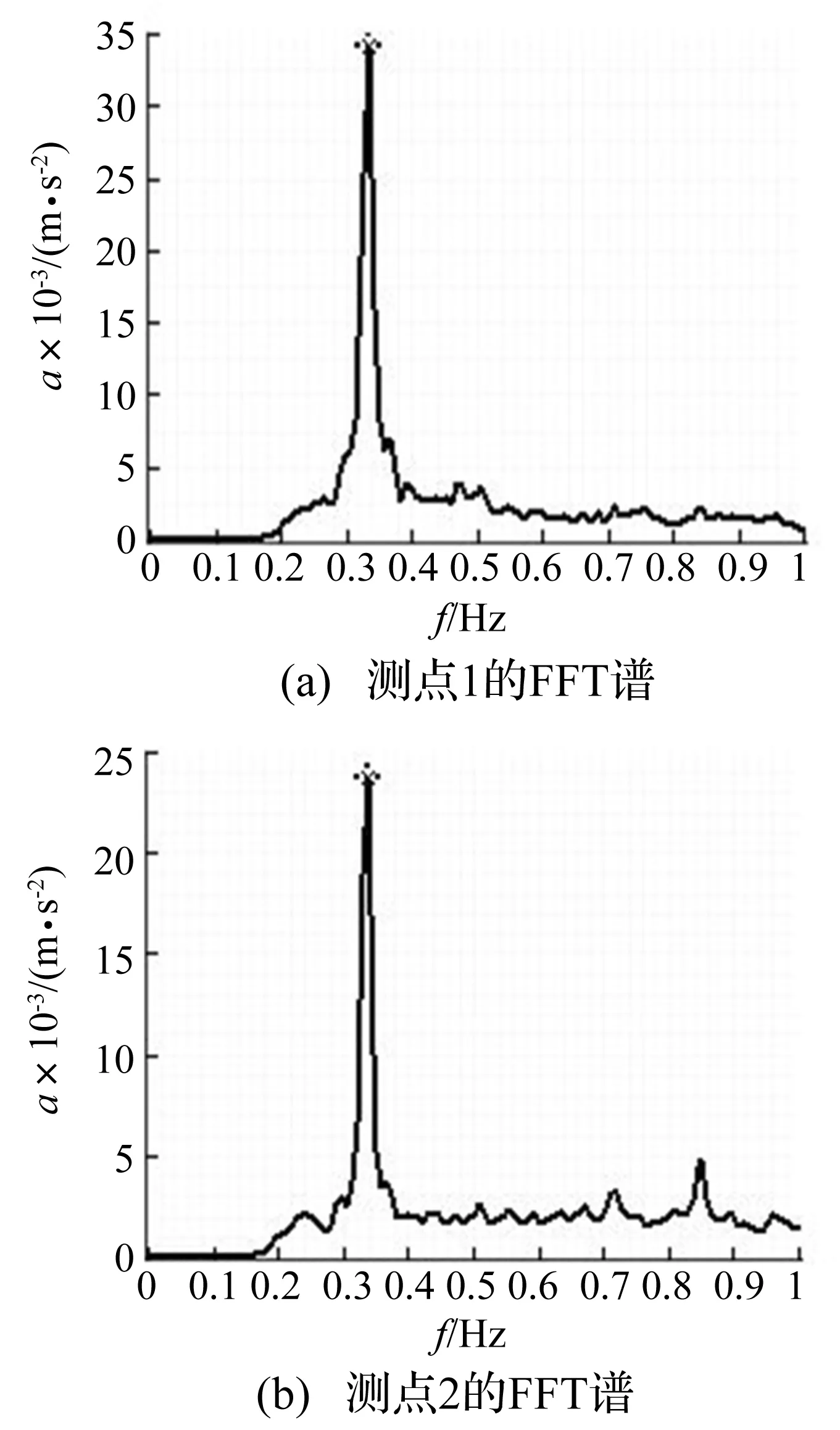
图3某座风机塔实测振动FFT谱图Fig.3 The vibration FFT spectrum of a wind turbine tower

由图3可见，风机塔的主要振动能量集中在塔筒的1阶固有频率点处，其它固有频率点非常不突出。因此，风机塔的振动属于超低频振动，这也表明了风机塔是一种非常柔性的高层建筑物。

由表4可知，各风机塔的1阶振动固有频率值在法兰盘紧固前后的值完全一样，且在停机、正常运转下所测得的1阶固有频率值也完全一样。这说明了法兰盘的螺栓松动的松动比例虽然比较高，例如5号风机塔的第1个法兰盘上螺栓存在松动的比例松高达64%，但是螺栓重新紧固后的1阶固有频率值仍旧与紧固前的值完全一样。因此，通过分析6座风机塔的振动频谱表面塔筒的振动能量虽然主要集中在1阶固有频率值处，但1阶固有频率值的变化对风机塔法兰盘螺栓松动病害很不敏感。

由表5可知，各风机塔的1阶固有频率值对应的阻尼比值在螺栓紧固前后所测得的值变化非常小，其中1、2、3、4、6号风机塔的阻尼比值变化幅度都小于3%，5号风机塔的第1个法兰盘螺栓松动比例虽然达到了63%，但是其阻尼比值也只是变化了10%左右。因此，通过6座风机塔振动测试表面塔筒的1阶固有频率值对应的阻尼比值对风机塔法兰盘螺栓松动病害的不是很敏感。

2.2风机塔1阶振型与相位差分析

对6座风机塔在各工况下所测得的塔筒1阶振型和1阶相位差曲线进行了详细分析，各风机塔的1阶振型和1阶相位差曲线如图4～图9所示。

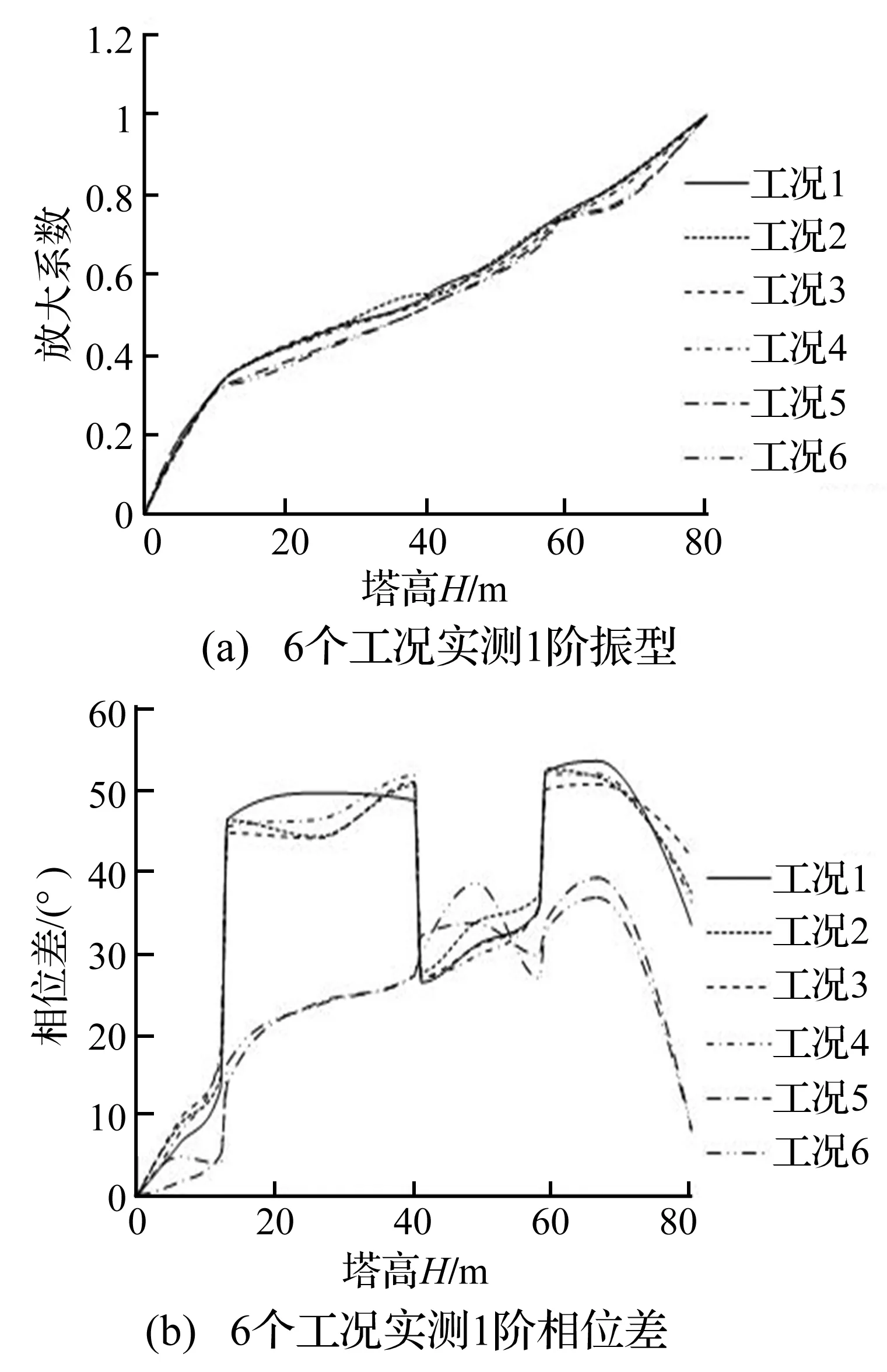
图4　1号风机塔的振型与相位差曲线Fig.4 The vibration mode and the phase difference of No.1 tower

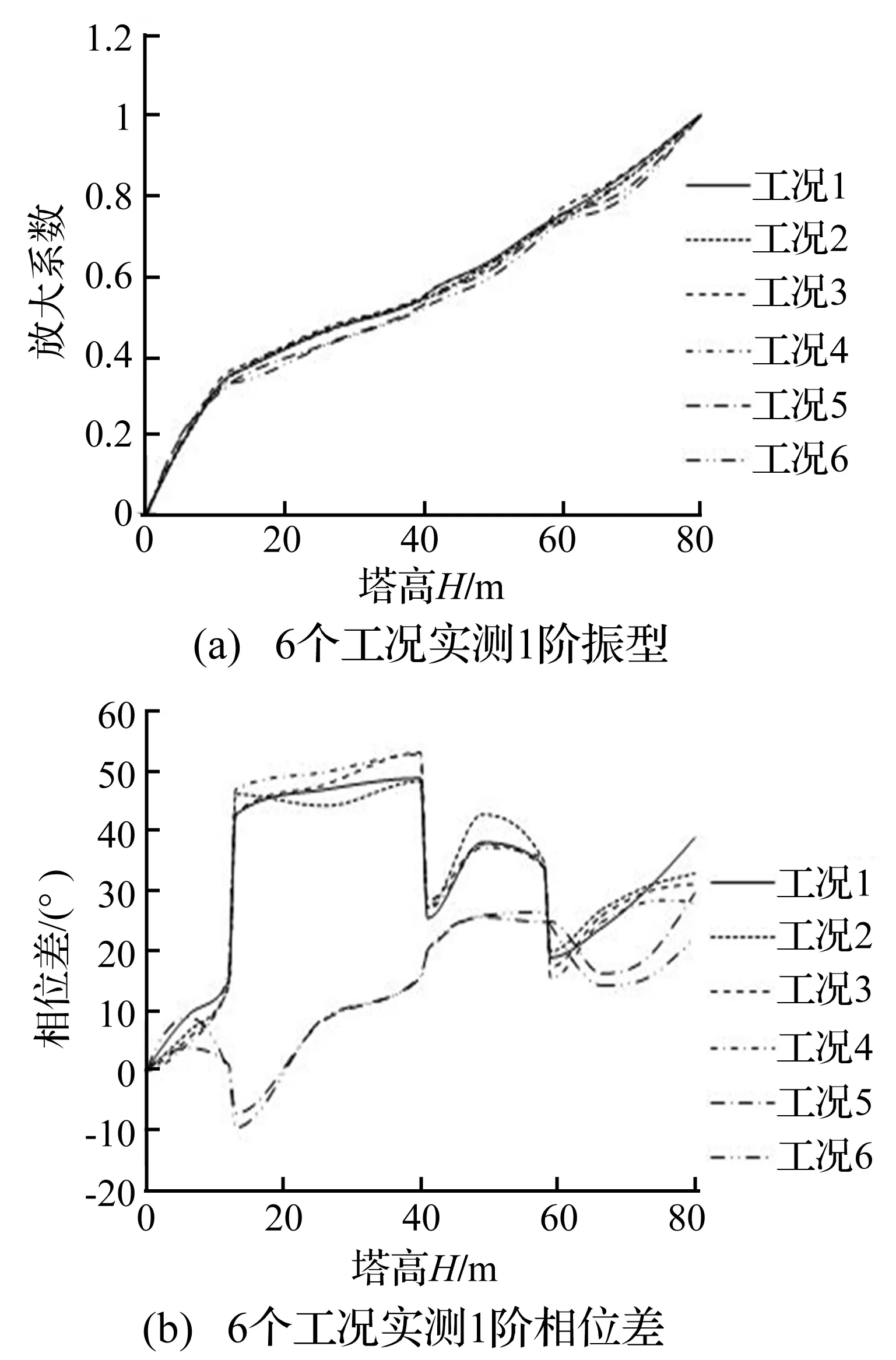
图5　2号风机塔的振型与相位差曲线Fig.5 The vibration mode and the phase difference of No.2 tower

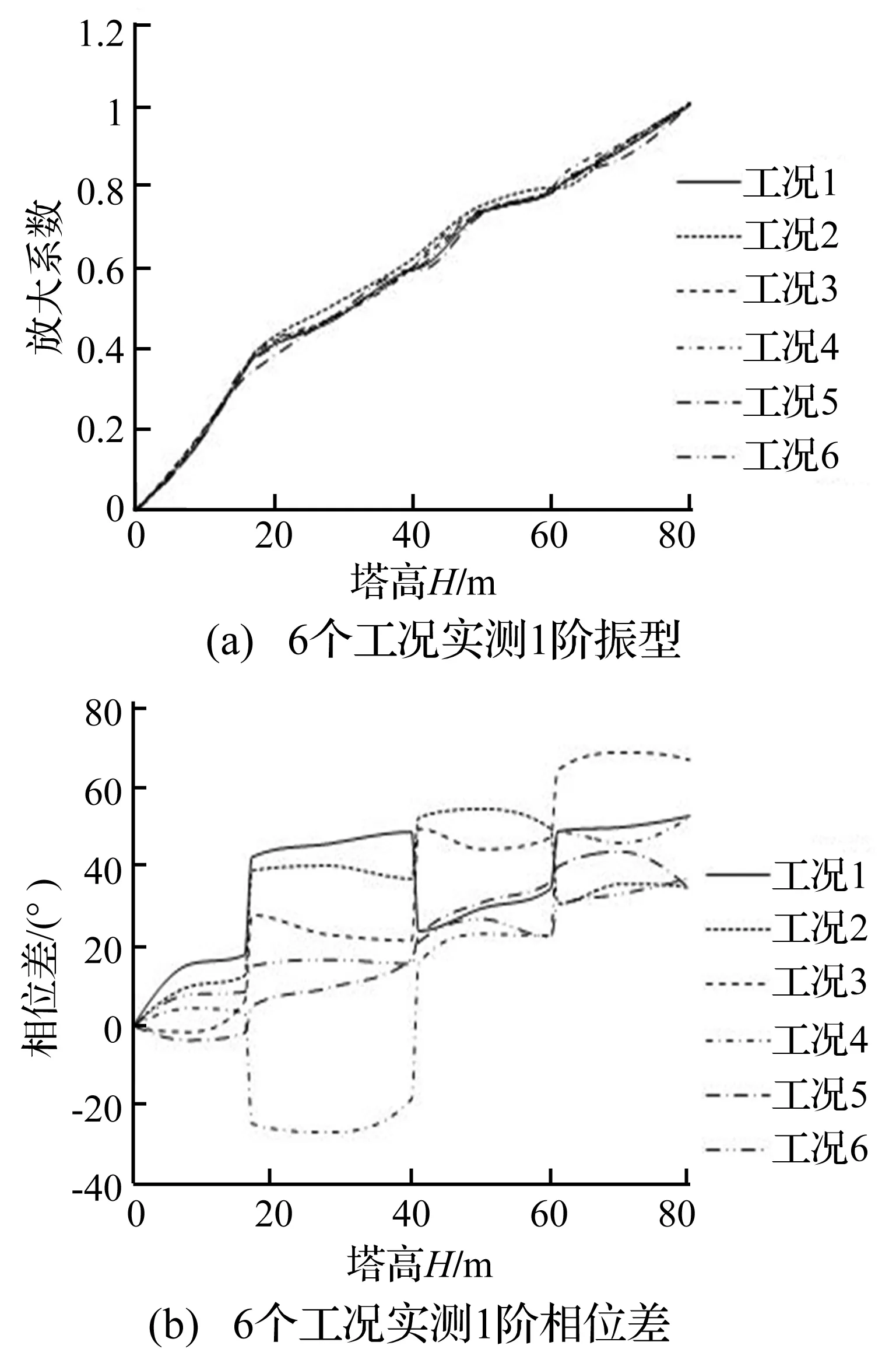
图6　3号风机塔的振型与相位差曲线Fig.6 The vibration mode and the phase difference of No.3 tower

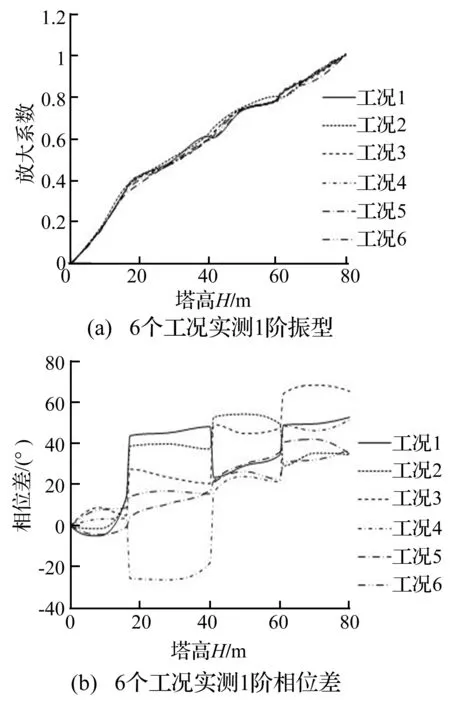
图7　4号风机塔的振型与相位差曲线Fig.7 The vibration mode and the phase difference of No.4 tower

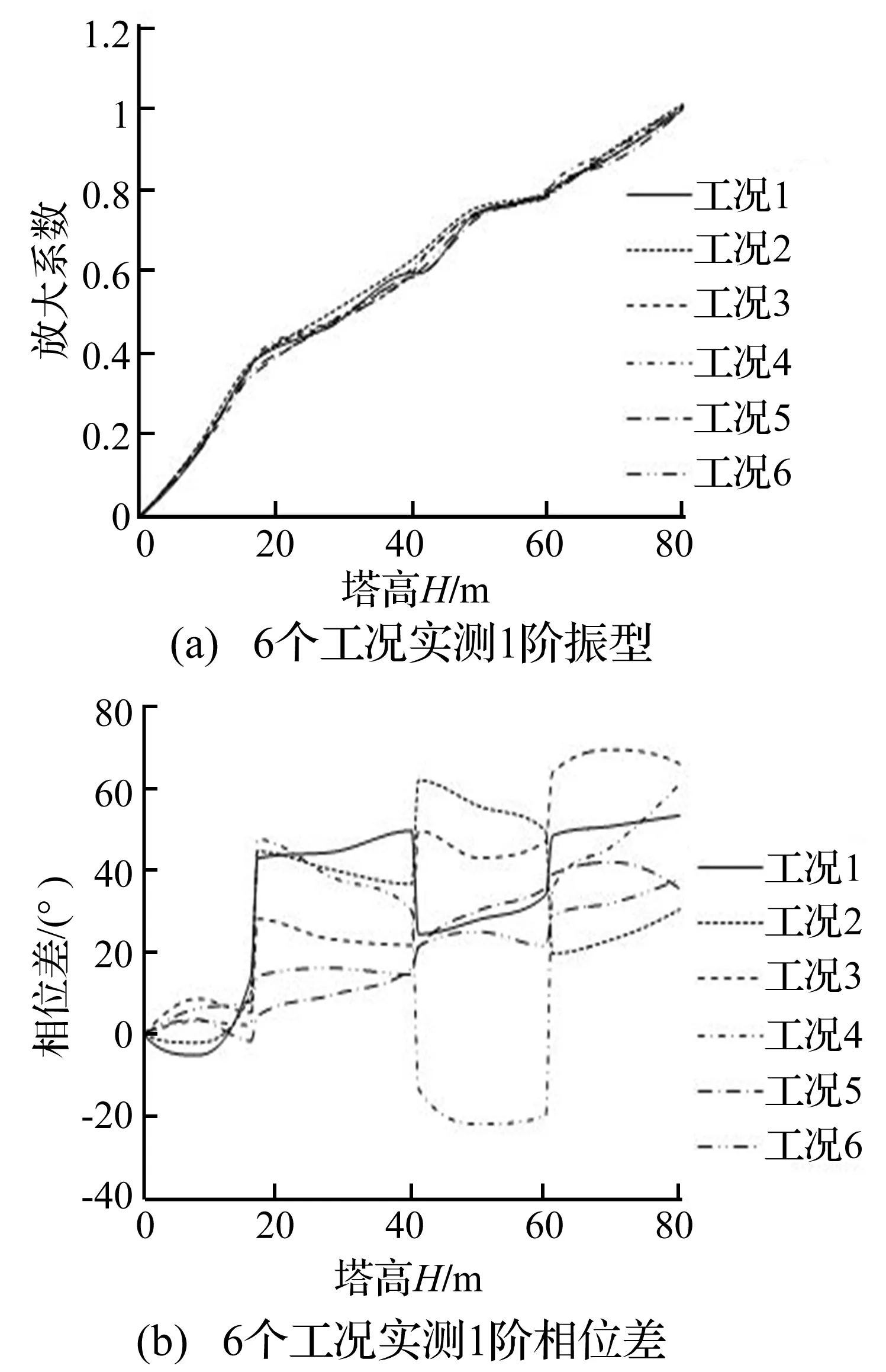
图8　5号风机塔的振型与相位差曲线Fig.8 The vibration mode and the phase difference of No.5 tower

由图4～图9可见，6座风机塔在各工况下所测得的风机塔1阶振型变化不大，在螺栓重新紧固前的1阶振型与重新紧固后的1阶振型比较，非常相似。因此通过分析6座风机塔在螺栓重新紧固前后的1阶振型，表面塔筒的1阶振型对法兰盘螺栓的松动不敏感。

由图2～图7可见，6座风机塔在各工况下所测得的风机塔1阶相位差曲线变化都比较大。在螺栓重新紧固前，1～4工况下所测得的相位差曲线在上螺栓的法兰盘处存在突变现象，即法兰盘下盘与上盘两个测点之间虽然相距1米高程，但相对其它高层，相位差明显增大或明显减小，且每座风机塔的3个法兰盘上下盘附近测点之间相位差都表现出了此特点，如3号风机塔的第3个法兰盘螺栓松动比例虽然才6%，但是其上、下盘附近测点之间也明显地出现了突变现象。在螺栓重新紧固后，5～6工况下所测得的相位差曲线相比螺栓重新紧固前的相位差曲线，变化比较平稳，特别是在上螺栓的法兰盘的上、下盘附近测点之间未出现明显增大或减小的现象。因此通过分析6座风机塔在螺栓重新紧固前后的1阶相位差曲线，表明在法兰盘螺栓松动比例即使较低时，如6%时，也会引起法兰盘的上、下盘之间的相位差出现明显变化。这充分地表明了塔筒的1阶相位差曲线对法兰盘螺栓的松动是非常敏感的。

6座风机塔法兰盘都存在不同程度的松动，通过对比它们的法兰盘螺栓重新紧固前后的振动特性分析得出它们的固有频率、阻尼比、1阶振型、1阶相位差的变化特性见表6。

表6　6座风机塔螺栓紧固前后的振动特性统计

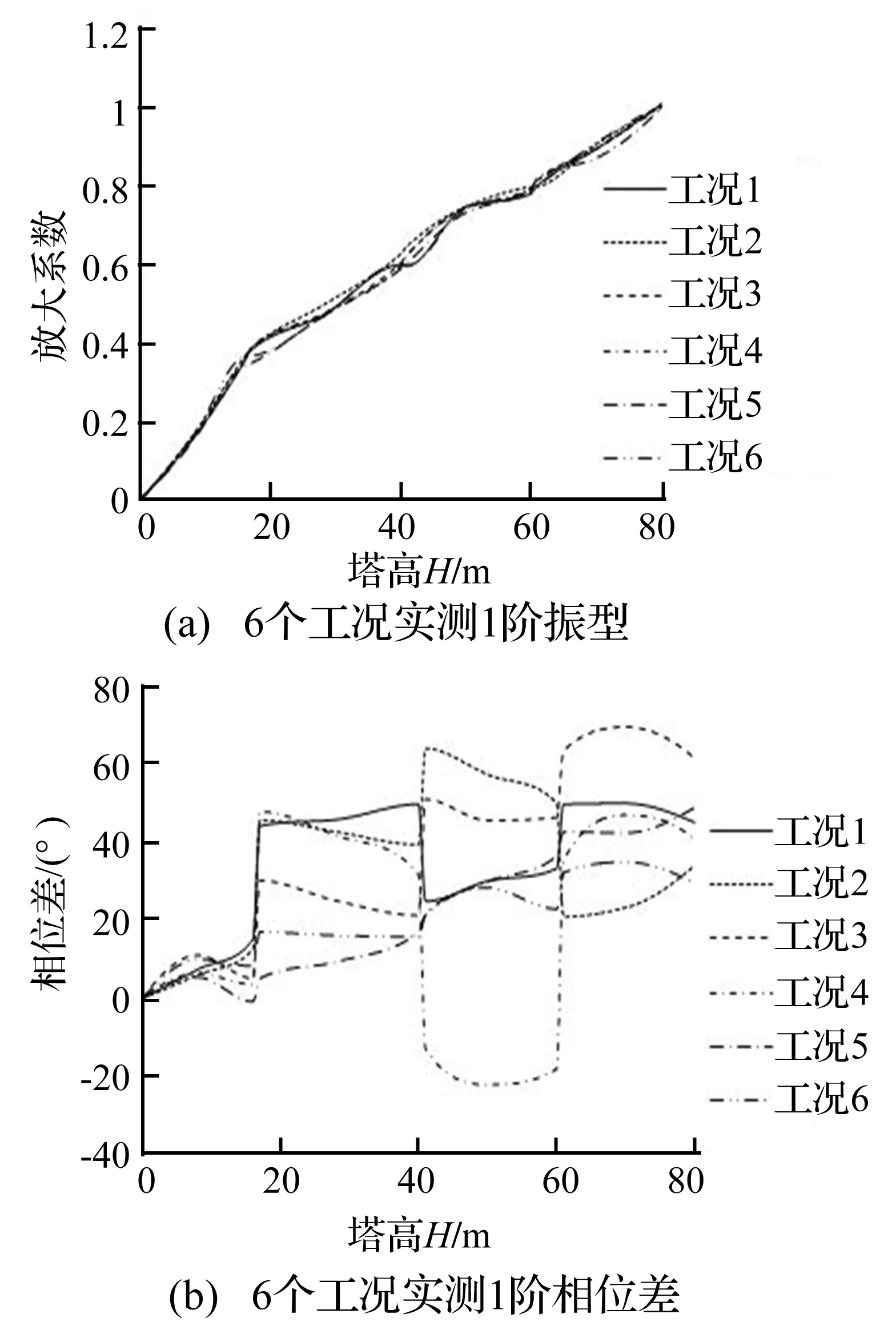
图9　6号风机塔的振型与相位差曲线Fig.9 The vibration mode and the phase difference of No.6 tower

3结论

螺栓是风机塔的重要构件，用于连接各节塔筒，但是由于长期处于较大的振动环境，很容易出现松动现象，严重时直接导致风机塔倒塌。因此，连接法兰盘的螺栓松动现象是风机塔的常见严重病害之一，也是风机塔日常维护的主要对象。本文通过对6座存在此病害的风机塔在维修前后都开展了详细的振动测试与分析，得出风机塔的振动特性与风机塔螺栓松动之间存在以下关系：

(1) 风机塔的1阶固有频率一般低于0.5 Hz，且主要振动能量集中于此频率点，但是对风机塔法兰盘螺栓松动很不敏感，如某法兰盘螺栓松动比例虽然达到了64%，但是1阶固有频率值与螺栓重新紧固后所测得的值完全相同。

(2) 风机塔的1阶固有频率对应的阻尼比值在法兰盘螺栓重新紧固前后出现了变化，但是变化较小，如5号风机塔第1个法兰盘螺栓虽然松动比例达到了64%，且另外两个法兰盘上的螺栓松动比例也分别高达24%和15%，但是相比螺栓重新紧固后的阻尼比值，变化也才10%。

(3) 与螺栓重新紧固后的1阶振型曲线相比，6座风机塔的螺栓虽然存在较高比例的松动，但是1阶振型曲线变化不大。

(4) 螺栓存在一定比例松动的法兰盘在其上、下盘之间的相位差绝对值相比螺栓重新紧固后的相位差绝对值会明显增大，如某法兰盘螺栓松动比例虽然才6%，但是其上、下盘之间的相位差绝对值也明显增大了。

综合以上所述表明：风机塔的固有频率、阻尼比、振型等振动特性对法兰盘螺栓松动病害不敏感，但是风机塔法兰盘上、下盘的相位差绝对值对法兰盘螺栓松动病害非常敏感，可基于风机塔的振动特性-相位差的变化特性识别法兰盘螺栓的松动情况。因此本文对6座存在螺栓松动病害的风机塔进行了详细的振动测试，测试数据的分析结果在风机塔法兰盘螺栓松动快速检测及运营安全的实时监测方面的研究具有一定的借鉴价值。

参 考 文 献

[1] 魏泰，吴坤，黄军威. 风机塔筒螺栓防松检测技术[J]. 机械与电子，2013(8)：78-80.

WEI Tai, WU Kun, HUANG Jun-wei. Prevent loosing detection technology of the wind turbines tower bolts [J]. Machinery & Electronics, 2013(8)：78-80.

[2] 李本立, 宋宪耕. 风力机结构动力学[M]. 北京：北京航空航天大学出版社, 1999.

[3] 龚元明，吴长水．高强度螺栓试验与测试系统的开发[J]．上海工程技术大学学报，2011,25(1)：27-30.

GONG Yuan-ming, WU Chang-shui. Development of testing and measuring system for high strength bolt [J]. Journal of Shanghai University of Engineering Science, 2011,25(1)：27-30.

[4] 缑百勇，陆秋海，王波,等. 利用固有频率异常值分析法检测螺栓拧紧力[J]. 振动与冲击，2015,34 (23): 77-82.

GOU Bai-yong, LU Qiu-hai, WANG Bo, et al. Bolt tightening force detection using outlier analysis of structural natural frequencies [J]. Journal of Vibration and Shock, 2015,34 (23): 77-82.

[5] 余坚，谢寿生，任立通,等.拉杆转子装配振动检测分形研究[J]. 振动与冲击，2014,33(14): 84-88.

YU Jian, XIE Shou-sheng, REN Li-tong, et al. Fractal research on the assembly vibration detection of rod fastening rotor [J]. Journal of Vibration and Shock, 2014,33(14): 84-88.

[6] 李允公，孔祥娜，高玉勇. 基于两被联件振动信号概率密度和PCA的螺栓松动识别方法研究[J]. 振动与冲击，2015,34 (1): 63-67.

LI Yun-gong, KONG Xiang-na，GAO Yu-yong. Method for detecting bolt looseness based on probability density of vibration signals of two connected parts and principal component analysis [J]. Journal of Vibration and Shock, 2015,34 (1): 63-67.

[7] 李源，曾宇，陈昌林. 不同单元类型风机塔筒振动特性比较研究[J]. 东方电机，2012(5):43-46.

YI Yuan, ZENG Yu, CHEN Chang-lin. Comparison with the vibration characteristics of the different wind turbine towers [J]. Dongfang Electrical Machine, 2012(5):43-46.

[8] Rachid Y, Ismail E B, Tritsch J B, et al. Dynamic study of a wind turbine blade with horizontal axis [J]. European Journal of Mechanics-A/Solids,2001, 20(2)：216-225.

[9] Murtagh P J, Basu B, Broderick B M. Mode acceleration approach for rotating wind turbine blades[J].Journal of Multi-Body Dynamics,2001, 21(8)：241-252.

[10] Murtagh P J，Basu B，Broderick B M．Along-wind response of a wind turbine tower with blade coupling subjected to rotationally sampled wind loading [J]．Engineering Structures，2005，27(8)：1209-1219.

[11] 刘贻雄. 大型风力机塔筒结构动力学与稳定性分析[D]. 兰州:兰州理工大学, 2012.

[12] Ren Wei-xin,Roeck G D. Structural damage identification using modal data. I: Simulation verification[J]. Journal of Structural Engineering,ASCE,2002,128(1): 87-95.

[13] Ren Wei-xin,Roeck G D. Structural damage identification using modal data.Ⅱ: Test verification[J]. Journal of Structural Engineering,ASCE,2002, 128(1): 96-104.

[14] 朱正德，林湖. 基于螺栓装配技术中扭矩法与扭矩转角法比较与应用的研究[J]. 柴油机设计与制造学报，2005, 2(14)：39-42.

ZHU Zheng-de,LIN Hu. The research of torque method and torgue/rotation method[J]. Design & Manufacture of Diesel Engine,2005, 2(14)：39-42.

基金项目：国家自然青年科学基金(51508536)；上海市科学技术科研项目(14DZ1200904)

收稿日期：2015-12-03修改稿收到日期：2016-02-23

通信作者佘天莉 女，博士，助研，1971年10月生

中图分类号:TK83；O329

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.018

Method for detecting bolts looseness of a wind turbine tower based on its vibration characteristics

HE Xian-long1, SHE Tian-li1, XU Bing2, LI Jie2, CHEN Gang2, CAO Guo-fu2

(1. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China；2. Shanghai Investigation, Design and Research Institute Co., Ltd., Shanghai 200434, China)

Abstract:The bolt looseness is a usual and serious disease of wind turbine towers. Based on a large number of measurements, the conclusion was obtained that the first-order phase difference characteristic of a wind turbine tower is sensitive to the loosen bolts of its flanges. Six wind turbine towers with loosen bolts were measured and analyzed for their vibration parameters. After the bolts looseness, the first-order natural frequency keeps unchanged and the variations in its damping ratio and its first-order vibration mode are also not obvious. At the same time, there appears an obvious sudden change in the phase difference of the upper and lower flanges despite the bolts looseness ratio reaches 6%. But the phase difference of the upper and lower flanges doesn’t show the sudden change once again after their re-fastening. The measurements show that the first-order phase difference characteristic of a wind turbine tower is more affected by its loosen bolts of flanges than other vibration characteristics. As a result, the first-order phase difference characteristic can express the bolts looseness of flanges more accurately. The serious bolts looseness can be detected by the sudden increasing of the absolute values of the phase difference of upper and lower flanges. Based on the field measurements of six wind turbine towers under different working conditions, the method presented is more reliable and more effective to detect the loosen bolts of wind turbine towers rapidly.

Key words:wind turbine tower; loosen bolt of flange; vibration characteristics of tower; characteristic of phase difference

第一作者 何先龙 男，博士，助研，1981年6月生