爆炸冲击下车辆底部结构与座椅系统多参数优化研究

魏　然, 王显会, 周云波, 张　明, 王良模

(南京理工大学 机械工程学院，南京　210094)



爆炸冲击下车辆底部结构与座椅系统多参数优化研究

魏然, 王显会, 周云波, 张明, 王良模

(南京理工大学 机械工程学院，南京210094)

摘要：为了减少爆炸冲击环境下某防护型车辆内的乘员损伤，对车辆底部结构与座椅系统进行多参数优化。优化过程中，利用多物质单元与流-固耦合算法仿真乘员损伤，并通过试验标定。以乘员小腿受力、颈部力矩为目标函数，以车辆底部结构的厚度、材料、座椅安装位置为设计参数，建立了底部结构及座椅系统的优化数学模型。引入多元统计学的降维技术，形成了基于因子分析的多参数优化方法，在满足精度的条件下，合理缩减参数样本空间，节省了计算成本。通过该算法得到了优化模型的帕累托解集，最终获得了减小乘员损伤的底部结构与座椅系统设计方案。

关键词：车辆底部构型；抗爆炸冲击；多参数优化；因子分析；乘员损伤

车辆及车内乘员在作战、维和任务中的地面威胁主要来自地雷和简易爆炸物的袭击[1]，车辆底部结构与座椅系统(简称底部系统，UCSS)直接影响车内乘员的生还率。为了提升车辆底部防护能力，国内外多采用有限元仿真对底部构型进行辅助设计，结合多物质单元算法(ALE)与流-固耦合算法[2-3](FSI)能精确模拟爆炸冲击波作用下的结构及乘员响应，Fatt等[4]和李利莎等[5]分别模拟了三明治结构和复合结构在冲击作用下的变形和响应，仿真与试验结果有较高的吻合度。但该算法需要计算车辆底部的爆炸冲击波流场，在全尺寸的车辆仿真中，模型单元总数超过百万，针对大规模仿真优化问题，国内外目前已形成了基于实验设计、响应面法[6]的多参数优化方法(MO)，其优化精度较高，但占用较多的计算资源，为进一步缩减计算成本，工程中常通过参数筛选[7-8](如灵明度、贡献度分析等)，牺牲一定的优化精度，去掉“不重要”的设计参数，减少实验设计中的仿真样本量。基于参数筛选的多参数优化(PSMO)往往忽略了参数间的交互效应，随着参数维度增加，参数的筛选将影响优化精度。

本文结合FSI与ALE仿真算法对爆炸冲击下的底部系统进行辅助设计与优化，为了节省计算成本，保证优化精度，引入多元统计中的降维技术，形成基于因子分析的多参数优化(FAMO)，并探讨不同优化算法所获得的底部系统设计方案的差异。

1因子分析多参数优化

1.1因子分析理论

因子分析是研究如何以最少的信息丢失，将众多原始参数缩减成少数几个因子变量，以及如何使因子变量具有较强的可解释性的一种多元统计分析方法。进行因子分析前通常需要进行KMO检验和Barlett检验，一般的，当KMO>0.8或Bartlett伴随概率Sig.<0.05时，设计参数适合进行因子分析。因子分析的基本数学模型为：

X=AF+ε

(1)

式中：X=(X1,X2…Xp)T为设计参数；ε为误差因子，满足正态分布。A为载荷矩阵，F=(F1,F2…Fm)T为相互独立的因子变量，其回归解法为：

F=A′C-1X=WX

(2)

式中：W为得分系数矩阵，利用式(1)、(2)，建立设计变量与因子矩阵之间的映射关系，在误差满足工程要求的条件下，利用F维度低于X的特点(m≤p)，达到缩减计算成本的目的。

1.2FAMO流程

在经典的MO流程方法中，引入因子分析(见图1虚线方框)，在优化数学模型与实验设计之间，替代PSMO的参数筛选过程，形成了FAMO方法流程，具体步骤如下：

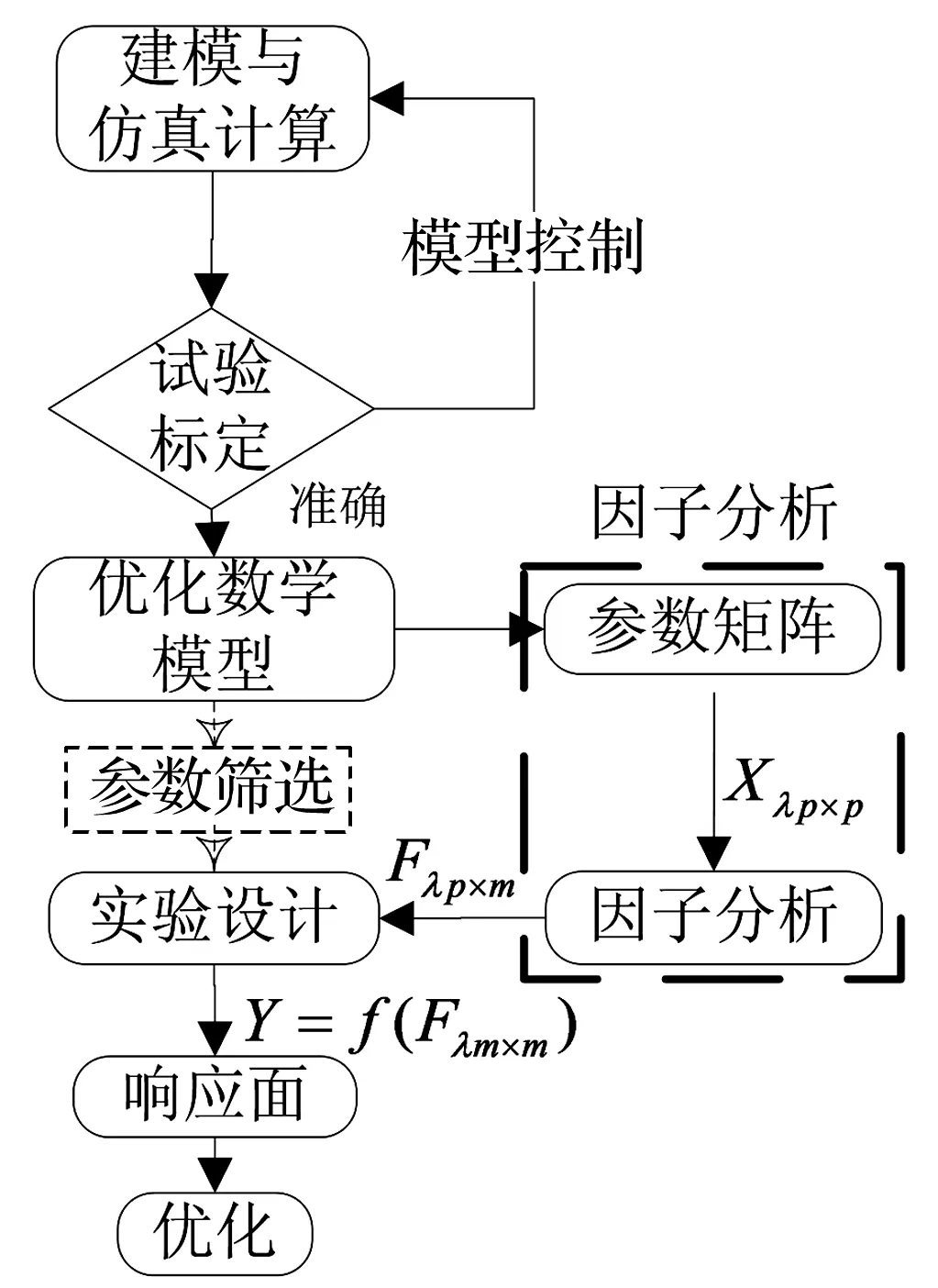
图1　FAMO流程图Fig.1 The flow algorithm of FAMO

1) 建立优化数学模型

在得到准确仿真模型的基础上，确定优化模型的目标函数、约束函数与定义域，一般的优化数学模型形式为：

s.t.g(X)≤0

(3)

2) 建立参数矩阵Xλp×p

利用拉丁超立方(LHS)建立矩阵Xλp×p，其中λ是参数维度p的倍数。由于建立数学模型时，已确定了参数的维度，因此λ决定了优化模型样本空间的大小，在保证足够样本量的前提下，避免过拟合[9-10]，合理对λ取值，从而获得精确、经济的响应面模型。

3) 因子分析

对Xλp×p进行标准化，利用式(1)、(2)得到载荷矩阵A、因子矩阵Fλp×m和得分矩阵Wp×m，建立Xλp×p与Fλp×m的映射关系。

4) 实验设计

由于因子数量为m，利用LHS抽取样本空间为λm的Fλm×m和对应的Xλm×p，通过λm次仿真试验得到目标函数解Yλm。

5) 优化求解

利用Kriging插值建立关于Fλm×m与Yλm的响应面函数(式(4))，最终选择多目标遗传优化(MOGA)算法，对Yλm进行优化求解。

Yλm=f(Fλm×m)=f(Xλm×pWp×m)

(4)

1.3FAMO精度验证

为验证FAMO计算精度，利用优化检验函数Sphere(式(5))、Rastrigrin(式(6))对FAMO与MO的优化精度进行对比，两种检验函数优化解均为0。

(5)

(6)

通过比较FAMO的响应面均方根值(RMSE)与优化解的精度(见表1)，FAMO算法在一定程度上牺牲了精度，但误差满足工程要求，且随参数维度的增加，FAMO所缩减的样本量增加，更节省计算资源。

2爆炸冲击下底部系统响应

为了进行底部系统优化，需要建立爆炸冲击下准确的仿真模型，参考TR-HFM-090[11]试验方法，设置模型的边界条件，对底部系统响应进行仿真研究，并进行相应的验证试验。

2.1底部系统仿真

表1　FAMO与MO方法精度对比

2.2底部系统试验

为了标定仿真模型，参考AEP-55[14]进行底部系统验证试验，场地条件符合GJB349.28-90要求。如图2(b)所示，混合Ⅲ型50分位假人以坐立姿态放置在副驾驶位置，假人的R点与座椅的H点重合，双腿弯曲，小腿平放于驾驶室底板，并采用四点式安全带进行约束，假人需激活其小腿、腰椎与颈椎的传感器。在车辆底部安装CYG401型压力传感器，并使用DH5960数采集仪获取车辆底部爆炸超压。根据底部试验所得到的车辆底部超压(见图2(c))、乘员响应等时间历程曲线，仿真与试验有较高的吻合度。

2.3乘员损伤

车辆防护的目的是保护车内乘员安全，底部系统优化应该以乘员响应(小腿轴向力、颈部力矩、腰椎加速度等)为优化目标。根据仿真与试验结果，乘员响应阶跃现象明显，其中乘员小腿受力峰值为3.90 kN(见图3)，颈部弯矩峰值为21.64 Nm(见图4)，腰椎加速度峰值为33.34 g(见图5)。按AEP-55标准，小腿、颈部响应已接近损伤阈值(小腿受力阈值为5.4 kN，颈部向后弯矩阈值为57 Nm)有必要对底部系统进一步优化，在后续的底部系统优化中将以乘员小腿受力fFt与颈部弯矩fMn为优化目标。

图2　底部系统仿真与试验对比Fig.2 Comparison between numerical analysis and test

图3 小腿轴向力时间历程Fig.3Theaxialforceoftibia图4 颈部力矩时间历程Fig.4Thetorqueofneck图5 腰椎加速度时间历程Fig.5Theaccelerationoflumbar

3底部系统优化

在该底部系统的实际优化设计中(车辆总布置与主断面已确定)，选取其车辆底部结构厚度tb1、tb2、tb3、tb4，座椅支架厚度ts1、ts2、安全带材料弹性模量E，安全带上挂点安装位置h共8个设计参数，对底部系统进行多参数优化。设计参数的初始值及其取值范围如图6、表2所示。

图6　底部系统设计参数Fig.6 The design parameter of vehicle underbody

设计变量初值取值范围①底部板1tb1/mm2015～25②底部板2tb2/mm1612～20③底部板3tb3/mm107～13④底部板4tb4/mm53～7⑤座椅板1ts1/mm21～3⑥座椅板2ts2/mm64～8⑦安全带E/MPa22001900～2500⑧上挂点h/mm0-30～30

根据爆炸冲击作用下底部系统的仿真与试验，乘员的小腿与颈部是最容易受到伤害的部位，以小腿轴向力fFt、颈部弯矩fMn为优化目标；模型中仍然考虑损伤，设腰椎加速度fAs为约束函数；为了避免底部系统质量增加从而影响车辆机动性能，设满载质量fmass为约束函数，在保证响应面精度与避免过拟合的情况下，设λ=5(当λ≥5，响应面精度并没有显著增加)。综上，建立的底部系统设计的优化数学模型：

综上，笔者析得国内正念疗法研究主题相对集中，围绕正念训练、正念、心理健康、正念干预等核心关键词，形成了以躯体疾病、禅修、MBSR、社会生活问题等重点关键词为代表的热点主题，在这些热点主题四周又衔接诸多研究议题。

minY(X)=(fFt,fMn)

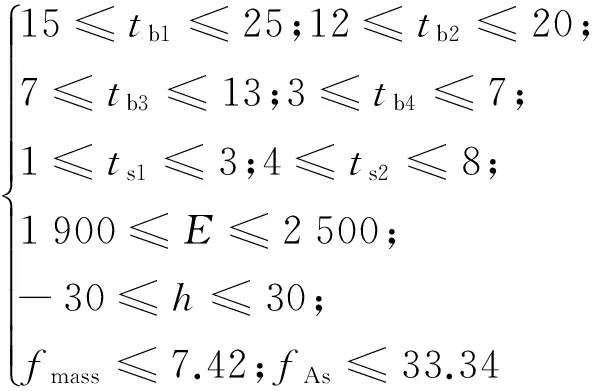
(7)

3.1MO算法

利用MO求解优化数学模型，考虑设计参数间的交互作用，建立参数维度为8，水平数为5，考虑设计参数间交互作用的正交中心复合试验L40(58)，根据所得的样本空间，进行40次爆炸冲击作用下底部系统的仿真计算，并利用Kriging插值建立fFt、fMn的响应面函数，最后使用MOGA进行优化求解。MO的算法流程目前已很成熟，现已集成于各类商业优化软件中，MO能获得准确的优化结果，但所需的样本空间较大,占用计算资源多。

3.2PSMO算法

为了缩减设计参数样空间，是在MO算法流程的基础上利用Plackett-burman采样，建立L12(28)参数筛选试验。结合方差分析(ANOVA)得到出8个参数对2个目标函数的累计贡献率，见图7。

图7　设计参数累计贡献率Fig.7 The contribution rate of design parameters

PSMO在筛去贡献率较低的3个参数E、ts2、h后，针对剩下的5个设计参数，通过样本空间为25的正交中心复合试验L25(55)建立响应面，并最终优化求解。PSMO能有效缩减优化数学模型的样本空间，但Plackett-burman采样以较少的样本空间取舍设计参数，忽略了参数间的交互作用；被筛去的3个参数贡献率占所有参数贡献率的7.97%，筛去参数后将影响优化精度；参数tb4由于累计贡献较大被保留，而tb4是对目标fMn贡献最小的参数，筛选参数的方法将影响优化结果。

3.3FAMO算法

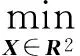
表3　 FAMO的参数矩阵与因子矩阵

3.4优化结果分析

为检验三种算法的优化精度，对仿真结果(经试验标定)与优化数学模型响应面的预测结果进行比较。

MO算法均方根误差最小(见表4)，具有较高的优化精度，PSMO与FAMO为了节省计算资源，缩减了参数的样本空间，在一定程度上牺牲了优化精度。

表4　不同算法的均方根误差对比

1) Pareto解集

对比PSMO与FAMO算法，在参数矩阵的样本空间相同的条件下，FAMO获得了与MO更相似的Pareto解集(见图8)，如采取一定的优化策略(一定权重的优化目标)，利用FAMO将得到与MO更接近的设计方案。

2) 最优解

在底部系统的设计中，如考虑乘员响应函数fFt、fMn同等重要，可在已得到的Pareto解集基础上，利用标准边界交叉法(NBI)[15-16](见式(8))找出其最优解。

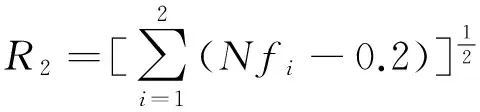
(8)

式中：Nfi为响应函数的标准化结果；fi_max是Pareto解集的最大值；R2为Pareto解集距离原点的欧氏距离，R2最小的解对应最优解，FAMO获得了与MO更接近的最优解(见图9)。

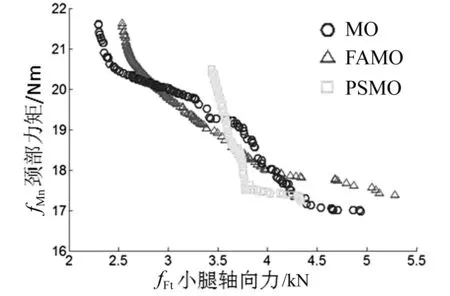
图8　不同算法所得到的Pareto解集Fig.8 The Pareto set from different algorithms

图9　不同算法所得到最优解Fig.9 The ideal solution from different algorithms

3) 最优解的设计方案

由于PSMO筛去了参数E、ts2、h(参数取值等于初始设计)，其最优解对应的设计参数与MO有一定的区别。FAMO通过式(4)计算最优解所对应的设计参数，在底部系统优化中，当乘员响应函数fFt、fMn同等重要时，FAMO获得了与MO更接近的设计方案(见表5)。

表5　不同算法的最优解设计参数对比

4结论

本文针对底部系统的多参数优化问题，在经典的MO流程中，引入多元统计学的因子分析，形成了FAMO方法，通过该算法得到了底部系统的帕累托解集，最终获得了减小乘员损伤的底部系统设计方案，其主要结论如下：

(1) 根据优化检验函数，FAMO算法误差满足工程要求，且随参数维度的增加节省更多的计算资源，适用于底部系统的多参数优化问题；

(2) 在底部系统多参数优化中，使用PSMO能有效缩减样本空间，但其忽略了参数间的交互作用，其筛去的参数、筛选参数的方法都会影响优化结果的精度；

(3) 在底部系统多参数优化中，相对于PSMO，FAMO所得到的Pareto解集、最优解、设计方案与MO更近似，精度更高。

在后续工作中，可使用非线性的降维方法(如最优尺度、拉普拉斯特征映射等)进一步提升底部系统的多参数优化问题的精度。

参 考 文 献

[1] 李红勋, 谭柏春, 贾楠, 等. 美军战术轮式车辆发展策略研究[J]. 军事交通学院学报, 2012, 14(10): 84-87.

LI Hong-xun, TAN Bai-chun, JIA Nan,et al. Research on US military tactic wheeled vehicle strategy[J]. Journal of Military Transportation University, 2012, 14(10): 84-87.

[2] Dharmasena K P, Wadley H N G, Xue Z Y. et al. Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamie loading[J]. International Journal of Impact Engineering, 2008, 35(9): 1063-1074.

[3] 白志海,蒋志刚,严波,等. 金属加筋板局部爆炸冲击荷载研究[J]. 振动与冲击, 2011, 30(12): 93-97.

BAI Zhi-hai, JIANG Zhi-gang, YAN Bo,et al. Localized blast loading of a stiffened metal plate[J]. Journal of Vibration and Shock, 2011, 30(12): 93-97.

[4] Fatt M, Palla L. Analytical modeling of composite sandwich panels under blast loads[J]. Journal of Sandwich Structures and Materials, 2009, 11(4): 357-380.

[5] 李利莎,谢清粮,郑全平, 等. 基于Lagrange, ALE和SPH算法的接触爆炸模拟计算[J].爆破,2011,28(1):18-22.

LI Li-sha, XIE Qing-liang,ZHENG Quan-ping, et al. Numerical simulation of contact explosion based on Lagrange ALE and SPH[J]. Blasting, 2011,28(1):18-22.

[6] Fang H, Rais-Rohani M, Liu Z, et al. A comparative study of metamodeling methods for multiobjective crashworthiness optimization [J].Computers and Structures,2005,83:2121-2136.

[7] Shariyat M, Djamshidi P. Minimizing the engine-induced harshness based on the DOE method and sensitivity analysis of the full vehicle NVH model[J]. International Journal of Automotive Technology, 2009, 10(6): 687-696.

[8] Mechri H E, Capozzoli A, Corrado V. Use of the ANOVA approach for sensitive building energy design[J]. Applied Energy,2010, 87:3073-3083.

[9] Apley D W, Liu J, Chen W.Understanding the effects of model uncertainty in robust design with computer experiments[J]. ASME J Mech Des,2006,128(4):945-958.

[10] Yang R J, Wang N, Tho C H, et al.Metamodeling development for vehicle frontal impact simulation[J]. ASME J Mech Des,2005,127(5):1014-1020.

[11] HFM-090 Task Group 25. TR-HFM-090, Test methodology for protection of vehicle occupants against anti-vehicular landmine effects[S]. RTO/NATO，2007：A1-I18.

[12] MAJ J. NSA/0533-LAND/4569, Protection levels for occupants of logistic and light armored vehicles[S]. 2004：1-B1.

[13] 孙艳馥, 王欣. 爆炸冲击波对人体损伤与防护分析[J]. 火炸药学报, 2008, 31(4): 50-53.

SUN Yan-fu, WANG Xin. Analysis of human body injury due to blast wave and protection method[J]. Chinese Journal of Explosives & Propellants, 2008, 31(4): 50-53.

[14] AEP-55, Volume 2. Procedures for evaluating the protection level of logistic and light armoured vehicles[S]. 2006:1-F6.

[15] Chowdhury R, Rao B N, Meher P A. High dimentional model representation for structural reliability analysis[J].Communication in Numerical Method in Engineering, 2009,25(4):301-337.

[16] Das I, Dennis J E. Normal-boundary intersection: a new method for generating the Pareto surface in nonlinear multicriteria optimization problems[J]. Siam Journal on Optimization，1998, 8(3):631-657.

基金项目：国家自然科学基金项目(51405232)

收稿日期：2015-05-11修改稿收到日期：2015-08-17

通信作者王显会 男，博士，教授，博士生导师,1968年生

中图分类号:TJ81+0.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.014

Multi-parameter optimization of vehicle underbody configuration and occupant restraint system under explosion shock load

WEI Ran, WANG Xian-hui, ZHOU Yun-bo, ZHANG Ming, WANG Liang-mo

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:In order to reduce the vehicle occupant injury under blast wave, a multi-parameter optimization method was proposed for the vehicle hull underbody structure and occupant restraint system. The simulation for the occupant response was based on the arbitrary Lagrange-Eulerian and fluid-solid interaction methods, which was then calibrated by explosion test. An optimization mathematical model for occupant’s leg force and neck bending moment was established, and the thickness, material and locations of vehicle underbody and occupant restraint system were set as design variables. A dimension reduction technique, namely, factor analysis based multi-parameter optimization, was exploited to cut down the sample space of the optimization mathematical model precisely and reasonably. The Pareto set of optimization model was calculated by the proposed methodology, which could get the design scheme of vehicle underbody configuration and occupant restraint system for minimizing occupant injury.

Key words:vehicle underbody configuration; anti-blast performance; multi-parameter optimization; factor analysis; occupant injury

第一作者 魏然 男，博士生，1987年生

E-mail: wxianhui970601@139.com