基于扩展有限元法的连续体结构拓扑优化

印亚荣　伞冰冰

(河海大学 土木与交通学院， 南京　210098)



基于扩展有限元法的连续体结构拓扑优化

印亚荣伞冰冰

(河海大学 土木与交通学院， 南京210098)

摘要：利用扩展有限元法能够在结构内部出现缺陷时无需重新划分网格、简化有限元分析计算的特点，将其与拓扑优化相结合，计算在变密度法的SIMP (Solid isotropic microstructures with penalization)模型下的连续体结构拓扑优化．建立结构在体积约束下的结构拓扑优化模型，将其与结合普通有限元的拓扑优化进行对比分析，对普通结构分析比较结果的一致性表明其对于结构拓扑优化问题的可用性．对有孔洞约束下的平面结构和壳体结构的分析结果表明其对于有缺陷结构拓扑优化问题的网格划分更加简单，最终拓扑图形不会产生由孔洞约束而产生的尖端和应力不均匀现象．

关键词：拓扑优化；扩展有限元；变密度法

结构拓扑优化是结构优化领域研究的热点问题，从研究Michael桁架的离散体结构优化到Bendson和Kikuchi提出连续体拓扑优化的均匀化方法[1]以来，连续体结构拓扑优化的方法不断出现，如渐近结构优化法[2](ESO)、变密度法[3-4]、变厚度法等．Sigmund等对基于变密度法的建模方法进行深入研究，提出了正交各向同性微结构材料惩罚模型法[5](SIMP)，G. L. N. Rozany详细阐述了该模型的主要优势和背景资料．

目前，变密度法成为应用最广泛的拓扑优化方法之一，广泛应用于多种约束和响应的连续体拓扑优化问题．因其理论难度较低，数学模型容易实现、计算效率高，现已被广泛应用．但是Diaz和Sigmund[7]指出，拓扑优化采用有限元方法对设计区域进行离散化时，有时网格的不连续的排列反而使材料具有更好的“虚拟”刚度．这就造成了数值不稳定现象的发生，例如棋盘格式、网格依赖性等问题．

美国西北大学Belytschko教授等人首先提出扩展有限元思想[8]，并将其应用到拓扑优化中[9]，求解结构中有多种材料存在的优化问题．扩展有限元法是以有限元为基本框架，以单位分解为基础，主要针对不连续问题进行研究．其网格划分与结构内部的几何、物理界面无关，克服了在高应力和变形集中区进行高密度网格划分所带来的困难，从而可以克服由于网格问题引起的数值不稳定现象．因此本文利用其扩展有限元法对网格划分的优势，与拓扑优化相结合来解决结构中出现的数值不稳定现象．

由于一般结构的数值不稳定现象发生的不确定性，对于内部有固定孔洞的结构，内部的形式是由孔洞决定的，利用有限元法时肯定会出现局部网格划分不均匀，造成计算量的增大和优化后应力集中的情况．因此本文分析内部具有孔洞的结构，利用ABAQUS软件进行分析优化，对平面结构不直接在结构开孔洞而是在孔洞外侧建立扩展有限元性质的缺陷继而进行拓扑优化，结果证明可以让结构在不提高计算量和无需二次网格过滤的基础上，得到同样具有孔洞且无应力集中的结构．

1SIMP拓扑优化理论

变密度法是从均匀化方法发展来的，它把拓扑优化问题转化为材料的最优分布问题，其基本思想是人为假定一种实际工程中并不存在的密度可变材料单元，从而材料的物理属性可以以材料单元密度函数的形式表达．以区间[0，1]内的密度值为设计变量，直接定义一个经验公式来表达密度与弹性模量间假定的函数关系．继而引入惩罚因子，对设计变量在(0，1)之间的中间密度值进行惩罚，使中间密度值逐渐向0/1两端聚集．这时除了密度靠近1的单元保留下来，其他单元对结构刚度矩阵影响将变得很小，可以忽略不计．由于变密度法设计变量的数量较少，容易通过编程实现，计算效率也比较高，因此得到了广泛的应用．

固体各向同性材料惩罚模型是一种常用的密度-刚度插值模型，从对中间密度的惩罚效果来看，SIMP插值模型的处理效果比RAMP插值模型略好．SIGMUND等对变密度法材料插值模型进行了深入研究[10]，从理论上研究了各种不同变密度法的材料插值模型，证明了中间密度物理意义的存在．

1.1优化的数学模型

基于变密度理论的拓扑优化是以单元相对密度为设计变量，拓扑优化数学模型为：求x={x1，x2，…，xN}T

(1)

图1　SIMP插值模型

p为惩罚系数，p>1会降低中间密度材料的产生，p越大惩罚效果越强，但p太大会引起结构刚度矩阵的病态，以及迭代过度惩罚得不到合理的结果，这里取p=3．

1.2优化算法

优化模型为带不等式约束的非线性规划问题，特点为设计变量多，每个迭代步都要进行结构分析，求解拓扑优化的主流算法可以分为数学规划法[11]、启发式算法和优化准则法[12]3类．

优化准则法是把最优解需要满足的Kuhn-Tucker条件[13]作为最优结构应满足的准则，通过引入Lagrange函数，引入Lagrange乘子，将有约束的非线性优化问题转化为无约束的优化问题．优化准则法下的变密度法拓扑优化就是通过改变密度使得结构目标函数的改变和约束条件的变化相平衡，逐步迭代使得结构满足Kuhn-Tucker所要求的驻值条件．优化准则法要求重分析的次数一般跟变量的数目没有多大关系，收敛速度快，迭代次数少，最主要是和结构的复杂程度和大小无关，所以对中型和大型结构的优化设计有重要的实际意义．

2扩展有限元法

传统有限元对于位移场的描述是基于单元的，每个单元内部的位移场函数总是通过形函数和单元结点位移来表达的：

(2)

扩展有限元法是单位分解方法[14-15]的特例，利用有限元形函数作为单位分解函数，引入非连续位移模式来描述非连续性位移场．扩展有限元法将模型分为：(Ⅰ)在忽略内边界情况下对区域进行网格剖分；(Ⅱ)在单元形状函数中增加与内边界有关的附加函数，改进有限元逼近空间，既得扩展有限元法下全域的位移逼近函数为：

(3)

式中，Ni、Nj为形状函数矩阵，ψj为改进函数．ui表示常规自由度；Ne表示单元改进结点数；Nn表示不存在不连续界面的单元结点数；aj表示单元改进结点上的附加自由度．

对裂纹问题所涉及的两个改进函数描述如下：广义Heaviside函数H(x)：对于裂纹表面采用Heaviside函数H(x)，在裂纹上方H(x)取1，裂纹下方H(x)取-1；裂尖函数ψa(x)：为了模拟裂纹尖端，改善断裂计算中裂尖场的精度，各种问题下裂尖改进函数不相同．

扩展有限元法在模拟裂纹扩展问题的应用最为成熟，可以通过在含有裂纹的结点处增加额外自由度来反映裂纹的存在．相对有限元方法来说，扩展有限元法显著提高了描述复杂位移场的能力，对于处理灵活的非连续边界问题，避免了网格重新划分的工作．对于拓扑优化方法中，利用扩展有限元法复杂内边界的网格划分问题，其优势是去除了可能发生的拓扑图形凹凸或尖端的问题，省去了后期对不稳定现象的二次优化，较好地提高了拓扑优化的效率．

3算例分析

算例1：如图2所示的0.16m×0.1m×0.006m平面矩形悬臂梁结构，材料弹性模量为10GPa，泊松比为0.3，密度为10t/m3，右边界中点施加一集中荷载F=9kN．采用SIMP方法，以结构的最小化应变能为目标函数，体积比小于40%为约束条件，结合扩展有限元法的拓扑优化分析中．以最大主应力失效准则作为扩展起始的依据，最大主应力为300MPa，扩展演化选取基于能量的、线性软化的、混合模式的指数演化规律，粘性系数为0.001．利用ATOM模块计算在减少的体积下，材料的合理排布可以得到的最优刚度解，即得到最优拓扑结构．本例经过51次迭代结构重分析和优化求解后达到收敛状态，图3为拓扑优化结果的mises应力云图．

图2　拓扑模型　　图3　拓扑结果的Mises应力云图

拓扑优化中应变能的迭代变化曲线和体积比迭代变化曲线如图4和图5所示，该拓扑优化过程是在体积比小于40%的基础上将应变能优化到最小值的过程，结构首先满足约束条件体积比的要求，进而进行应变能最小化的进程．表1列出了两次优化结果的应变能、体积比以及最大mises应力的数值结果．

图4　应变能迭代变化曲线　　图5　体积比迭代变化曲线

参数应变能/J最大mises应力/MPaFEM33.4136344.722XFEM33.4089394.428

由于变密度法计算的体积比是结构中有效单元的体积比，与实际删减单元后的体积比不同，所以与实际拓扑迭代过程体积变化不一致．在ATOM模块中进行拓扑优化的计算，结果显示其最优拓扑形式和运用普通有限元法计算的最优拓扑形式几乎相同，一方面说明了结合扩展有限元法的拓扑优化的计算结果正确可用，另一方面表明其为未来结合扩展有限元的拓扑优化进一步的研究提供了一个分析的基础空间．

算例2：由于在实际工程结构中的拓扑优化有额外的实际要求，比如有某一些构件需预留孔洞以满足特定位置的构造要求，就需要结构拓扑优化后的特定位置留有孔洞，对于普通有限元方法而言，可以在算例1结构开孔洞后再进行拓扑优化．利用扩展有限元法对于处理缺陷情况的优势，在其孔洞两侧建立扩展有限元性质的缺陷，由于所需要的孔洞包含在建立的缺陷内部，因此缺陷经过优化过程中的扩展就可以形成所需要的孔洞，如图6是扩展有限元方法下的结构的网格划分情况和最终拓扑图形．该结构经过33次的迭代过程达到收敛状态，图7显示出了其拓扑优化迭代过程图形．

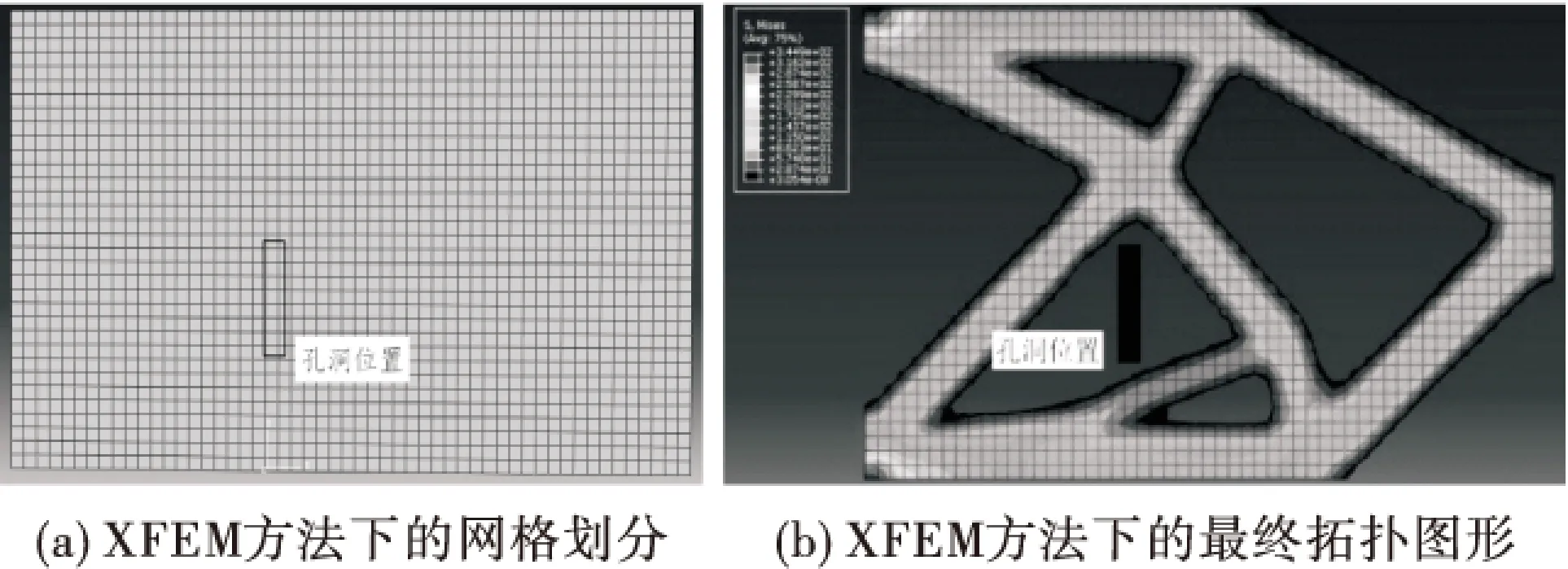
图6　XFEM方法下的起始和最终拓扑图形

图7　XFEM拓扑优化迭代过程

基于普通有限元的拓扑优化经过38次迭代达到收敛，分析结果图形和应变能变化曲线如图8和图9所示．

图8　拓扑优化起始和最终图形

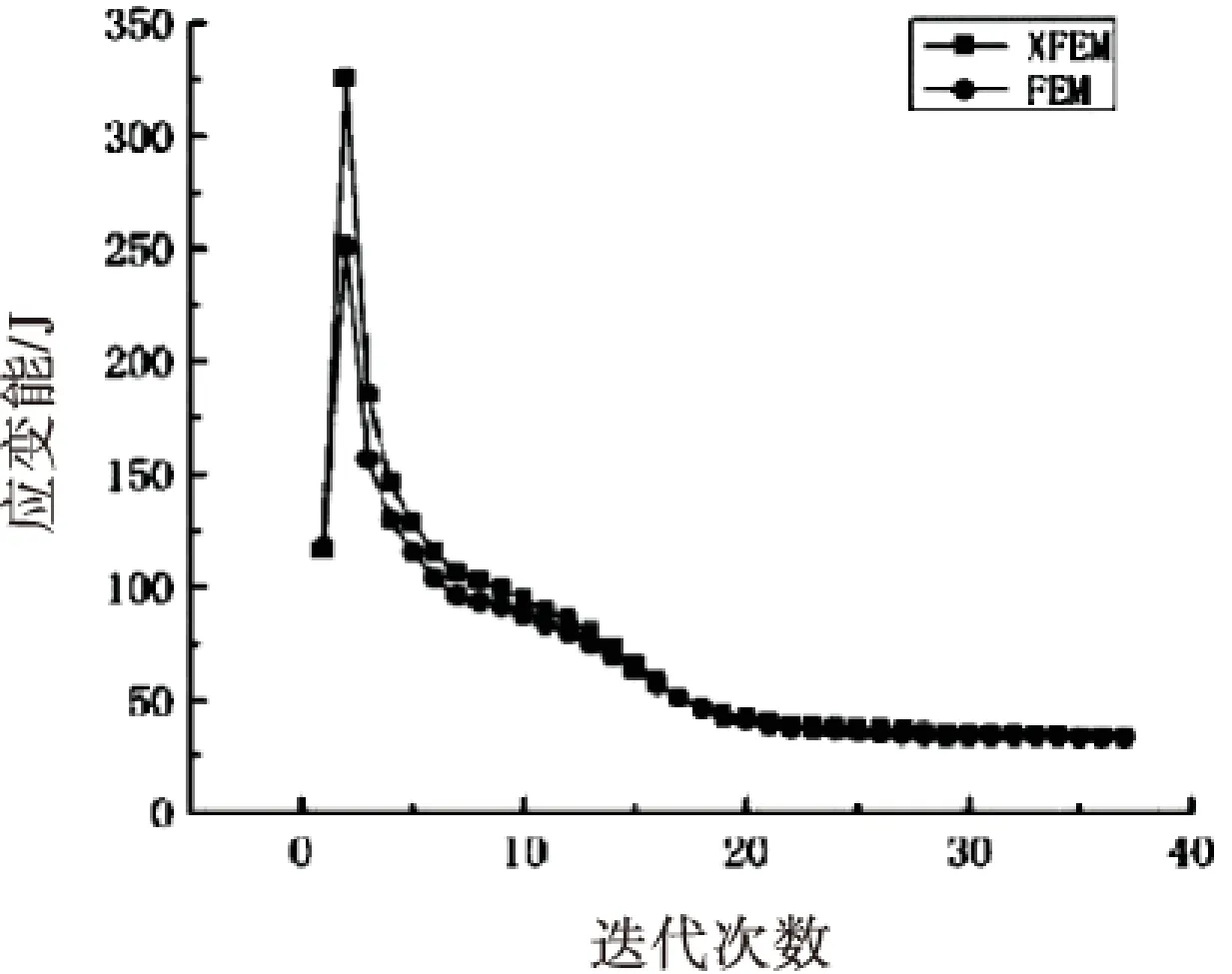
图9　应变能变化曲线

由于孔洞对于结构网格的划分的影响，使得拓扑优化结果的图形在预开洞口的位置会出现尖端，为了使结果更加合理就必须利用网格过滤法对其进行二次优化．基于普通有限元方法的拓扑优化结果显示，在最后变形图中会出现结构的1杆件结构较细、应力值较小的情况，造成了最终拓扑图形不符合所要求的结构形式，不利于在实际工程中的应用．

算例3：如图10所示为双曲扁壳模型，尺寸为1 m×1 m，厚度0.01 m，四角固定，材料的弹性模量为E0=2×1011Pa，泊松比为0.3，集中力F=100 N．结构在中间需开有半径为100 mm的圆形孔洞，网格划分如图11所示．建立SIMP模型，以最小化应变能为目标函数，体积比小于0.4作为约束条件，选取惩罚因子为p=3．

图10　双曲扁曲壳模型　　　　图11　结构网格划分

基于扩展有限元方法下的拓扑优化过程中，经过45次迭代过程达到收敛状态．普通有限元方法下的拓扑优化经过55次迭代达到收敛状态，其拓扑优化结果和应变能的变化曲线如图12和13所示．

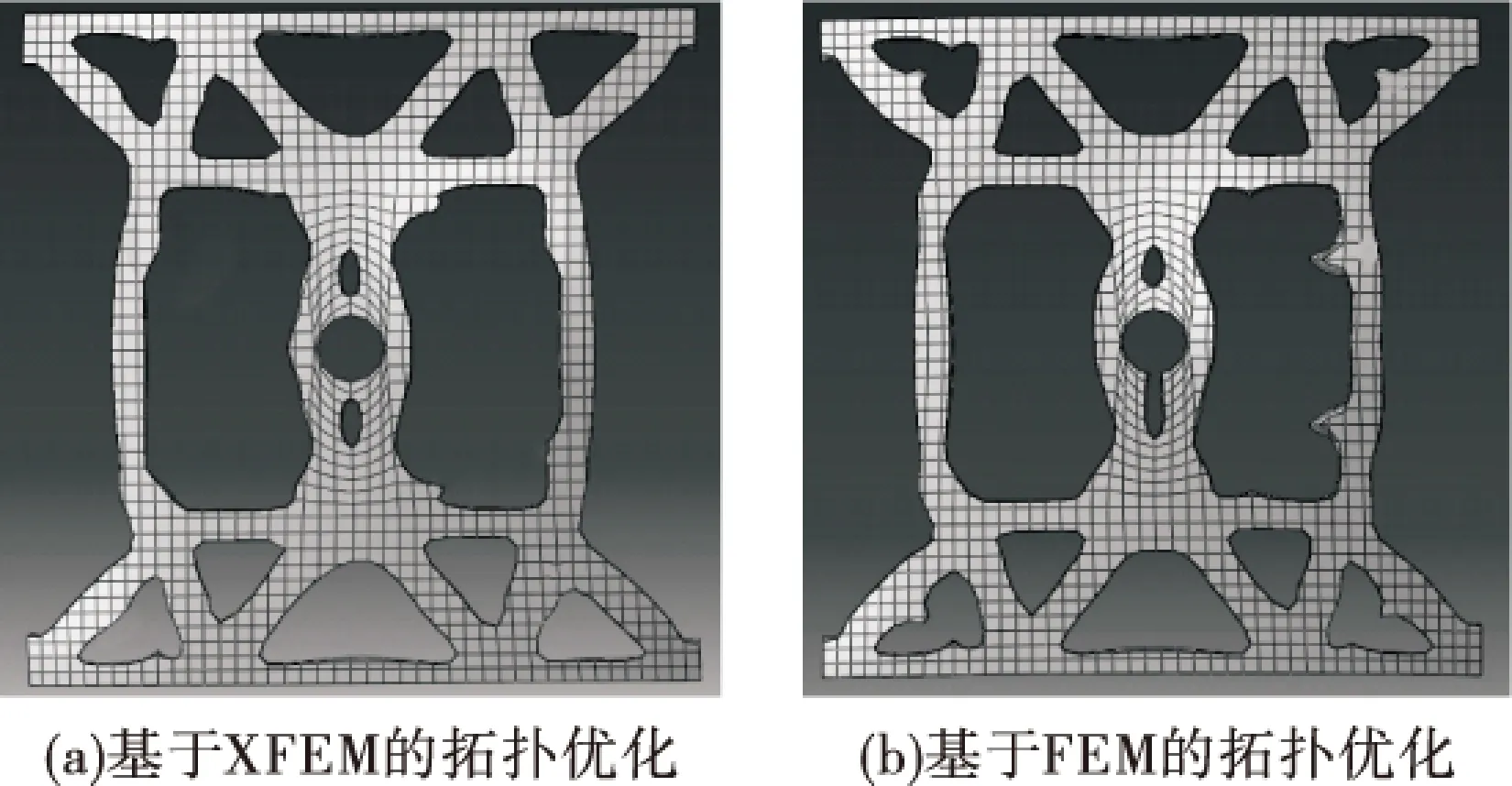
图12　拓扑优化最终图形

图13　应变能变化曲线

两者结果做对比可以看出最终结构在应变能相差不大的情况下，扩展有限元方法收敛速度更快，结果更加简单，其最终结果在满足孔洞要求的同时，其内部边界又更利于操作加工．由于结构受力对称，所以最终优化结构在上下方向处于对称状态，但是普通有限元方法下的结构由于单元网格的划分不能与扩展有限元方法下和缺陷的扩展无关，影响了后期孔洞的形成，在左右方向上并不能和想象的一样处于对称状态．

4结论

1)本文通过将扩展有限元法与拓扑优化方法的结合，利用扩展有限元方法对于网格划分处理的优点，结合SIMP变密度法，对同一模型分别进行普通有限元和扩展有限元方法下的拓扑优化分析，结果表明了基于扩展有限元法的拓扑优化对于结构的优化合理且正确．

2)本文对于需在特定位置留构造孔洞的平面结构和壳体结构分别进行计算比较，结果显示其结果更加合理，在实际中具有较好的实用性．对于平面结构和壳体结构将结构内边界脱离了孔洞的约束，在满足空洞要求的前提下结构的应变能与普通有限元方法下的结果一致，也避免了由于孔洞而可能会出现的结构形式问题和应力问题．

3)本文的计算结果从整体模型来看与前者差距不是很大，但是从应用角度而言其优越性就能体现出来，当计算到体量较大、模型较为复杂的时候，计算效率的优势以及模型局部合理性的优势就会体现出来，更好地为实际工程服务．

参考文献：

[1]Bendsoe M P, Kikuchi N. A Homogenization Method for Shape and Topology Optimization[J]． Computer Methods in Applied Mechanics and Engineering, 1991, 93: 291-381．

[2]Xie Y M, Steven G P. A Simple Evolutionary Procedure for Structural Pptimization[J]． Computers & Structures, 1993, 49(5): 885-896．

[3]Sigmund O. Design of Material Structures Using Topology Optimization: [PhD thesis][M]. Denmark: Department of Solid Mechanics, Technical University of Denmark, 1994．

[4]Sigmund O, Bendsoe M P. Material Interpolations in Topology Optimization[J]． Archive of Applied Mechanics, 1999, 69: 635-654．

[5]Rietz A. Sufficiency of a Finite Exponent in SIMP (Power Law) Methods[J]． Structural and Multidiscipline Optimization, 2001, 21: 159-163．

[6]Stolpe M, Svanberg K. An Alternative Interpolation Scheme for Minimum Compliance Topology Optimization[J]． Structural and Multidiscipline Optimization, 2001, 22: 116-124．

[7]Diaz A R, Sigmund O. Checkerboard Patterns in Layout Optimization[J]． Structural and Multidisciplinary Optimization, 1995, 10: 40-45．

[8]Moes N, Dolbow J, Belytschko T. A Finite Element Method for Crack Growth Without Remeshing[J]． International Journal for Numerical Method in Engineering, 1999, 46: 131-150．

[9]Belytschko T, Xiao S P, Parimi C. Topology Optimization with Implicit Functions and Regularization[J]． International Journal For Numerical Methods In Engineering, 57:1177 - 1196, 2003．

[10] Bendsoe M P, Sigmund O. Material Interpolation Schemes in Topology Optimization[J]． Archive of Applied Mechanics, 1999, 69: 635-654．

[11] Sehmit L A, Mallett R H. Structural Synthesis and Development[J]． Journal of Structural Engineering-American Society of Civil Engineers, 1963, 89(3): 269-299．

[12] Zhou M. An Efficient DCOC Algorithm Based on High-quality Approximation for Problems Including Eigenvalue Constraints[J]． Computer Methods in Applied Mechanics and Engineering, 1995, 128: 3837-394．

[13] Rozvany G I N, Zhou M. The COC Algorithm, part I: Cross-section Optimization Sizing[J]． Computer Methods in Applied Mechanics and Engineering, 1991, 89: 281-308．

[14] Melenk J M, Babuska I. The Partition of Unity Finite Element Method: Basic Theory and Applications [J]． Computer Methods in Applied Mechanics and Engineering, 1996, 139: 289-314．

[15] 李录贤，王铁军. 扩展有限元法(XFEM)及其应用[J]．力学进展， 2005(1)：5-20．

[责任编辑周文凯]

收稿日期：2015-10-20

基金项目：国家自然科学基金资助(项目批准号：51578211)

通信作者：印亚荣(1991-)，男，硕士研究生，研究方向为拓扑优化．E-mail：yinyarong@163.com

DOI：10.13393/j.cnki.issn.1672-948X.2016.01.012

中图分类号：TU311.41

文献标识码：A

文章编号：1672-948X(2016)01-0057-05

Structural Topology Optimization of Continuum Using Extended Finite Element Method

Yin YarongSan Bingbing

(College of Civil & Transportation Engineering, Hohai Univ., Nanjing 210098, China)

AbstractThe extended finite element method can solve the problem when the mesh is splited by crack without remeshing, which can simplify the finite element analysis. We analyze the structural topology optimization of continuum using the Solid isotropic microstructures with penalization, taking full advantage of extended finite element method. The model under the constraint of volume was established using alterable density method for taking the topology optimization with generalized finite element method and that with extended finite element method into comparative analysis. The result supports that the topology optimization using extended finite element method is available and efficient. Then we analyze the original planar and shell structure constraint with a fixed hole, which show topology optimization with extended finite element method can simplify the meshing and eliminate the possibility of producing the tip or inhomogeneous stresses.

Keywordstopology optimization；extended finite element method；alterable density method