气固颗粒系统模拟的研究进展

苏军伟，顾兆林

西安交通大学人居环境与建筑工程学院，陕西 西安 710049

综 述

气固颗粒系统模拟的研究进展

苏军伟，顾兆林

西安交通大学人居环境与建筑工程学院，陕西 西安 710049

综述了气固颗粒系统模拟方法的发展状况。首先，从宏观、中观及直接数值模拟角度对基于欧拉-欧拉架构下的双流体模型、拉格朗日-欧拉架构下的离散气泡模型以及欧拉-拉格朗日架构下的计算流体力学和离散单元法耦合模型（CFD-DEM）及直接数值模拟方法就模型基本原理、计算量、预测精度以及应用前景等方面进行对比和分析。接着，针对工程应用前景较强的双流体模型和CFD-DEM模型进行了详细阐述，着重强调了欧拉架构下的模型植入过程，颗粒相的动力学过程和微观行为描述、两相耦合作用及相间耦合模型描述。基于欧拉-拉格朗日架构下的多相耦合模型的普适性，模型的应用已经从研究尺度的模拟逐渐走向工程尺度的模拟，成为今后研究多相颗粒系统的热点。

颗粒系统 离散单元法 欧拉-拉格朗日方法 群体平衡模型

气固颗粒系统与我们的生活密切相关，广泛存在于自然界和工程领域中，涵盖涵盖对人居环境有重要影响的沙尘暴、气溶胶等自然气固系统和诸如工业流态化反应器、煤粉燃烧器和工业除尘设备等工业设备。在这些系统中，连续相与离散相、离散相与离散相之间存在着非线性、非平均、非稳态、多尺度的复杂相互作用，且这些作用之间存在着复杂的相互耦合。深入研究气固系统的两相及多相动力学行为，对厘清自然气固系统形成及动力学演变过程（比如：沙尘暴的起沙机制，气溶胶的形成机制及尺度演变）等科学问题以及工业设备的性能预测等工程问题具有重要意义。基于作用过程的机理性的模型不受空间维度限制、具有广泛的适应性且可以获取到比实验更为详细的信息。气固颗粒系统的数值模拟在自然现象以及工业设备的研究方面已经得到广泛的应用，相关的数学模型及数值算法也已成为科学界研究的热点问题。

本文在不同架构下对气固颗粒系统模型阐述的基础上，对连续相、离散相及相间作用进行阐述，着重对硬球模型、软球模型、群体平衡模型等多种模型方法的基本思想、发展现状、应用领域以及优缺点进行综述。最后就模拟方法本身、相关模型的耦合进行探讨，给出多相模拟方法的未来发展趋势。

1 概 述

在实际流体的计算中，无论所描述的物质是连续的还是离散的，其描述方法的基础架构无非有两种——欧拉架构和拉格朗日架构。在欧拉架构下，使用雷诺输运定理跟踪物理量在空间域的分布随时间的演变；而在拉格朗日架构下，则通过牛顿第二定律和运动学基本公式来描述流体质点随时间在空在空间分布和实验结果有很大的相似性。

除了双欧拉模型以外，Bokkers等［5］提出的另外一种可以用工程尺度的数值模型——离散气泡模型（discrete bubble model），该模型摒弃了传统的相描述方法而利用拉格朗日方法跟踪连续相气泡，从而可以考虑气泡的碰撞、聚并、破碎、缩小或长大，欧拉描述的并不是实际的颗粒相而是气相和颗粒的混合物。图2给出了Bokkers等对4 m×4 m×4 m的工业尺度流化床的模拟结果。从图中可以看出，通过该方法能够获得气泡的空间分布和尺度分布以及宏观流场。然而，对于气固系统而言，此类方法一般可用于鼓泡床的模拟过程，对于其他流化床的适应性有待验证，方法提出后并未得到长足发展。

1.2 中观模拟方法

中观方法除了关注宏观规律外，还关注系统中颗粒本身的动力学描述以及亚网格内的颗粒相介尺度结构。欧拉-拉格朗日方法是最为典型的中观模拟方法，该方法中用欧拉方法来描述连续相的运动，而用拉格朗日方法来描述系统中颗粒相的运动［6-8］。该方法可以跟踪系统中每个颗粒的运动轨迹，颗粒之间及颗粒与墙之间的作用可以通过离散单元法（DEM）显式地在该模型中体现，计算流体力学和离散单元法耦合模型（CFD-DEM）可以捕捉颗粒相亚格子尺度行为（如：颗粒聚团等各向异性结构）［10］。在该架构下，可以通过大涡模拟的方法考虑连续相的亚格子尺度行为，但相间作用（如：曳力）仍然需要经验公式来封闭。如何准确地将颗粒相及连续相的亚格子尺度行为在相间作用模型中体现，关系着系统的整体行为预测的准确性。跟踪系统中每个颗粒的动力学行为及运动轨迹使得该方法的计算量较大。虽然可以采用颗粒团来代替多个颗粒，但是颗粒团的属性的准确确定及其对系统性能的影响需要进一步研究［24］。该方法的计算量和跟踪的颗粒数目有关，一般适应规模较小，可用于实验室尺度的颗粒系统模拟。

图3 运用CFD-DEM对鼓泡床模拟结果［10］Fig.3 The numerical result of bubbling bed using CFD-DEM method［10］（a） Bokkers’ experimental results［25］； （b） Bokkers’numerical results［25］；（c） Junwei Su‘s 2D numerical results［10］； （d） Junwei Su’s 3D numerical results［10］

图4 运用欧拉-拉格朗日方法对沉浸管流化床模拟结果［10］Fig.4 The numerical results of the immersed tube fluidized bed using Euler-Lagrangian method［10］（a） t=6.10 s； （b） t = 6.20 s； （c） t = 6.30 s； （d） t = 6.40 s； （e） t = 6.50 s； （f） t = 6.60 s； （g） t = 6.70 s； （h） t = 6.80 s； （i） t = 6.90s； （j） t = 7.00 s

图3 给出了运用欧拉-拉格朗日方法对鼓泡床反应器的模拟结果以及和实验的对比。从图中可以看出，数值模拟结果和实验结果有较好的吻合。就气泡大小而言，3D的模拟比2D的模拟更接近实验结果。图4给出了文献［10］运用欧拉-拉格朗日算法对沉浸管流化床数值模拟的结果，显示该方法对气泡行为的预测和实验结果一致，同时可以捕捉到沉浸管附近的颗粒流态分布。

1.3 直接数值模拟方法

直接数值模拟方法（DNS）中，连续相采用欧拉架构描述，离散相采用拉格朗日架构描述。这种方法具有同时捕捉连续相和离散相亚格子尺度行为的特点，相间作用通过颗粒表面流体无滑移条件来完成。该方法虽然计算量过大，很难用于工业规模的计算，但没有引入假设，对探索颗粒流体系统的内在作用机理是必不可少的。尤其是在研究系统下的颗粒表面的质量传递及其反应情况时，这种尺度下的细节信息与当地的流场有密切关系，很难通过实验获得。任意欧拉-拉格朗日（ALE）方法［11］是一种典型的直接数值模拟方法，该方法直接在颗粒表面使用贴体表面网格，且网格点随着颗粒的运动而移动。当模拟一段时间后，网格变形通常很大，需要网格重构，以避免网格过度扭曲。流场信息通常需要在变形前后或者重构前后进行映射，映射过程可能对系统的模拟精度产生影响。避免网格重构及流场映射的方法包含沉浸边界方法［12］和虚拟区域法［13］。这两类方法流体在网格中自由流动，通过颗粒表面的无滑移边界来对流体进行局部约束，但这两种方法计算量较大，只适合小尺度的研究。如果要考虑到颗粒与流体或颗粒之间或颗粒与墙的相互作用而引起的颗粒变形则需要采用流固耦合方法［26］，颗粒与流体的耦合可以采用直接数值模拟方法，只不过需要利用固体力学的数学模型跟踪每个颗粒的变形情况。此类在生物流体力学中运用较广，比如跟踪血液中红细胞的变形情况等，但计算量通常较大，颗粒数目受到严格限制，一般应用于非常小数目的离散相实体的多相流动问题。

图5给出了运用DNS模拟方法和CFD-DEM耦合的方法对2 000个颗粒的颗粒系统进行模拟的结果比较。中间的图为DNS的模拟结果，左边的为DNS计算的局部流场，右边为CFD-DEM计算的结果。从图中可以看出，DNS能够得到更加精细的数值结果。

气固系统的直接数值模拟方法目前主要集中在算法研究，同时该方法计算量较大，很难用于稍大规模的多相颗粒系统。考虑工程应用，本文主要从连续相处理、离散相处理以及相间作用三个方面对宏观模拟方法中的双欧拉模型和中观方法中的欧拉-拉格朗日模型进行详细阐述。

图5 运用DNS方法和CFD-DEM方法对颗粒系统模拟比较［27］Fig.5 Comparisons of numerical predictions between DNS and CFD-DEM［27］

2 连续相处理

两相中连续相描述的差异会引起连续相处理方法的不同。在欧拉架构下，为了得到整个区域的解，通常需要对整个求解区域进行网格划分，将预求解的方程在所划分的网格上进行离散并得到代数方程组，接着选择合适的代数方程求解器对代数方程组进行求解，以得到所划分网格点上求解变量的值。

计算区域网格划分的质量直接关系到方程的求解精度和收敛性。网格分为结构化网格和非结构化网格。结构化网格可以直接通过当前网格的索引找到临近网格的索引而不用事先对网格邻居进行搜索并预先存储，这给方程的离散带来了便利。然而此类网格处理复杂几何的划分时相对比较麻烦，于是就出现了块结构化网格。此类网格在局部域为结构化的，通过几个结构化网格拼接而成，多套网格需要在交界面交换信息，在离散时需要特殊处理。非结构化网格无法直接通过当前网格索引找到邻居网格索引，需要通过网格搜索并预先存储当前网格的周围网格。非结构化网格，具有优良的区域适应性，虽说程序编写上较结构化网格复杂，但具有更好的普适性。因此目前的商业软件（Fluent［28］，CFX［28］，Star CCM+［29］等）大都采用的非结构化网格。另外近几年发展起来的一种多面体网格划分方法，目前商业软件如Star CCM+和Fluent或开源软件OpenFOAM［30］都可以对此类网格下的流场计算进行处理。

对区域进行离散之后，需要通过数值离散方法将求解流体的偏微分方程转化为代数方程。目前，在流体计算中主要采用方法有：有限差分方法、有限容积方法和有限元方法。所谓有限差分就是把连续求解区域上求解变量的函数用定义在离散网格上变量的函数来代替，把原方程中的微分用差分来代替，用连续求和代替方程中的积分，这样原求解的微分方程就转换成代数方程组，求解此方程组即可得到在离散点上的数值解，最后利用插值求解整个求解区域上的数值解。该算法可以得到求解区域的高精度解，但是只适用于结构化网格，处理复杂几何时适应性较差。在有限容积方法中，计算区域被划分为一系列连续但不重合的控制单元，将待解的微分方程对每一个控制单元进行积分，最后得到离散方程组。该方法可以针对任意非结构化的网格，且离散后的方程可以保证守恒性，在流体计算领域应用最广，也是求解欧拉架构下气固系统方程的主流方法。所谓有限元方法，将连续的求解区域离散为一组连续且不重合的单元组合体，用在每个单元内假设的近似函数来分片的表示求解域上待求的未知场函数，近似函数用未知场函数及导数在网格单元各节点的插值函数来完成，将问题从连续的无限自由度转换成离散的有限自由度。该方法最早运用在结构力学问题的求解上，现在已向许多领域进行扩充，不过该方法计算量较大。

通过传统的离散方法将偏微分方程转化为代数方程，需要通过代数方程求解器进行求解。目前常见的代数方程求解器主要有高斯赛德尔方法、共轭梯度法和代数多重网格方法［31］。就计算效率而言，代数多重网格求解方法计算速度较快。代数方程求解后，就可以得到离散单元中心的值，然后通过插值得到计算区域其他点的值。应当指出，由于离散具有局部性，因此得到的代数方程的系数矩阵通常是稀疏矩阵，为了节省存储空间一般采用特殊的存储方式进行存储。

描述连续相流体运动的Navier-Stokes方程压力和速度是耦合的，直接求解耦合方程需要计算量较大，通常采用分离式算法。对于不可压缩流压力速度解耦通常采用Simple系列算法［32，33］。

当连续相用拉格朗日架构下描述时，方程不再通过网格进行离散，而是通过建立当前质点和周围质点的关系来完成的，这是粒子方法与传统网格方法的根本区别。同其他方法一样，该方法一个重要的问题就是计算量过大。邻居粒子的搜索是关系整个过程计算量的一个重要环节。

3 离散相处理

3.1 颗粒间的作用

当局部区域内有颗粒堆积时，颗粒就会发生接触而产生作用力。由于颗粒之间或颗粒与墙壁之间的碰撞为非完全弹性碰撞且存在摩擦，使得系统中的能量在碰撞过程中不断耗散。在特定情况下，如带电颗粒或者湿粘颗粒，颗粒之间还存在非接触力。目前应用于气固系统的接触应力的计算方法主要包括：经验公式、动力学理论方法、硬球模型、软球模型。这些方法的一般比较如表2所示。

对多相颗粒系统而言，当颗粒相在欧拉架构下跟踪时（比如：双流体模型），颗粒碰撞应力一般需要模化，目前主要有两种方法：一种是使用经验公式；另外一种运用动力学理论公式。这两种模型计算量小，可以用于近似计算。此类模型只能计算颗粒碰撞的总体效果，无法体现碰撞细节；且当颗粒之间存在着其他作用力时，这些经验的或者基于动力学理论的描述的颗粒间的作用关系将不再适应，需要重新构造。多相网格质点法（MP-PIC）中颗粒的作用力就是采用的一种经验关系［34］，这使得该方法计算量较小，在对于作用不是很复杂，且计算精度要求不是很高的情况下，可以采用该方法对系统进行模拟。该方法利用颗粒团来代替颗粒，更适合对多分散系统进行描述。

表2 颗粒碰撞力不同计算方法的比较Table 2 Comparisons of different methods for evaluating particle collision force

3.1.1 硬球模型

当颗粒运动剧烈且颗粒稀疏时，发生碰撞的过程认为是瞬态的，可以不考虑颗粒的变形等细节，仅仅关心碰撞后的速度，这种简化处理通常被定义为硬球模型。硬球模型假设每次颗粒的碰撞为二元碰撞，即假设在任意时刻t颗粒i最多和另外一个颗粒j发生碰撞，碰撞点为它们的接触点。稀疏系统的颗粒流动模拟是硬球模型的重要应用之一。图6给出了稀疏颗粒系统内二体碰撞颗粒势能随时间的变化。tcoll为颗粒完成一次碰撞需要的时间，tc为颗粒两次碰撞间的颗粒运动时间。tcoll和tc的比值越小，说明系统的颗粒物越稀疏，硬球模型也就越适合。另外，由于一些材料的微观描述无法获取而造成颗粒之间的作用力无法用颗粒之间的相对位置、相对速度和方向准确地描述时，或者由于材料的非线性或复杂的颗粒形状而造成颗粒之间的作用力很难用连续的力学方法来描述时，也可以利用硬球模型来定量描述颗粒的碰撞行为。

硬球模型是一种事件驱动算法，该类算法的特点是在某一个瞬间整个系统只发生一次碰撞，碰撞后的速度可以通过碰撞前的速度求得。对于硬球和墙的碰撞可以参看文献［35］，也有其他形式的硬球模型［36，37］。颗粒碰撞后，参与碰撞的颗粒的运动速度和角速度将改变。

在给定了恢复系数和摩擦系数之后，硬球模型能够给出碰撞后的颗粒速度和角速度。但是需要通过计算得到下次碰撞的时刻，通常需要从大量颗粒里面找到最先发生碰撞的颗粒对，采用直接搜索需要的时间较长，可以通过直接模拟Monte Carlo（DSMC）方法进行抽样并处理碰撞，具体细节可以参看文献［38］。

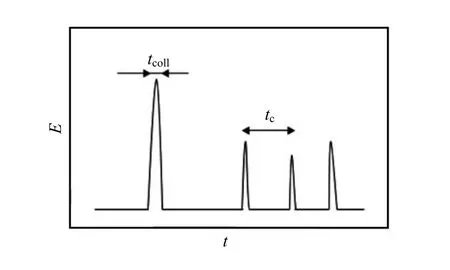
图6 稀疏颗粒系统内二体碰撞颗粒势能随时间变化Fig.6 Evolution of particle potential energy vs time

应当指出硬球模型是事件驱动模型，而欧拉架构下的连续性方程的求解是以时间驱动的。因此，两者耦合较传统的时间驱动的拉格朗日和欧拉耦合更为复杂。在耦合过程中需要考虑下一次碰撞发生的时刻和连续相方程的时间步长的相对大小。其中t时间步长，下一次碰撞发生的时刻tnext，当前发生碰撞的时刻tnow，当：tnext-tnow＞t，则按照t移动颗粒，并记录颗粒这段时间内对流体的反作用冲量，以实现与流体的耦合。将tnow更新，tnow= tnow+t，并重复本步骤，直到：tnext-tnow≤t。

当：tnext-tnow≤t，则按照tnext-tnow移动颗粒，并记录该时间段颗粒对流体的反作用冲量，并累积，以实现与流体的耦合。并将tnow更新，tnow= tnext；重复此步骤，直到：tnext-tnow＞t。

硬球模型的基本思想提出较早，但上世纪80年代后才逐渐被应用到颗粒系统的研究中［39-41］。这些早期的研究仅仅限于简单的物理行为。真正将硬球模型运用于工业系统研究在上世纪90年代中后期。比如，Hoomans等［36，42，43］将硬球模型运用于流化床的模拟，成功预测了气固流化床中气泡的长大、聚并、破碎以及颗粒分离等现象，并讨论了颗粒的物理参数（比如：恢复系数和摩擦系数）对系统的模拟结果的影响，模拟结果经过了实验验证。国内，Ouyang等［37，44］首先将硬球模型运用到了循环流化床系统的模拟，模拟了循环流化床系统稀密共存的非均匀结构及其时空突变行为，讨论了操作条件对非均匀结构形成的影响，成功复现了气泡尾涡和节涌现象。他们的模型复现了垂直传输系统中的塞状流［45］和水平输运系统中的波状流［46］。

采用二元碰撞假设的硬球模型在低速密相颗粒流动中的适用性有待商榷。该模型完全不考虑颗粒受力变形等细节，采用恢复系数和摩擦系数对颗粒碰撞过程予以描述，碰撞后的平移速度和角速度的改变是碰撞过程中力作用的综合结果，且颗粒碰撞过程中不考虑颗粒的变形，因而该方法很难揭示颗粒体系的内在物理机理。该方法更适合快速低浓度的颗粒流动，且很难处理非接触力（比如：液桥力、静电力等），普适性受到了限制。

3.1.2 软球模型

在密相颗粒系统中，某一个颗粒通常同时和多个颗粒发生接触，这时基于二元碰撞假设的硬球模型已不再适应，可以采用软球模型［47］，又称DEM（discrete element method）。该模型最早是用来研究岩石变形的，后来被引入到颗粒散体的研究上。软球模型是一种时间驱动模型，颗粒被视为软性球，通过颗粒的变形、阻尼和滑动来计算每个颗粒的力，并将力对时间的积分来修正每个颗粒的速度。由于在软球模型中需要检测当前颗粒与周围颗粒是否发生碰撞，且计算时间步长比颗粒碰撞的时间间隔要短，因此软球模型的计算量要比硬球模型大的多。因而，计算量问题是软球模型用于工业尺度模拟的一个重要限制因素。由于与连续相流体欧拉方法的求解同属于时间驱动，该算法更容易和CFD耦合进行密相散体模拟计算。模型的相关进展综述可以参看文献［8］。

影响离散单元方法效率的一个重要因素就是颗粒接触的判断，其中最简单的搜索算法是N2搜索算法。此算法实施起来相对比较容易，颗粒的碰撞对象是通过判断该颗粒与其他所有颗粒的相对位置关系后得出的。因此，用此算法确定一个颗粒的碰撞对象需要逐一判断该颗粒与其余N-1个颗粒的位置关系，采用此算法确定整个系统内颗粒的碰撞对象需要搜索过程的数量级为O（N2）。随着颗粒数目的增加，此算法计算量的增加量是显而易见的，因此它不适合用于数量巨大的颗粒系统颗粒碰撞的搜索。另外一种用途较广的算法是邻居搜索算法［48］。此算法将计算区域用颗粒直径分成n个小网格，对每个网格进行编号以确定每个颗粒对应所在的网格。搜索与颗粒i的碰撞列表时，只需要搜索颗粒i所在网格以及它周围8个（三维情况下是26个）相邻网格中的颗粒。辅助网格的大小x：dmax≤x≤2dmax，以保证与当前颗粒碰撞的颗粒只在相邻网格，如图7所示。Munjiza等［49］提出的No-Binary Search算法就是邻居搜索算法。该方法的实施过程：每个颗粒就被分配到一个网格中去，这个网格的编号（I， J）是跟颗粒的坐标（X， Y）关联的，处于（I-1， J），（I-1， J+1），（I， J+1），（I+1， J+1），（I+1， J） ，（I+1， J-1） ，（I，J-1） ，（I-1， J-1）以及（I， J）这些网格中的颗粒就是该颗粒的邻居，颗粒的碰撞对象就在颗粒邻居中寻找，因此这种算法的效率非常高。用该算法判断两个颗粒是否碰撞需要先判断这两个颗粒所处的小网格是否相邻，如果不相邻，肯定不会碰撞；如果相邻，则判断是否碰撞。因此该算法确定整个系统中各个颗粒的碰撞情况需要的搜索过程的数量级仅为N*O（C2）/C，比N2算法速度快。单颗粒网格搜索算法是另外一种高速搜索算法［44］，它用比颗粒直径（非均一直径系统则是最小颗粒直径）还小的网格划分计算区域（即：x＜d）。这样可以保证一个网格中最多会有一个颗粒，搜索碰撞颗粒的范围是颗粒i所在网格周围的n层，n = （ri+ rmax）/x+1，如图8所示在搜索范围之内（中间加黑的方框）判断颗粒之间是否发生碰撞。单颗粒网格法与邻居搜索算法相似，都是采用辅助网格来建立颗粒碰撞列表，区别在于前者颗粒网格中只有一个颗粒，而后者颗粒网格中可以有多个颗粒。对于颗粒尺寸均一或者近似的系统来说，这两种方法的速度相差不大，然而对于颗粒尺寸相差比较大的情况，单颗粒网格搜索算法可以有效地减小搜索范围，但要消耗较大的存储空间。

图7 邻居搜索算法Fig.7 Sketch of the neighbor search method

图8 单颗粒网格搜索算法Fig.8 Sketch of single particle grid search method

除了颗粒间的碰撞检测以外，颗粒与复杂壁面的碰撞检测是离散单元方法工业应用一种重要障碍。为了解决这一问题，苏军伟等［10］发展了颗粒与任意复杂结构的碰撞检测算法——RIGID，为DEM的工程应用奠定了基础。

在离散单元法的应用方面，日本的Tsuji等［50，51］首先将软球模型应用到气固系统的模拟中，得到了与实验一致的最小鼓泡速度、压力波动频率及其不同气速下鼓泡床内颗粒运动信息，并且运用软球模型模拟了水平管道［50］和垂直管道内密相流颗粒的输运过程［52］。随着计算机的发展，软球模型逐渐在颗粒堆积［53-61］、颗粒装卸［62-77］、颗粒混合［78-87］、沉积［88］、颗粒传热［89］和颗粒摩擦起电［90］等颗粒相关的领域得到长足的发展。关于离散单元方法应用可以参看文献［7］。

随着人们研究的深入，离散单元法在非球形颗粒的研究上也得到了一定的发展。目前离散单元法可以针对多边形［91，92］、多面体［93］、二次曲面块体［94，95］进行模拟，但是这些复杂几何体在接触判断及三维扩充时遇到了难题［96］——计算费时。目前比较好的解决方法是用颗粒簇来近似代替实际形状的颗粒［97，98］。

图9 两个球体的碰撞情况Fig.9 Sketch of collision of two sphere particles

离散单元法虽然将颗粒看作软球，但实际上在模拟过程中球体并不发生变形。图9给出了两个球碰撞的情况。实际球体碰撞过程中接触面的形状如虚线所示，而在离散单元法中，并不直接跟踪颗粒的变形，而是通过两球体颗粒的接触面中心重叠量来计算颗粒的受力，因此这是一种近似方法。当颗粒材料（比如：粘弹性材料）属性呈现严重的非线性时，这种近似将不再适应，此时需要采用更加准确的力学模型来计算颗粒的受力。

3.2 多分散特性及其颗粒相微观行为

在气固系统中，颗粒之间除了存在复杂的力学行为外，还存在有聚并、破碎、长大等复杂的颗粒相微观行为。由于颗粒相微观行为的存在，颗粒呈现尺度分布，进而影响颗粒间的力学行为。要考虑颗粒相的微观行为对系统的动力学行为的影响，需引入另外一个有效工具——离散相群体平衡模型［99］。

群体平衡方程通过跟踪离散相颗粒的数值密度的变化来描述实体属性的演变及其引起属性发生演变的原因［100］。在群体平衡模型架构下，对气固系统中实体的坐标变量分为两类：一类是实体“外部”坐标变量，比如时间、空间坐标；另一类是实体“内部”坐标变量，比如实体的大小、温度、成分等这些标识实体本身属性的坐标变量。通过数值密度函数在属性坐标的积分（颗粒分布的矩）来计算系统的平均属性，并将这些平均属性反馈到系统动力学模型中，从而实现微观行为与动力学方程的耦合。两者的耦合一般在一个架构下完成，也就是欧拉架构下群体平衡模型的算法（矩方法［101］或者分组法［102］）和双欧拉模型进行耦合，拉格朗日架构下群体平衡模型的算法和颗粒的拉格朗日跟踪算法进行耦合［103］。为了充分利用欧拉-拉格朗日方法跟踪系统动力学行为的高精度和矩方法跟踪颗粒相微观行为的低计算量，苏军伟将两种算法进行了耦合，并对汽车尾气的扩散过程进行模拟，得到了较好的效果［104］。

20世纪60年代，Hulburt等［105］首先将群体平衡模型引入化工领域。此后由于模型的求解能力问题，群体平衡模型发展缓慢。近年来由于群体平衡模型的数值解法逐步完善，群体平衡模型得到了快速发展［101，102，106-109］。比如，Tan等运用动力学理论提出群体平衡模型中颗粒长大率模型、聚并率模型、破碎率模型、破碎函数模型等，研究流化床的成粒过程以及操作条件的影响，同时运用离散单元法得到的颗粒的细节信息为这些模型提供理论依据［110-112］。同样，Heinrich等［113］依据颗粒筛选、颗粒长大、颗粒聚并、结核等过程模型，运用群体平衡模型模拟流化床的成粒过程，模型的准确性得到了实验证实。Fan等［114］采用特征长度作为内部属性坐标，对流化床系统颗粒的聚并和破碎行为进行模拟，提出了矩直接积分求解法，该方法具有计算量小。

群体平衡模型中微观频度项（聚并率、破碎率等）需要从微观进行封闭，这些项的准确程度关系到多分散系统的整体跟踪精度。对于气固系统而言，相对比较复杂，目前没有一套普适的模型，需要进一步强化在这方面的研究。议。通过EMMS假设的曳力修正基于提升管内颗粒大都以颗粒团的形式存在，这就意味着颗粒通过聚集的形式在管内运动，颗粒的运动是相关的。而基于动力学理论的双流体模型假设颗粒以单个形式存在，颗粒运动类似分子运动完全无序，两者的基本理论相斥［121］，EMMS模型是针对循环流化床提升管的，使用范围广且概念一致的曳力模型需要进一步深入研究。而欧拉-拉格朗日方法并没有双欧拉方法采用的分子运动无序假设，且颗粒碰撞过程中引起的团聚效应可以直接捕捉，将这种有亚格子修正的曳力模型应用到欧拉-拉格朗日架构下似乎更为合理。近些年来也有人将湍流的过滤理论运用到双欧拉里面，得到一些过滤的双欧拉方程和过滤曳力模型，从而得到系统的颗粒分布的异性结构［21］。Sofiane Benyahia运用该曳力模型和EMMS修正的曳力模型对提升管进行的模拟显示，过滤后的曳力模型和EMMS预测的固相分率都较Ergun-Wen & Yu曳力模型计算出来的固相体积分率高，且团聚现象明显［122］。在实际的气固系统中，颗粒分布的异性结构（颗粒聚团）实际上是相间作用和颗粒碰撞能量耗散的双重结果，目前考虑结构的EMMS曳力模型和Filter的曳力模型仅仅是从相间作用着手，而对于颗粒碰撞对颗粒聚团的贡献，则需要进一步深入研究。

目前的曳力模型大都采用是单粒径系统，很少考虑系统的多分散特性对系统曳力计算及其介尺度结构的影响，针对多分散系统内的相间作用需要深入研究。Beetstra等［123］为多分散系统曳力计算提供了一个可行方向。在欧拉-拉格朗日架构下，实际曳力的计算并非是对单个曳力的简单叠加，而是对双欧拉模型中的曳力计算模型进行的修改，使当前网格内的所有颗粒的整体作用效果和双欧拉计算一致，且两相作用满足牛顿第三定律［124］。基于点源的曳力模型要求流体的网格尺度远远大于颗粒的尺度，而颗粒系统的直接数值模拟要求颗粒的尺度远远大于网格的尺度。当网格尺度和颗粒尺度近似时，两种方法都遇到了困难。为了解决这一难题，Su等［125］提出了一种两层网格算法，解除了颗粒尺度和网格尺度的相互依赖，这使得该方法在多分散颗粒系统的应用具有更好的发展空间，然而，其有效性需要进一步验证。

5 总 述

本文对气固颗粒系统的三类模拟算法——宏观模拟方法、中观模拟方法、直接数值模拟方法从方法原理、模拟精细程度以及应用规模进行了比对，并分析回顾了它们在气固体系统应用的优劣性。其中，双欧拉方法日趋成熟，基于其计算量较小的特点，目前该方法仍是工程多相流动的主流方法。欧拉-拉格朗日方法能够得到更为真实的流动结构，计算量较双欧拉方法大，然而随着计算机的发展，该方法势必会从实验室尺度模拟向工程尺度模拟迈进。直接数值模拟方法能够捕捉最为真实的流动细节，目前主要集中在算法研究，该方法计算量最大。

从连续相处理、离散相处理以及相间作用三个方面对宏观模拟方法中的双欧拉模型和中观模拟方法中的欧拉-拉格朗日模型进行了阐述，着重强调了欧拉模型的植入过程，颗粒的动力过程和微观行为、两相耦合模型及耦合过程。CFD-DEM耦合的模型气固系统模拟的最有前途的方法之一。该方法的基本框架已基本成熟，如何从子模型（相间曳力模型、碰撞应力的准确计算等）的完善方面提高该方法对气固系统的预测精度是重点发展方向之一。

［1］ Gidaspow D， Jung J W， Singh R K. Hydrodynamics of fluidization using kinetic theory: an emerging paradigm ［J］. Powder Technol，2004， 148 （2-3）:123-141.

［2］ Enwald H， Peirano E， Almstedt A E. Eulerian two-phase flow theory applied to fluidization ［J］. Int J Multiphase Flow， 1996，22（1345）:21-66.

［3］ Gidaspow D. Multiphase flow and fluidization: Continuum and kinetic theory description ［M］. New York: Academic Press，1994:239-296..

［4］ Gidaspow D， Seo Y C， Ettehadieh B. Hydrodynamics of fluidization-experimental and theoretical bubble sizes in a two-dimensional bed with a jet ［J］. Chem Eng Commun， 1983， 22 （5-6）:253-272.

［5］ Bokkers G A， Laverman J A， Annaland M V， et al. Modelling of large-scale dense gas-solid bubbling fluidised beds using a novel discrete bubble model ［J］. Chem Eng Sci， 2006， 61（17）:5590-5602.

［6］ Deen N G， Annaland M V， Van der Hoef M A， et al. Review of discrete particle modeling of fluidized beds ［J］. Chem Eng Sci， 2007，62（1-2）:28-44.

［7］ Zhu H P， Zhou Z Y， Yang R Y， et al. Discrete particle simulation of particulate systems: A review of major applications and findings ［J］. Chem Eng Sci， 2008， 63（23）:5728-5770.

［8］ Zhu H P， Zhou Z Y， Yang R Y， et al. Discrete particle simulation of particulate systems: Theoretical developments ［J］. Chem Eng Sci，2007， 62（13）:3378-3396.

［9］ Benyahia S， Galvin J E. Estimation of numerical errors related to some basic assumptions in discrete particle methods ［J］. Ind Eng Chem Res， 2010， 49（21）:10588-10605.

［10］ Su J W， Gu Z L， Xu X Y. Discrete element simulation of particle flow in arbitrarilycomplex geometries ［J］. Chem Eng Sci， 2011，66（23）:6069～6088.

［11］ Hirt C W， Amsden A A， Cook J L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds ［J］. J Comput Phys， 1974，14（3）:227-253.

［12］ Uhlmann M. An immersed boundary method with direct forcing for the simulation of particulate flows ［J］. J Comput Phys， 2005，209（2）:448-476.

［13］ Glowinski R， Pan T W， Periaux J. A fictitious domain method for dirichlet problem and applications ［J］. Comput Meth in Appl Mech Eng， 1994， 111（3-4）:283-303.

［14］ Deen N G， Solberg T， Hjertager B H. Large eddy simulation of the gas-liquid flow in a square cross-sectioned bubble column ［J］. Chem Eng Sci， 2001， 56（21-22）:6341-6349.

［15］ Pfleger D， Gomes S， Gilbert N， et al. Hydrodynamic simulations of laboratory scale bubble columns fundamental studies of the Eulerian-Eulerian modelling approach ［J］. Chem Eng Sci， 1999， 54（21）:5091-5099.

［16］ Sokolichin A， Eigenberger G. Applicability of the standard k-epsilon turbulence model to the dynamic simulation of bubble columns: Part I. Detailed numerical simulations ［J］. Chem Eng Sci， 1999， 54（13-14）:2273-2284.

［17］ Andrews A T， Loezos P N， Sundaresan S. Coarse-grid simulation of gas-particle flows in vertical risers ［J］. Ind Eng Chem Res， 2005，44（16）:6022-6037.

［18］ Sundaresan S. Modeling the hydrodynamics of multiphase flow reactors: Current status and challenges ［J］. AIChE J， 2000，46（6）:1102-1105.

［19］ Yang N， Wang W， Ge W， et al. CFD simulation of concurrent-up gas-solid flow in circulating fluidized beds with structure-dependent drag coefficient ［J］. Chem Eng J， 2003， 96（1-3）:71-80.

［20］ Agrawal K， Loezos P N， Syamlal M， et al. The role of meso-scale structures in rapid gas-solid flows ［J］. J Fluid Mech， 2001，445:151-185.

［21］ Igci Y， Andrews A T， Sundaresan S， et al. Filtered two-fluid models for fluidized gas-particle suspensions ［J］. AIChE J， 2008，54（6）:1431-1448.

［22］ Wang J W， Ge W， Li J H. Eulerian simulation of heterogeneous gas-solid flows in CFB risers: EMMS-based sub-grid scale model with a revised cluster description ［J］. Chem Eng Sci， 2008， 63（6）:1553-1571.

［23］ Wang J W， van der Hoef M A， Kuipers J A M. Why the two-fluid model fails to predict the bed expansion characteristics of Geldart A particles in gas-fluidized beds: A tentative answer ［J］. Chem Eng Sci， 2009， 64（3）:622-625.

［24］ Benyahia S， Galvin J E. Estimation of numerical errors related to some basic assumptions in discrete particle methods ［J］. Ind Eng Chem Res， 2010， 49 （21）: 10588-10605.

［25］ Bokkers G A， van Sint Annaland M， Kuipers J A M. Mixing and segregation in a bidisperse gas-solid fluidised bed: a numerical and experimental study ［J］. Powder Technol， 2004， 140（3）:176-186.

［26］ Forster C， Wall W A， Ramm E. Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows ［J］. Comput Meth Appl Mecha Eng， 2007， 196（7）:1278-1293.

［27］ Kriebitzsch S H L， van der Hoef M A， Kuipers J A M. Fully resolved simulation of a gas-fluidized bed: A critical test of DEM models ［J］. Chem Eng Sci， 2013， 91（3）:1-4.

［28］ ANSYS. www.ansys.com. ［EB/OL］. ［2016-02-4］.

［29］ CD-adapco. www.cd-adapco.com. ［EB/OL］. ［2016-02-4］.

［30］ OpenFOAM. www.openfoam.com. ［EB/OL］. ［2016-02-4］.

［31］ Saad Y. Iterative methods for sparse linear systems ［M］. New York: Society for Industrial and Applied Mathematics， 2003:229-247.

［32］ Patankar S. Numerical heat transfer and fluid flow ［M］: Taylor & Francis， 1980:113-135.

［33］ Issa R I. Solution of the implicitly discretised fluid flow equations by operator-splitting ［J］. J Comput Phys， 1986， 62（1）:40-65.

［34］ Andrews M， O'Rourke P. The Multiphase particle-in-cell （MP-PIC） method for dense particulate flows ［J］. Int J Mult Flow， 1996，22（2）:379-402.

［35］ Crowe C， Sommerfeld M， Tsuji Y. multiphase flow with droplets and particles ［M］. New York， 1998:139-149.

［36］ Hoomans B P B， Kuipers J A M， Briels W J， et al. Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidised bed: A hard-sphere approach ［J］. Chem Eng Sci， 1996， 51（1）:99-118.

［37］ Ouyang J， Li J H. Discrete simulations of heterogeneous structure and dynamic behavior in gas-solid fluidization ［J］. Chem Eng Sci，1999， 54（22）:5427-5440.

［38］ 李静海， 欧阳洁， 高士秋， 等. 颗粒流体复杂系统的多尺度模拟 ［M］. 北京: 科学出版社， 2005:200-249.

［39］ Louge M Y， Jenkins J T， Hopkins M A. Computer-simulations of rapid granular shear flows between parallel bumpy boundaries ［J］. Phys Fluids A， 1990， 2（6）:1042-1044.

［40］ Tsuji Y， Morikawa Y， Tanaka T， et al. Numerical-simulation of gas solid 2-phase flow in a two-dimensional horizontal channel ［J］. Int J Mult Flow， 1987， 13（5）:671-684.

［41］ Frank T， Schade K P， Petrak D. Numerical-simulation and experimental investigation of a gas solid 2-phase flow in a horizontal channel［J］. Int J Mult Flow， 1993， 19（1）:187-198.

［42］ Hoomans B P B， Kuipers J A M， van Swaaij W P M. Granular dynamics simulation of segregation phenomena in bubbling gas-fluidised beds ［J］. Powder Technol， 2000， 109（1-3）:41-48.

［43］ Hoomans B P B， Kuipers J A M， Salleh M A M， et al. Experimental validation of granular dynamics simulations of gas-fluidised beds with homogenous in-flow conditions using positron emission particle tracking ［J］. Powder Technol， 2001， 116（2-3）:166-177.

［44］ Ouyang J， Li J H. Particle-motion-resolved discrete model for simulating gas-solid fluidization ［J］. Chem Eng Sci， 1999，54（13-14）:2077-2083.

［45］ 欧阳洁， 孙国刚， Yu Aibing. 垂直管道的塞状流的模拟 ［J］. 过程工程学报， 2003， 3（3）:193-199. Ouyang Jie， Sun Guogang， Yu Aibing. Simulations of plug conveying in a vertical pipe ［J］. The Chinese Journal of Process Engineering，2003， 3（3）:193-199.

［46］ 欧阳洁， 孙国刚， Yu Aibing. 水平气力输送系统中颗粒波状流的模拟［J］. 西北工业大学学报， 2003， 21（6）:671-674. Ouyang Jie， Sun Guogang， Yu Aibing. On simulation wavelike motion of particle conveyed in a horizontal pneumatic pipeline ［J］. Journal of Northwestern Polytechnical University， 2003， 21 （6）: 671-674.

［47］ Cundall P A， Strack O D L. Discrete numerical-model for granular assemblies ［J］. Geotechnique， 1979， 29（1）:47-65.

［48］ Schafer B C， Quigley S F， Chan A H C. Acceleration of the discrete element method （DEM） on a reconfigurable co-processor ［J］. Comput Struct， 2004， 82（20-21）:1707-1718.

［49］ Munjiza A， Andrews K R F. NBS contact detection algorithm for bodies of similar size ［J］. Int J Numer Meth Eng， 1998， 43（1）:131-149.

［50］ Tsuji Y， Tanaka T， Ishida T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe ［J］. Powder Technol， 1992， 71（3）:239-250.

［51］ Tsuji Y， Kawaguchi T， Tanaka T. Discrete particle simulation of two-dimensional fluidized bed ［J］. Powder Technol， 1993， 77（1）:79-87.

［52］ Kawaguchi T， Tanaka T， Tsuji Y. Discrete particle simulation of plug conveying in a vertical pipe ［C］// Proceeding of 6th international conference on bulk materials storage， handing and transporttation， Australia， 1998:321-327.

［53］ Yen K Z Y， Chaki T K. A dynamic simulation of particle rearrangement in powder packings with realistic interactions ［J］. J Appl Phys，1992， 71（7）:3164-3173.

［54］ Zhang Z P， Liu L F， Yuan Y D， et al. A simulation study of the effects of dynamic variables on the packing of spheres ［J］. Powder Technol， 2001， 116（1）:23-32.

［55］ Latham J P， Lu Y， Munjiza A. A random method for simulating loose packs of angular particles using tetrahedral ［J］. Geotechnique， 2001，51（10）:871-879.

［56］ Vollmari K， Oschmann T， Wirtz S， et al. Pressure drop investigations in packings of arbitrary shaped particles ［J］. Powder Technol， 2015，271（2）:109-124.

［57］ Majidi B， Fafard M， Ziegler D， et al. Packing density of irregular shape particles: DEM simulations applied to anode-grade coke aggregates ［J］.Adv Powder Technol， 2015，26（4）:1256-1262.

［58］ Mostofinejad D， Reisi M. A new DEM-based method to predict packing density of coarse aggregates considering their grading and shapes ［J］.Constr Build Mater， 2012， 35:414-420.

［59］ Latham J P， Munjiza A. The modelling of particle systems with real shapes ［J］. Philos Trans R Soc London Ser A， 2004，362（1822）:1953-1972.

［60］ An X Z， Yang R Y， Dong K J， et al. Micromechanical simulation and analysis of one-dimensional vibratory sphere packing ［J］. Phys Rev Lett， 2005， 95（20）:205502.

［61］ Munjiza A， Latham J P. Comparison of experimental and FEM/DEM results for gravitational deposition of identical cubes ［J］. Eng Computations， 2004， 21 （2-4）: 249-264.

［62］ Langston P A， Tuzun U. Continuous potential discrete particle simulations of stress and velocity-fields in hoppers - transition from fluid to granular flow ［J］. Chem Eng Sci， 1994， 49（8）:1259-1275.

［63］ Langston P A， Tuzun U， Heyes D M. Discrete element simulation of granular flow in 2d and 3d hoppers -dependence of discharge rate and wall stress on particle interactions ［J］. Chem Eng Sci， 1995， 50（6）:967-987.

［64］ Langston P A， Tuzun U， Heyes D M. Discrete element simulation of internal-stress and flow-fields in funnel flow hoppers ［J］. Powder Technol， 1995， 85（2）:153-169.

［65］ Langston P A， Nikitidis M S， Tuzun U， et al. Microstructural simulation and imaging of granular flows in two- and three-dimensional hoppers ［J］. Powder Technol， 1997， 94（1）:59-72.

［66］ Langston P A， Al-Awamleh M A， Fraige F Y， et al. Distinct element modelling of non-spherical frictionless particle flow ［J］. Chem Eng Sci， 2004， 59（2）:425-435.

［67］ Ristow G H， Herrmann H J. Forces on the walls and stagnation zones in a hopper filled with granular material ［J］. Physica A， 1995，213（4）:474-481.

［68］ Kohring G A， Melin S， Puhl H， et al. Computer-simulations of critical， nonstationary granular flow-through a hopper ［J］. Comput Methods Appl Mech Eng， 1995， 124（3）:273-281.

［69］ Rong G H， Negi S C， Jofriet J C. Simulation of flow behaviour of bulk solids in bins .1. Model development and validation ［J］. J Agr Eng Res， 1995， 62（4）:247-256.

［70］ Rong G H， Negi S C， Jofriet J C. Simulation of flow behaviour of bulk solids in bins .2. Shear bands， flow corrective inserts and velocity profiles ［J］. J Agr Eng Res， 1995， 62（4）:257-269.

［71］ Fraige F Y， Langston P A. Integration schemes and damping algorithms in distinct element models ［J］. Adv Powder Technol， 2004，15（2）:227-245.

［72］ Kobyłka R， Molenda M. DEM modelling of silo load asymmetry due to eccentric filling and discharge ［J］. Powder Technol， 2013，233（1）:65-71.

［73］ Zhu H P， Yu A B. Micromechanic modeling and analysis of unsteady-state granular flow in a cylindrical hopper ［J］. J Eng Math， 2005，52（1）:307-320.

［74］ Zhu H P， Yu A B. Steady-state granular flow in a 3D cylindrical hopper with flat bottom: macroscopic analysis ［J］. Granul Matter， 2005，7（2-3）:97-107.

［75］ Ketterhagen W R， Curtis J S， Wassgren C R， et al. Granular segregation in discharging cylindrical hoppers: A discrete element and experimental study ［J］. Chem Eng Sci， 2007， 62（22）:6423-6439.

［76］ Ketterhagen W R， Curtis J S， Wassgren C R， et al. Modeling granular segregation in flow from quasi-three-dimensional， wedge-shaped hoppers ［J］. Powder Technol， 2008， 179（3）:126-143.

［77］ Datta A， Mishra B K， Das S P， et al. A DEM analysis of flow characteristics of noncohesive particles in hopper ［J］. Mater Manuf Processes， 2008， 23（2）:196-203.

［78］ Moakher M， Shinbrot T， Muzzio F J. Experimentally validated computations of flow， mixing and segregation of non-cohesive grains in 3D tumbling blenders ［J］. Powder Technol， 2000， 109（1-3）:58-71.

［79］ Kuo H P， Knight P C， Parker D J， et al. The influence of DEM simulation parameters on the particle behaviour in a V-mixer ［J］. Chem Eng Sci， 2002， 57（17）:3621-3638.

［80］ Arratia P E， Duong N H， Muzzio F J， et al. A study of the mixing and segregation mechanisms in the Bohle Tote blender via DEM simulations ［J］. Powder Technol， 2006， 164（1）:50-57.

［81］ Jovanović A， Pezo M， Pezo L， et al. DEM/CFD analysis of granular flow in static mixers ［J］. Powder Technology， 2014，266（11）:240-248.

［82］ Cleary P W. Particulate mixing in a plough share mixer using DEM with realistic shaped particles ［J］. Powder Technol， 2013，248（2）:103-120.

［83］ Alian M， Ein-Mozaffari F， Upreti S R. Analysis of the mixing of solid particles in a plowshare mixer via discrete element method（DEM）［J］. Powder Technol， 2015， 274（5）:77-87.

［84］ Chandratilleke G R， Yu A B， Bridgwater J. A DEM study of the mixing of particles induced by a flat blade ［J］. Chem Eng Sci， 2012，79（37）:54-74.

［85］ Sato Y， Nakamura H， Watano S. Numerical analysis of agitation torque and particle motion in a high shear mixer ［J］. Powder Technol，2008， 186（2）:130-136.

［86］ Chaudhuri B， Muzzio F J， Tomassone M S. Modeling of heat transfer in granular flow in rotating vessels ［J］. Chem Eng Sci， 2006，61（19）:6348-6360.

［87］ Alian M， Ein-Mozaffari F， Upreti S R.， et al. Using discrete element method to analyze the mixing of the solid particles in a slant cone mixer ［J］. Chem Eng Res Des， 2015， 93（1）:318-329.

［88］ Li S Q， Marshall J S. Discrete element simulation of micro-particle deposition on a cylindrical fiber in an array ［J］. J Aerosol Sci， 2007，38（10）:1031-1046.

［89］ Lu L Y， Gu Z L， Lei K B. An inter-particle contact area and time restoration for softening treatment in thermal discrete element modeling［J］. Europhys Lett， 2009， 87:44004.

［90］ Wei W， Gu Z L. Electrification of particulate entrained fluid flows-Mechanisms， applications， and numerical methodology ［J］. Phys Rep，2015， 600:1-53.

［91］ D'Addetta G A， Kun F， Ramm E. On the application of a discrete model to the fracture process of cohesive granular materials ［J］. Granular Matter， 2002， 4 （2）: 77-90.

［92］ Issa J A. Numerical analysis of micromechanical behavior of granular materials ［J］. Eng Computation， 1992， 9（2）:211-223.

［93］ Jerier J F， Imbault D， Donze F V， et al. A geometric algorithm based on tetrahedral meshes to generate a dense polydisperse sphere packing ［J］. Granul Matter， 2009， 11 （1）: 43-52.

［94］ Mustoe G G W. A generalized formulation of the discrete element method ［J］. Eng Computation， 1992， 9（2）:181-190.

［95］ Hogue C. Shape representation and contact detection for discrete element simulations of arbitrary geometries ［J］. Eng Computation，1998， 15（3）:374-390.

［96］ Williams J R， Connor R O. A linear complexity intersection algorithm for discrete element simulation of arbitrary geometries ［J］. Eng Computation， 1995， 12（2）:185-201.

［97］ Cheng Y P， Nakata Y， Bolton M D. Discrete element simulation of crushable soil ［J］. Geotechnique， 2003， 57（7）:633-641.

［98］ Favier J F， Abbaspour-Fard M H， Kremmer M， et al. Shape representation of axisymmetrical， non-spherical particles in discrete element simulation using multi-element model particles ［J］. Eng Computation， 1999， 16（4）:467-480.

［99］ Gerstlauer A， Gahn C， Zhou H. Application of population balances in the chemical industry - current status and future needs ［J］. Chem Eng Sci， 2006， 61（1）:205-217.

［100］ Mahoney D R A. Population balance modeling. Promise for the future ［J］. Chem Eng Sci， 2002， 57（4）:595-606.

［101］ Marchisio D L， Pikturna J T， Fox R O， et al. Quadrature method of moments for population-balance equations ［J］. AIChE J， 2003，49（5）:1266-1276.

［102］ Kumar S， Ramkrishna D. On the solution of population balance equations by discretization-I. A fixed pivot technique ［J］. Chem Eng Sci，1996， 51（8）:1311-1332.

［103］ 赵海波， 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟 ［M］. 北京: 科学出版社， 2008:187-202.

［104］ 苏军伟. 多分散多相系统离散相动力学模型及模拟 ［D］. 西安:西安交通大学， 2011.

［105］ Hulburt H M， Katz S. Some problems in particle technology - a statistical mechanical formulation ［J］. Chem Eng Sci， 1964，19（8）:555-574.

［106］ Su J W， Gu Z L， Li Y， et al. Solution of population balance equation using quadrature method of moments with an adjustable factor ［J］. Chem Eng Sci， 2007， 62（21）:5897-5911.

［107］ Su J W， Gu Z L， Li Y， et al. An adaptive direct quadrature method of moment for population balance equation ［J］. AIChE J， 2008，54（11）:2872-2887.

［108］ Su J W， Gu ZL， Xu XY. Discrete element simulation of particle flow in arbitrarily complex geometries ［J］. Chem Eng Sci， 2011，66（23）:6069-6088.

［109］ Su J W， Gu Z L， Xu X Y. Advances in numerical methods for the solution of population balance equations for disperse phase systems ［J］. Sci China Ser B， 2009， 52（8）:1063-1079.

［110］ Tan H S， Salman A D， Hounslow M J. Kinetics of fluidised bed melt granulation I: The effect of process variables ［J］. Chem Eng Sci，2006， 61（5）:1585-1601.

［111］ Tan H S， Salman A D， Hounslow M J. Kinetics of fluidised bed melt granulation V: Simultaneous modelling of aggregation and breakage ［J］. Chem Eng Sci， 2005， 60（14）:3847-3866.

［112］ Tan H S， Goldschmidt M J V， Boerefijn R， et al. Building population balance model for fluidized bed melt granulation: lessons from kinetic theory of granular flow ［J］. Powder Technol， 2004， 142（2-3）:103-109.

［113］ Heinrich S， Peglow M， Ihlow M， et al. Analysis of the start-up process in continuous fluidized bed spray granulation by population balance modelling ［J］. Chem Eng Sci， 2002， 57（20）:4369-4390.

［114］ Fan R， Marchisio D L， Fox R O. Application of the direct quadrature method of moments to polydisperse gas-solid fluidized beds ［J］. Powder Technol， 2004， 139（1）:7-20.

［115］ 欧阳洁， 李静海. 确定性颗粒轨道模型在流化床模拟中的研究进展 ［J］. 化工学报， 2004， 55（10）:1581-1592. Ouyang Jie， Li Jinghai. Advances of determinate particle-trajectory model in simulation of fluidized beds ［J］. Journa of Chemical Industry and Engineering， 2004， 55（10）:1581-1592.

［116］ Li J， Kuipers J A M. Gas-particle interactions in dense gas-fluidized beds ［J］. Chem Eng Sci， 2003， 58（3-6）:711-718.

［117］ Rong D G， Horio M. Behavior of particles and bubbles around immersed tubes fluidized bed at high temperature and pressure: a DEM simulation ［J］. Int J Multiphase Flow， 2001， 27（1）:89-105.

［118］ Deen N G， Annaland M V， Kuipers J A M. Detailed computational and experimental fluid dynamics of fluidized beds ［J］. Appl Math Model， 2006， 30（11）:1459-1471.

［119］ Wang W， Li T C. Simulation of the clustering phenomenon in a fast fluidized bed: The importance of drag correlation ［J］. Chin J Chem Eng， 2004， 12（3）:335-341.

［120］ Wang J. A review of eulerian simulation of geldart A particles in gas-fluidized beds ［J］. Ind Eng Chem Res， 2009， 48（12）:5567-5577.

［121］ Deen N G， Annaland M V， Kuipers J A M. Detailed computational and experimental fluid dynamics of fluidized beds ［J］. Appl Math Model， 2006， 30（11）:1459-1471.

［122］ Benyahia S. On the effect of subgrid drag closures ［J］. Ind Eng Chem Res， 2010， 49（11）:5122-5131.

［123］ Beetstra R， van der Hoef M A， Kuipers J A M. Numerical study of segregation using a new drag force correlation for polydisperse systems derived from lattice-Boltzmann simulations ［J］. Chem Eng Sci， 2007， 62（1-2）:246-255.

［124］ Xu B H， Yu A B. Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics ［J］. Chem Eng Sci， 1997， 52（16）:2785-2809.

［125］ Su J W， Gu Z L， Chen C G， et al. A two-layer mesh method for discrete element simulation of gas-particle systems with arbitrarily polyhedral mesh ［J］. Int J Numer Meth Eng， 2015， 103（10）:759-780.

Advances in Numerical Simulation of Gas-Solid Particle System

Su Junwei， Gu Zhaolin
School of Human Settlements and Civil Engineering， Xi’an Jiaotong University， Xi’an 710049， China

In this work， the recent development of numerical methods for gas-solid particle system issummarized. Fristly， the two-fluid model under Euler-Eulerian framework， discrete bubble model under lagrange-Eulerian framework， and the computational fluid dynamics and discrete element method coupled model （CFD-DEM） model from macro， meso and DNS（Direct Numerical Simulation） method under Euler-Lagrangian framework are analyzed and compared in terms of principle， computational loads，numerical precision and application prospects. Next， the two-fluid and CFD-DEM models were discussed in details for their promising engineering application prospects with the emphasis on the implant process under Eulerian architecture， the descriptions and models of the particle dynamical process， the micro-behaviors and the inter-phase coupling process. The coupling model of universal multiphase architecture based on Euler-Lagrangian method and its application in simulation has gradually been changing from academic to engineering scale， hence the multi phase particles system is becoming future research hotspot.

particle system； discrete element method； Euler-Lagrangian method； population balance model

O359

A

1001—7631 ( 2016 ) 03—0261—16

2016-02-04；

2016-04-14。

苏军伟（1981—），男，讲师。E-mail:sujunwei@mail.xjtu.edu.cn。

国家自然科学基金（21306145）；国家重大科技专项（2016ZX05011001-002）。