精确延时爆破振动速度峰值预测模型

李顺波， 杨仁树， 杨 军

(1. 中国矿业大学(北京) 力学与建筑工程学院， 北京 100083；2. 北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)



精确延时爆破振动速度峰值预测模型

李顺波1， 杨仁树1， 杨 军2

(1. 中国矿业大学(北京) 力学与建筑工程学院， 北京 100083；2. 北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

摘要：根据几何地震学的基本原理，以单孔爆破振动速度峰值为基础，按照毫秒延时时间间隔建立精确延时逐孔起爆振动峰值预测模型。不仅可以预测爆破振动速度峰值，而且能够直观地展现爆破区域范围内振动峰值的变化情况，并能从保护区域内振动峰值出发，设定合理的毫秒延时间隔时间。根据现场应用数码电子雷管的深孔爆破实验，该方法计算的预测振动峰值与实测振动峰值吻合良好，计算结果可靠性较好，可以在实际工程中推广使用。

关键词：精确延时； 爆破振动； 预测模型； 振动速度峰值

1引言

爆破技术广泛应用于坚硬岩体开挖工程中，其中爆破振动被认为是爆破施工中最严重的危害之一，如因爆破振动过大引起的滑坡、洞室坍塌、建筑物开裂等灾害事故。对爆破振动进行预测是采取有效爆破方案和防护措施的前提，爆破振动强度可以用爆破振动的加速度、速度、位移等来描述，通常以爆破振动峰值振速来描述爆破振动的强度，由于爆破过程及其振动传播过程的复杂性，实际工程中对于爆破振动峰值预测及衰减规律的研究主要以经验公式为主，也有一些理论研究，或者采用数值模拟及其他方法的研究〔1〕。

目前采用经验公式方法( 萨道夫斯基经验公式等) 的振动预测结果并不理想〔2-3〕，新的爆破振动峰值预测方法势在必行〔4〕。人们开始探索基于神经网络、遗传算法、支持向量机等非线性智能工具进行爆破振动预测的新方法〔5-8〕，并取得一定成果。随着数码电子雷管的使用，逐孔起爆成为可能，杨年华等〔9〕给出了一种爆破振动波叠加数值预测方法。本文基于几何地震学理论，给出了一种爆破振动速度峰值预测方法。

2振动速度峰值预测模型

2.1几何地震学理论

当地震波在介质中传播时，在地震波传播范围之内的任意一点，都可以记录波前锋面到这点的时间，可以将波前锋面传播时间记作空间坐标(x,y,z)的函数，即：

t=g(x,y,z)

(1)

由上式就可以确定波前锋面到达任一点的时间，因此可以确定时间的标量场t(x,y,z)，可以将其定义为时间函数。反之，若在给定一定的时间值ti，则可以由时间函数来确定某一个时刻波前面的位置，从而波前锋面方程可以表述为：

g(x,y,z)=ti

(2)

若知道了一系列的时间，就可以确定出各自相应的波前面位置。如果将地震波传播范围简化为一个平面或者一条直线，则其时间场函数将分别变为二元和一元函数，即：

t=g(x,y)

(3)

t=g(x)

(4)

假设在某一时刻t1，地震波波阵面位于S1位置。根据惠更斯原理，S1上各点都可以看作是子波源从t1时刻向外发射的球面子波。经过了时间Δt之后，这些子波的“子波前锋”为半径等于v(x,y,z)Δt的球面，v(x,y,z)为S1上的波速，这些球面的包络面S2即是时间t2的波前锋面，从而可以得知S1和S2之间的法线距离为：

Δn=v(x,y,z)Δt

(5)

时间场波前锋面如图1所示。

图1　时间场波前锋面示意图Fig.1　Schematic diagram of time field wave front

在爆破工程中，高精度数码电子雷管由于延时误差很小，使得其产生的爆破地震波之间的干扰模式可以预测和重复。在单个炮孔起爆的情况下，炸药爆炸产生的冲击波经过衰减成为弹性波向外传播，弹性波传播速度和岩石介质的性质有一定的关系，同时其向外传播的过程可以看作一个球形波前锋面的产生过程。图2给出了单排炮孔。在孔间毫秒延时间隔为1ms时，其从右到左起爆产生的前锋面示意图。

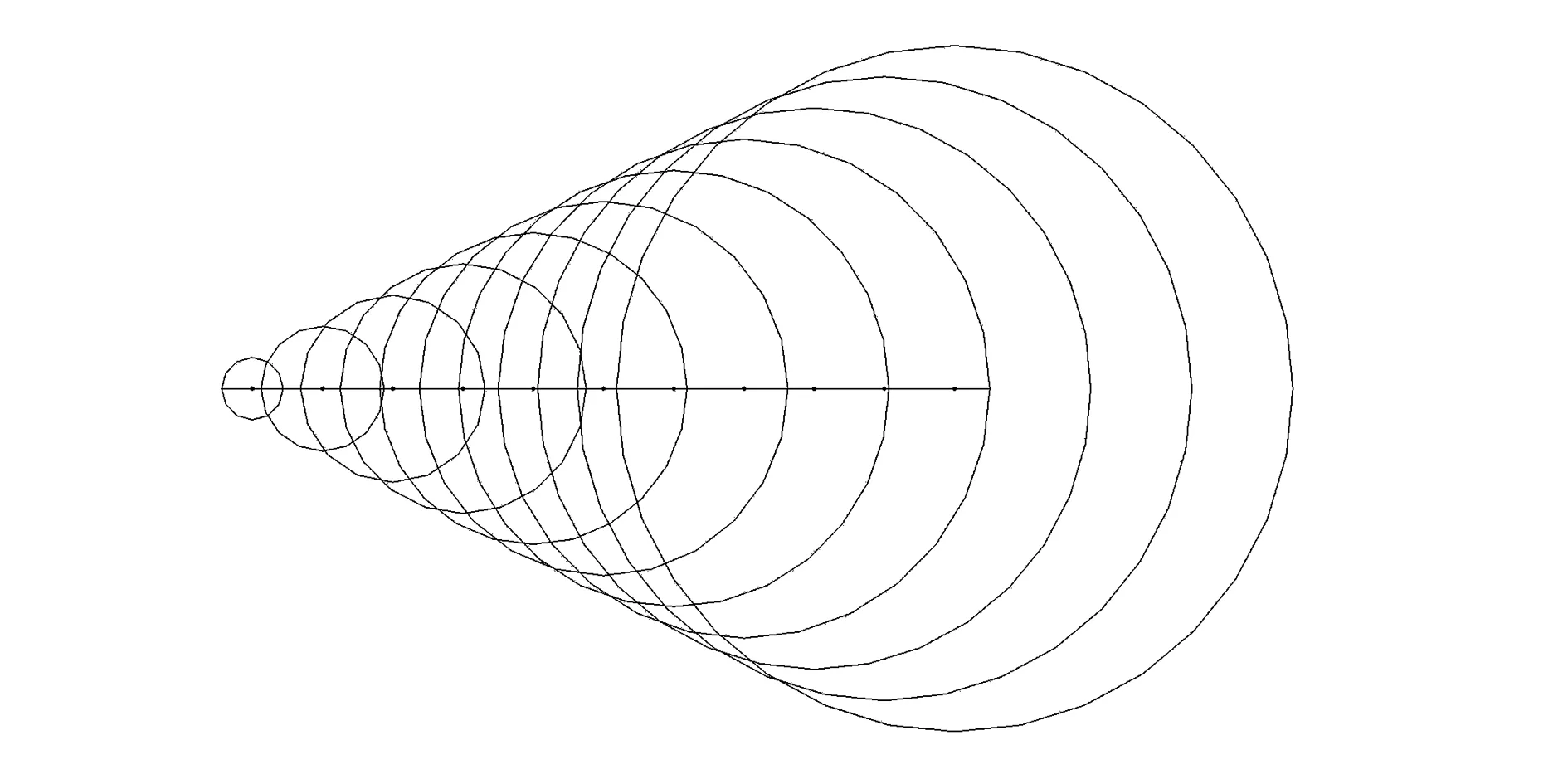
图2　波前锋面产生示意图Fig.2　Schematic diagram of wave front

2.2预测模型的建立和验证

通过前面的分析看出，可以利用岩石介质的纵波波速确定每个炮孔产生的地震波前锋面的位置，若知道单个炮孔装药情况下爆炸产生的地震波速度峰值大小，即可确定波阵面上速度峰值大小。高精度电子雷管的自身误差精度在±1ms，可以实现逐孔起爆，因此最终的波形可以考虑三个炮孔产生的地震波影响。由于纵波波速较快，在第一个炮孔起爆之后，到第三个炮孔起爆这段时间内，地震波传播到较远距离处，后者很难再对前者产生干扰作用。利用图2中的爆破区域，建立精确延时条件下爆破振动速度峰值预测模型。炮孔和测点的相对位置如图3所示，图中爆破区域的炮孔直径为140mm，孔深7 ～9m，单孔药量40 ～90kg，孔间延时18ms。测点M1和M2距爆区142.5m和172.2m。

图3　炮孔和测点位置Fig.3　Position of holes and the measurement points

单孔爆破时两测点波形如图4所示，实测波形如图5所示。从图4和图5中可以读出单个炮孔产生的速度峰值和在两个测点的速度峰值；建立图6的速度峰值预测模型(岩石纵波波速3.6km/s)。从图6中可以看出，在M1和M2点时的波阵面情况，两个测点到其前面的波前锋面法向距离都不相等，在其后的时间内两个测点会受到三个波源的共同影响。因此将在测点之前，由三个波源产生的波前锋面个数定义为其累积效用，由两个测点在单孔波形中的爆破振动速度峰值可以确定其具体强度，从而得到测点在所有炮孔起爆后的爆破振动速度峰值。

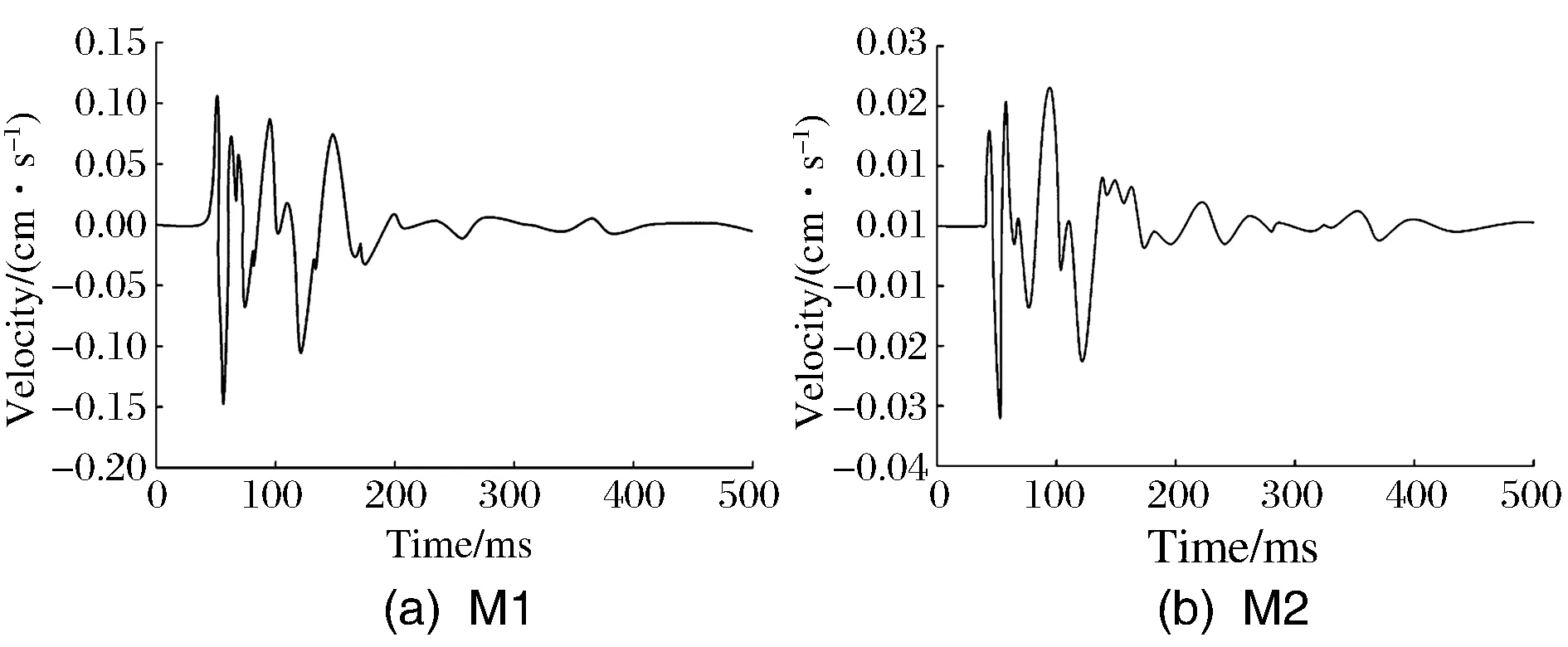
图4　单孔爆破时两测点波形Fig.4　Two measurement points waveform in single hole blasting

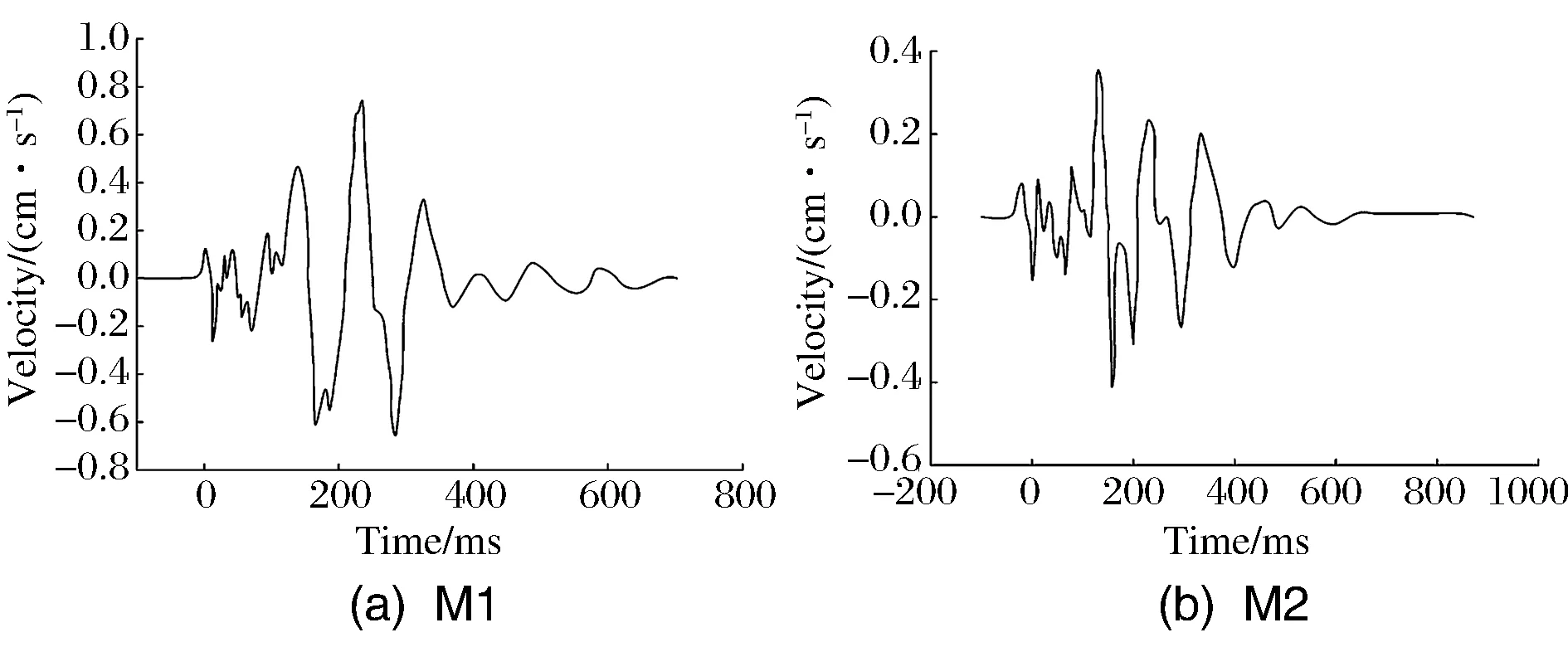
图5　实测波形Fig.5　Measured waveform

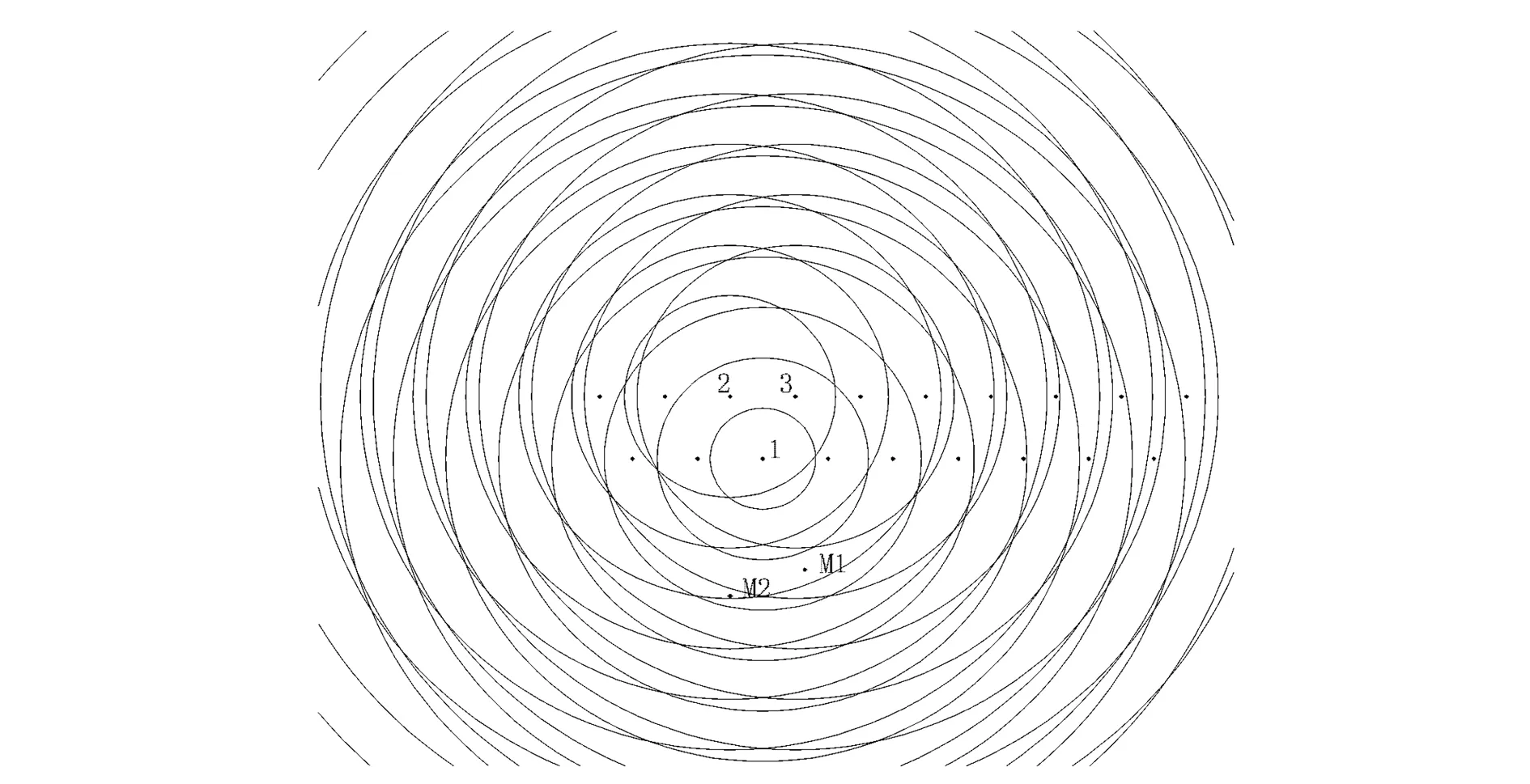
图6　孔间延时间隔18 ms时爆破振动峰值预测结果Fig.6　Blasting peak vibration velocity prediction result at 18 ms hole delay time

模型预测峰值对比见表1。

表1中给出了预测速度峰值和实测速度峰值，可以看出，M1点正向速度预测峰值和实测速度峰值差距较小，M1点负向预测值和M2点预测值与实测值在误差较大，但总体平均误差在20%左右，其预测模型预测值具有一定的可信度。

孔间延时间隔12，9，7，4ms时爆破振动峰值预测结果分别如图7～图10所示。在图7中M1点和M2点到波源1、2、3所形成波阵面法向距离不相等，因此在之后的某一个时刻，受到波源的共同影响；在图8中，中M1点和M2点到波源1、2、3所形成波前锋面法向距离不相等，因此在之后的某一个时刻，受到波源的共同影响；在图9中〔9〕，M1点在波源1波阵面上，因此主要受到波源1的影响，由此可以计算出其位置处的速度峰值大小，同样M2点也在波源1波前锋面上，从而可以计算其振动速度峰值大小；在图10中，M1点到波源1、2、3所形成波前锋面法向距离不相等，因此在之后的某一个时刻，受到波源的共同影响，M2点分别在波源2的波前锋面上，因此主要受到波源的影响，由此可以计算出其速度峰值大小。

表1　模型预测峰值对比

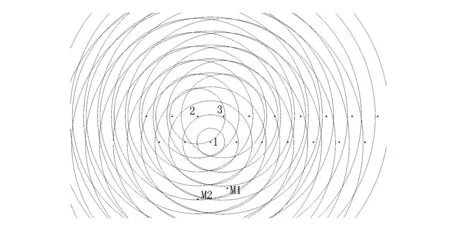
图7　孔间延时间隔12 ms时爆破振动峰值预测结果Fig.7　Blasting peak vibration velocity prediction result at 12 ms hole delay time

图8　孔间延时间隔9 ms时爆破振动峰值预测结果Fig.8　Blasting peak vibration velocity prediction result at 9 ms hole delay time

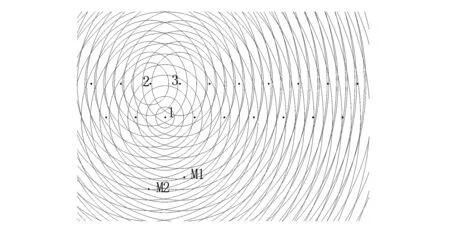
图9　孔间延时间隔7 ms时爆破振动峰值预测结果Fig.9　Blasting peak vibration velocity prediction result at 7 ms hole delay time

不同毫秒延时间隔预测速度峰值见表2。

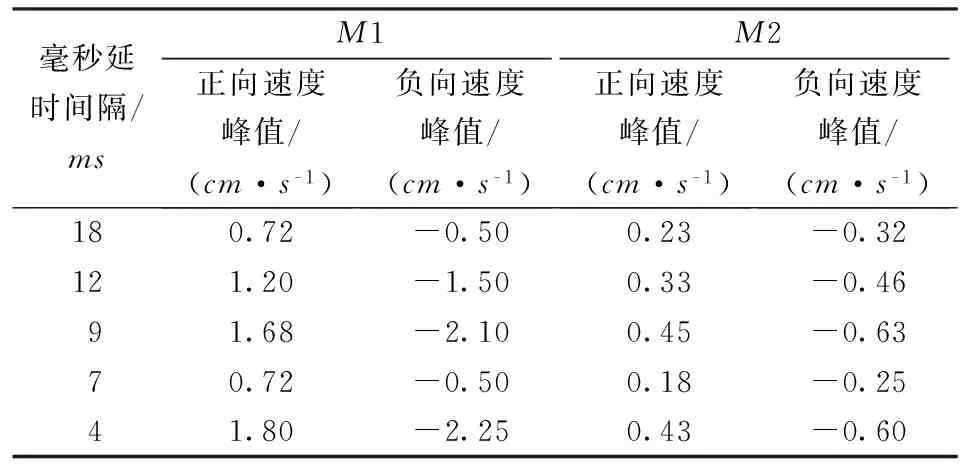
表2　不同毫秒延时间隔预测速度峰值

图10　孔间延时间隔4 ms时爆破振动峰值预测结果Fig.10　Blasting peak vibration velocity prediction result at 4 ms hole delay time

从表2中可以看出，在毫秒延时间隔为12ms时的振动速度峰值要大于毫秒延时间隔18ms时的振动速度峰值；在毫秒延时间隔为9ms情况下，其产生的振动速度峰值要小于毫秒延时间隔为4ms时，但远大于其他三种情况；毫秒延时间隔为4ms时振动速度峰值预测值较大；在毫秒延时间隔为7ms时M1点速度峰值和18ms较为接近，M2点速度峰值较小；从不同毫秒延时间隔的预测模型图中，可以看出不同毫秒延时间隔对波形之间相互干涉作用，可以看出其增强和减弱的所在区域。

3结论

通过和实际工程中爆破振动峰值对比，建立的爆破振动峰值预测模型的误差在20%左右。爆破振动参数的预报分析不仅局限于振动峰值速度，同时给出了一个爆破区域范围内任意一点的爆破振动峰值增强和减弱所在的区域，并能根据需要保护的区域，来选取合理的毫秒延时间隔。精确延时爆破振动峰值预测模型在工程实际应用中不必选用经验系数，避免了人为因素影响，工程可行性更强，便于在实际工程中推广。

参考文献(References)：

〔1〕 易长平，冯林，王刚，等. 爆破振动预测研究综述[J]. 现代矿业,2011,27(5):1-5.

YIChang-ping，FENGLin，WANGGang，etal.Summaryofblastingvibrationprediction[J].ModernMining,2011，27(5):1-5.

〔2〕SINGBTN.Artificialneuralnetworkapproachforpredictionandcontrolofgroundvibrationinmines[J].MiningTechnology,2004,14(4):251-256.

〔3〕 徐全军,刘强,聂渝军,等. 爆破地震峰值预报神经网络研究[J]. 爆炸与冲击，1999,19(2)：38-43.

XUQuan-jun,LIUQiang,NIEYu-jun,etal.Studyofneuralnetworkpredictiononpeakparticleamplitudeofblastinggroundvibration[J].ExplosionandShockWaves, 1999,19(2):38-43.

〔4〕 言志信，言涅，江平，等.爆破振动峰值速度预报方法探讨[J].振动与冲击.2010，29(5):179-182.

YANZhi-xin,YANNie,JIANGPing，etal.Predictionmethodsforblasting-inducedgroundvibrationvelocity[J].JournalofVibrationandShock, 2010，29(5):179-182.

〔5〕 赵华兵，龙源，刘好全，等. 城市隧道爆破振动速度峰值预测神经网络法应用[J]. 工程爆破，2014,20(5)：23-27.

ZHAOHua-bing,LONGYuan,LIUHao-quan,etal.Applicationofneuralnetworktopredictionofpeakamplitudeofblastingvibrationvelocityofurbantunnel[J].EngineeringBlasting,2014,20(5):23-27.

〔6〕 张艺峰，姚道平，谢志招. 基于BP神经网络的爆破振动峰值及主频预测[J]. 工程地球物理学报，2008，5(2):222-226.

ZHANGYi-feng,YAODao-ping,XIEZhi-zhao.Thepredictionofblastingvibrationpeakvalue&mainfrequencybyBPneuralnetwork[J].ChineseJournalofEngineeringGeophysics,2008，5(2):222-226.

〔7〕 文建华，李新平，张文成，等. 复合遗传算法在爆破震动测试参数确定中的研究[J]. 岩土力学，2005,26(1):160-162.

WENJian-hua,LIXin-ping,ZHANGWen-cheng,etal.Astudyofparameterinversionofblastingvibrationbasedoncompositelygeneticalgorithm[J].RockandSoilMechanic, 2005，26(1):160-162.

〔8〕 史秀志，董凯程，邱贤阳，等. 基于支持向量机回归爆破振动速度预测分析[J]. 工程爆破，2009,28(7):28-30.

SHIXiu-zhi,DONGKai-cheng,QIUXian-yang，etal.Analysisoftheppvpredictionofblastingvibrationbasedonsupportvectormachineregression[J].EngineeringBlasting, 2009,28(7):28-30.

〔9〕 杨年华,张乐. 爆破振动波叠加数值预测方法[J]. 爆炸与冲击,2012,32(1):84-91.

YANGNian-hua,ZHANGLe.Blastingvibrationwaveformpredictionmethodbasedonsuperpositionprinciple[J].ExplosionandShockWaves,2012,32(1):84-91.

文章编号：1006-7051(2016)03-0079-04

收稿日期：2015-11-20

作者简介：李顺波(1985-)，男，博士，从事岩石爆破理论方面的工作。 E-mail： lshunbo@126.com

中图分类号：TD235.4+7

文献标识码：A

doi：10.3969/j.issn.1006-7051.2016.03.017

Peakvibrationvelocitypredictionmodelofprecisiondelayblasting

LIShun-bo1,YANGRen-shu1,YANGJun2

(1.SchoolofMechanic&CivilEngineering，ChinaUniversityofMining&Technology(Beijing)，Beijing100083，China；2.StateKeyLaboratoryofExplosionScienceandTechnology，BeijingInstituteofTechnology，Beijing100081，China)

ABSTRACT：According to the basic principle of geometric seismology, with single hole blasting peak vibration velocity as basis and in accordance with the millisecond delay interval,the peak vibration velocity model of precision delay blasing with hole by hole was established.The results showed that the developed method could be used to predict the blasting vibration velocity peaks, it also could intuitively show the variation of blasting peak vibration velocity in the region and reasonable millisecond delay interval was set from the peak in protection region. The calculated velocity was coincident with the recorded ones in the deep hole blasting tests using electronic detonators. It indicated that the developed predication method was reliable for engineering applications.

KEY WORDS:Precision delay； Blasting vibration； Prediction model; Peak vibration velocity