基于SPH方法的爆炸压实孔隙塌缩模拟
李晓杰, 陈 翔, 闫鸿浩, 王小红, 王宇新
(大连理工大学 a. 工程力学系, b. 工业装备结构分析国家重点实验室, 辽宁大连 116024)
基于SPH方法的爆炸压实孔隙塌缩模拟
李晓杰a,b, 陈 翔a, 闫鸿浩a, 王小红a, 王宇新a
(大连理工大学 a. 工程力学系, b. 工业装备结构分析国家重点实验室, 辽宁大连 116024)
摘要:SPH无网格方法适用于大变形问题的数值模拟,近年来一直是研究的热点。爆炸压实过程中孔隙的闭合程度对压实效果起着至关重要的作用。运用AUTODYN软件中的SPH方法对爆炸压实中颗粒间的孔隙闭合过程进行模拟,将模型简化为密排球堆模型中的正三角孔隙闭合模型与倒三角孔隙闭合模型。模拟铜颗粒的孔隙闭合,选用Johnson-Cook本构模型和Hugoniot冲击关系,加载条件为速度加载。根据数值模拟得到的应力分布图、速度分布图、大塑性变形及碰撞点切线的速度分布曲线,可以得出爆炸压实过程中存在着微爆炸焊接、微摩擦焊接、射流侵彻、大塑性变性等过程。不同的孔隙闭合方式下所产生的沉能机制与理论分析得出的相符合。
关键词:爆炸压实; SPH; 孔隙塌缩; 沉能机制; 数值模拟
1引言
爆炸压实是利用炸药爆轰或高压射弹产生激波作用于金属或非金属粉末,在极短的时间内发生高温、高压烧结的一种材料加工的新技术〔1〕。爆炸压实前需要先将粉末预压实到一定的密度,然后烧结成多孔体,爆炸压实过程实际是多孔体在冲击载荷下发生孔隙塌缩、闭合,最终形成致密块体的过程。孔隙的闭合程度及闭合数量直接影响着最终压实体的致密度,因此对爆炸压实过程中的孔隙塌缩问题进行研究有着十分重要的意义。爆炸压实孔隙塌缩过程是一种强瞬时性、强非线性和强耦合的复杂系统〔2〕。目前只有在各种简化模型下才可以得出解析解,因此数值模拟方法成为研究爆炸压实孔隙塌缩过程及机理的一种重要手段。NEMAT N S等〔3〕运用有限元程序对爆炸载荷下铜中单个圆形孔隙的塌缩过程进行模拟,载荷爆压为4 GPa,圆孔直径为10 mm,得到的数值模拟结果与实验结果相符合。COOPER S R等〔4〕利用二维欧拉流体动力学程序对无氧铜中的单个圆孔在冲击波载荷下的塌缩过程进行了数值模拟,并对孔隙塌缩过程中的温度分布进行了分析。TRAN L等〔5〕则利用二维欧拉流体动力学程序对不同冲击速度下无氧铜中的单个圆孔塌缩过程进行了数值模拟,得出不同冲击速度下圆孔塌缩的形状变化。赵峥等〔6〕运用SPH方法对爆炸压实过程中颗粒碰撞问题进行模拟,模拟出了微射流的产生及孔隙塌缩闭合过程,并运用LS-DYNA有限元程序对无氧铜中的圆形孔隙坍缩过程进行了数值模拟,得出在6 GPa的冲击压力下,孔隙闭合时不同边界区域会发生爆炸焊接和射流侵彻。然而目前并没有将模拟与粉末压实沉能机制很好的结合在一起进行分析。因此本文运用AUTODYN软件中的SPH方法对铜粉压实过程中孔隙闭合方式进行模拟,并结合爆炸压实沉能机制对爆炸压实孔隙闭合过程进行理论分析。
2爆炸压实沉能机制
由于粉末材料的颗粒排列通常是无规则的,难以分析。为了将粉末的微观冲击运动机制限制在二维平面内以便分析各种沉能机制,一般采用密排球堆积模型,如图1所示。
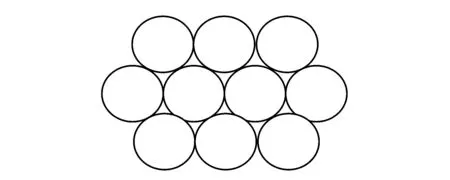
图1 密排球堆积模型Fig.1 Dense accumulation model of the ball
二维密排球堆积模型中的孔隙近似为三角形,存在两种形式:一种是上面两个颗粒、下面一个颗粒的正三角形孔隙,如图2(a)所示;一种是上面一个颗粒、下面两个颗粒的倒三角形孔隙,如图2(b)所示。两者的构成方式不同,闭合过程也不同。
关于爆炸粉末压实过程中颗粒间的沉能机制,国内外学者进行了大量研究〔8-13〕,其中主要包括微爆炸焊接、微摩擦焊接和微孔隙塌缩等沉能机制。正三角孔隙闭合时,A处发生颗粒间的斜碰撞,当碰撞速度小于爆炸焊接下限时,在碰撞点切线方向存在vτ,所以该处的主要结合方式是微摩擦焊接,当vτ=0时,则发生的是正碰撞;当碰撞的速度足够大时,该处的主要结合方式是微爆炸焊接。B处的沉能机制主要是上排颗粒间相互挤压产生的射流侵彻进入下排颗粒的顶部,在这个过程中同排颗粒间产生微爆炸焊接。倒三角孔隙闭合时,上下排颗粒界面处与正三角孔隙闭合时A处的沉能机制相同。C处的沉能机制主要是上排颗粒的大塑性变形。D处的沉能机制是同排颗粒间的相互挤压产生的大塑性变形。
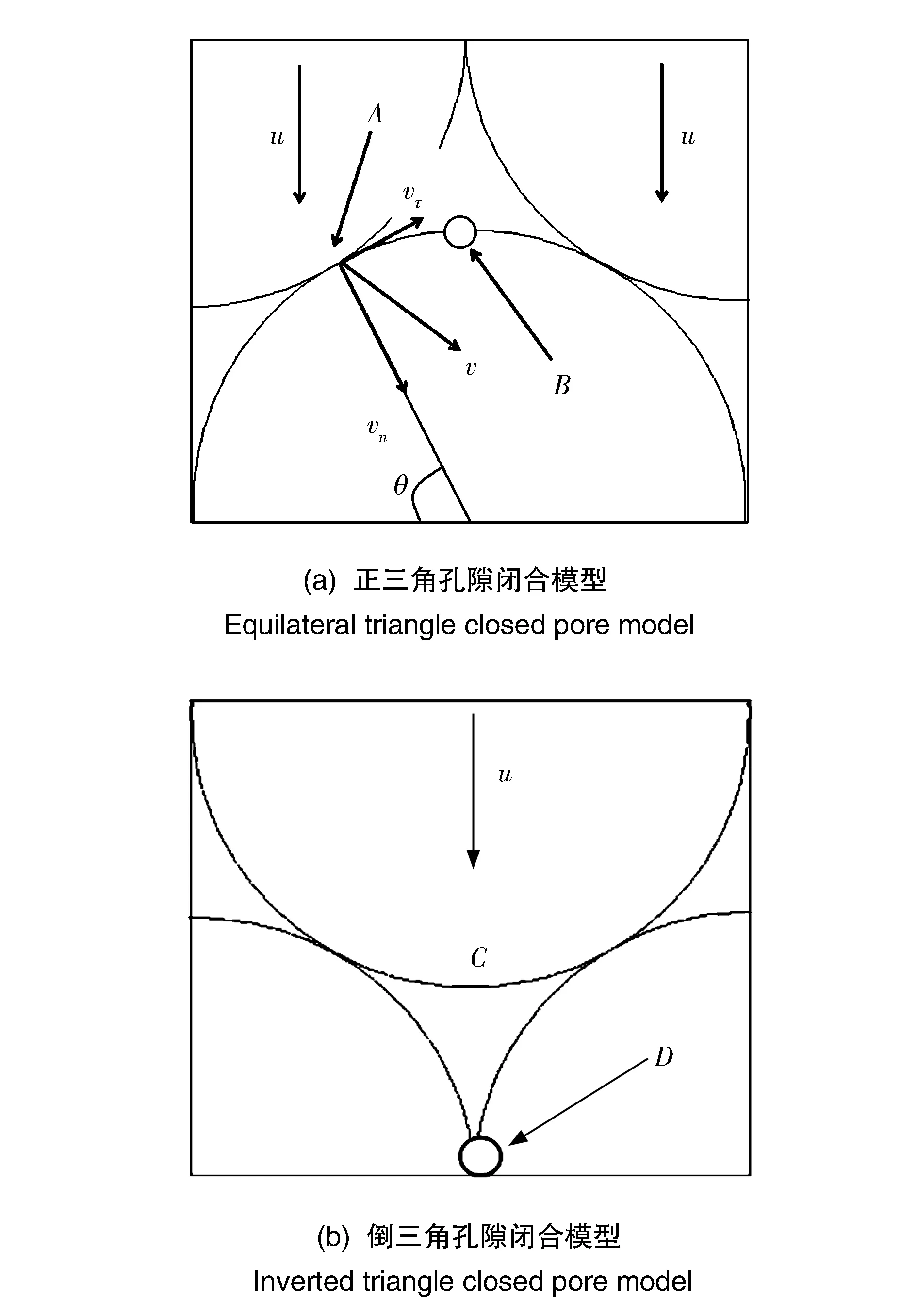
图2 孔隙闭合沉能机制Fig.2 Mechanism of pore closure energy deposition
3爆炸压实过程的数值模拟
3.1简化模型的建立
模拟与理论分析所选取的简化模型相同,如图2所示。颗粒半径取5 μm,模型上方施加的是速度边界条件,速度方向竖直向下。其他三个边界施加的是固定边界条件,速度分别取100 m/s和200 m/s。
3.2无氧铜的本构方程和状态方程
Johnson-Cook本构模型适用于大变形、高应变率及高温问题,广泛应用于爆炸、冲击、冲压成型等领域的数值模拟。Johnson-Cook本构方程形式如下所示〔14〕:
(1)
Hugoniot冲击关系为:
(2)
与冲击波关系ρ0D=ρ(D-u)、PH=ρ0Du联立,可以得到冲击压力的表达式:

(3)
无氧铜状态方程选用AUTODYN数据库的Shock状态方程,其中C1=3.958 km/s,S1=1.497,S2=0,S3=0,γ0=2。ρ0为材料的初始密度,μ为压缩度,μ=ρ/ρ0-1。
4结合沉能机制的爆炸压实孔隙闭合模拟分析
4.1正三角形孔隙闭合
图3为正三角形孔隙闭合。由文献〔15〕可知,铜的爆炸焊接流动限为1 365 m/s,声速限为3 910 m/s,焊接下限为183 m/s,由于颗粒尺寸仅为微米量级,可以不考虑焊接上限问题。由图3(a)、(b)可知,在孔隙闭合过程中,同排颗粒之间存在着爆炸焊接现象,并且产生的高速射流将强烈侵彻与之相邻的下排颗粒,产生侵彻沉能〔16〕。图3(c)为200 m/s下的应力分布图,可以看出,在孔隙闭合的过程中应力主要集中在射流尖端和上下颗粒接触面上。
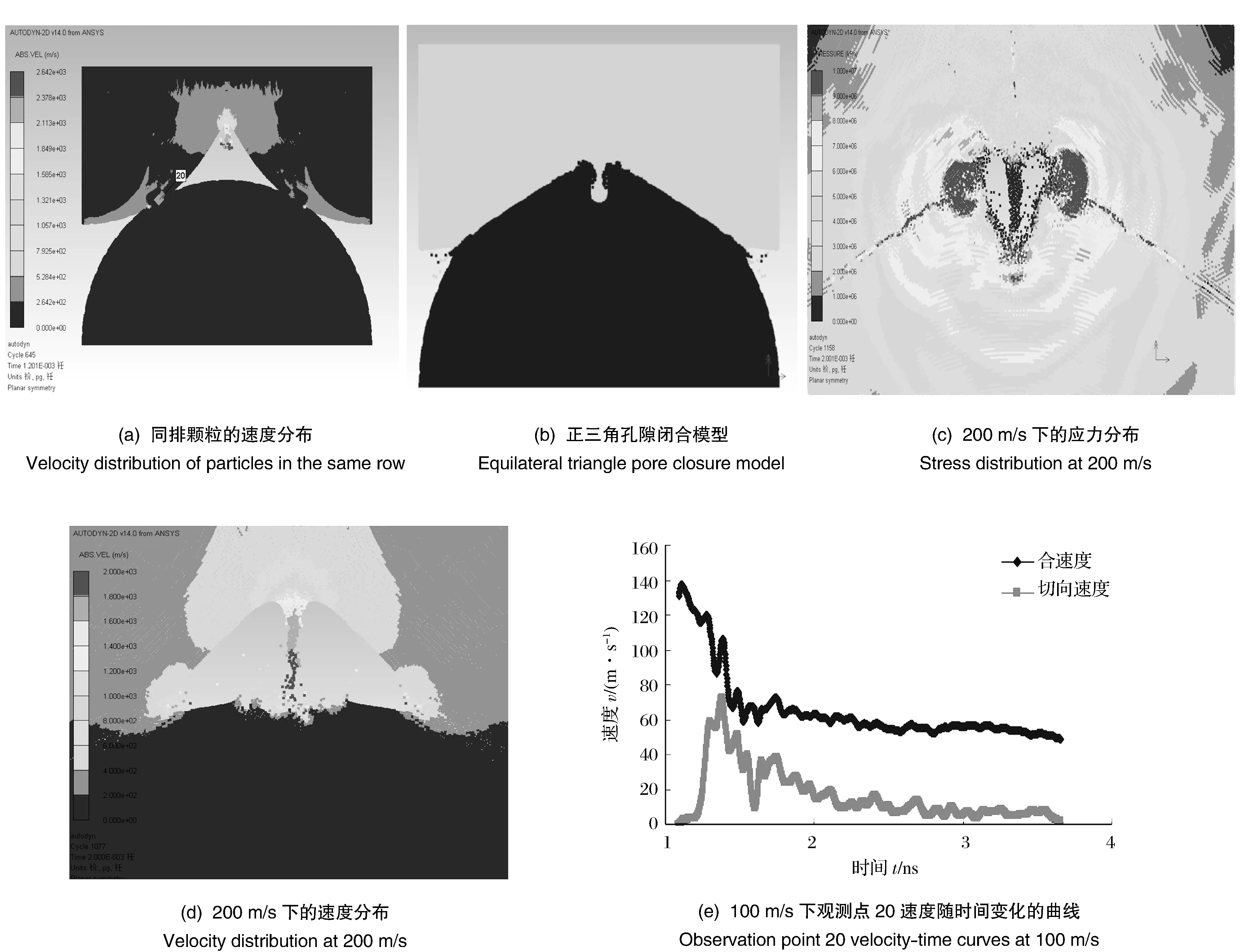
图3 正三角形孔隙闭合Fig.3 Regular triangle pore closure
由图3(d)中上下颗粒界面处的速度分布可知该处发生了微爆炸焊接。图3(e)是冲击速度为100 m/s时图3(a)中观测点20的速度时程曲线。由图3(e)中合速度曲线可知,碰撞速度没有达到爆炸焊接的下限,在碰撞点的切线方向上存在vτ,所以在此处附近发生的是微摩擦焊接。
4.2倒三角形孔隙闭合
图4为倒三角形孔隙闭合。从图4(a)可以看出,在孔隙闭合过程中,上排颗粒中间部分产生大的塑性变形,两侧产生射流侵彻下排颗粒,两侧是正三角形孔隙闭合的一部分。从图4(b)可以看出,孔隙闭合的过程中应力主要集中在颗粒接触面上。由图4(c)可知,上下排颗粒交界面上产生了微爆炸焊接。由图4(d)可知,该处同排颗粒间相互挤压速度比较小,该处的主要沉能机制为大塑性变形,随着挤压的加剧同排颗粒间产生微爆炸焊接。图4(e)是冲击速度为100 m/s时图4(a)中观测点22的速度时程曲线。分析方法与正三角形孔隙闭合时相同,在该区域附近产生的是冲击摩擦焊接。
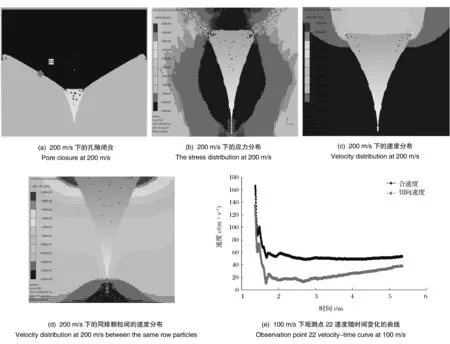
图4 倒三角形孔隙闭合Fig.4 Inverted triangle pore closure
5结论
(1)运用SPH方法对爆炸压实孔隙闭合过程进行数值模拟,得出了爆炸压实孔隙闭合过程出现的微爆炸焊接、微摩擦焊接、聚能射流以及大塑性变形等过程。
(2)正三角孔隙闭合时的沉能机制为:在同排颗粒的交界面上由于颗粒间的相互挤压而产生微爆炸焊接,并形成射流侵彻下排颗粒的顶部。在上下排颗粒的交界面上产生微爆炸焊接,当冲击的速度比较小时产生微摩擦焊接。与理论分析得出的正三角孔隙闭合爆炸压实沉能机制相符合。
(3)倒三角孔隙闭合时的沉能机制为:上排颗粒的大塑性变形,下排同排颗粒之间相互挤压产生的大塑性变形。上下排颗粒交界面上产生微爆炸焊接,当冲击的速度比较小时产生微摩擦焊接。与理论分析得出的倒三角孔隙闭合爆炸压实沉能机制相符合。
参考文献(References):
〔1〕 李晓杰,王金相,陈浩然,等. 金属粉末爆炸烧结颗粒间结合细观机制研究[J]. 应用基础与工程科学学报,2005,13(1):58-66.
LI Xiao-jie, WANG Jin-xiang, CHEN Hao-ran, et al.Research of microcosmic bonding mechanism of particles in explosive consolidation of metal powders[J]. Journal of Basic Science and Engineering,2005,13(1):58-66.
〔2〕 赵峥. 颗粒增强铜基复合材料的爆炸压实和数值模拟研究[D]. 大连:大连理工大学,2007.
ZHAO Zheng. Research on explosive compaction and numerical simulation of particle reinforced copper matrix composites[D]. Dalian:Dalian University of Technology, 2007.
〔3〕 NEMAT N S, OKINAKA T, NESTERENKO V. Experimental observation and computational simulation of dynamic void collapse in single crystal cooper[J]. Materials Science and Engineering: A, 1998, 249(1): 22-29.
〔4〕 COOPER S R, BENSON D J, NESTERENKO V F. A numerical exploration of the role of void geometry on void collapse and hot spot formation in ductile materials[J]. International Journal of Plasticity, 2000, 16(5): 525-540.
〔5〕TRAN L, UDAYKUMAR H S. A particle-levelset-b-ased sharp interface cartesian grid method for impact, penetration, and void collapse[J]. Journal of Computational Physics,2004,193(2):469-510.
〔6〕 赵铮,李晓杰,闫鸿浩,等. 爆炸压实过程中颗粒碰撞问题的SPH法数值模拟[J]. 高压物理学,2007,21(4): 373-378.
ZHAO Zheng, LI Xiao-Jie, YAN Hong-Hao, et al. Numerical simulation of particles impact in explosive-driven compaction process using SPH method[J]. Chinese Journal of High Pressure Physics,2007,21(4):373-378.
〔7〕 赵铮,李晓杰,陶钢. 冲击载荷下孔隙塌缩过程的数值模拟[J]. 爆炸与冲击,2009,29(3):67-72.
ZHAO Zheng, LI Xiao-jie, TAO Gang. Numerical simulation of the process of pore collapse under shockload[J].Explosion and Shock Waves,2009,29(3):67-72.
〔8〕 REAUGH J E. Computer simulations to study the explosive consolidation of powders into rods[J]. Journal of applied physics,1987,61(3):962-968.
〔9〕 REAUGH J E. Computer simulations of the explosive consolidation of powders[R]. Monterey, CA(USA):Lawrence Livermore National Lab., 1987.
〔10〕 张德良,王晓林. 粉末爆炸烧结材料参数效应数值研究[J]. 爆炸与冲击,1996,16(2):105-110.
ZHANG De-liang, WANG Xiao-lin. The numerical Research of the effect of material parameters on powder explosive consolidation[J]. Explosion and Shock Waves, 1996,16(2):105-110.
〔11〕 MURR L E, STAUDHAMMER K P, MEYERS M A.Metallurgical applications of shock wave and high strain rate phenomena[R]. New York: Marcel Dekker Inc., 1986.
〔12〕 MORRIS D G. Bonding processes during the dynamic compaction of metallic powders[J]. Materials Science and Engineering,1983,57(2):187-195.
〔13〕 邵丙璜,高举贤,李国豪. 金属粉末爆炸烧结界面能 量沉积机制[J]. 爆炸与冲击,1989,9(1):17-27.
SHAO Bing-huang, GAO Jv-xian, LI Guo-hao. The mechanism of energy deposition at the interface of metal powder in explosive consolidation[J]. Explosion and Shock Waves,1989,9 (1):17-27.
〔14〕 JOHNSON G R , COOK W H. Fracture character-istics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985,21(1):31-48.
〔15〕 李晓杰,杨温彬,奚进一,等. 双金属爆炸焊接下限[J].爆破器材,1999,28(3):22-26.
LI Xiao-jie, YANG Wen-bin, XI Jin-yi, et al. The Lower limit of explosive welding parameter window for bimetal[J]. Explosive Materials,1999,28(3):22-26.
〔16〕 史进伟,罗兴柏,刘国庆,等. 间隔介质对射流侵彻间隔靶影响的数值模拟[J]. 工程爆破,2015,21(5):19-22.
SHI Jin-wei, LUO Xing-bai, LIU Guo-qing, et al. Simulation on the influence of jet penetration by space medium of disconnected target[J]. Engineering Blasting,2015,21(5):19-22.
文章编号:1006-7051(2016)03-0001-05
收稿日期:2016-03-13
基金项目:国家自然科学基金面上项目(11272081)
作者简介:李晓杰(1963-),男,博士、教授,主要从事爆炸力学研究。E-mail: 18740280150@163.com
中图分类号:TD235.1
文献标识码:A
doi:10.3969/j.issn.1006-7051.2016.03.001
Explosive compaction pore collapse simulation based on SPH method
LI Xiao-jiea,b, CHEN Xianga, YAN Hong-haoa, WANG Xiao-honga, WANG Yu-xina
(a. Department of Engineering Mechanics, b. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, Liaoning, China)
ABSTRACT:SPH meshless numerical simulation method is suitable for studying large deformation problems. It has been a research focus in recent years. During explosive compaction, pore collapse plays a vital role on consolidation. AUTODYN software SPH method was used to simulate the process of explosive compaction. The model was simplified as equilateral triangle closed pore model and inverted triangle structure closed pore model in ball accumulation model. The material was copper powder, Johnson-Cook constitutive model,Hugoniot shock relations, and speed loading condition were adopted. Stress distribution velocity profile, large plastic deformation and velocity profile of collision point in the tangential were obtained by the numerical simulation. It indicated that micro-welding, micro-friction welding, high-speed jet and large plastic deformation existed in the process. The simulation results were consistent with the theoretical analysis.
KEY WORDS:Explosive compaction; SPH method; Pore collapse; Energy deposition mechanism; Numerical simulation

