基于Duffing混沌振子的微弱泥浆 脉冲信号提取研究

涂 兵，贺 燕， 许 艳， 李孝春，简 潇（1. 湖南理工学院 信息与通信工程学院，湖南 岳阳 414006； 2. 湖南理工学院 IIP创新实验室，湖南 岳阳 414006； 3. 湖南理工学院 复杂系统优化与控制湖南省普通高等学校重点实验室，湖南 岳阳 414006）

基于Duffing混沌振子的微弱泥浆 脉冲信号提取研究

涂 兵1，2，3，贺 燕1，2， 许 艳1，2，3， 李孝春1，2，简 潇1，2
（1. 湖南理工学院 信息与通信工程学院，湖南 岳阳 414006； 2. 湖南理工学院 IIP创新实验室，湖南 岳阳 414006； 3. 湖南理工学院 复杂系统优化与控制湖南省普通高等学校重点实验室，湖南 岳阳 414006）

针对无线随钻测量中泥浆脉冲信号信噪比大、有用信号提取难的问题，本文首先对泥浆脉冲信号的组成成份进行了分析，然后将Duffing混沌振子算法应用到了泥浆脉冲信号的提取上. 由于Duffing混沌振子算法具备对初值敏感、对噪声具有较好的抵抗力等优点，所以在检测微弱泥浆脉冲信号时能够表现出良好的效果，从而实现对微弱泥浆脉冲信号的提取. 该算法能满足工程应用的要求，可为泥浆脉冲信号提取提供新的思路.

泥浆脉冲信号； Duffing混沌振子； 信号提取

引言

在石油钻井过程中，微弱泥浆脉冲信号的提取容易受到各种因素的影响. 虽然无线随钻测量技术已得到广泛应用，但对于噪声的处理方法尚不完善，导致采集到的泥浆脉冲信号幅值小，且含有大量的噪声. 因此如何将微弱泥浆脉冲信号从强噪声背景下准确地提取出来是本文的主要研究内容. 自上世纪90年代开始，针对微弱泥浆脉冲信号的提取，国内进行了一系列的理论和实验研究. 苏义脑，张伟[3～9］等人详细分析了微弱泥浆脉冲信号以及噪声干扰源，为在强噪声背景下检测出有效信号，在无线随钻测量系统中运用了小波神经网络阈值去噪方法，并提出了一种基于高阶统计量的小波包抑制压力波噪声的新方法. 李传伟[10］等人为有效去除噪声，实现信号的提取，利用小波对信号进行变换，分析信号、噪声和基线的模极大值传播特性，为检测基线矫正和脉冲位置，提出了模极大值平方后与相邻系数相乘且归一化的处理方法. 赵建辉[11］等人针对采集到的微弱泥浆脉冲信号，提出了一种非线性“平顶消除”的方法，并对钻井液压力波脉位编码原理进行分析，得到其噪声及干扰的特点，采用线性滤波方法与非线性“平顶滤波”方式还原泥浆脉冲信号. 郑一等人[12］采用集合经验模态算法对泥浆压力波信号进行了信号的提取.

传统的线性滤波在检测信噪比很低的信号时效果很差. 混沌信号具有极强的“伪随机”性和“宽频”性，对噪声具有较好的抵抗力，因而在通信、信号检测、生物工程等诸多领域得到广泛应用. 本文首先对泥浆脉冲信号进行噪声分析，提出基于Duffing混沌振子的微弱泥浆脉冲信号的提取研究.

1 泥浆脉冲信号分析

井下条件复杂多变，地面采集系统采集到的钻井液脉冲信号受到各种噪声混杂及频率成分交错的影响，导致钻井液脉冲信号幅值小、噪声大，难以用单一的模型来表示，只能采用脉冲信号与杂波、噪声相统一的复合信号模型来分析钻井液脉冲信号[12］.

一般认为噪声信号为宽带白噪声，钻井液信号的数学模型可表示为：

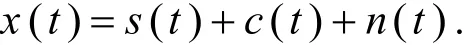
其中（）st表示井下数据编码的脉冲信号，（）ct表示周期性的泵冲信号，（）nt表示噪声信号. 如图1为一段泥浆脉冲信号原始波形，钻井液压力值波动范围为0.01～0.10MPa. 对泥浆脉冲原始信号进行频谱特性分析，运用数值仿真软件重点分析原始泥浆脉冲信号的组成成分以及不同的噪声信号叠加对泥浆压力波信号的影响. 图2为对泥浆脉冲原始信号进行频谱分析后的示意图，其中高频噪声和低频噪声在采集到的原始信号中占较大比例.

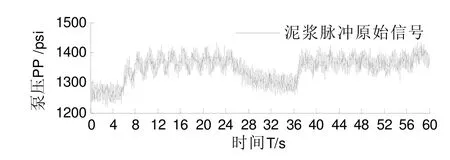
图1 泥浆脉冲原始信号

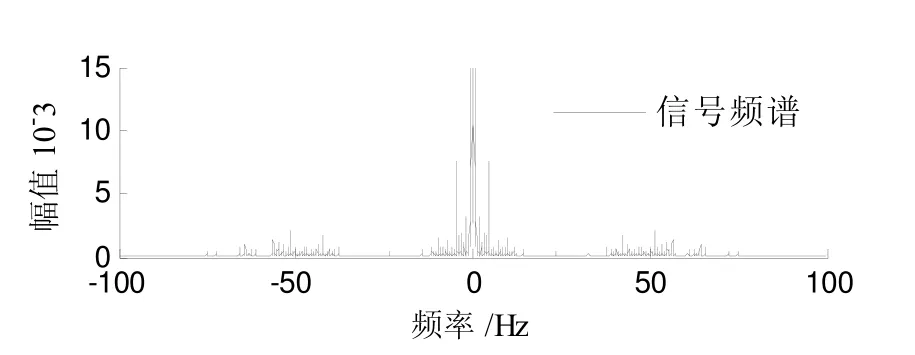
图2 泥浆脉冲信号频谱图

2 基于Duffing混沌振子的泥浆脉冲信号提取

2.1 Duffing混沌振子模型

Duffing振子检测系统由二阶微分方程组成，其具体形式为[13～15］

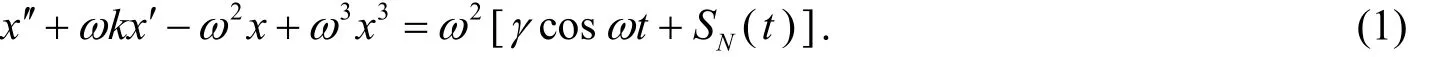
其中x为系统输出信号，ω为被测信号的角频率，k为阻尼系数，γ为内置激励信号幅值，SN（t）为输入信号，且

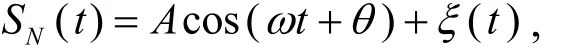
其中A为被测信号的幅值，θ为相位，ξ（t）为噪声.

本文主要利用相轨迹分析判别方法对Duffing混沌振子系统进行研究. Dulling混沌振子的输出状态对系统的激励信号幅度具有较强的敏感性. 随着系统的激励信号幅度的变化，Duffing混沌系统的输出状态表现出不同的相轨迹，主要表现为以下四种：

（1） 当信号输入即γs=0时，内置激励信号等于系统的激励信号，稳定状态时其相点的轨迹图有终止点；

（2） 当γs较小时，相轨迹点围绕焦点作周期振荡；

（3） 当γs超过系统阈值时，相轨迹如图3所示，系统将由周期分叉现象逐渐进入混沌状态，相平面中像点围绕两个焦点做周期运动；

（4） 当γs大于分岔值γd时，相轨迹如图4所示，系统由混沌状态进入大尺度周期状态，线性振子处于主导地位，相轨迹处于稳定状态.

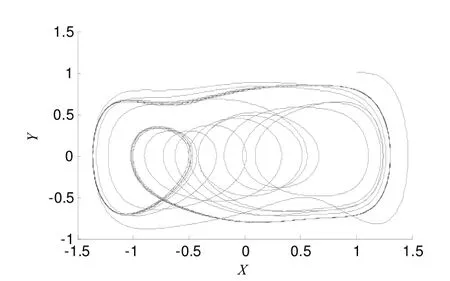
图3 混沌态相轨迹图

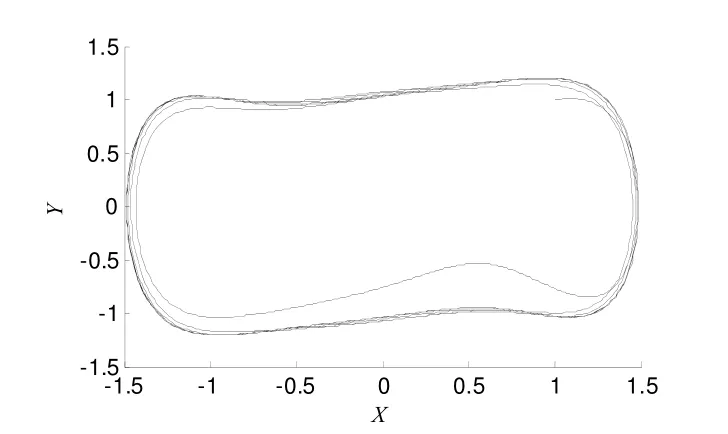
图4 周期态相轨迹图

2.2 Duffing混沌振子检测微弱信号

通过比较系统状态的不同变化，可以看出Duffing方程在混沌态和周期态的相轨迹图明显不同，可直接通过肉眼观察其变化，其对幅值的敏感性和变化具有直接可观察性，有利于提高微弱信号提取的信噪比. 因此将临界混沌到大尺度的相变作为判断的依据，可以实现信号的检测.

Duffing混沌振子检测微弱信号幅值的方法： 设混沌状态方程为s（t）=a0cosωt+n（t ），调节大尺度周期状态转变的临界值，使系统处于临界混沌状态； 改变系统参数，当策动力为Acosωt+a0cos ωt + n（t）时，相轨迹由临界状态调整为大周期状态，策动力的频率与待测信号的频率相等，微弱信号存在于系统的待测信号中； 最后，逐渐减少混沌系统中策动力的幅值，相轨迹由大周期状态改变为临界混沌状态，记录此时混沌系统的策动力，估计出周期信号的幅值.

当系统加入待测信号s（t）后，方程为

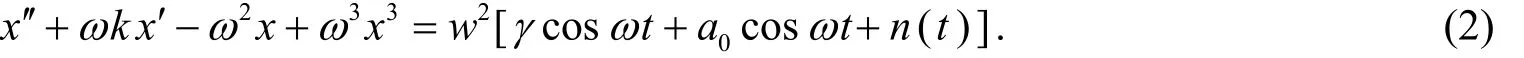
此时内置激励信号与微弱信号共同组成系统的激励信号，其幅值γs=，相位φ=arctan（Asinθ/（γ+Acosθ））. 其中内置激励信号的幅度远大于微弱信号的幅度A，逐渐增大策动力，系统输出将由混沌状态进入稳定的大周期状态.

2.3 Duffing混沌振子检测微弱信号仿真实验

对信号传输频率为0.5Hz曼彻斯特编码的泥浆信号进行仿真分析，泥浆脉冲信号的采样频率为200Hz，对Duffing混沌振子的初始值参数设置为a0=0.0025. 图5（a）为待测泥浆脉冲信号的时域图，截取60s时间内的一段信号，图5（b）为未输入信号时的相图，图5（c）为产生共振后检测出的泥浆脉冲信号时域图，图5（d）为输入检测信号后的相图.

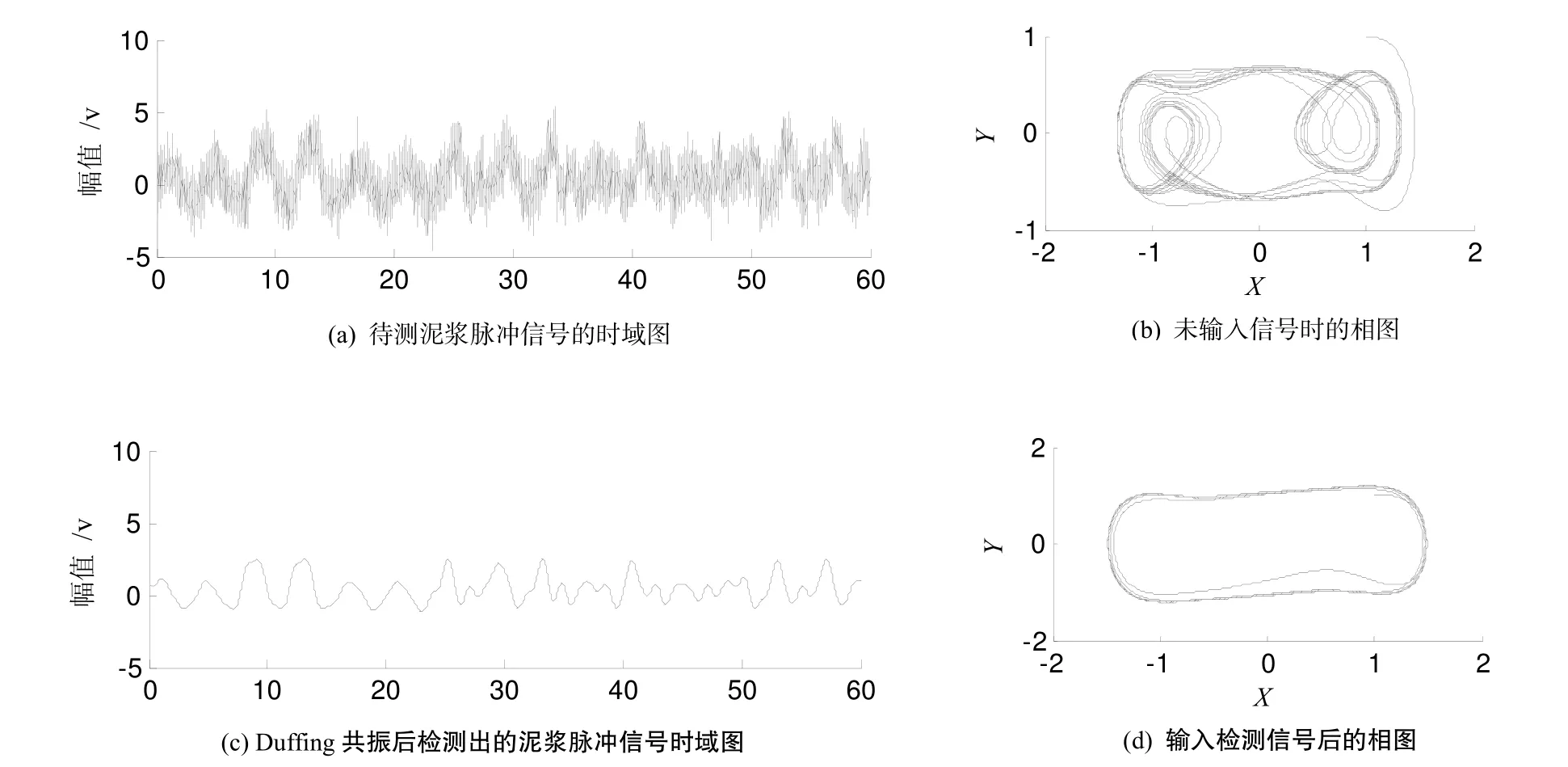
图5 泥浆脉冲波信号时、相图

3 结论

在工程中，噪声是不可避免的，而噪声的存在往往影响有用信息的提取. 本文对泥浆脉冲信号进行了噪声分析，传统的泥浆脉冲信号检测方法在检测信噪比很低的信号时效果很差，而Duffing振子混沌系统具备对初值敏感、对噪声的抵抗力较强等优点，因此本文将Duffing振子应用到微弱泥浆脉冲信号的检测. 通过仿真结果表明，该方法能为泥浆脉冲信号的检测提供新的思路，能符合工程应用要求.

[1]刘修善，苏义脑. 地面信号下传系统的方案设计[J[. 石油学报，2000，21（6）： 88～90

[2]刘修善. 钻井液脉冲沿井筒传输的多相流模拟技术[J[. 石油学报，2006，27（4）： 115～118

[3]Shen Yue，Su Yinao，Li Gensheng. Numerical modeling of DPSK pressure signals and their transmission characteristics in mud channels[J[. Petroleum Science，2009，6（3）： 266～270

[4]Wang J X，Liu H J. A time-frequency mixed method for on-line monitoring of harmonics and interharmonics[C[. APAP 2011： 228～233

[5]D.J.Zhao，B.J.Zhao，W Wang. Data processing techniques for a wireless data transmission application via mud[J[. EURASIP Journal on Adavances in Signal Proceesing，2011，1（45）： 1～8

[6]Fang Yuan，Xianfeng Gong. Research on signal processing of continuous wave mud pulse[C[. MACE，2011： 627～631

[7]刘 均，袁 峰. 钻柱内连续波信号传输模型与幅频特性研究[J[. 仪器仪表学报，2015，36（1）： 118～125

[8]张 伟，师奕兵，卢 涛. 无线随钻泥浆信号小波包去噪处理[J[. 电子测量与仪器学报，2010，24（1）： 80～84

[9]Wenyuan Chen，Bin Fang，Yi Wang. MWD Drilling Mud Signal De-noising and Signal Extraction Research Based on The Pulse-code Information，ICWAPR，2010，1： 244～249

[10]李传伟，李安宗. 一种小波变换信号处理方法[J[. 西安电子科技大学学报（自然科学版），2009，36（4）： 751～755

[11]Zhao Jianhui，Wang Liyan，LiFan. An Effective Approach for the Noise Removal of Mud Pulse Telemetry System[C[.ICEMI，2007，1： 971～973

[12]郑 一，孙晓峰，陈 健，等. 基于集合经验模态的随钻脉冲信号优良降噪算法[J[. 石油勘探与开发，2012，39（6）： 750～753

[13]李 月，杨宝俊，石要武，等. 基于混沌阵子检测淹没在强噪声中的方波信号[J[. 吉林大学自然科学学报，2001（2）： 13～17

[14]兀旦辉，李秦军，杨 萍. 噪声对基于Duffing方程弱信号检测的影响研究[J[. 计算机测量与控制，2010，18（1）： 61～63

[15]周 玲，田建生，刘铁军. Duffing混沌振子用于微弱信号检测的研究[J[. 系统工程与电子技术，2006，28（10）： 1477～1481

Research on Weak Mud Pulse Signal Extraction Algorithm Based on Duffing Chaotic Oscillator

TU Bing1，2，3，HE Yan1，2，XU Yan1，2，3，LI Xiao-chun1，2，JIAN Xiao1，2
（1. College of Information and Communication Engineering，Hunan Institute of Science and Technology，Yueyang 414006，China； 2. Laboratory of Intelligent-Image Information Processing，Hunan Institute of Science and Technology，Yueyang 414006，China； 3. Key Laboratory of Optimization and Control for Complex Systems，Hunan Institute of Science and Technology，Yueyang 414006，China）

Aiming at the problem of the noise ratio of mud pulse signal and the extraction of useful signal in wireless random drilling，in this paper，the signal components of mud pulse signal were analyzed，and the Duffing chaotic oscillator was also applied to the mud pulse signal. The simulation results showed that because of the Duffing chaotic oscillator algorithm is sensitive to the initial value and has good resistance to noise，which can show the good effect in the detection of weak mud pulse signal，so as to realize the extraction of weak pulse signal. This algorithm not only can meet the requirements of engineering applications，but also can provide a new idea for the mud pulse signal extraction.

mud pulse signal，Duffing chaotic oscillator，signal extraction

TM733，TM93

A

1672-5298（2016）02-0043-04

2016-02-18

2015年湖南省大学生研究性学习与创新性实验室计划项目（湘教通[2015[84号）

涂 兵（1983- ），男，湖南岳阳人，博士，湖南理工学院信息与通信工程学院讲师. 主要研究方向： 微弱信号处理、计算机视觉、智能信息处理