二阶非线性中立型时滞微分方程周期解的存在性

颜李朝，张映辉（. 湖南师范大学 数学系，长沙 4008； . 湖南理工学院 数学学院，湖南 岳阳 44006）

二阶非线性中立型时滞微分方程周期解的存在性

颜李朝1，张映辉2
（1. 湖南师范大学 数学系，长沙 410081； 2. 湖南理工学院 数学学院，湖南 岳阳 414006）

利用抽象连续定理，研究了一类二阶非线性中立型时滞微分方程周期解的存在性，给出了该方程存在周期解的充分性定理.

中立型时滞微分方程； 周期解； Fredholm算子

引言

含时滞的非线性微分系统周期解在控制论﹑金融学﹑生态学等领域有着广泛的应用，对其研究具有重要的理论与现实意义，引起了人们的广泛关注. 文[1～3[讨论了一阶非线性中立型时滞微分系统周期解的存在性，文[4～6[讨论了二阶非线性中立型时滞微分系统周期解的存在性. 其中，文[1，2[研究了一阶非线性时滞微分系统

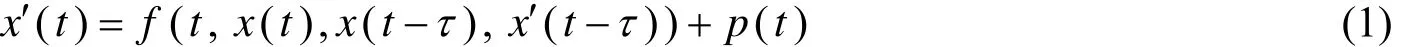
周期解的存在性，此方程的特点是非线性项中含有一阶导数. 受此启发，本文考虑二阶中立型方程

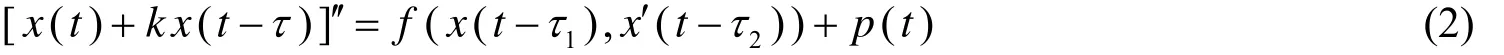
周期解的存在性. 其中k，τ，τ1，τ2为常量，τ≥0，τ1≥0，τ2≥0，|k|＜1，f∈C（ℝ2，ℝ），p∈C（ℝ，ℝ），p（t+T）=p（t ）并∫0Tp（t）dt=0. 与文[4～6[中研究的二阶非线性中立型系统不同，系统（2）中非线性项f含有一阶导函数. 这类系统在实际生活中有着更加广泛的应用.

1 记号与引理

为行文方便，引入一些记号：

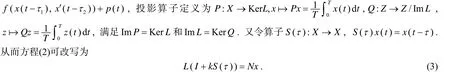
考虑如下对应方程

由于|k|＜1，可得H=I+kS（τ）为X的一个同胚，从而逆算子设y=Hx，由（3）和（4），有

故关于系统（3）的Mawhin连续定理可做如下表述：

（b） ∀x ∈∂Ω∩KerL，有QNx≠0且deg（QNx，Ω∩KerL，0）≠0. 那么，系统L（I+kS（τ））=Nx 在domL∩上至少存在一个解.

证明 因为L为指数是零的Fredholm算子，且H=I+kS（τ）为X的一个同胚，所以由已知N在Ω上L-紧得NH-1在H）上L-紧. 由条件（a），（b）可得

（B） ∀y∈∂（H（Ω））∩KerL，有QNH-1y≠0且deg（QNH-1y，H（Ω）∩KerL ，0）≠0.

从而根据Mawhin连续定理，可得系统Ly=NH-1y在domL∩H）上至少存在一个解. 又由domL=X，可知系统LHx=Nx在domL∩上至少存在一个解.

2 主要结果

定理1 假设满足如下条件：

为证明此定理，需先引入一条引理. 设

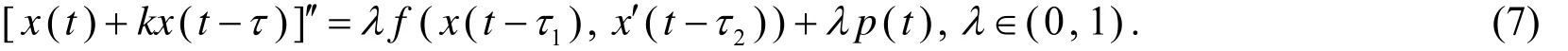
引理2 假设定理1中条件均满足，那么对于系统（7）的任一周期解x（t），存在与λ无关的正数Dj（j=0，1，2）使得

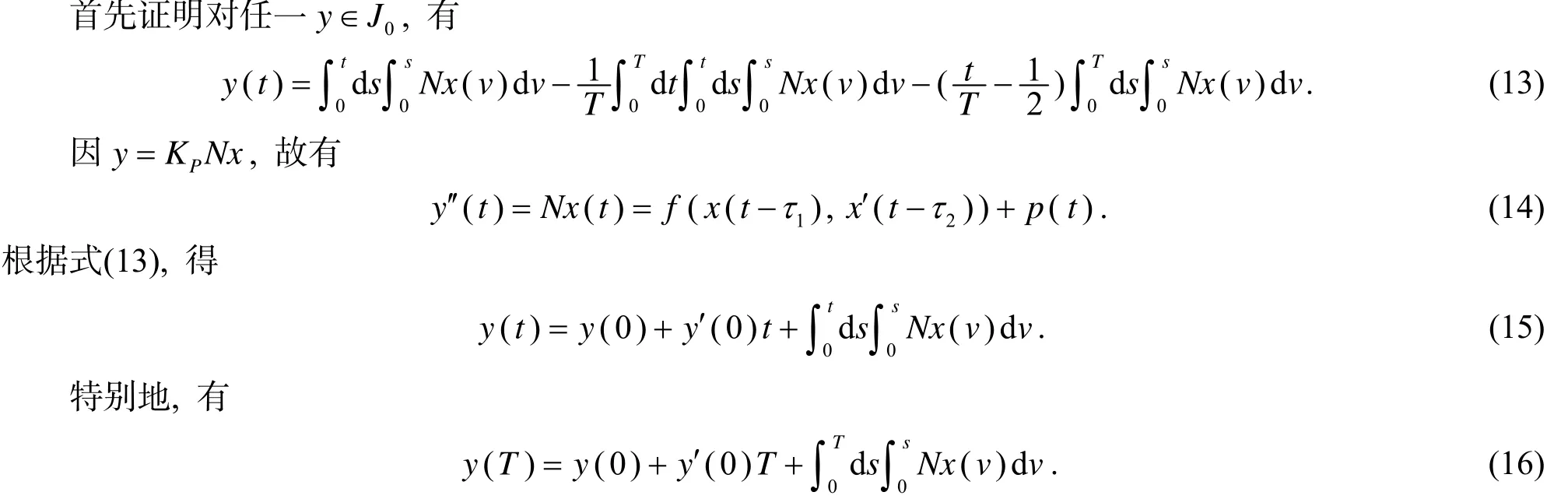
由于y（t）的周期为T，从而y（0）=y（T），则由式（15），可得

定理1的证明

根据PK的定义可得KeryP∈，于是

根据式（15）与（18），可得

根据式（19），得

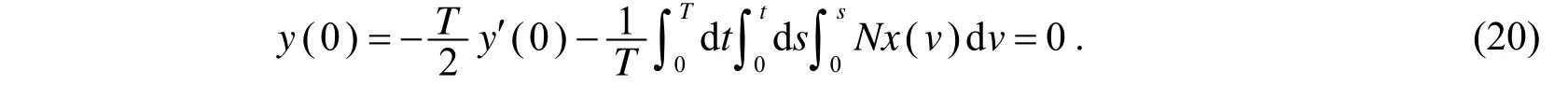
于是，由式（15），（17）与（20），得

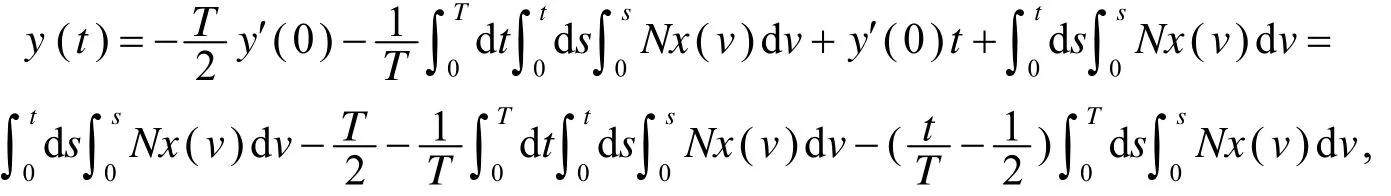
从而式（13）成立. 根据式（12）与（13）知

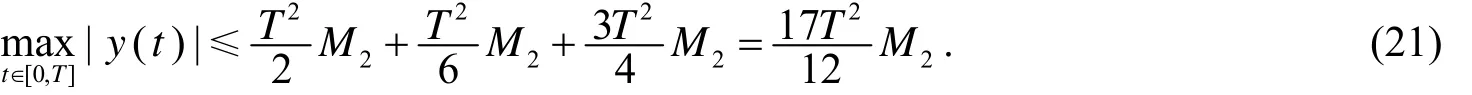
且根据式（13），对任给t∈[0，1[有

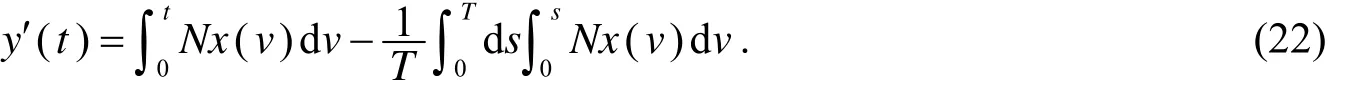
根据式（12）与（22），有

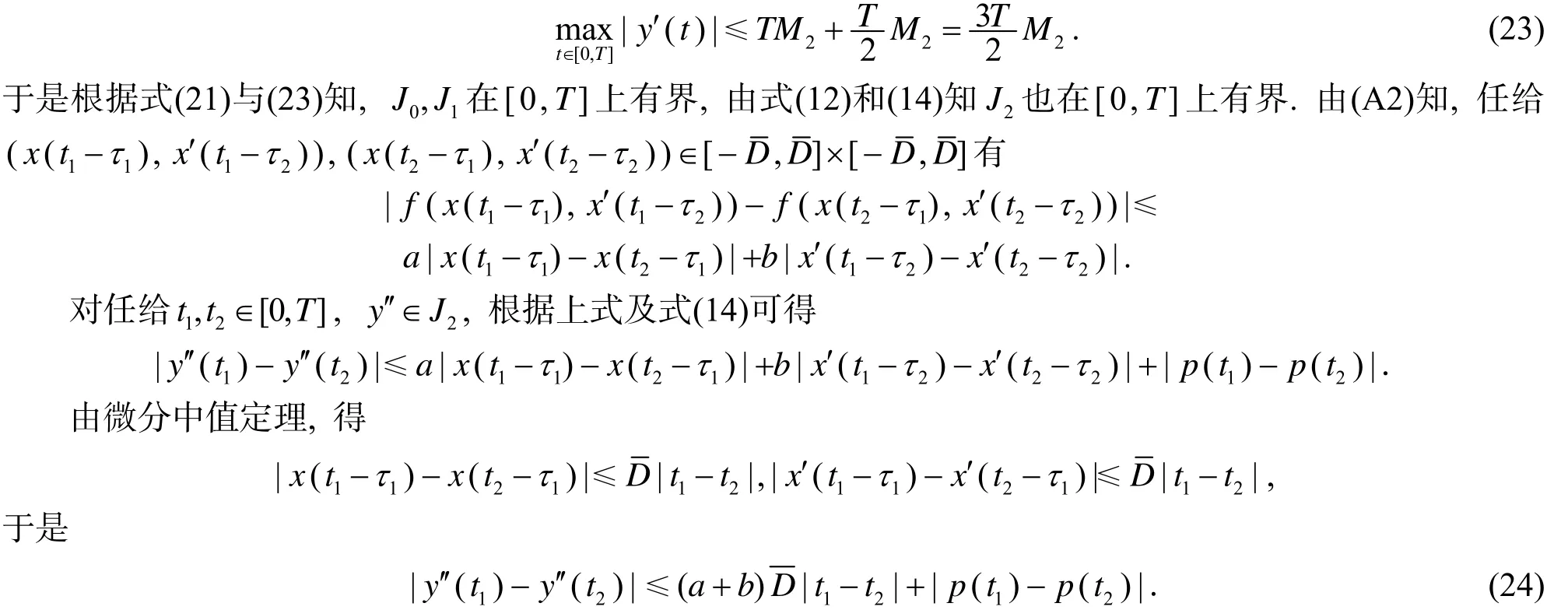
由p（t）的一致连续性，并结合式（24）可得J2在[0，T[上等度连续. 又根据微分中值定理及J2在[0，T[上的有界性可得J1在[0，T[上等度连续. 相应可推得J0在[0，T[上的等度连续性. 于是，J0，J1和J2均在[0，T[上有界并且等度连续，根据Arzela-Ascoli定理，可得K相对紧，从而KP（I-Q）N相对紧，所以N在L-紧.

根据引理得，任给λ∈（0，1）和x ∈∂Ω∩domL，有L（I+ks（τ））x≤λNx . 故引理1中条件（a）成立. 再证明条件（b）成立. 构造算子：

从而

于是得到引理1中条件（b）成立. 根据引理1得系统L（I+ks（τ））x=Nx 在上至少存在一个解 ，故系统（2）至少存在一个周期解.

定理2 假设|k|＜1 ，且满足条件：

（H1） τ1∈｛jT|j∈Z ｝；

（H2） 任给x∈ℝ且x≠0，y∈ℝ，有xf（x，y）＞0；

（H3） 存在a，b＞0，对于∀（x，y）∈ℝ×ℝ，有|f（x，y）|≤a|x|+b|y|，

则系统（2）至少存在一个周期解.

由（H2）及式（2）得

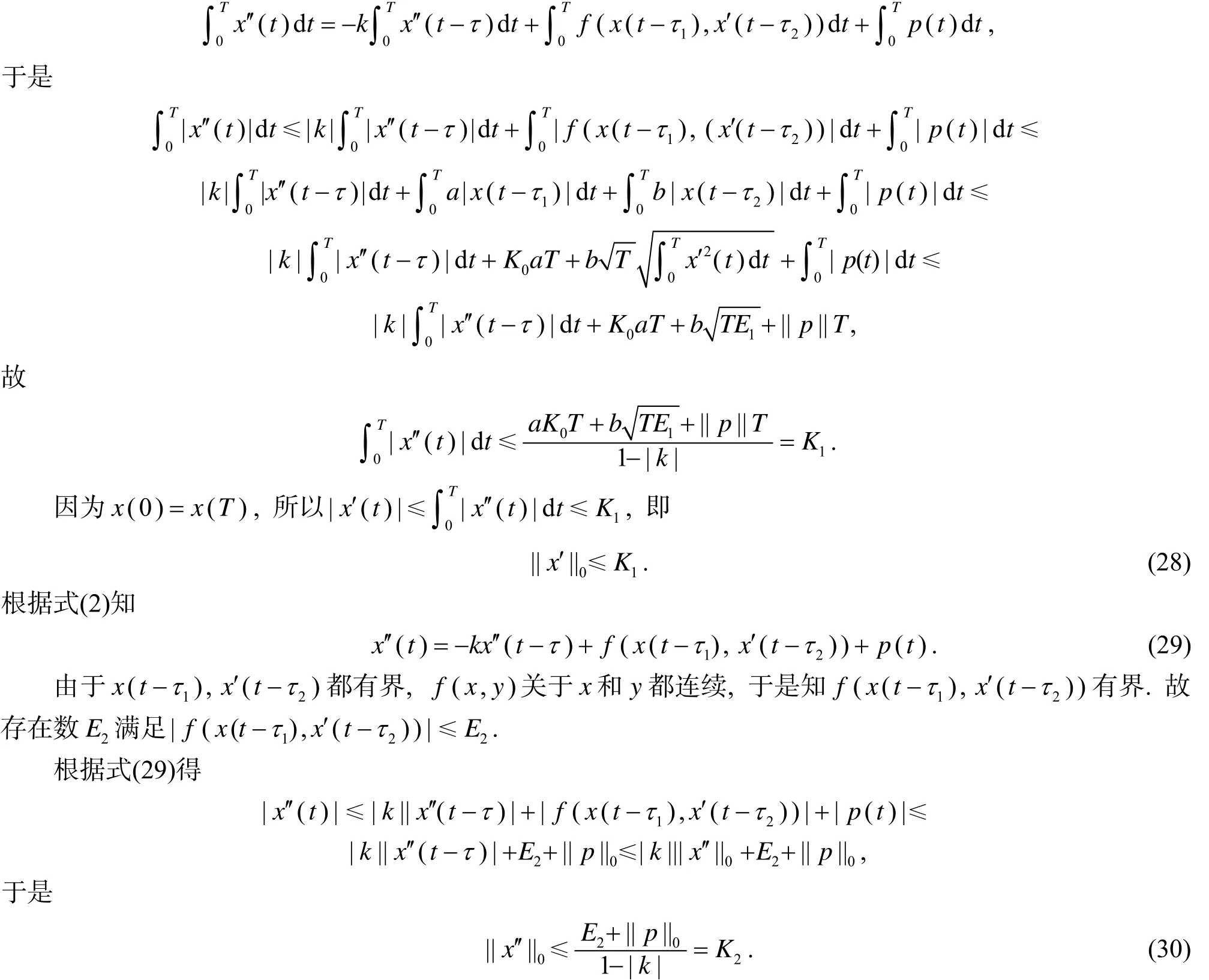
结合式（27），（28）与（30），知引理2条件满足.

类似定理1的证明，可以推知引理1中条件（a）成立.

现在只要证明条件（b）满足. 构造算子：

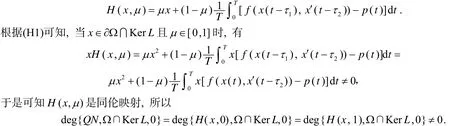
故知引理1的条件（b）满足. 故系统（2）至少存在一个周期解.

为说明上述结论的有效性并作为应用，给出一个例子.

例 考虑二阶非线性中立型时滞系统

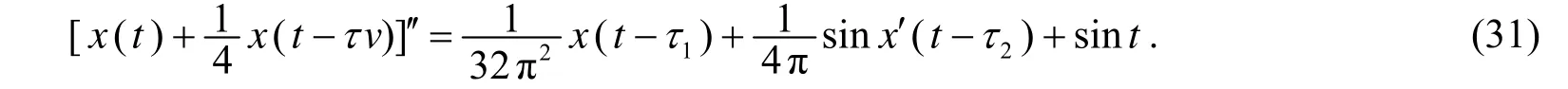
于是条件（A3）成立. 故时滞系统（31）至少存在一个2π周期解.

[1]任景莉，葛渭高. 一类非线性中立型时滞微分方程周期解的存在性[J[. 应用数学学报，2004，27（1）： 89～98

[2]刘 斌，庾建设. 一类非线性中立型时滞微分方程周期解的存在性[J[. 高校应用数学学报： A辑，2001，16（3）： 276～282

[3]Lu S.P.，Ge W.G.. On the existence of periodic solutions for neutral functional differential equation[J[. Nonlinear Analysis，2003，54： 1285～1306

[4]Guo C.J.，Guo Z.M.. Existence of multiple periodic solutions for a class of second order delay differential equations[J[. Nonlinear Analysis：RWA，2009，10（5）： 3285～3297

[5]Kuang Y.. Delay Differential Equations with Applications in Population Dynamics[M[. Academic Press，New York，1993

[6]Li Y.. Positive periodic solutions of nonlinear second order ordinary differential equations[J[. Acta Mathematica Sinica，2002，45（3）： 481～488

Periodic Solutions of Nonlinear Second Order Neutral Delay Differential Equation

YAN Li-zhao1， ZHANG Ying-hui2（1. College of Mathematics，Hunan Normal University，Changsha 410081，China； 2. College of Mathematics，Hunan Institute of Science and Technology，Yueyang 414006，China）

By using the abstract continuity theorem，we obained sufficient conditions for the existence of a periodic solution for a class of nonlinear second order neutral delay differential equation and gave a sufficiency theorem of a periodic solution.

neutral delay differential equation，periodic solution，Fredholm operator

O175.14

A

1672-5298（2016）02-0006-07

2016-02-16

国家自然科学基金项目（71501069）； 湖南省自然科学基金项目（2015JJ3090）

颜李朝（1981- ），男，湖南衡阳人，博士，湖南师范大学数学系讲师. 主要研究方向： 复杂动力系统及其应用