云南毛坪矿侧压系数与顶板破坏分析

张 涛，乔登攀，沐兴旺，马卓宇，黄 灏

(1. 昆明理工大学 国土资源工程学院，云南 昆明 650000； 2. 彝良驰宏矿业有限公司，云南 昭通 657000)



云南毛坪矿侧压系数与顶板破坏分析

张 涛1，乔登攀1，沐兴旺2，马卓宇2，黄 灏2

(1. 昆明理工大学 国土资源工程学院，云南 昆明 650000； 2. 彝良驰宏矿业有限公司，云南 昭通 657000)

采用RFPA2D模拟软件，采用应力加载方式，对不同侧压系数下的3 m×3 m矩形断面和3 m×5 m×5 m六角形断面进路进行数值模拟。研究云南彝良铅锌矿河东矿区毛坪矿760 m水平第五分层进路开挖时，3 m×3 m矩形断面进路和3 m×5 m×5 m六角形断面进路在不同的侧压系数下进路顶板及矿柱的破坏分析。两种巷围岩以剪切破坏为主，当侧压力系数为1.5 时，进路顶板突变破坏相对缓和。而侧压力系数为1.3时，充填体突变破坏较剧烈、破坏程度最大。随着侧压系数的增大,水平方向的位移会逐渐增大,垂直方向的位移会逐渐减小。侧压系数相同时，六角形断面的进路垂直位移比矩形断面的位移小，故在限制顶板位移方面明显优于矩形进路。

下向分层进路胶结充填采矿法；RFPA2D数值模拟；充填体；侧压系数

0 前 言

长期以来，人们对于下向分层进路胶结充填法采矿的进路稳定性分析，主要还是通过现场观测的总结[1-2]、室内外相似物理模型实验[3]和部分解析理论[4-5]来进行研究。近年来，在采场进路稳定性研究中，一些学者利用不同的数值模拟方法，已得到一些非常有价值的成果[6-8]。由于数值模拟方法能够考虑岩体的不同力学性质和变形特征，因而获得较为广泛的应用。但由于进路顶板破裂、移动、冒落和弯曲问题的复杂性,目前还没有一种数值模拟方法能够较全面地描述回采时充填体及矿柱的移动规律,包括充填体弯曲、脱层、破裂以及矿柱开裂、底板发生鼓起等全过程的动态模拟[9]。

本文以云南毛坪铅锌矿760 m中段第五分层的进路回采为研究对象，本文采用RFPA2D模拟软件，研究毛坪矿3 m×3 m矩形断面进路和3 m×5 m×5 m六角形断面在自重应力一定，不同侧压系数下顶板及矿柱的破坏方式及稳定性分析。对应不同的侧压系数，进行相应的施工方式，对安全回采作提前预判，减少事故的发生。

1 工程背景

毛坪铅锌矿位于云南省昭通市彝良县境内，采矿权属云南驰宏锌锗股份有限公司所有。目前矿山采矿作业主要集中在760 m和670 m中段Ⅰ号矿带处，主要采用机械化盘区下向分层水平进路胶结充填采矿法。下向分层进路胶结充填采矿法顶板为胶结充填体，深部高应力下回采，顶板的稳定性直接关系到整个回采过程的安全。进路顶板为上分层的胶结充填体，充填体自身的稳定性直接决定了下一分层回采的安全。

2 数值模型的建立与分析

本文所用RFPA2D系统，是一个能模拟岩石或充填体介质逐渐破坏过程的数值模拟工具，其基本原理参见文献[10-11]。RFPA2D包括应力分析和破坏分析两个方面的功能。考虑到岩石类脆性材料的抗拉强度远小于抗压强度，因此本文采用修正后的库伦准则(包括拉伸截断)作为单元破坏的强度判据，根据这一准则，单元的破坏可能是拉坏也可能是剪坏。该软件自开发以来应用广泛，许多学者使用该软件进行模拟所得结果较好[12-14]。

2.1模型的建立与参数选择

毛坪铅锌矿下向进路胶结充填法开采进路断面设计尺寸为3 m×3 m，上部结顶层厚度为1.5 m。充填体灰砂比为1∶8，下部为1∶4灰砂比的胶结体做充填体承载层，厚度为1.5 m。 3 m×5 m×5 m六角形进路承载层厚度为2.7 m，其接顶层厚度为2.3 m，灰砂比为1∶8。矩形3 m×3 m断面多条进路的模型宽37 m， 高24 m。六角形断面多条进路模型宽47 m，高为25 m。毛坪矿充填体及矿体力学参数如表1所示。

表1 毛坪矿充填体及矿体力学参数

将两个模型均划分为360×200个单元，数值模型中弹性模量和强度均服从Weibull 分布。矿体的最大压应变系数为95，最大拉应变系数为1.2。1∶4灰砂比充填体的最大压应变系数为60，最大拉应变系数为1.2，压拉比为5，设置加载100步。1∶8灰砂比充填体的最大压应变系数为50，最大拉应变系数为1.1，压拉比为4。图中的2号、4号、6号、8号为开挖进路。第3步时，对2号进路开挖。第5步时，对4号进路进行开挖。第7步时，对第6号进路进行开挖。第9步时，对8号进路进行开挖。该数值模型采用平面应变模型进行模拟分析，模拟中采用侧压加载控制。所建立的矩形断面进路和六角形断面进路模型如图1所示。

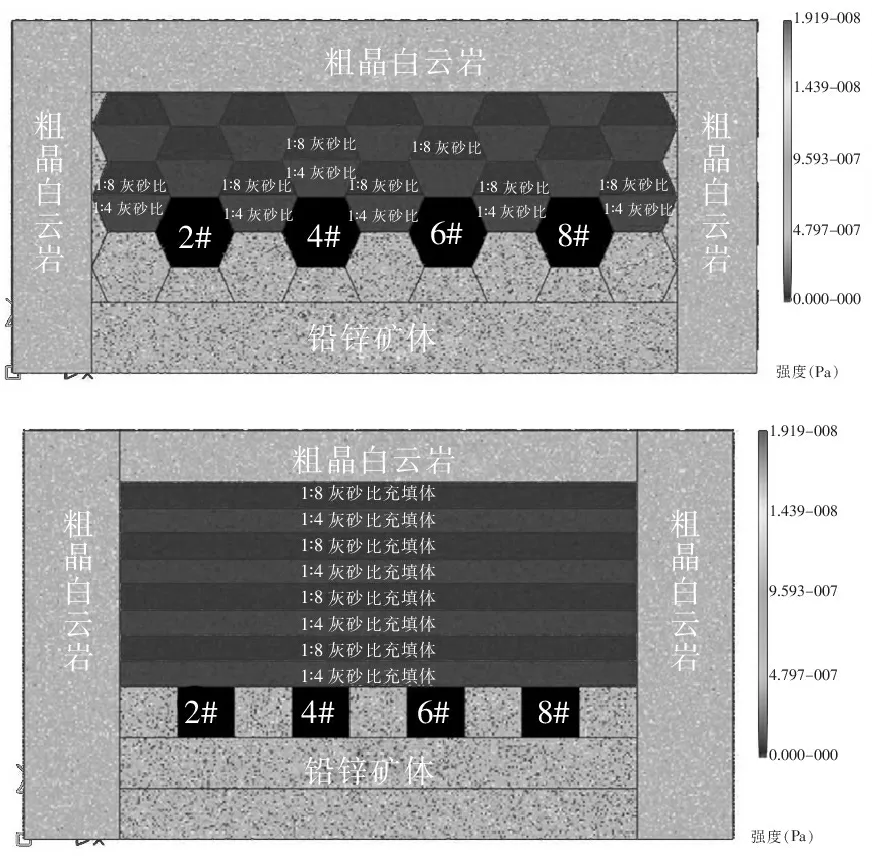
图1 计算模型

2.2应力加载取值分析

根据彝良铅锌矿河东矿区毛坪矿深部地应力规律测试及分析研究报告，760 m水平附近最大水平应力与自重应力的比值，最大一点为1.7倍，最小一点为1.29倍，平均为1.49倍。由于平硐口的标高为910 m水平，与760 m水平相距150 m。故通过计算得到自重应力为3 MPa，由于侧压系数 为1.29～1.7，故选取侧压系数为1.3、1.5、1.7分别对两种断面进而对其进行数值模拟计算。

3 计算结果分析

3.1 3 m×3 m矩形进路稳定性分析

通过模拟计算结果得到不同侧压系数下矩形断面进路X、Y向位移与加载步曲线如图2～3所示。

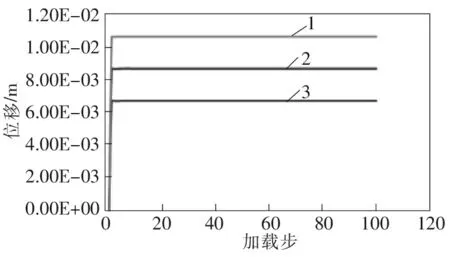
1 侧压系数为1.3； 2 侧压系数为1.5； 3 侧压系数为1.7

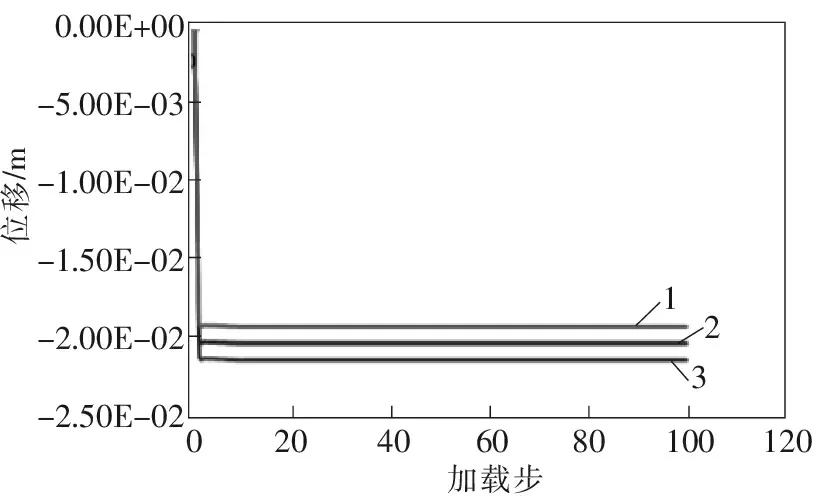
1 侧压系数为1.3； 2 侧压系数为1.5； 3 侧压系数为1.7

3.1.1 方案1

当侧压系数为1.3时，围压为3.9 MPa，最大主应力云图如图4所示。

图4 最大主应力云图

从图4看出：当第9步四条进路均开挖后，各条进路均稳定性良好，无明显的脱层、冒顶和片帮等现象。同时可以看出，进路开挖后，拉应力产生于矩形进路的顶板和底板的四个角落两侧，压应力产生于顶板中间位置，矿柱整体拉应力集中。由图2～3位移与加载步曲线可以看出：X向的最大位移为6.7 mm，Y方向的最大位移为19.1 mm。

3.1.2 方案2

当侧压系数为1.5时，围压为4.5 MPa，最大主应力云图如图5所示。

图5 最大主应力云图

从图5看出：当第9步四条进路均开挖后，各条进路均稳定性良好。由图2和图3位移与加载步曲线可以看出：X向的最大位移为8.6 mm，Y方向的最大位移为21.3 mm。随着应力的持续加载，水平方向和垂直方向均无位移的增加，充填体强度富余。

3.1.3 方案3

当侧压系数为1.7时，围压为5.1 MPa，最大主应力云图如图6所示。

图6 最大主应力云图

从图6看出：当第9步四条进路均开挖后，各条进路均稳定性良好。由图2～3位移与加载步曲线可以看出：X向的最大位移为10.6 mm，Y方向的最大位移为19.1 mm。随着应力的持续加载，水平方向和垂直方向均无位移的增加。

3.1.4 小结

1) 当顶部均布荷载为3 MPa时，分别选取了侧压系数为1.3、1.5、1.7对矩形断面进路进行了数值模拟。此种情况下，充填体假顶局部无分层脱落、开裂。

2) 随着侧压系数的增加，矩形进路的横向位移逐渐增大，竖直方向的位移在逐渐减小。即随着侧压系数的增大，假顶弯曲和下沉量变小。

3) 对于矩形3 m×3 m断面的进路而言，现有充填体强度足够富余，无须进行支护。

3.2 3 m×5 m×5 m的六角形进路稳定性分析

下向胶结充填六边形进路采矿方法采用仿生学原理，将进路断面设计为六边形断面，使采空区混凝土充填体呈蜂窝状镶嵌结构，从而改变其受力状况，提高稳定性。通过模拟计算结果得到不同侧压系数下六角形断面进路X、Y向位移与加载步曲线，见图7～8。

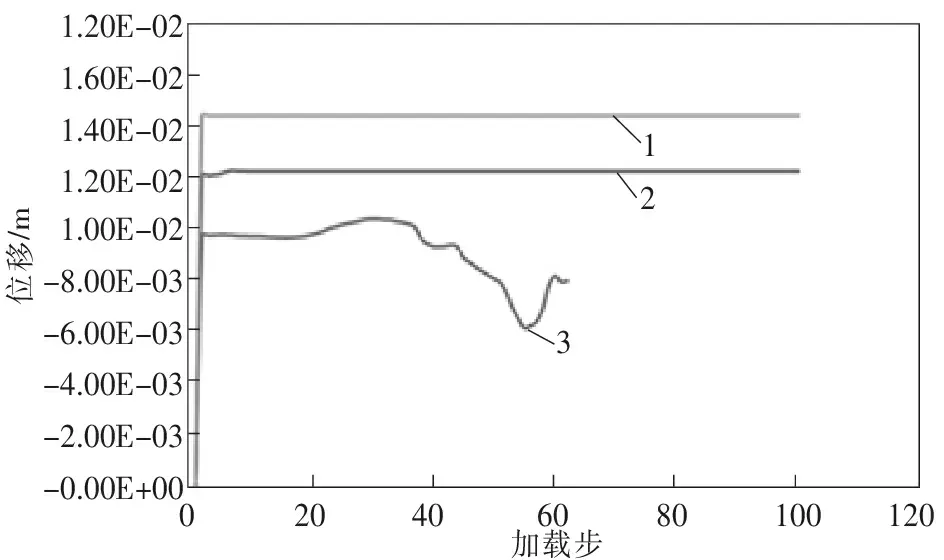
1 侧压系数为1.3； 2 侧压系数为1.5； 3 侧压系数为1.7

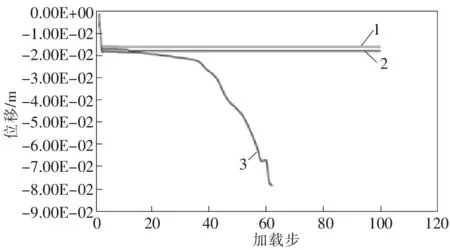
1 侧压系数为1.3； 2 侧压系数为1.5； 3 侧压系数为1.7

3.2.1 方案1

当侧压系数为1.3时，围压为3.9 MPa，最大主应力云图如图9所示。

图9 最大主应力云图

从图9可以看出：当第5步2号进路开挖后，进路左边的灰帮出现少量的片帮，第9步四条进路开挖完毕。随着应力的持续加载，第17步时4号进路的右手帮产生较大的裂缝，产生片帮。同时，6号进路的左手灰帮也产生裂缝和少量的片帮。第30步时，6号进路的右手帮灰体也产生大裂缝，4号和6号进路两帮的裂缝迅速向上贯通。第50步时，3号矿柱上的灰体劈裂破坏，第62步时，之前产生的裂缝相互贯通，帮上部开始出现与帮中部裂隙近乎垂直同时与帮下部裂隙方向一致的裂隙并与顶板裂隙相连，进而整体失稳。由图7中X方向的位移与加载步曲线可以看出：从第2步开始发生水平形变到36步，位移量从9 mm先逐渐增至10.4 mm，第36步开始，水平位移逐渐稳定。由Y方向的位移与加载步曲线可以看出，由于充填体受压，竖直方向位移从第3步开始随着2号进路的开挖，发生了1.7 mm的整体下沉，4号进路开挖后，位移量为17.9 mm，直至8号进路开挖后发生了18.1mm的位移。当四条进路全部开挖后，随着应力的持续加载，伴随着顶板脱层或顶板的弯曲下沉，以及矿柱开裂。破坏时垂直方向的最大位移为21.2 mm，充填体破坏后的垂直方向的最大位移为78.3 mm。因此，在第30步的时候及时的进行支护或者对采空的进路及时充填可有效防止采场下沉和垮塌。

3.2.2 方案2

当侧压系数为1.5时，围压为4.5 Mpa，最大主应力云图如图10所示。

从图10看出：开挖后顶板完整，无脱层，两帮也无片帮。侧压系数为1.5时，进路顶板和两帮稳定性最好。拉应力产生于六边形进路的顶端位置，压应力产生于两侧位置，中间两个拐点处应力集中现象明显。但拉应力值不大，未达到破坏状态。由图7中X方向的位移与加载步曲线可以看出：从第2步开始发生水平形变，位移量最大为12.3 mm。由Y向位移与加载步曲线可以看出，从第2步开始发生水平形变，竖向位移最大为17.3 mm。4条进路的开挖后，竖直方向和水平方向的位移均没有进一步增大。

图10 最大主应力云图

3.2.3 方案3

当侧压系数为1.7时，围压为5.1 MPa，最大主应力云图如图11所示。

图11 最大主应力云图

从图11看出：随着2号、4号、6号进路的开挖后，8号进路底板应力集中。当8号进路开挖后，第9步可以看到8号进路底板发生鼓起，受到水平应力的作用，鼓起的部分发生剪切破坏。顶板处于受拉状态。然而4条进路的顶板和矿柱均结构完整，稳定性良好。由图7中X方向的位移与加载步曲线可以看出：从第2步开始发生水平形变，位移量最大为14.5 mm。由Y向位移与加载步曲线可以看出，竖向位移最大为15.5 mm。

3.2.4 小结

1) 顶压为3 MPa，侧压系数为1.3，当开挖后，如果看到顶板脱层或者有明显的弯曲下沉，或者矿柱开裂严重，就应及时的对采场进行支护或对采空的进路及时充填。

2) 当顶压为3 MPa，侧压系数为1.5和1.7时，进路顶板完整，矿柱也没有裂缝。但当侧压系数为1.7时，底板有少量的鼓起，但不影响进路的稳定。

3) 随着侧压系数的增大，六角形水平位移增大，垂直方向的位移在逐渐减小。

4 结 论

通过运用岩石破裂过程分析系统(RFPA2D)，对彝良毛坪矿下向分层水平进路充填采矿法不同侧压系数开挖下的顶板破坏规律进行数值分析。初步可以得出以下结论。

1) 通过数值模拟的结果来看对于3 m×5 m×5 m六角形断面和3 m×3 m矩形断面而言，无论是六边形进路式、矩形进路式，两种断面进路都可以安全的对矿体进行开采。当侧压系数为1.3时，竖直位移量是最大的，水平位移量为最小。此时，围岩突变破坏较剧烈、破坏程度最大。

2) 从位移与加载步的曲线分析结果来看，在进路未发生破坏时，相同的侧压系数下，六角形断面进路的垂直位移量要比矩形断面的进路小。因此，六角形断面的进路在限制顶板位移方面明显优于矩形进路。

3) 在现有充填体强度和地应力条件下，完全可以将3 m×3 m的矩形进路用3 m×5 m×5 m的六角形断面替代，随着开采深的增加，六角形断面的结构优势将更加明显。

4) 充填体假顶与侧壁交接处应力集中是导致充填体顶板失稳的重要诱因，该处受拉伸或剪切破坏，其充填体的破坏先从顶板两侧逐渐向顶板中央逐渐贯通，导致承载层进一步下沉变形，加剧承载层中心点受拉破坏。矿柱与充填体接触处存在多条交错的剪切滑移裂缝逐渐贯通，是使进路顶板破坏失稳的主要原因。

[1] 郭生. 大断层影响下的巷道围岩变形破坏研究[J]. 煤炭科学技术, 2013(S2): 145-149.

[2] 刘高, 聂德新, 韩文峰. 高应力软岩巷道围岩变形破坏研究[J]. 岩石力学与工程学报, 2000(6): 726-730.

[3] 任智敏, 胡耀青. 大断面矩形和六边形煤巷围岩变形破坏试验对比研究[J]. 煤矿开采, 2014(3): 29-32.

[4] 何书, 赵奎. 下向进路侧帮可动块体的稳定性力学分析[J]. 金属矿山, 2012(12): 5-13.

[5] 任智敏. 基于尖点突变理论的大跨度巷道顶板稳定性分析[J]. 中国矿业, 2014(10): 111-114.

[6] 卫志强, 任智敏, 王树祥. 大断面回采巷道稳定性数值模拟研究[J]. 爆破, 2012(3): 42-77.

[7] 孟庆彬, 韩立军, 乔卫国, 等. 深部高应力软岩巷道变形破坏特性研究[J]. 采矿与安全工程学报, 2012(4): 481-486.

[8] 张广超, 何富连. 深井高应力软岩巷道围岩变形破坏机制及控制[J]. 采矿与安全工程学报, 2015(4): 571-577.

[9] 唐春安, 徐曾和, 徐小荷. 岩石破裂过程分析RFPA～(2D)系统在采场上覆岩层移动规律研究中的应用[J]. 辽宁工程技术大学学报(自然科学版), 1999(5): 456-458.

[10] Tang C A. Numerical simulation of progressive rock failure and associated seismicity. International Journal of Rock Mechanics and Mining Sciences, 1997.

[11] Tang C A. A new approach to numerical method of modeling geological processes and rock engineering problems. Engineering Geology, 1998.

[12] 钟波波, 张永彬, 李宏. 基于RFPA～(2D)的岩石裂纹扩展模式的研究[J]. 武汉理工大学学报, 2014(2): 82-88.

[13] 付斌, 周宗红, 王友新, 等. 煤岩组合体破坏过程RFPA～(2D)数值模拟[J]. 大连理工大学学报, 2016(2): 132-139.

[14] 刘俊杰, 陈雄, 张后全, 等. 运用RFPA～(2D)数值模拟开采条件下的渗流通道[J]. 岩石力学与工程学报, 2005(9): 1522-1526.

TheRoofFailureProcessAnalysisofLateralPressureCoefficientinMaopingMine

ZHANG Tao1, QIAO Dengpan1, MU Xingwang2, MA Zhuoyu2, HUANG Hao2

(1.KunmingUniversityofScienceandTechnologyLandResourcesEngineeringCollege,Kunming,Yunnan650000,China; 2.YiliangchihongMiningCo.,Ltd.,Zhaotong,Yunnan657000,China)

This paper uses RFPA2D simulation software in a loading method to simulate under different lateral pressure coefficients of 3 m×3 m rectangular and hexagonal section 3 m×5 m×5 m approach. The research on Yiliang Lead-zinc Mine with 760 m deep level in fifth slicing drift excavation shows that an analysis of 3 m×3 m rectangular cross-section approach and 3 m×5 m×5 m hexagon drift is under different lateral pressure coefficients in the route the roof and pillar damage. Two kinds of roadway surrounding rock are mainly shear failure when the lateral pressure coefficient is 1.5 with drift roof mutations disrupt in relative ease. The lateral pressure coefficient is 1.3, with filling mutations disrupt in more severe damage. In the development of lateral pressure coefficient, the displacement in the horizontal direction will gradually increase. Meanwhile the vertical displacement will decrease gradually. Lateral pressure coefficient is the same, with the hexagonal section of the route vertical displacement more than the displacement of the rectangular section of small. So in limit the roof displacement, it was significantly better than that of the rectangular approach.

Underhand cemented filling mining method; RFPA2D numerical simulation; Backfill; Lateral pressure coefficient

2016-09-03

国家自然科学基金项目(51164016)；甘肃省科技重大专项计划项目(1203GKDC003)

张涛(1990-)，男，甘肃兰州人，在读硕士研究生，研究方向：采矿工艺及理论，手机：18468069972，E-mail:651727568@qq.com；通讯作者：乔登攀(1969-)，男，甘肃白银市人，教授，博士生导师，研究方向：采矿工艺及理论，E-mail:1215550723@qq.com.

TD322

：Adoi：10.14101/j.cnki.issn.1002-4336.2016.04.016