传统矿柱安全系数计算公式优化研究①

黄 敏， Kulatilake P H S W， 罗嗣海， 方偏桃， 赵聪聪

（1.江西理工大学 资源与环境工程学院，江西 赣州341000； 2.长沙矿山研究院有限责任公司，湖南 长沙410012； 3.金属矿山安全技术国家重点实验室，湖南 长沙410012； 4.亚利桑那大学 岩体模拟与计算力学实验室，美国 亚利桑那州 图森85721）

矿产资源的地下开采是一个长期的过程，在采掘生产过程中，许多矿山形成了大量的采空区。 据2015年长沙矿山研究院有限责任公司对全国4 606 家地下非煤矿山的统计调查表明，超过50%的地下非煤矿山以空场法进行采矿，形成采空区规模约12.8 亿立方米，其中未经处理的空区约占80%。 大量未处理的采空区危害着矿山的后续开采，采空区诱发的冒顶、片帮等事故屡见不鲜，更有甚者引发大面积坍塌、岩移，直至地表塌陷，时刻威胁着矿山工作人员的生命及财产安全，采空区灾害已经成为我国分布最广泛、且危害最大的矿山灾害类型之一［1-3］。 而对于如此巨大的空区体积，短期内不可能全部完成治理。 因此，为缓解空区治理压力，同时确保井下生产安全，对采空区进行稳定性分析十分必要。 对于空场法开采的矿山，顶板与矿柱是维持地下空区稳定的两大结构单元，国内外学者对于空区的稳定性研究也主要针对这两方面展开。 对于顶板较为稳固的空区，矿柱的稳定与否更是对空区的支撑有着决定性作用。 矿柱不仅用于维护矿房的稳定，也用于隔离大面积空场，同时还肩负着保护井巷、地表及建筑物的安全作用。 为了保持采场长时间的稳定状态，保证井下生产工作的安全有序进行，在进行开采设计时，相邻矿柱的间距必须保证在顶板极限跨度之下，矿柱本身的横断面尺寸也必须满足强度要求［4］，以免因矿柱尺寸太小而无法承受其上覆荷载，导致矿柱被压垮。 矿柱一旦被压垮，其上覆岩层荷载将重新分布，该矿柱所承载的岩层质量将由其相邻的其他矿柱来承担。 因此，本文主要针对矿柱稳定性展开深入研究，可为类似工程提供技术参考。

1 矿柱稳定性研究现状

早期对采空区稳定性的研究主要靠矿山工作人员的经验积累，近年来，随着岩石力学研究不断深入和科学技术发展，特别是现代检测手段及计算机模拟分析技术被广泛应用于空区稳定性研究，并取得了良好效果，极大地丰富了关于空区稳定性的理论研究与工程实践［5］。 矿柱稳定性主要取决于矿柱自身强度和矿柱所承受的上覆岩层荷载。 对矿柱稳定性进行分析，其关键是对矿柱自身强度和上覆岩层荷载的正确计算［6-8］。 经过长时间的发展，国内外众多学者在这一方面作了许多研究，并总结了相关理论，包括压力拱理论、概率密度函数法、两区约束理论和面积承载理论等，同时在大量室内实验和工程实践的基础上，得到了多种关于矿柱强度的计算公式，主要有安全系数法、理论分析法、数值模拟法等。 其中，安全系数法能定量地对矿柱稳定性进行评价，且简单实用，因此被广泛应用于工程实际。

1.1 矿柱所受荷载

矿柱的平均应力取决于在单位面积内矿柱所承受的荷载。 国内外对于矿柱荷载的研究由来已久，也提出了多种假设与理论，目前具有代表性的主要有普氏平衡拱理论、有效区域理论、两区约束理论及面积承载理论等。

1.1.1 普氏平衡拱理论

普氏平衡拱理论基于自然平衡拱存在，坑道开挖过后，在无支护措施的情况下，坑道顶部会发生岩体自然冒落现象，直至形成一个短时间内保持相对平衡的拱形，称为平衡拱。

基于普氏拱的矿柱的承载机理如图1 所示。 岩体开挖后，采空区内的承压矿柱受到上覆岩层施加的自重应力，顶板岩层出现下沉位移，形成一定范围的免压拱，随着回采的进行，相邻矿柱上部所形成的免压拱会发生链接，形成一个位于所有采空区矿柱顶部的大免压拱，即在采空区的上部会产生一个半径为Rp的免压拱塑性区。 塑性区的范围不仅受到岩体性质、开采断面的影响，还与采空区的埋深有关。 矿体开挖后，采空区的顶板围岩中会产生一个普氏拱，只要矿柱能承受顶板围岩免压拱塑性区范围内岩体的自重应力，就能保证长期稳定。

图1 基于普氏理论的矿柱承载机理分布

根据普氏拱理论和矿柱承压机理可知，矿柱所承受的荷载为其顶板上方塑性区范围内所有岩体的重力之和，可计算出免压拱中塑性区的半径Rp为：

式中R0为开挖半径，m；P0为开挖处的垂直自重应力，MPa；c为岩体内聚力，MPa；φ为岩体内摩擦角，（°）；γ为上覆岩层岩石容重，kN/m3；H为开采深度，m。

在任何一种情况下，矿柱宽高比都会对矿柱强度产生“尺寸”效应。 单个分层中的矿柱可采用平均应力进行受力平衡分析［9］。 在分层中设计矿柱尺寸时应该考虑矿柱中的峰值压应力集中。 事实上，在单层矿柱设计方法中，基于平均压力的设计方法而非峰值应力应用最为广泛。 矿柱设计的面积承载方法是基于简单的力学平衡分析，如图2 ～3 所示，当采场力学平衡时，要求底板对矿柱向上的力Fp等于上覆岩层荷载W，即：

式中σv为平均上覆岩层应力，MPa；A为矿柱所承载岩柱的横截面积，m2；σp为矿柱内平均应力，MPa；Ap为矿柱横截面积，m2。

而矿柱所承载区域的面积A ＝Ap+Am，其中Am是矿柱所支撑采空区的面积，则矿柱所受的应力σp为：

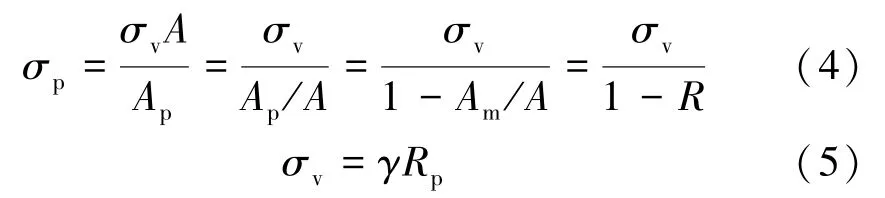
式中R ＝Am/A，定义为面积提取率；Ap＝Wp× Lp；A＝（Wo+Wp） ×（Lp+Wc），Am＝Wo×（Lp+Wc）+Wc×Wp；Wo为矿房宽度；Wp矿柱宽度；σv为矿柱上覆塑性区引起的自重应力。

图2 矿房和矿柱组成的开挖示意图

图3 单个矿柱受力示意图

因此，矿柱内的应力σp为：

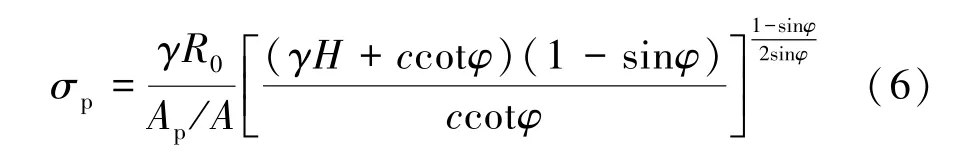
1.1.2 有效区域理论

杜瓦尔首先提出有效区域理论，而后被不断发展与完善，但其主要用于条带式开采的矿柱设计中［10］。有效区域理论假定各矿柱支撑上部及与其相邻的矿柱所平分的采空区上覆岩层的质量。 该方法计算方便、简单易行，在条形矿柱安全设计方面得到了广泛应用。

1.1.3 两区约束理论

两区约束理论由威尔逊提出并沿用至今，它根据不同的应力状态，将矿柱受力分为核区和屈服区两部分，两端屈服点向里为应力核区（矿柱变形较小），屈服点向外为屈服区（矿柱主要变形区域），并基于实验数据，确定了屈服区宽度和矿柱承载能力的计算公式［5，11］。 该理论综合考虑了矿柱的三轴强度特性，更加贴合于工程实际，应用广泛，但在岩体力学参数取值方面未加以阐述，实际应用过程中仍受到不少限制。

1.1.4 面积承载理论

目前国内设计院应用最为广泛的是矿柱面积承载理论，即空区内各矿柱所受到的荷载为采空区到地表岩层的自重应力，并假设矿柱支撑面积等于矿柱所分摊的顶板面积与其自身面积的总和［12-13］。 该理论在矿柱荷载计算方面简单易行，被广泛应用于工程实践，其矿柱内平均应力为：

上覆岩柱分摊的开采面积与矿柱布置形式紧密相关，矿山可根据研究内容的需要以及实际情况，选取最为恰当的平均应力计算公式。 在初期对研究区内采空区的矿柱稳定性分析中，可采用正方形矿柱平均应力计算公式来简化计算，此时矿柱平均应力为：

1.2 矿柱强度

100 多年以来，各国学者主要通过室内实验、现场原位实验2 种方式对矿柱强度展开研究。 根据实验结果和现场实际调查，并结合相关理论，得到了多种关于矿柱强度计算的公式。

Bieniawski 对煤柱强度尺寸效应进行了大量实测，认为煤柱强度不是简单地表现为尺寸越大强度越小，而是存在着一个临界煤柱尺寸，当矿柱实际尺寸大于临界尺寸时，煤柱强度将不再随尺寸增加而减小。 该理论认为煤柱强度与试样的尺寸之间存在如下关系：

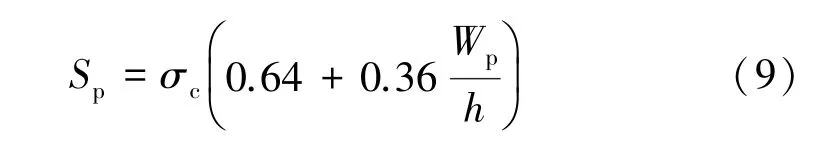
式中Sp为矿柱强度；σc为试样单轴抗压强度，MPa；h为矿柱高度，m。

1981 年，Bieniawski 对之前所提出的矿柱强度计算公式进行了修正，修正后的公式为：

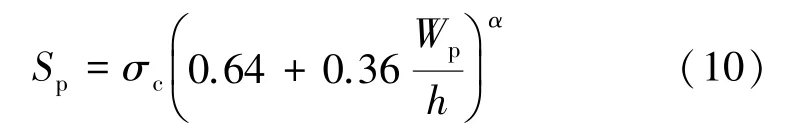
式中α 为常数，主要取决于矿柱宽高比，当其宽高比大于5 时，α 取1.4；否则α 取1.0。

1.3 矿柱安全系数

1.3.1 基于面积承载理论

矿柱安全系数是矿柱强度与矿柱平均应力的比值，根据前文所选取的矿柱强度与平均应力的计算公式，可以得到基于面积承载理论的矿柱安全系数K为：

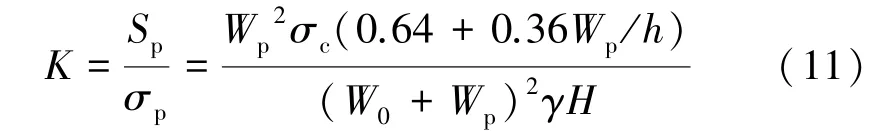
1.3.2 基于普氏理论

基于普氏理论和面积承载理论得到的矿柱应力σp（式（6））和Bieniawski 矿柱强度公式得到的矿柱强度Sp（式（10）），进行理论推导得到矿柱的安全系数为：

对于正方形矿柱，矿柱的安全系数为：

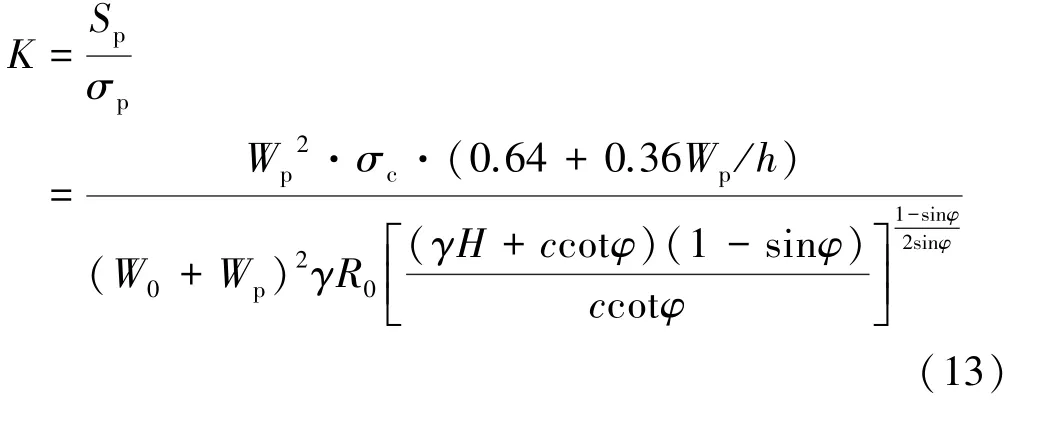
2 工程实例

湖南省某铅锌矿经历了约40 年的以空场法为主的地下开采，形成了数量巨大、范围广泛、空区层叠的采空区群。 体量巨大的采空区群时刻威胁着工作人员的生命和财产安全。 据统计，2009～2015 年间，铅锌矿区曾发生多起冒顶片帮、透水事故，造成数十名人员伤亡和大量财产损失。

本文以湖南省某铅锌矿区群采空区为研究对象，圈定了井下1 365 根矿柱样本。 对这些矿柱的安全系数进行逐一计算，最终得到了基于面积承载理论及普氏理论的各矿柱安全系数，如表1 所示。 篇幅有限，表2 为铅锌矿区Ⅴ矿区第3 采区矿柱安全系数计算结果。

表1 基于面积承载理论及普氏理论的矿柱安全系数分布情况

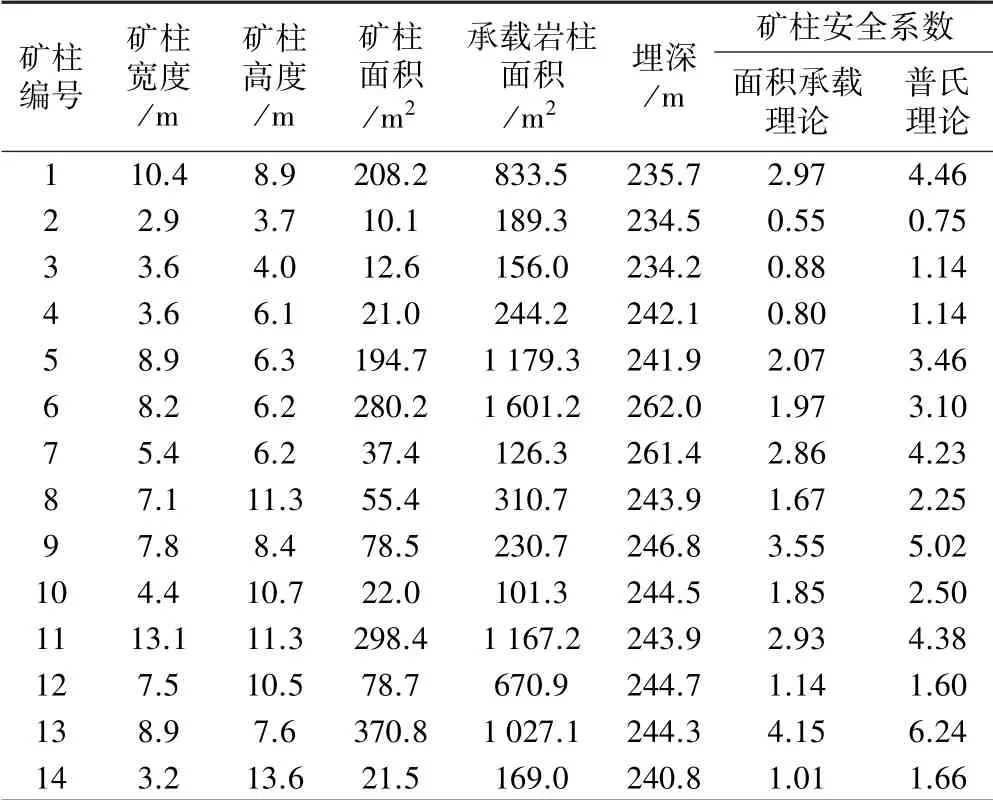
表2 铅锌矿区Ⅴ矿区第3 采区矿柱稳定性计算结果

通过以上分析可知，基于面积承载理论的矿柱安全系数有33.83%小于1，处于不稳定状态。 但据现场实际观察，这些矿柱仍保持良好的稳定形态，在一定时期内仍能起到对空区的支撑作用，这反证了基于面积承载理论的矿柱安全系数计算方法在该矿区的应用效果不佳，结果过于保守。 同时，与基于普氏理论的矿柱安全系数计算结果也有较大差异。

对比分析，得知该矿区两种矿柱安全系数计算方法之间的关系可分为3 类：①矿柱埋深50～100 m，两者数据基本相差不大，该类矿柱约占总数的10%。 ②矿柱埋深100～300 m，两者结果呈线性相关，该类矿柱约占总数的85%，两者线性关系为：K普＝1.472 2K面-0.023 1。③矿柱埋深300 m 以上，该类矿柱约占总数的5%，两者线性关系为：K普＝1.536 9K面-0.006 2。

3 矿柱安全系数三维数值模拟计算与分析

为寻找适合该铅锌矿区矿柱安全系数的计算公式，对该矿区1 365 根矿柱安全系数进行计算分析。通过正交试验可知，影响该铅锌矿区矿柱安全系数的关键因素主要为矿柱埋藏深度、矿柱横截面积、矿柱承载岩柱横截面积、矿柱高度。 为研究采场间距和埋深对矿柱稳定性的影响，通过Midas GTS 和FLAC3D耦合建模的方法，建立了矿柱间距分别为8 m、12 m、16 m、20 m，埋深100～1 000 m，矿柱尺寸均为6 m × 6 m × 8 m。以20 m 间距标准空区模型为例，空区高度8 m，矿柱间距20 m，空区内有9 根矿柱。 根据圣维南原理，所建立的模型尺寸为X ×Y ＝90 m × 490 m，Z方向以空区为界线分为两部分，上部分高度为埋深高度，下部分高度为200 m，模型的上部直达地表。 将在Midas 中建立好的三维网格模型，利用转换接口程序转换到FLAC3D软件中。 20 m 间距标准空区模型网格如图4所示。 由于篇幅有限，这里只列出20 m 间距部分标准空区模型及其计算结果，如图5 所示。

图4 20 m 间距标准空区模型

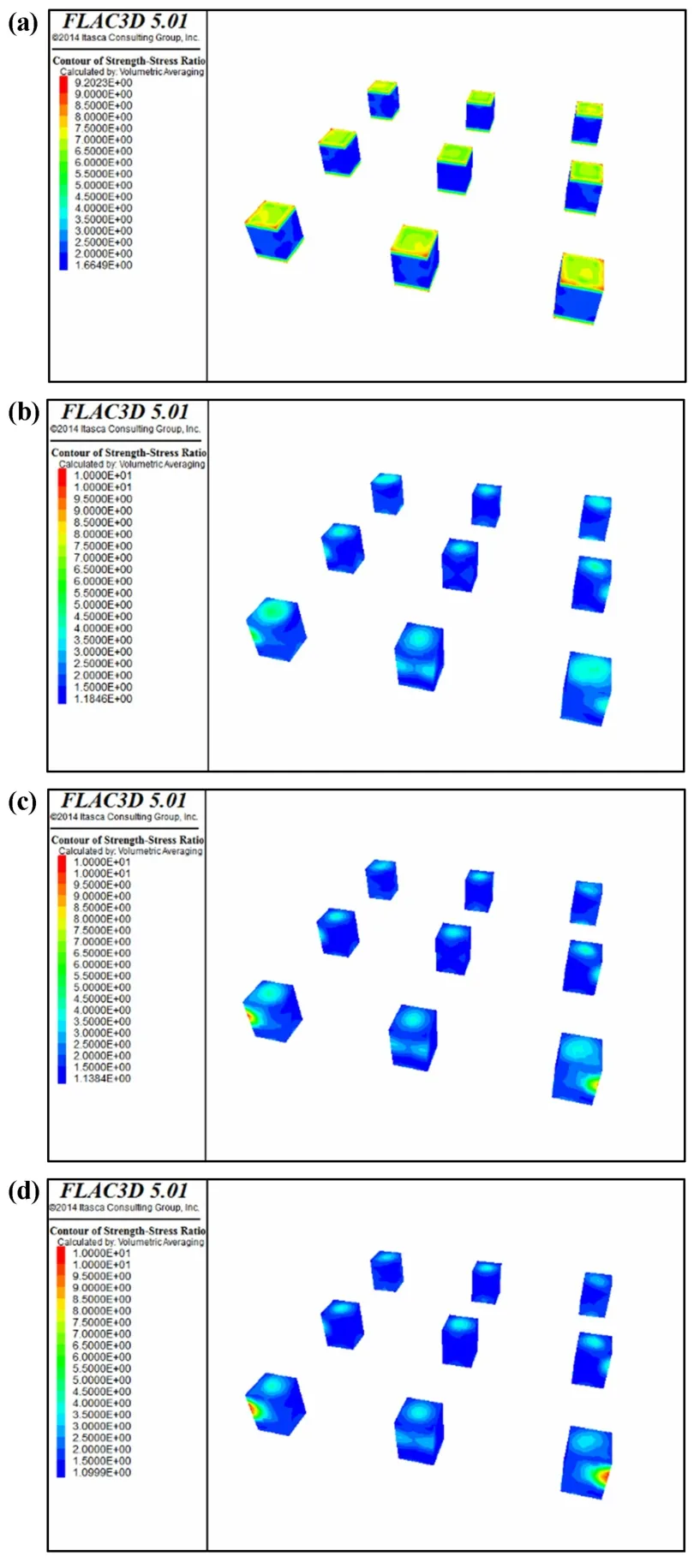
图5 不同埋深矿柱安全系数云图

在矿柱稳定的情况下，为了准确分析矿柱应力与矿柱埋深、矿柱间距之间的关系，统计不同间距、不同埋深情况下所有矿柱的安全系数，如表3 所示。

表3 20 m 间距下矿柱安全系数

可以看出在100 m、200 m 和300 m 埋深时，最小安全系数往往出现在矿柱的外表面位置，同时最小安全系数随着埋深增加而逐渐减小且都大于1，表明矿柱稳定性良好。 随着埋深增加，最小安全系数出现在矿柱的四周和顶部位置，表明随着上覆岩层重力增加，矿柱顶部所受压力增加，其安全系数也会相应减小。

4 矿柱安全系数优化研究

为了深入分析矿柱应力与矿柱埋深、矿柱间距之间的关系，通过Matlab 软件对所有的矿柱安全系数进行二元多项式拟合（如图6 所示），可得到矿柱应力与矿柱埋深、矿柱间距之间的函数关系式。 本文在进行矿柱稳定性分析时，均选用Bieniawski 矿柱强度公式，因此基于拟合出的函数关系，可推导出矿柱应力计算公式为：

式中σp为矿柱应力，MPa；L为矿柱间距，m；H为矿柱埋深，m。

图6 二元多项式拟合曲面图

基于Bieniawski 矿柱强度公式，可得出适合该矿区的矿柱安全系数计算公式为：

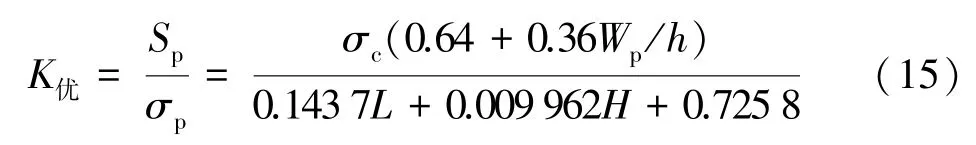
5 结 语

1） 基于面积承载理论对矿柱所受荷载进行了详细分析，推导出基于面积承载理论的矿柱安全系数的计算公式。 基于普氏理论推导了矿柱实际承载上覆岩层的厚度，通过力学平衡分析推导了单个矿柱内荷载的计算公式，最终推导出基于普氏理论的矿柱安全系数的计算公式。

2） 基于面积承载理论和普氏理论计算了采空区内1 365 根矿柱的安全系数，结果表明基于面积承载理论的矿柱安全系数计算公式过于保守，与现场实际不符。 对比分析可知，对于铅锌矿区埋深100 ～300 m的矿柱（占比85%），2 种理论计算的矿柱安全系数之间存在着线性相关性。

3） 通过Midas GTS 和FLAC3D耦合建模的方法，以铅锌矿区Ⅴ矿区3 采区为例，构建了不同矿柱间距与矿柱埋深的标准空区模型，研究矿柱应力与矿柱间距、矿柱埋深之间的关系，并通过Matlab 软件进行二元多项式拟合，最终得到了优化后的矿柱安全系数计算公式。

4） 本文仅对矿柱上覆荷载进行了优化研究，未对矿柱强度公式作进一步讨论，有待下一步细化研究。