某铁矿无底柱分段崩落法的参数优化研究

简永军，陈玉明

(昆明理工大学 国土资源工程学院，云南 昆明 650093)



某铁矿无底柱分段崩落法的参数优化研究

简永军，陈玉明

(昆明理工大学 国土资源工程学院，云南 昆明 650093)

结合云南某铁矿的生产地质条件和矿石的赋存条件，运用PFC3D数值模拟软件建立矿山采场的放矿模型，对该矿山采场结构参数，即崩矿步距，进路间距尺寸和分段高度进行优选。利用回贫差值大小衡量结构参数组合的优劣情况，即回贫差值越大，放矿效果越好，采场结构参数越优，反之，则差。通过正交试验设计建立9组不同的采场参数组合，并分别对9组试验验建立对应的PFC数值放矿模型，对最后的实验结果进行分析，经统计研究，最终确定该矿山的最优采场结构参数组合为分段高度为30 m，进路间距25 m，崩矿步距6 m。

结构参数；放矿指标；回贫差；PFC3D；正交试验；放矿模型

无底柱分段崩落法因其开采强度大，效率高，成本低，回采安全等优点，自20世界60年代引进国内并广泛引用于我国金属矿山。目前应用该法开采的矿石量约占地下矿山采出矿石总量的80%。崩落法回收矿石的基本原理就是在废石的覆盖下面，借助重力的作用在回采巷道中进行放矿。无底柱分段崩落法的采场结构参数包括崩矿步距，进路间距和分段高度，分段高度一旦设计开始凿岩切割，最不容易进行调整，近路间距次之，崩矿步距可根据矿山生产需要进行自由调整，他们的不同组合将直接影响到矿山的回收效益。本次研究矿山为国内最大的地下金属矿山之一，其主要地质储量均埋藏在深部，适宜采用大型采掘设进行井下开采，地下开采规模可达400万t/a。进路间距，分段高度和崩矿步距的最佳关系组合协调，是获取良好放矿效果和经济效益的关键。椭球体的排列步分布形式，将会直接影响到矿石的损失，在设置结构参数时，应尽量使放出椭球体两两相切，即左右椭球体分别和上下两椭球体相切，经大量文献资料研究表明，两两相切时放矿效果最好，经济效益最高。放出椭球体在垂直于回采进路的剖面上有两种排列形式，如图1所示。

1) 椭球体采用高分段布置时，分段高度与进路间距的关系如下：

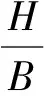
(1)

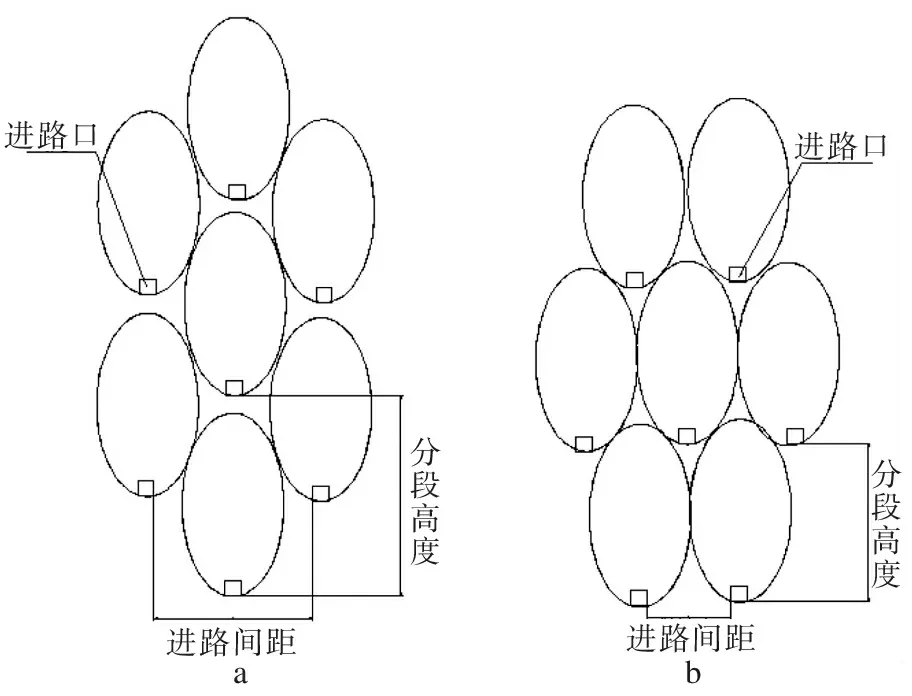
a 大间距放出椭球体布置形式；b 高分段放出椭球体布置形式

2) 椭球体采用大间距布置时，分段高度与进路间距的关系如下：

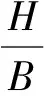
(2)

式中H——分段高度；

B——进路间距；

a——放出椭球体的长轴；

b——放出椭球体的短轴。

1 PFC3D数值模拟的基本原理和方法

PFC(Particle Flow Code)颗粒流分析程序是以圆盘(PFC2D)或球(PFC3D)作为基本单元来模拟球形介质的运动和相互碰撞情况，允许介质发生旋转和位移，计算过程中，也可以允许介质发生分离并重新构建新的接触。其利用显示差分算法和离散理论对微细观颗粒的力学进行分析统计，并从粒子的基本结构来考虑介质的基本力学特性和运动行为。颗粒离散元法中颗粒的位置(position)和速度(velocity)由牛顿运动定律和力与位移方程间的关系计算，不断使用迭代计算法来更新各个颗粒速度、位置、受力状态和接触状态[1-3]，其计算循环过程如图2所示。

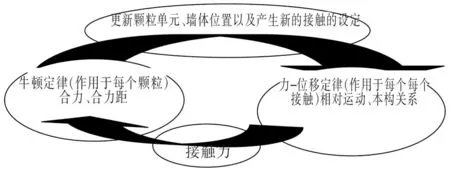
图2 颗粒位置和速度的计算循环过程

离散元法是在1979年由cundall和strack提出的，其基本观点为把不连续介质分离成刚性元素的集合体，使每个刚性颗粒或单元都满足运动方程,并用迭代算法来求解每个刚性元素的运动轨迹方程，从而可以求解不连续体的整体运动情况。离散单元法是把介质看成是有一系列的单元粒子组成，根据离散单元本身所具有的特性建立起数学模型，将需要分析和研究的物体看作是离散颗粒的集合，这与离散单元的离散性质基本相一致，所以，应用离散单元法来分析颗粒的运动情况和过程非常有效和突出。

PFC3D数值模拟过程中作了如下的基本假设：

1) 颗粒为圆形盘(二维)或球体(三维)；

2) 颗粒单元为刚性体；

3) 接触为点接触；

4) 接触特性为柔性接触，颗粒之间的重叠量远远小于球体的半径；

5) 在接触处有粘结强度。

2 PFC3D模型的建立

2.1方案设计

本文研究的铁矿山采用无底柱分段崩落法开采矿石，一期设计生产能力为400万t/a，矿块生产能力为60万t/a，该矿山是我国最大的地下金属矿山之一，目前采用的采场结构参数为20×20，即分段高度和进路间距皆为20 m，在国内属于高分段大间距参数，一直处于领先水平。二期采用高变分段的放矿形式，分段高度20，30 m不等，为了减少矿石的损失贫化，提高矿山的生产效益和回收能力，需确定采场结构参数的优选组合。本次模拟试验采用三因素三因子水平L9(34)进行正交试验，三因素：分段高度、进路间距和崩矿步距，根据各因子的正交设计组合，建立9组正交试验方案见表1。

表1 正交试验方案 m

2.2模型建立

鉴于PFC3D数值模拟对所模拟空间尺寸结构大小无限制，则本次模拟试验所建模型与现场尺寸比例为1∶1。本次试验采用端部放矿，在模型的底部预留3～4个出矿口(相当于矿块采场进路)。模型尺寸为130 m×80 m×(5～7) m(长×高×宽)，出矿口尺寸为4 m×4 m(高×宽)，现根据矿山实际情况和设备能力的大小，利用PFC3D命令程序建立9组中一组结构参数放矿模型：分段高度30 m，进路间距25 m，进路尺寸为4 m×4 m(宽×高)。本次试验拟采用2个分段，3～4个进路，边孔角为60(°)，设计图见图3a，颜色较浅为废石，颜色较深为矿石。利用PFC3D里面的wall建立模型见图3b。

a 放矿试验设计；b 放矿模型

2.3颗粒参数的选择

根据矿山生产实际情况和矿体的赋存条件，并查阅相关文献参考以前研究的相似结果[4]，得到本次模拟的颗粒参数值，本次试验模型中包括矿石和废石两种球体，矿石颗粒半径取0.5 m，废石颗粒取0.8 m，刚开始首采分层的矿岩界面为水平状态，模拟所需要的参数为：颗粒半径，颗粒和墙法向刚度和切向刚度，颗粒密度，局部阻尼系数，颗粒间和颗粒墙间的摩擦系数，颗粒颜色通过对颗粒分组改变其颜色，本次模拟设定废石为红色(group1)，矿石为黄色(group2)，颗粒参数值如表2所示。

表2 颗粒主要参数

2.4 PFC3D放矿模拟

本次模拟的放矿条件采用20%的截止品位控制放矿，放矿初期矿岩接触面呈水平状态，放出矿石为纯矿石，计算一定时间后，矿岩接触面缓慢下降，当下降一定高度后，接触面开始出现凹凸不平现象，随着放矿的不断进行，凹凸不平现象会更加明显，当矿岩接触面到达放矿口时，在进路之间形成脊部残留，残留高度为岩石开始混入的高度，若继续放矿，废石开始混入出现贫化，放矿到截止品位时停止放矿，放矿截止品位的计算公式如下[5]：

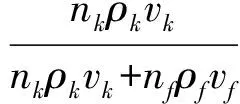
式中aj——放矿截止品位；

nk——矿石数量；

ρk——矿石密度；

vk——矿石体积；

nf——废石数量；

vf——废石体积；

ρf——废石密度；

ad——矿石地质品位。

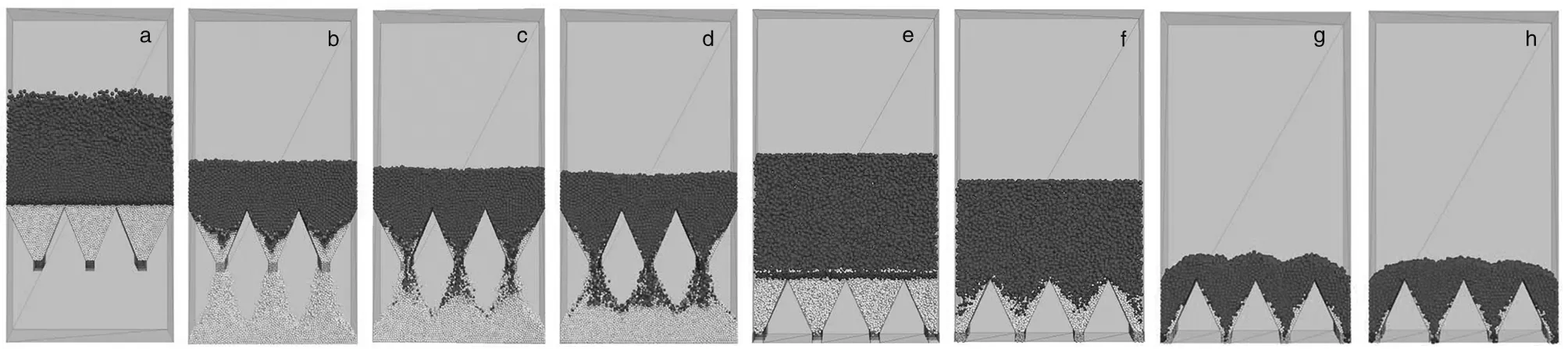
a 第1分段装矿及标志颗粒布置；b 第1分段循环7000步；c 第1分段标志颗粒回收过程；d 第1分段截止放矿；e 第2分段装矿及标志颗粒布置；f 第2分段放矿循环7000步；g 第2分段标志颗粒回收；h 第2分段停止放矿

2.5 PFC3D数值模拟结果分析

在矿山实际生产情况中，影响放矿的因素较多，除了采场结构参数组合外，还有如放矿方式，控制管理等影响因素，但是在数值模拟过程中，由于软件本身的缺点，考虑所有的影响因素也不现实，经大量研究结果表明[6-8]，本次试验只考虑3个主要的影响因子分段高度，近路间距和崩矿步距的影响。根据对9组数值试验各放出的矿石和废石颗粒数量的统计，计算出各组试验的回收率和贫化率，然后进行比较分析，见表3～4。

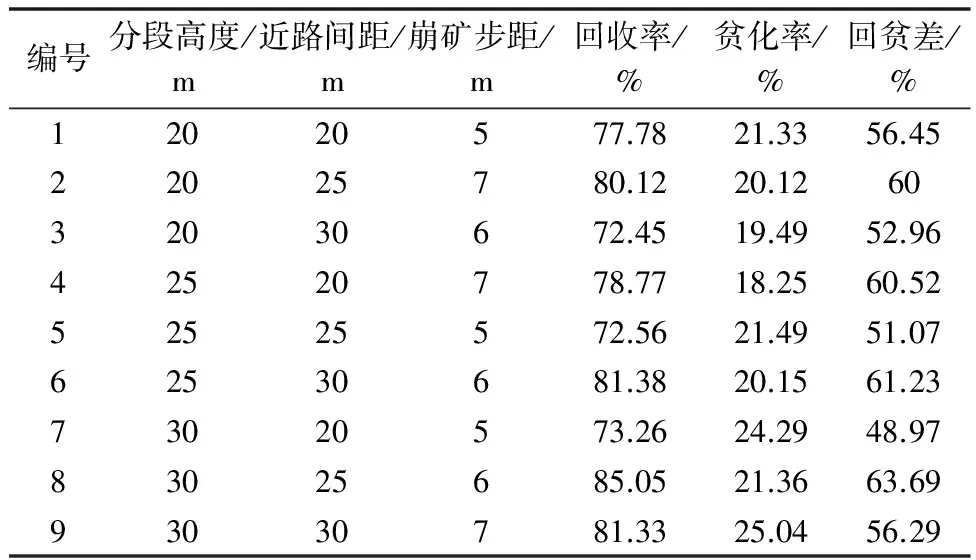
表3 第1分段结果分析

表4 第2分段结果分析

通过对9组试验得出的回收率和贫化率以及回贫差，可以直接看出每组结构参数组合的放矿效果。9组试验中回收率变化范围在85%～95%之间，与国内采用无底柱分段崩落法的金属矿山相比普遍高约5%～10%，即回收率偏大。而贫化率变化范围在18%～25%，普遍偏小，究其主要原因一：在矿山实际生产过程中，矿石中总是含有夹石，而在模拟过程中没有考虑进去，则使回收率偏高；原因二：在实际放矿过程中，大块废石中总含有细小废石，使得细小废石提前放出，而在数值模拟过程中，废石半径设置均匀，则贫化率偏低。

在9组试验中，每个模型的初始条件，边界条件以及球体的物理力学参数和放矿步骤相同，则认为此次模拟结果具有可比性。结合第1分段回收率，贫化率及回贫差的明显看出：编号1、2、3、4方案回贫差较低，在50%～60%之间；编号5、6、7、8、9方案中，编号8方案回收率较高，贫化率也较低，即回贫差大(回贫差越大，采场结构参数越优，放矿效果越好，反之，放矿效果越差)。本次矿山二期工程选择的主力采掘设备为Simba H1354 采矿台车钻凿深孔，凿岩深度可达40 m左右，所以设备性能可以满足采用高分段的要求。根据以上分析，推荐矿山采用30 m×25 m×6 m，回采进路尺寸为4 m×4 m的采场结构参数。

3 结 论

1) 采场结构参数的合理与否，将直接影响到矿石的损失贫化指标，乃至影响到整个矿山的经济效益，因此需要对采场结构参数进行优选组合研究，确定矿山合理的分段高度，近路间距，进路尺寸和崩矿步距等；

2) 利用PFC3D高效灵活的特点，克服PFC2D不能对崩矿步距优化的这一缺点，建立了研究矿山的数值放矿模型，对矿石和废石进行分组染色模拟矿岩流动的全过程，通过对9组试验的回贫差进行比较，得出该矿山分段高度30 m，近路间距25，进路尺寸为4 m×4 m，崩矿步距为6 m；

3) 在数值模拟过程中，回采矿石贫化率偏低，究其原因为矿体中夹有废石，而在模拟过程中，废石和矿石球体颗粒皆采用平均半径生成，没有考虑夹石对放矿的影响，故贫化率偏低。而回收率基本符合国内一般回收指标。

[1] Itasca. PFC3D-particle flow code in three dimensions, theory and background[M]. Minneapolis, Minnesota: Itasca Consulting Group, Inc, 2003.

[2] Bhandari A, Han J. Investigation of geotextile-soil interaction under a cyclic vertical load using the discrete element method[J]. Geotextiles and Geomembranes, 2010, 28(1): 33-43.

[3] Yang G, Wang X H. Discrete element modeling for granular mateials[J]. Electronic Journal of Geotechnical Engineering, 2012(17): 2463-2474.

[4] 刘志娜. 基于PFC数值模拟的无底柱采场结构参数优化研究[J]. 矿业研究与开发, 2008, 28(1): 3-5.

[5] 冯浩楠, 舒太镜, 郭建来. 某矿山无底柱分段崩落法最优参数研究[J]. 有色金属, 2015(7): 1671-4172.

[6] 吴爱祥, 武力聪, 刘晓辉, 等. 无底柱分段崩落法结构参数研究[J]. 中南大学学报, 2012, 43(5): 1846-1850.

[7] 董鑫, 邓红卫. 夏甸金矿无底柱分段崩落法采场参数优化[J]. 采矿技术, 2009, 9(3): 4-6.

[8] 黄兴益. 尖山铁矿无底柱分段崩落法结构参数研究[J]. 金属矿山, 2012(4): 5-7.

AStudyonParametricOpitimizationofPillarlessSublevelCavingforaIronOre

JIAN Yongjun, CHEN Yuming

(FacultyofLandResourceEngineering,KunmingUniversityofScienceandTechnology,Kunming,Yunnan650093,China)

Based on the geological conditions of production and the conditions of occurrence of an iron ore in Yunnan Province, the ore drawing model of mine stope was established by using PFC3D numerical simulation software. The structural parameters of the mine stope, that is, the interval of collapse and segment height. Using the difference between the poor and the poor, we know the structural parameters of the combination of the advantages and disadvantages of poor conditions is: the greater the difference back to the poor is, the better the effect of ore is, and stope structure parameters is better. Otherwise, it is poor. Nine sets of different stope parameter combinations were established by orthogonal experiment design, and the corresponding PFC numerical model was established respectively. The final experimental results were analyzed and statistically studied to determine the optimum of the mine. The combination of stope structure parameters is segment height of 30 m, with the approaching space of 25 m and collapse interval of 6 m.

Structural parameters; Ore-drawing index; Back-poor difference; PFC3D; Orthogonal test; Ore drawing model

2016-07-29

简永军(1990-)，男，贵州毕节人，在读硕士研究生，研究方向：采矿理论，手机：18487137647，E-mail:1055629762@qq.com.

TD853.36+2

：Adoi：10.14101/j.cnki.issn.1002-4336.2016.04.018