复杂荷载作用下残采矿柱综合安全系数
姜立春 ,王玉丹
(1. 华南理工大学 土木与交通学院,广东 广州,510640;2. 华南理工大学 安全科学与工程研究所,广东 广州,510640)
为了充分利用矿产资源,矿山需要对开采后遗留的大量预留顶、底板和矿柱等残矿体进行回收。残矿体赋存力学环境复杂,开采难度大。预留矿柱不仅受覆岩荷载的作用,同时还受爆破振动和崩落体矿岩侧向挤压等多种荷载作用。当外部作用荷载超过极限承载强度时,矿柱容易发生破损、断裂破坏,进而诱发采场坍塌[1−2]。另外,矿柱的稳定性与采场的深度、矿房宽度、岩性等因素密切相关。因此,准确评估矿柱的安全性是残矿回采需解决的首要问题。通过构建矿柱力学模型求取矿柱安全系数是评价矿柱稳定性的重要途径。国内外学者在此领域开展了相关研究[3−9]。王在泉等[7]以矿柱破裂面上节点的塑性应变或位移突变作为矿柱整体失稳的标志,采用有限元强度折减法计算了矿柱的抗剪安全系数。尹升华等[8]在分析矿柱荷载、强度、失稳势函数、破坏形式的基础上,总结了影响矩形矿柱稳定的8种主要因素,并根据影响因素建立了计算矩形矿柱安全系数的简化式。李江腾等[9]针对具有初始几何缺陷的超高矿柱稳定性问题,建立了矿柱力学简化模型,分析了弹塑性失稳的极限载荷。目前,国内外学者在分析矿柱安全系数时,通常仅考虑覆岩单一荷载作用,提出安全系数主要为剪切安全系数或压缩安全系数。由于忽略了爆破振动、崩落矿体侧向挤压等对矿柱的协同作用,计算结果存在一定偏差。因此,该类安全系数无法满足残矿开采安全评价的要求。本文作者在现场充分调研的基础上,综合考虑覆岩、爆破振动和崩落矿岩等对矿柱的协同作用,通过构建力学模型,研究残矿开采条件下矿柱安全系数的计算方法,评价矿柱安全性;利用工程实例验证该方法分析结果的可靠性,为残矿矿柱安全回采提供理论支撑。
1 矿柱力学分析
矿柱是采空区结构稳定的重要支撑单元,主要受上部覆岩自重作用。当回釆矿柱周边矿体时,爆破应力波会对矿柱产生侧向动荷载作用;采场内矿石没有及时运出,崩落矿岩将对矿柱产生侧向挤压作用(见图1)。
1.1 覆岩作用
覆岩载荷(σ0)在顶柱上的分布可视为线性均匀分布[10−11],与覆岩厚度、矿房宽度、矿柱宽度有关,计算式为

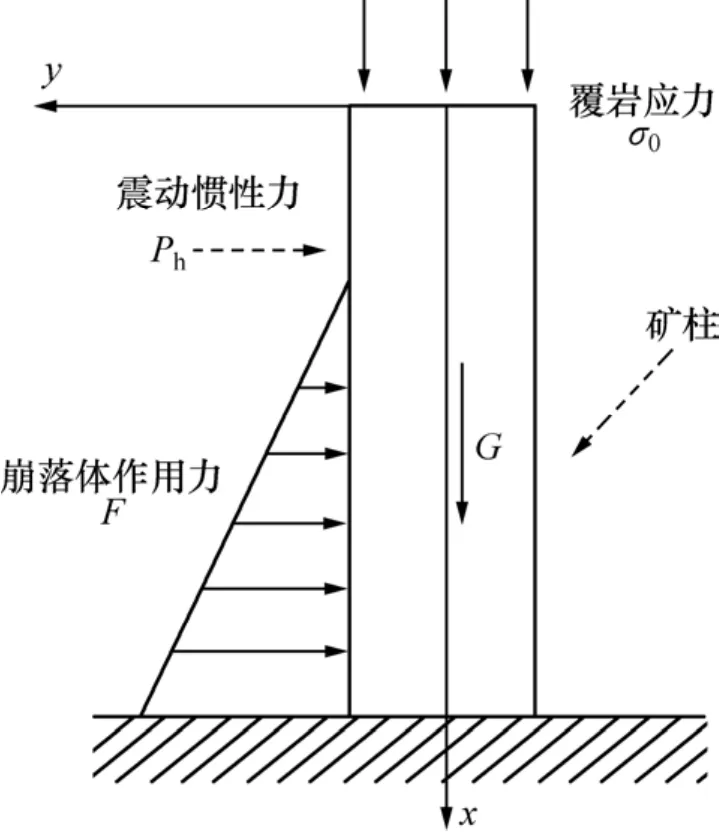
图1 矿柱力学分析Fig. 1 Pillar mechanics analysis
式中:γ0为矿体容重;z为覆岩厚度;a为矿房宽度;b为矿柱宽度。
1.2 爆破振动作用
这里采用惯性力法计算爆破振动荷载对矿柱的作用[12−13],可将爆破震动作用力分解水平方向的振动惯性力(Ph=ηG)和竖向的振动惯性力(Pv=η′G)(图 1)。

式中:G为岩体重力,bhγG0=;h为矿柱高度;Kh和Kv分别为岩体水平方向和竖直方向地震系数,根据文献[14],二者的取值分别 0.2和 0.07;Cz为综合影响系数,取 0.25,ai为矿柱上部的爆破振动加速度分布系数,由文献[15]可知,ai取1.8。
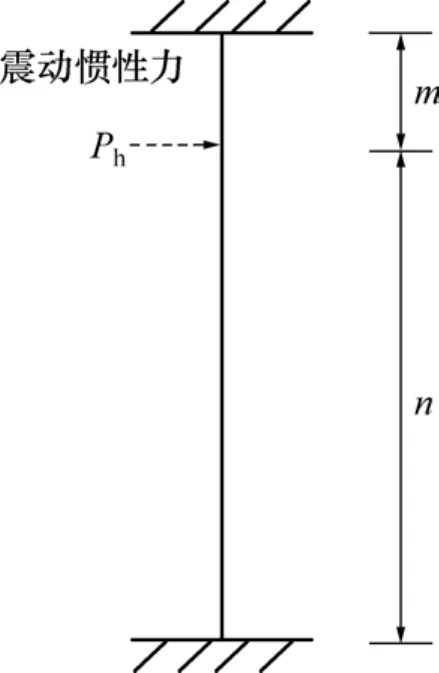
图2 柱力学简化模型Fig. 2 Mechanics simplified model
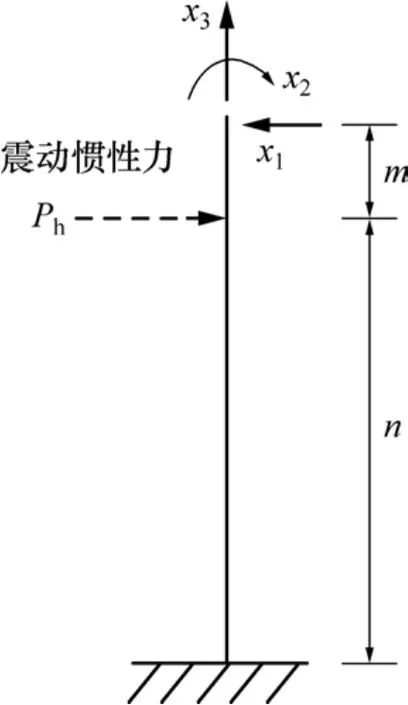
图3 基本体系Fig. 3 Basic system
假设矿柱高为h,爆破振动荷载作用于矿柱上端,与矿柱上部距离为m。此时,可将矿柱简化为两端固定的超静定结构体(图2),将水平惯性力视为集中应力施加于矿柱上进行分析。此时,矿柱产生一定的弯矩,引起矿柱垂直方向的应力变化。
矿柱力学简化模型有3个多余约束,为3次超静定结构。去除矿柱上端支座约束后得到基本体系(图3)。根据矿柱下端处水平位移、竖向位移和转角均为0的条件,可得矿柱位移方程式:

求解可得矿柱任一截面的弯矩M为

在水平爆破振动作用下,矿柱作用力函数σx2为

由于竖向爆破振动在方向与矿柱轴向一致,水平方向上产生的作用力分布差异较小,因此,的计算式为

1.3 崩落体作用
崩落体对矿柱产生侧向挤压作用,侧向压应力(F)计算式为

式中:λ为崩落体侧压系数;γ为崩落体容重;H1为崩落体高度。
在崩落体的侧向挤压作用下,矿柱内部将产生侧向应变。由于垂直方向应变很小可忽略不计,因此,矿柱的应变问题可简化为平面应变进行处理。
矿柱承受的垂直应力(σx)主要由自重(G)及覆岩应力(σ0)构成,水平应力(σy)主要为崩落体侧向压应力(F)。因此,矿柱水平方向应力函数为
式中:φ为应力函数;f(y)为关于y的函数式。
根据弹性力学原理[16],对式(11)进行积分运算,可得应力函数φ的表达式。依据边界约束条件,崩落体作用下矿柱的应力分量为:

式中:σx1,σy和τxy分别为崩落体对矿柱产生的垂直方向应力、水平方向应力和剪切应力。
2 矿柱破坏形式
矿柱破坏形式主要包括脆性断裂破坏、延性破坏、弱面剪切破坏(图4)[8]。岩石破坏时不产生明显的变形为脆性破坏(图 4(a)和(b));破坏时产生明显的塑性变形而不呈现明显的破坏面为塑性破坏(图 4(c)和(d))。在覆岩、爆破振动及崩落体挤压等多种荷载共同作用下,矿柱受力主要为拉应力、压应力和剪切力,破坏形式主要为压缩破坏和剪切破坏;当垂直方向最大压应力超过矿柱允许极限抗压强度时,矿柱将发生脆性破坏;当最大剪切应力超过矿柱允许极限抗剪强度时,矿柱发生塑性破坏。
因此,在综合考虑压缩破坏和剪切破坏对矿柱影响的基础上,提出综合安全系数K,分析评价矿柱的安全性。

图4 矿柱破坏形式Fig. 4 Pillar failure modes
3 矿柱安全系数
3.1 压缩安全系数(K1)

矿柱强度与矿柱的宽高比及岩体单轴抗压强度有关,根据BIENIAWSKI等[17]提出的计算式,可得矿柱抗压强度(σp)计算式:

式中:σp为矿柱抗压强度;σr为岩体单轴抗压强度;β为常数,根据矿柱的宽高比而定[17],当宽高比大于 5时,β=1.4,当宽高比小于5时,β=1.0。
为了保证矿柱安全,矿柱强度极限条件须满足:σp≥P,矿柱压缩安全系数(K1)计算式为

当K1<1时,矿柱将发生压缩破坏;当K1=1时,矿柱将处于临界破坏状态;当K1>1时,矿柱将处于稳定状态。K1越大,矿柱越稳定。
3.2 剪切安全系数(K2)
矿柱剪切安全系数为剪切面的抗剪强度与最大剪应力的比值。根据Mohr-Coulomb强度准则,可得矿柱在滑动剪切面上的抗剪强度(τf)。
在覆岩、崩落体挤压、爆破振动等载荷的作用下,矿柱剪切面上的剪切应力(τmax)与崩落体和覆岩对矿柱的剪切应力(τxy)相等。为保证矿柱安全,矿柱抗剪强度应大于极限抗剪强度,即:τf>τmax,可得矿柱剪切安全系数(K2):

式中:τmax为剪切面上的剪切应力;τf为剪切面上的抗剪强度。
分别将参透系数设为0.01 m/d、0.05 m/d、0.10 m/d、0.50 m/d、1.00 m/d、2.00 m/d、3.00 m/d、5.00 m/d,研究不同渗透系数对双排水盲沟渗流的影响。其余参数按计算实例取。计算结果见表5和图8、图9。
当K2<1时,矿柱将发生剪切破坏;当K2=1时,矿柱将处于临界状态;当K2>1时,矿柱将处于稳定状态。K2越大,矿柱越稳定。
3.3 综合安全系数(K)
综合安全系数是矿柱极限应力与最大压应力的比值,是矿柱稳定性的定量评价指标。全面考虑矿柱破坏形式(图 4),综合安全系数(K)取值为压缩安全系数和剪切安全系数两者之间的较小值,计算式为
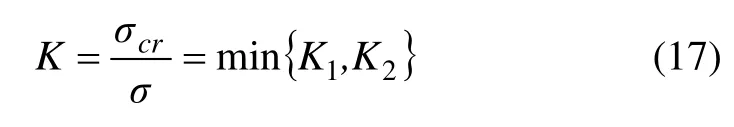
式中:K为综合安全系数;σcr为矿柱极限应力;σ为矿柱轴向最大压应力。
当K=K1时,矿柱主要为压缩破坏;当K=K2时,矿柱主要为剪切破坏;当K介于K1和K2之间时,矿柱将同时发生剪切、压缩破坏。
4 算例分析
某大型金矿山位于秦岭褶皱系南秦岭印支褶皱带凤县—镇安褶皱束的北缘,含金角砾岩带(AnKsb)主要分布于泥盆系中统古道岭组地层中,矿床赋存于该含金角砾岩带。地层主要由泥盆系中统的王家楞组(D2W)、古道岭组(D2g)的碎屑岩和碳酸岩组成。矿山由 KT8,KT5,KT9,KT7,KT2和KT6共6个矿体组成。
4.1 不同矿柱尺寸预留矿柱分析
根据该大型金矿山的现场实际情况,取20组不同宽度和高度组合的预留矿柱进行分析(其他条件不变)。矿柱高度分别为10,15,20,25和30 m,各自对应矿柱宽度分别为5,8,10和12 m,根据矿山实际情况及现场实验,矿柱安全系数计算时的物理参数见表2。

表1 矿柱物理参数Table 1 Pillar physical parameters
由式(17)和(20)可得不同规格矿柱的压缩安全系数(K1)、剪切安全系数(K2)、综合安全系数(K)变化曲线图。
图5所示为矿柱宽度一定、不同高度情况下,矿柱安全系数变化趋势图。由图 5可知:K1和K2均与矿柱高度负相关,K2的变化斜率大于K1的变化斜率。从图 5(a),(b)和(d)可以看出:K2>K1,K=K1。由图5(c)可知:当矿柱宽度为10 m,高度小于20 m时,K=K1,矿柱表现为压缩破坏;当高度大于20 m时,K=K2,结合图4(d)可以发现,矿柱表现为剪切破坏。
究其原因,在覆岩作用下,覆岩与矿柱端面间发生摩擦作用,由此在矿柱端面产生横向约束,矿柱近似处于三轴受压状态,矿柱破坏主要由压缩破坏引起。因此,矿柱高度越大,其抗压强度越低;矿柱高度越小,其抗压强度越高。当高度增大到某一临界值时,矿柱破坏形式发生突变,由压缩破坏转化为剪切破坏(图 5(c))。
图6所示为矿柱高度一定、不同宽度情况下,矿柱安全系数变化趋势图。从图6可知:当高度一定时,K2与矿柱宽度负相关;K1与矿柱宽度呈正相关,但变化幅值波动较小。当矿柱宽度小于10 m时,K=K1,结合图 4((a)和(b)),矿柱破坏形式主要为压缩破坏;当矿柱宽度大于10 m时,K=K2,结合图4(c),矿柱破坏形式主要为剪切破坏。
由式(14)可知,当高度一定时,矿柱抗压强度与宽度正相关,随着宽度增加而增大;当超过极限阀值,矿柱产生不可恢复的塑性变形,塑性区随着宽度增加不断扩展贯通;当宽度增加到某一数值时,矿柱剪切应力大于极限阀值,破坏形式由压缩破坏转化为剪切破坏。
4.2 不同崩落体高度矿柱分析
矿柱尺寸一定时,矿柱宽度b为10 m,高度h为30 m,崩落体高度H1分别为12,16,20,24和28 m,由式(15)和(16)分别计算压缩安全系数、剪切安全系数。图7所示为矿柱尺寸一定时,不同崩落体高度安全系数变化趋势图。由图7可知,K1与崩落体高度正相关,K2与崩落体高度负相关,K=K2。当崩落体高度为20 m时,综合安全系数为1.04,接近其稳定的临界值1.00。
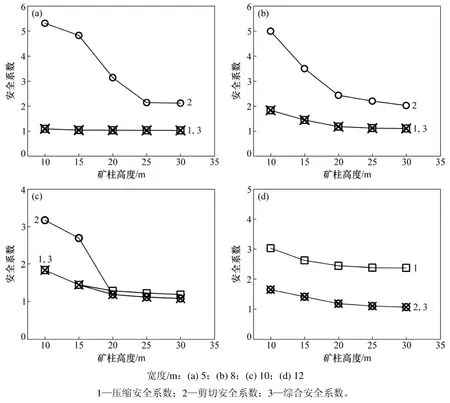
图5 不同高度的矿柱安全系数Fig. 5 Pillar safety factors of different heights

图6 不同宽度的矿柱安全系数Fig. 6 Pillar safety factor of different widths

图7 宽度10 m时,不同崩落体高度下的矿柱安全系数Fig. 7 Pillar caving safety factor when body height changes with width 10 m
究其原因,在崩落体侧向应力作用下,矿柱处于两轴受压状态,矿柱抗压强度大于其单轴受压强度;随着崩落体高度增加到某一值,矿柱综合安全系数减少到临界阀值1,矿柱将处于剪切失稳状态。
5 工程验证
该大型金矿山KT5矿体1 420 m已经进行了浅孔留矿法开采,55~57勘探线为采空区,57~59勘探线为釆准残矿体。为了保证釆准作业安全,需要在采场57线附近预留矿柱,设计图如图8所示。

图8 采场和矿柱纵剖面图Fig. 8 Longitudinal profile of stope and pillar
在残采过程中,采空区矿柱高度(h)为30 m,宽度(b)为10 m,爆破荷载施加在离顶板0.6 m位置。崩落体充填高度(H1)等于矿柱高度(h)。矿柱计算模型如图1所示,依据该矿山岩体实测数据,岩体力学参数选取如表2所示。
由矿柱安全系数计算式(15)和(16),可得矿柱的压缩安全系数为1.29,剪切安全系数为1.33,均超过安全临界值1.00。由前面分析,矿柱综合安全系数取压缩安全系数、剪切安全系数的较小者,即K=K1=1.29。此时,矿柱处于稳定状态。
现场40 d跟踪表明,随着回采由1个分层推至3分层,采场高度由10 m增加到30 m,未发生采场顶板坍塌、矿柱失稳现象。图9所示为回采结束后典型的采场矿柱实景图。现场位移监测也表明,采场和矿柱没有发生局部塌陷现象,采场和矿柱安全性良好,验证了理论计算结果的可靠性。

表2 岩体力学参数Table 2 Rock mechanics parameters

图9 采矿过程和结束现场Fig. 9 Mining scene in process and final process
6 结论
1)考虑覆岩荷载、崩落体荷载及爆破震动荷载协同作用对矿柱稳定性的影响,构建综合载荷作用下矿柱受力模型,给出采场内崩落体、爆破震动对矿柱作用的应力函数表达式。
2)通过矿柱压缩、剪切破坏形式的分析,提出了矿柱压缩安全系数(K1)、剪切安全系数(K2)和综合安全系数(K)计算式,研究覆岩、崩落体及爆破震动荷载对矿柱稳定性的影响。
3)当矿柱宽度一定时,矿柱3种安全系数随着高度的增加逐渐递减,递减趋势减缓;当矿柱高度一定时,矿柱压缩安全系数随着宽度的增加而增加,剪切安全系数随着宽度的增加而递减,递减趋势减缓。工程实例验证了矿柱安全系数计算的可靠性。
[1]胡建华, 阮德修, 周科平, 等. 基于空区结构效应的残矿开采作业环境安全辨识与协同利用[J]. 中南大学学报(自然科学版), 2013, 44(3): 1122−1130.HU Jianhua, RUAN Dexiu, ZHOU Keping, et al. Identification and synergic use of operating environment safety based on structure effect of goafs in residual mining[J]. Journal of Central South University (Science and Technology), 2013, 44(3):1122−1130.
[2]罗周全, 管佳林, 冯富康, 等. 盘区隔离矿柱采场结构参数数值优化[J]. 采矿与安全工程学报, 2012, 29(3): 261−264.LUO Zhouquan, GUAN Jialin, FENG Fukang, et al. Stope structural parameters of panel isolation pillar numerical optimization[J]. Journal of Mining & Safety Engineering, 2012,29(3): 261−264.
[3]IDRIS M A, SAIANG D, NORDLUND E. Stochastic assessment of pillar stability at Laisvall mine using Artificial Neural Network[J]. Tunneling and Underground Space Technology, 2015, 49: 307−319.
[4]WATTIMENA R K, KRAMADIBRATA S, SIDI I D, et al.Developing coal pillar stability chart using logistic regression[J].International Journal of Rock Mechanics and Mining Sciences,2013, 58: 55−60.
[5]李夕兵, 李地元, 郭雷, 等. 动力扰动下深部高应力矿柱力学响应研究[J]. 岩石力学与工程学报, 2007, 26(5): 922−928.LI Xibing, LI Diyuan, GUO Lei, et al. Study on mechanical response of highly-stressed pillars in deep mining under dynamic disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 922−928.
[6]张涛, 张帅, 张百胜. 矿柱安全留设尺寸的宽度折减法与应用[J]. 岩土力学, 2014, 35(7): 2041−2046.ZHANG Tao, ZHANG Shuai, ZHANG Baisheng. Width reduction method and its application to determining safety size of pillar[J]. Rock and Soil Mechanics, 2014, 35(7): 2041−2046.
[7]王在泉, 李华峰. 矿柱抗剪安全系数的数值计算方法及分析[J]. 采矿与安全工程学报, 2010, 27(2): 277−280.WANG Zaiquan, LI Huafeng. Numerical calculation method for shear safety[J]. Journal of Mining & Safety Engineering, 2010,27(2): 277−280.
[8]尹升华, 吴爱祥, 李希雯. 矿柱稳定性影响因素敏感性正交极差分析[J]. 煤炭学报, 2012, 32(增刊1): 48−52.YIN Shenghua, WU Aixiang, LI Xiwen. Orthogonal polar difference analysis for sensitivity of the factors influencing the ore pillar stability[J]. Journal of China Coal Society, 2012,32(S1): 48−52.
[9]李江腾, 曹平. 初始几何缺陷对超高矿柱稳定性的影响[J].岩石力学与工程学报, 2005, 24(22): 4185−4189.LI Jiangteng, CAO Ping. Effect of initial geometrical imperfections on stability of ultrahigh pillar[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4185−4189.
[10]姜福兴, 张兴民, 杨淑华, 等. 长壁采场覆岩空间结构探讨[J].岩石力学与工程学报, 2006, 25(5): 980−983.JIANG Fuxing, ZHANG Xingmin, YANG Shuhua, et al.Discussion on the long wall overlying strata spatial structure[J].Chinese Journal of Rock Mechanics and Engineering, 2006,25(5): 980−983.
[11]苏仲杰, 于广明, 杨伦. 覆岩离层变形力学机理数值模拟研究[J]. 岩石力学与工程学报, 2003, 22(8): 1287−1290.SU Zhongjie, YU Guangming, YANG Lun. Overburdens Numerical Simulation of Deformation Mechanism Mechanics[J].Chinese Journal of Rock Mechanics and Engineering, 2003,22(8): 1287−1290.
[12]王运永, 高永涛, 蔡嗣经, 等. 考虑地震影响的地下连续墙稳定性拟静力法研究[J]. 北京科技大学学报, 2010, 32(5):559−564.WANG Yunyong, GAO Yongtao, CAI Sijing, et al. Research on the stability of diaphragm walls subjected to earthquake using pseudo-static method[J]. Journal of University of Science and Technology Beijing, 2010, 32(5): 559−564.
[13]刘如山, 胡少卿, 石宏彬. 地下结构抗震计算中拟静力法的地震荷载施加方法研究[J]. 岩土工程学报, 2007, 29(2):237−242.LIU Rushan, HU Shaoqing, SHI Hongbin. Study on seismic loading of pseudo-static approach used in the seismic design of underground structure[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(2): 237−242.
[14]耿萍, 何悦, 何川, 等. 地震系数法隧道上覆土柱的合理计算高度[J]. 重庆大学学报, 2013, 36(4): 160−164.GENG Ping, HE Yue, HE Chuan, et al. Advisable calculation heights of tunnel overlaying soil with earthquake coefficient method[J]. Journal of Chongqing University, 2013, 36(4):160−164.
[15]刘红帅, 薄景山, 杨俊波. 确定岩质边坡地震安全系数的简化方法[J]. 岩土工程学报, 2012, 31(6): 1108−1114.LIU Hongshuai, BAO Jingshan, YANG Junbo. Simplified method to determine the seismic safety factor of rock slope[J].Chinese Journal of Rock Mechanics and Engineering, 2012,31(6): 1108−1114.
[16]GB 50111—2006, 铁路工程抗震设计规范[S].GB 50111—2006, Code for seismic design of railway engineering[S].
[17]BIENIAWSKI Z T, VAN HEERDEN W L. The significance of in situ tests on large rock specimens[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1975, 12(4): 101−113.

