基于视觉测量的环形轨底座位姿标定方法

张阿龙, 章　明, 乔明杰, 朱伟东, 梅　标

(1.浙江大学 机械工程学院,浙江 杭州 310027； 2.西安飞机工业(集团)有限责任公司,陕西 西安 710089)



基于视觉测量的环形轨底座位姿标定方法

张阿龙1, 章明1, 乔明杰2, 朱伟东1, 梅标1

(1.浙江大学 机械工程学院,浙江 杭州 310027； 2.西安飞机工业(集团)有限责任公司,陕西 西安 710089)

摘要:为了提高环形轨道制孔系统转站之后的定位精度,消除由制造、装配、安装以及运动误差对其造成的影响,提出基于视觉测量的环形轨道制孔系统底座位姿标定方法.针对环形轨道制孔系统进行几何建模并确立手眼关系,建立从底座坐标系到相机坐标系的坐标系系统,论述视觉测量原理.通过对预制基准孔进行测量,并结合基于Levenberg-Marquardt最小二乘算法的孔位匹配方法,确定实际底座坐标系与理论飞机坐标系之间的关系,完成环形轨道制孔系统的底座坐标系位姿标定.实验结果表明:基于视觉测量的底座坐标系位姿标定方法,误差小于2 mm,成本低廉、操作简单且完全满足底座坐标系位姿标定要求.

关键词：环形轨道制孔系统; 几何建模; 视觉测量; 最小二乘法; 底座坐标系标定; Levenberg-Marquardt

飞机装配是一项技术难度大、涉及多学科领域的综合性集成技术,在很大程度上决定了飞机的制造成本、生产周期和装配质量,是整个飞机制造过程中的核心技术[1].一架大型飞机具有约150～200万个结构组件[2],各零部件之间主要采用机械连接,因而连接孔的质量对飞机的疲劳寿命有着重要影响.为满足现代飞机高寿命、高可靠性的要求,近年来,机器人自动化制孔系统以其低成本、高效率和成孔质量高等优点被广泛地应用于大型飞机装配中[3-7].然而,由于机器人本身工作空间的局限性,机器人自动化制孔系统并不适用于某些大型区域的制孔.以机身桶段对接区域制孔为例,成千上万的待制连接孔分布在绕机身360°的环形区域内,这给机器人转站制孔带来很大困难,而采用多个机器人进行制孔又会使制造成本大幅上升.因此,传统的机身对接区域一般采用人工制孔的方式解决.但是,这种方式不仅效率低下,而且工人劳动强度大,成孔质量也难以保证.

为满足大型飞机装配中机身段对接区域高效、高精度、低成本的制孔需求,浙江大学自主研制出专用于大型飞机前中、中后机身段对接区域制孔的环形轨道制孔系统.该套系统采用环形、双层轨道结构,并在此基础上引入步进式自动转站法,解决了飞机装配对接区域全覆盖、全自动化制孔问题.然而,自动转站运动过程实际上属于站位粗定位,存在较大的定位误差.为解决转站过程产生的底座坐标系姿态偏差问题,本文提出基于工业相机视觉测量的环形轨道制孔系统底座位姿标定方法,通过几何建模的方式确定系统底座坐标系，建立系统手眼关系并确定视觉测量方法.在此基础上测量基准孔位,并利用Levenberg-Marquardt算法进行孔位匹配.得到实际底座坐标系在理论飞机坐标系下的位姿,并实现环形轨道制孔系统实际底座位姿的标定.

本文通过介绍环形轨道制孔系统结构及其步进式转站方法,进行系统几何建模并确立设备底座坐标系,提出基于工业相机视觉测量的底座坐标系位姿标定方法,包括系统手眼关系的建立、确定视觉测量原理、底座位姿标定原理等，进行手眼关系标定和实际底座标定实验并得出结论.

1环形轨道制孔系统

1.1环形轨道制孔系统结构及其转站方法

图1　 环形轨道制孔系统Fig.1　Circumferential splice drilling system

环形轨道制孔系统是一套新型的基于双层轨道结构和步进式转站的机身段对接区域自动化制孔设备,其外形如图1所示.机身对接区为一个360°的环形区域,要求制孔执行器必须能够精确到达该区域的任意位置.然而,在大型号飞机装配中,环形半径往往较大,制作一个覆盖360°环形区域且精度较高的轨道,不仅制造成本高、难度大,而且在使用过程中对设备的安装精度以及使用之后对设备的维护要求也很高.因此,环形轨道自动制孔系统采用“保证局部区域定位精度,移动局部区域以覆盖全部区域”的方式,将设备整体设计为双层轨道结构,并提出“步进式转站”方法,在仅需一次设备安装的情况下实现整个机身段对接区域的精确制孔.

该套系统主要由基础轨道、弧形轨道、末端执行器以及其他辅助部件组成.基础轨道位于最内侧,通过气动撑脚压紧在飞机蒙皮上以达到将设备与产品固定的目的.基础轨道精度不高,但覆盖整个360°对接区域.弧形轨道是一段可在基础轨道上运动或者固定的、圆心角约为32°的高精度轨道.末端执行器在其上运动,可实现在弧形轨道跨度范围内的精确定位,是系统的制孔执行单元,拥有6个数控运动轴共5个自由度,主要负责在弧形轨道跨度范围内的精确制孔.

环形轨道制孔系统设计成双层轨道结构,制孔时,弧形轨道与基础轨道锁定,执行器通过高精度齿轮-弧形齿条传动在弧形轨道(称为X轴)上运动,可在弧形轨道限定的区域内精确制孔,这个过程称为一个站位制孔.完成当前站位制孔任务后,将执行器先运动到弧形轨道一端,然后将其与基础轨道固定并解除弧形轨道与基础轨道的锁定关系,此时,X轴电机即可通过齿轮-弧形齿条传动反向驱动弧形轨道运动,从而实现加工区域在整个对接环形区域内的移动.这种改变加工区域位置的方法称为“步进式转站”.

1.2环形轨道制孔系统几何建模

图2　系统各运动轴示意图Fig.2　Motion axes of the system

环形轨道制孔系统几何建模原理如图2所示[8-9],该系统共有6个数控运动轴：X轴为双电机驱动,通过齿轮和弧形齿条的配合,在弧形轨道上移动,因而其运动轨迹是一段圆弧；A轴和B轴为两个旋转轴；Y轴、Z轴和进给轴均为平移轴,但由于进给轴和Z轴运动方向完全一致,并不提供独立的自由度,仅在制孔时负责主轴进给运动,不参与系统定位,因而此处在几何建模时不考虑进给轴,即最末端坐标系固结在Z轴上.

在制孔过程中,在主轴进给运动之前,安装在Z轴上的气动压脚应先推出并压紧在蒙皮表面上,以抑制震动,并通过压脚和进给轴的随动运动精确控制锪窝深度[10].压脚的最适推出距离约为15 mm,因此,系统的最末端坐标系,即Z轴坐标系原点应定义在刀具轴线上、伸出压脚外端面约15 mm的位置.这一位置称为刀具中心点(tool center point, TCP)点,对应坐标系称为TCP坐标系.当TCP坐标系与孔位坐标系重合时,即认为完成执行器运动到孔.

图3　环形轨道制孔系统坐标系系统Fig.3　Coordinate system circumferential splice drillingsystem

O0-X0Y0Z0坐标系称作底座坐标系,其原点O0位于环形轨道制孔系统的圆心,Y0轴与环形轨道中心轴线重合.当末端执行器位于X关节轴坐标零位(弧形轨道中间位置)时,做出轴线轴-A与Y0轴所在直线的公垂线,即底座坐标系Z0轴所在直线.Z0轴方向由原点O0指向执行器,通过右手定则确定X0轴.底座坐标系相对于弧形轨道位姿保持不变,当设备转站即弧形轨道运动时,底座坐标系随之一起绕Y0轴转动.

O1-X1Y1Z1坐标系用来表示A关节轴的运动,其X1轴所在直线即为A关节轴线轴-A,当末端执行器位于X轴关节零位时,该坐标系原点O1就是轴-A轴线与底座坐标系Z0轴的交点.O1-X1Y1Z1坐标系有两种运动,一方面,它随着执行器一起在弧形轨道上绕着底座坐标系Y0轴转动,转动量用θ1表示；另一方面,它随着执行器绕轴-A轴线转动,转动量用θ2表示.因此,坐标系O1-X1Y1Z1在底座坐标系O0-X0Y0Z0下的位姿用4×4齐次变换矩阵T01表示：

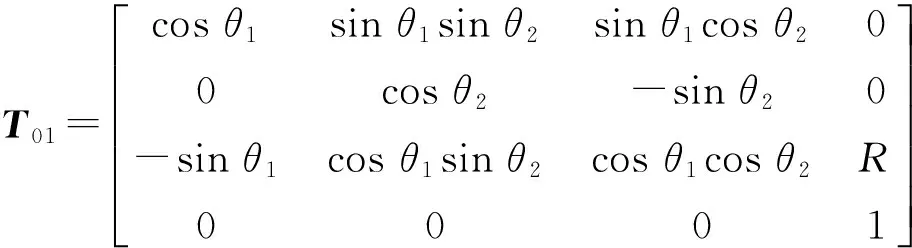
(1)

式中:R为O1、O0之间的距离,属于结构参数.

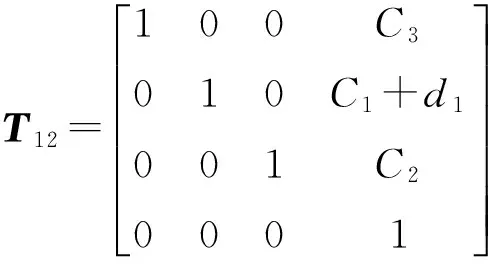
(2)

O3-X3Y3Z3坐标系用来表示B关节轴的运动,Y3轴所在直线即为B关节轴线轴-B.该坐标系与B关节轴旋转组件固结,并随之绕轴-B的轴线转动,转动量为θ3.由于原点O3可以位于轴-B直线上的任意位置,为尽量减少参数以方便运算,令原点O3位于平面X2-O2-Z2上.d2和d3分别表示原点O3相对于原点O2在X、Z方向上的偏移量,为结构参数.因此,O3-X3Y3Z3坐标系在O2-X2Y2Z2坐标系下的位姿用4×4齐次变换矩阵T23表示：

(3)

O4-X4Y4Z4坐标系用来表示Z平移轴的运动,原点O4即位于TCP点,Z4轴与Z关节轴运动方向一致.整个坐标系与Z轴拖板固结并随之运动,平移量为d7.当Z平移轴位于关节坐标零位时,d4、d5和d6就是原点O4相对于O3在Z方向上、X方向上和Y方向上的偏移量.因此,坐标系O4-X4Y4Z4在坐标系O3-X3Y3Z3下的位姿用4×4齐次变换矩阵T34表示：

(4)

综上,运动链末端TCP点上的坐标系在底座坐标系下的位姿用4×4齐次变换矩阵T04表示：

(5)

式中:R04是3×3等效旋转矩阵,P04是3×1等效平移向量.总共有6个结构参数即：R、d2、d3、d4、d5和d6,以及5个关节变量：θ1、θ2、θ3、d1和d7.

2基于视觉测量的底座坐标系位姿标定

2.1手眼关系的建立与视觉测量原理

根据1.2节可知,环形轨道制孔系统的运动链末端坐标系原点O4位于TCP点,认为相机正确安装,其光轴与刀具轴线保持平行,因此可取相机焦点处作为相机坐标系的原点,并取与TCP坐标系完全平行的方向作为相机坐标系的三轴方向,建立相机坐标系O5-X5Y5Z5.系统的手眼关系指相机坐标系O5-X5Y5Z5在TCP坐标系O4-X4Y4Z4下的位姿,如图4所示.

图4　手眼关系示意图Fig.4　Schematic diagram of Hand-eye relationship

如图4所示,由于相机安装在主轴外壳上并随进给轴一起运动,系统手眼关系将随进给轴位置的改变而改变.为使得系统手眼关系保持固定不变,相机对焦根据文献[11]的自动对焦原理,采用“进给轴不动,移动Z关节轴”的方法.在标定手眼关系前,先将进给轴运动至任意安全位置(刀尖不伸出压脚为宜)并记录该位置(如:FC),然后手动调整相机焦距,使焦点位于压脚端面以外一定合适距离(太近可能导致对焦时Z关节轴运动使压脚与飞机干涉,太远可能导致Z关节轴行程不足而无法对焦),最后定义此时的焦点位置即为相机坐标系原点O5,并按照上述方法建立相机坐标系O5-X5Y5Z5.设T45为相机坐标系O5-X5Y5Z5在TCP坐标系O4-X4Y4Z4下的齐次变换矩阵,则相机坐标系在底座坐标系下的位姿如下式所示：

(6)

式中:R05为3×3维等效旋转矩阵, P05为3×1维等效平移向量.

确定矩阵T45的过程即是系统手眼关系标定过程.完成手眼关系标定之后,在每次视觉测量之前,均应将进给轴运动到FC位置,以保证当前手眼关系与标定时一致.

确定系统手眼关系之后即可得到相机坐标系在底座坐标系下的位姿描述(式(6)).根据文献[11]给出的公式：

(7)

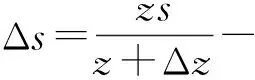
(8)

式中:Δs为由相机光轴与工件表面的不垂直和对焦的不精确产生的测量误差,z为实际物距,s为目标孔位中心点以及相机光轴与工件表面交点之间的距离,θ为孔轴线与相机光轴的夹角,Δz为物距的变化量.

通过迭代测量的方法,即不断对焦和对中(使得目标孔位中心处于视野中心),s将趋于零,能够最大程度消除测量误差Δs.因此,环形轨道自动制孔系统视觉测量也采用迭代测量的方法,通过不断对焦对中,使得相机坐标系原点与孔位中心重合.此时通过计算相机坐标系在底座坐标系下的位姿,即可得到当前孔位在底座坐标系下的位置,这就是视觉测量的基本原理.然而,由于测量时无法保证相机光轴与孔中心轴线高度重合,因此视觉测量仅可以得到目标孔位在底座坐标系下的位置信息,无法得到方向(姿态)信息.

2.2环形轨道制孔系统底座坐标系位姿标定

在环形轨道制孔系统加工过程中,由于受弧形轨道限定的执行器可加工区域范围有限,需要移动弧形轨道,从而改变执行器可加工区域在整个圆周上的位置,这个过程称作转站.

当弧形轨道切换到一个新的站位之后,由于制造、安装以及转站运动产生的误差,实际底座坐标系相对于飞机坐标系的位置有所偏差.而且转站后的底座坐标系相对于之前的底座坐标系也并不仅仅只是绕着Y0轴转动了一个角度,而是极有可能在其他2个轴以及原点的位置上也有所偏差.因此,为了获得较准确的当前底座坐标系在飞机坐标系下的位姿,需要对底座坐标系位姿进行重新确定,即环形轨道制孔系统底座坐标系位姿标定,也称作设备建站.

机身对接区域的孔主要分为两种类型：预制基准孔和待加工孔.其中,待加工孔指的是需要环形轨道制孔系统制出来的孔,而预制基准孔是在设备安装之前人工预先制好的孔位.通过测量这些基准孔的实际坐标,并与离线文件中的理论坐标值进行对比,得到每个基准孔位的偏差值,然后利用这些偏差值通过双线性插值的方法得到待加工孔的实际坐标值,这个过程称作孔位修正[12].基准孔的另一个功能就是作为底座坐标系位姿标定的基准使用,如图5所示.

图5　底座坐标系标定示意图Fig.5　Diagram for base frame calibration

在离线仿真中,可以直接获得这些孔位在飞机坐标系下的理论位姿,并可读出当前站位底座坐标系在飞机坐标系下的理论位姿.然而,通过环形轨道制孔系统视觉测量得到的却是这些孔位在实际底座坐标系下的位置,因此底座坐标系位姿标定就是指确定当前实际底座坐标系OD-XDYDZD和离线仿真中的理论飞机坐标系OA-XAYAZA之间的关系.

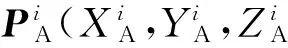
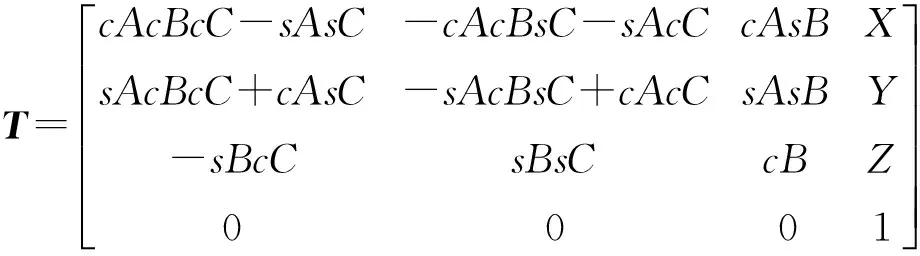
(9)

(cA→cosA,cB→cosB,cC→cosC,

sA→sinA,sB→sinB,sC→sinC)

在式(9)中,用R表示旋转矩阵,用P表示平移向量,则有

(10)

(11)

则当R和P为实际底座坐标系在理论飞机坐标系下的描述时,有

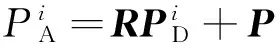
(12)

因此可得最小二乘问题的目标方程为

(13)

由于R和P可由X,Y,Z,A,B,C得出,需要优化的参数就是X、Y、Z、A、B、C,其迭代初值可直接从离线编程仿真中读出,采用Levenberg-Marquardt非线性优化算法[13-15]可求出最优结果.

3实验环节

3.1手眼关系标定

图6　单孔标定手眼关系示意图Fig.6　Schematic diagram of Hand-eye relationship based on calibration

因此,原制孔时的TCP坐标系在当前测量时的TCP坐标系下的位姿可以表示为

(14)

式中：TC为测量时TCP坐标系在底坐标系;T1的位姿,Td为钻孔的TCP坐标系在底座坐标系下的位姿,ΔR为等效3×3维旋转矩阵，ΔP为等效3×1维平系的向量.

由于此时的相机坐标系原点和钻孔时的TCP坐标系原点重合,ΔP即是所需要的手眼关系中的平移向量,进而可以得到手眼关系的齐次变换矩阵.

根据上述原理,在工件板上钻孔,并记录TCP坐标系在底座坐标系下的齐次变换矩阵：

Td=

先将进给轴运动至2.1节所述的FC位置,此处FC=-50.0,然后进行相机对焦-对中迭代测量,直到目标孔位中心完全处于相机视野中心为止,如图7所示.记录此时TCP在底座坐标系下的位姿：

TC=

图7　视觉测量软件截图Fig.7　Screan shot of vision measurement software

因此,最终手眼关系矩阵中的平移向量为[8.727,-97.044,-27.470].

3.2底座坐标系位姿标定

根据上述底座坐标系位姿标定原理,从离线仿真模型中获取预制基准孔在理论飞机坐标系下的坐标值以及理论底座坐标系在理论飞机坐标系下的位姿.通过视觉测量系统测出实际预制基准孔在实际底座坐标系下的坐标值,利用Levenberg-Marquardt算法进行点位匹配得到实际底座坐标系在理论飞机坐标系下的位姿,完成底座坐标系位姿标定.其中,Levenberg-Marquardt算法迭代的初值即为理论底座坐标系在理论飞机坐标系下的位姿.

实验数据如下表1～2所示：其中,表1为6个基准孔在理论飞机坐标系下的坐标值,直接从离线仿真中获得;表2为上述6个基准孔在实际设备底座坐标系下的坐标值,通过视觉测量获得.

表1飞机坐标系下基准孔的理论坐标值

Tab.1Nominal coordinates of reference holes in aircraft coordinate system

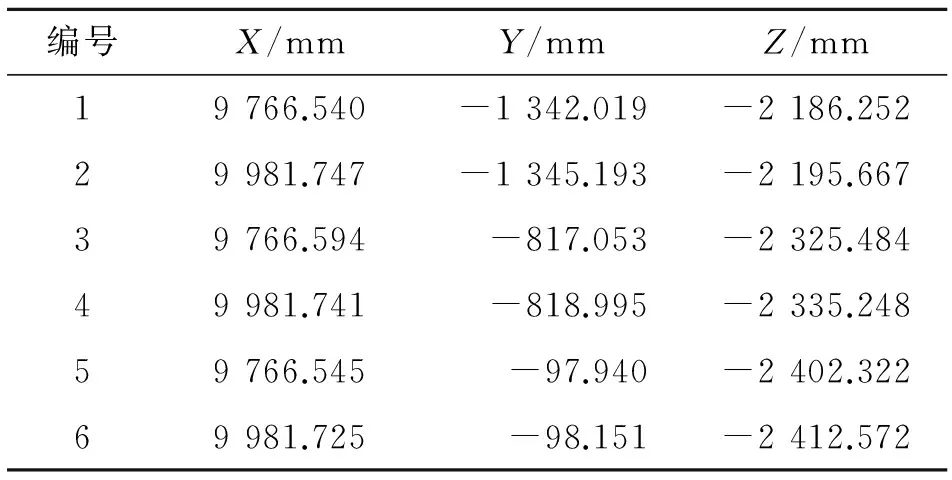
编号X/mmY/mmZ/mm19766.540-1342.019-2186.25229981.747-1345.193-2195.66739766.594-817.053-2325.48449981.741-818.995-2335.24859766.545-97.940-2402.32269981.725-98.151-2412.572

表2底座坐标系下基准孔的实际坐标值

Tab.2Actual coordinates of reference holes in base frame

编号X/mmY/mmZ/mm1-607.686-51.7572486.1292-606.856160.9232494.8903-65.146-53.6522458.3414-63.264161.7752471.0235641.748-53.4492313.5166646.651159.2782325.957

从离线仿真系统可以直接获得设备底座坐标系在理论飞机坐标系下的位姿,记为X0,Y0,Z0,A0,B0,C0]=[9 825.021, 0, 0.255, -90, 71.957,-90]可将具作为这代初值.优化得到最终实际底座坐标系在理论飞机坐标系下的位姿：[X,Y,Z,A,B,C] = [9 803.196,-9.965,-1.790,-88.665,162.362,1.414].将该关系重新代入系统,通过基准孔在理论飞机坐标系下的位置计算得到基准孔在实际底座坐标系下的位置并和实测值进行对比,比较结果如图8所示：

X误差、Y误差和Z误差分别表示X、Y和Z向的偏差,称为建站误差.横坐标i取值为1～6,是基准孔的编号.可以看出,建站误差较小,即这种底座标定方法可以较准确地标定出实际底座坐标系在理论飞机坐标系下的位姿,为下一步孔位修正[12]打好基础.

图8　底座位姿标定误差Fig.8　Calibration error of base frame

4结语

本文以浙江大学自主研制的专用于大型飞机机身对接段区域的环形轨道制孔系统为基础,通过对系统运动建模,确定系统底座坐标系和手眼关系,并进一步确定视觉测量原理.通过视觉测量得到机身预制基准孔在实际底座坐标系下的坐标,并利用Levenberg-Marquardt算法将其和理论坐标值进行匹配,从而实现利用低成本的工业相机实现环形轨道制孔系统相对高精度的底座坐标系姿态标定的目的.实验结果验证了本文提出的底座坐标系标定方法的可行性.

由于飞机机身半径较大，导致一个站位的运动距离也比较大，执行器需要进行几乎覆盖整个站位区域的运动才能测完所有的建站基准孔，这严重制约着整个底座标定过程的效率.后续研究应该尽可能提高设备的制造、安装精度和产品的装配、调姿精度，同时通过研究转站定位方法以设法提高设备转站过程的定位精度，从而保证转站完成后，实际底座坐标系在理论飞机坐标系下的位姿接近于仿真理论值，进而可以免去底座标定过程，大大提高设备工作效率.

参考文献(References)：

[1] 王彬.飞机大部件数字化自动对接装配技术研究[J].航空工程进展,2013,4(1): 134-138.

WANGBin.Researchondigitalautomaticdockingassemblytechnologyofaircraftstructuralparts[J].AdvancesinAeronauticalScienceandEngineering, 2013,4(1): 134-138.

[2] 卜泳,许国康,肖庆东.飞机结构件的自动化精密制孔技术 [J]. 航空制造技术,2009(24)： 61-64.

BUYong,XUGuo-kang,XIAOQing-dong.Automaticprecisiondrillingtechnologyofaircraftstructuralpart[J].AeronauticalManufacturingTechnology, 2009(24): 61-64.

[3]DEVLIEGR.Expandingtheuseofroboticsinairframeassemblyviaaccuraterobottechnology[J].SAEInternationalJournalofAerospace, 2010, 3(1): 198-203.

[4]DEVLIEGR,SITTONK,FEIKERTE,et.al.ONCE(One-sidedCellEndeffector)roboticdrillingsystem[J].SAETechnicalPaper, 2002(1): 2626.

[5]ATKINSONJ,HARTMANNJ,JONESS,etal.Roboticdrillingsystemfor737aileron[J].SAETechnicalPaper, 2007: 01-3821.

[6]OLSSONT,HAAGEM,KIHLMANH,et.al.Cost-efficientdrillingusingindustrialrobotswithhigh-bandwidthforcefeedback[J].RoboticsComputer-IntegratedManufacturing, 2010, 26(1): 24-38.

[7]DEVLIEGR.High-accuracyroboticdrilling/millingof737 [J].SocietyofAutomotiveEngineers, 2011, 4(2): 1373-1379.

[8]ZHUWD,MEIB,KEYL.Inversekinematicssolutionofanewcircumferentialdrillingmachineforaircraftassembly[J].Robotica, 2014, 34(1): 1-20.

[9]ZHUWD,MEIB,KEYL.Kinematicmodelingandparameteridentificationpofanewcircumferentialdrillingmachineforaircraftassembly[J].InternationalJournalofAdvancedManufacturingTechnology, 2014, 72(5-8): 1143-1158.

[10] 费少华,方强,孟祥磊,等. 基于压脚位移补偿的机器人制孔锪窝深度控制[J]. 浙江大学学报：工学版,2012,46(7)： 1157-1161.FEIShao-hua,FANGQiang,MENGXiang-lei,et.al.Countersinkdepthcontrolofrobotdrillingbasedonpressurefootdisplacementcompensation[J].JournalofZhejiangUniversity：EngineeringScience, 2012, 46(7): 1157-1161.

[11]ZHUWD,MEIB,YANGR,et.al.Measurementerroranalysisandaccuracyenhancementof2Dvisionsystemforroboticdrilling[J].RoboticsandComputer-IntegratedManufacturing, 2014, 30(2): 160-171.

[12]ZHUWD,QUWW,CAOLH,et.al.Anoff-lineprogrammingsystemforroboticdrillinginaerospacemanufacturing[J].InternationalJournalofAdvancedManufacturingTechnology, 2013, 68(9-12): 2535-2545.

[13]MADSENK,NIELSENHB,TINGLEFFO.Methodsfornon-linearleastsquaresproblems[J].SiamJournalonOptimization, 2004, 16(1): 487-490.

[14] 张鸿燕,耿征.Levenberg-Marquardt算法的一种新解释 [J]. 计算机工程与应用,2009,45(19): 5-8.

ZHANGHong-yan,GENGZheng.NovelinterpretationforLevernberg-Marquardtalgorithm[J].ComputerEngineeringandApplication. 2009, 45(19): 5-8.

[15]MACF,JIANGLH.SomeresearchonLevenberg-Marquardtmethodforthenonlinearequations[J].AppliedMathematicsandComputation, 2007, 184(2): 1032-1040.

收稿日期：2015-07-12.

基金项目：国家自然科学基金资助项目(51205352).

作者简介：张阿龙(1990—),男,硕士生,从事机械制造及其自动化研究. ORCID： 0000-0001-5993-8755. E-mail: zalzju@qq.com 通信联系人：朱伟东,男,副教授,博士. ORCID: 0000-0003-4067-1450. E-mail: wdzhu@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.06.010

中图分类号：TP 242.3

文献标志码：A

文章编号：1008-973X(2016)06-1080-08

Base frame calibration of circumferential splice drilling system based on visual measurement

ZHANG A-long1, ZHANG Ming1, QIAO Ming-jie2, ZHU Wei-dong1, MEI Biao1

(1.DepartmentofMechanicalEngineering,ZhejiangUniversity,Hangzhou310027,China;2.AVICXi’anAircraftIndustry(Group)Co.Ltd,Xi’an710089,China)

Abstract:A new base frame calibration method based on visual measurement was proposed and demonstrated in order to improve the positioning accuracy of the circumferential splice drilling system after automatic stepping process, and to eliminate the impact of errors caused by manufacturing, assembly, installation and motion. By establishing the kinematic model and hand-eye relationship of the system, a coordinate system of the equipment from base to camera was set up, which determined the visual measurement principle. With this principle, some prefabricated benchmark holes were measured and the relationship between actual base frame and theoretical aircraft coordinate systems could be achieved by using hole-matching method based on Levenberg-Marquardt least squares fitting algorithm. Experimental results show that the proposed base frame calibration method based on visual measurement could achieve the accuracy within 2 mm, which totally meets the requirement of base frame calibration. The results also reveal correctness and convenience of the proposed method.

Key words:circumferential splice drilling system; kinematic model; visual measurement; least squares fitting method; base frame calibration; Levenberg-Marquardt