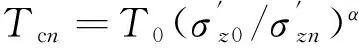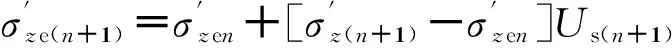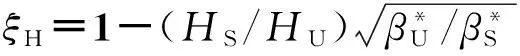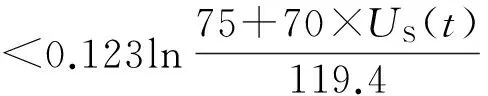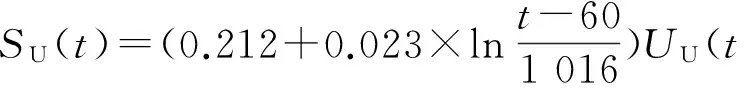Yin-Graham流变模型沉降简化计算统一公式
胡亚元, 杨秋华
(浙江大学 滨海和城市岩土工程研究中心,浙江 杭州 310027)
Yin-Graham流变模型沉降简化计算统一公式
胡亚元, 杨秋华
(浙江大学 滨海和城市岩土工程研究中心,浙江 杭州 310027)
摘要:从准塑性黏弹性模型在一定条件下假说B与修正的假说A近似等价的视角出发,基于Yin-Graham等效时间流变模型,通过时间折减因子修正实际时间和等效时间之间的差异,提出用等效时间表示的新孔隙比简化计算公式.该公式适用于任意突然加卸载工况,包括加载到正常固结土、加载到超固结土、卸载和卸载再加载.通过总固结度法和分级固结度法获得2种多级加载孔隙比简化计算公式.与精确解和现场实测数据对比结果表明,单级加载时新孔隙比简化公式预测的工后沉降计算偏差明显低于采用经典法和旧等效时间法得到的计算偏差;多级加载时总固结度法和分级固结度法计算的理论超载预压持续时间和工后沉降量均与精确解结果接近;由于总固结度法远比分级固结度法简单,建议采用前者计算预压法工艺的持续时间和工后沉降量.
关键词:孔隙比;主次固结沉降;简化计算公式;计算偏差;堆载预压
随着国民经济的发展,基础设施对工后沉降的要求越来越高[1-3].当采用预压法加固地基时,尽管其加固参数是根据工后沉降要求设计的,但仍有相当一部分软土地基的实际工后沉降超出了设计预期,造成高速公路、机场路面开裂和工后沉降过大等现象[4-5].一些研究软土黏性力学的专家认为,经典土力学中考虑次固结变形的沉降计算公式低估了软土的实际沉降是造成这一缺陷的重要因素之一[6-8].为了克服这一缺陷,Yin等[9-13]建立了能够考虑黏性变形的本构方程,用于软土地基的固结和沉降分析.殷建华等[6-7,14-15]基于Bjerrum等时蠕变图[16]提出了确定软土地基次固结沉降开始时间的新思路.由于Bjerrum等时蠕变图包含了软土的主次固结变形,通过推广Bjerrum蠕变图中等时间线概念而获得的Yin-Graham等效时间流变模型[9]受到了一些岩土专家的青睐.Zhu等[17]利用Yin-Graham流变模型[9]分析了加拿大Berthierville试验堤坝的固结特性和沉降规律.Nash等[18]利用小应变砂井轴对称固结模型和Yin-Graham流变模型[9]模拟了第二塞文立交桥附近高速公路路基堆载预压的现场实测数据,结果表明,采用传统次固结理论将导致预压时间不足和工后沉降超出预期等缺陷.笔者[19]采用大应变砂井固结模型和Yin-Graham流变方程分析了香港-深圳西部港湾填海工程的预压持续时间和工后沉降量,获得了与文献[18]相一致的结论.然而,虽然这些成果能够较合理地估计软土主次固结沉降的发展过程,但Yin-Graham流变模型是非线性本构方程,因此需要编制复杂的有限元或差分程序才能实现预测软土固结沉降的目的;一些能够解析获得次固结沉降量的研究成果又只适用于恒有效应力条件[7,14-15],与预压法中有效应力随固结度增大的现状差别较大.上述种种缺陷极大地限制了Bjerrum等时蠕变图和Yin-Graham流变模型在工程中的应用.
本文的研究目的是从准塑性黏弹性模型的假说B与修正的假说A近似等价的性质出发[14],采用有效时间概念提出新的沉降简化公式,使其与Yin-Graham模型一样既能反映主次固结变形在一定条件下可以相互转化的性质[7,14],也能在一定程度上反映有效应力变化引起的实际时间与等效时间之间的差异.当不考虑流固耦合以及实际时间与等效时间之间的差异时,殷建华[6]提出的上述4种工况的沉降简化公式是本文沉降简化公式的近似式.把本文获得的沉降简化公式按照总固结度法和分级固结度法这2种方法从单级加载推广到多级加载,分别提出各个加载阶段的沉降简化公式,用于堆载预压持续时间设计和工后沉降量预测.在事例分析中,利用宁波某机场堆载预压工艺参数[2,20],把经典法[21]、文献[6]所述方法和本文的单级孔隙比简化计算公式获得的沉降与精确解获得的沉降[22]进行对比分析,结果表明,堆载预压难以达到设计要求的工后沉降.利用总固结度法和分级固结度法多级加载沉降简化公式分析该机场超载预压工程的理论持续时间,预测按实际持续时间卸载后的工后沉降量,并与精确解理论结果[22]和实测值[2,20,22]进行对比,分析这2种多级加载沉降简化公式产生计算误差的成因,以促进考虑次固结的堆载预压简化设计方法的完善和实用化进程.
1一维应变的孔隙比简化计算公式
本文采用孔隙比代替沉降来反映外荷载突然作用下土单元的一维应变竖向变形.本节先不考虑由于有效应力变化引起的实际时间和等效时间之间的差异,获得一维应变的孔隙比简化计算公式.在此基础上,通过引入时间折算因子反映实际时间与等效时间之间差异对孔隙比变化量的影响.
1.1单级加载的孔隙比简化计算公式
在突然施加外荷载条件下,经典土力学中土单元孔隙比在固结过程中的简化计算公式[6,21]为
(1)
式中:efp为最终主固结孔隙比变化量,U(t)为固结度,tEOP为主固结完成时间,eb为加载前孔隙比,ψ为次固结系数.殷建华[6]基于流变力学假说B理论,把式(1)推广到在主固结阶段考虑次固结的土单元孔隙比简化计算公式:
eh(t)=eb-efpU(t)-efc.
(2)
式中:efc为最终(U(t)≡100%)次固结孔隙比变化量.文献[6]针对加载到正常固结土、加载到超固结土,卸载和卸载再加载4种工况,分别给出了efc的具体计算公式[6].
然而,殷宗泽等[7]指出土体的主次固结变形在一定条件下可以相互转化.笔者根据准塑性的黏弹性理论证明了主固结变形中塑性变形和次固结变形均属于流变变形,这些不但发生在整个固结过程中,而且数值会随着选择不同绝对等效时间上的前期固结压力而呈现此消彼长的变化[14].为了反映主次固结可以相互转化的性质,主次固结变形与固结度之间的耦合作用应当具有相同的形式,式(2)只对主固结最终孔隙比变化量按固结度进行折减难以满足这一要求,应当同时对最终次固结孔隙比变化量按固结度进行折减.文献[6]中的次固结沉降计算公式是基于恒有效应力条件获得的.事实上,有效应力在固结期间是随着固结度的增加逐渐增长的,把次固结沉降近似地视为瞬时加载后维持恒载发展是一种近似地简化算法,高估了主固结阶段的次固结沉降量,从这个视角考虑,也需要对式(2)中的最终次固结孔隙比变化量按固结度进行折减.因此,本文建议的孔隙比简化计算公式为
eh(t)=eb-(efp+efc)U(t).
(3)
设土体的压缩指数、回弹指数和次固结系数分别是λ、κ和ψ.定义黏塑性系数为
α=(λ-κ)/ψ.
(4)
定义绝对等效时间为T=Tr+te[14,22],te为Yin和Graham所定义的相对等效时间[6,9,17-18],Tr为参考等效时间,如图1所示.

图1 Bjerrum蠕变图Fig.1 Bjerrum’s creep diagram

(5)
令

(6)
把式(6)代入到式(5)得
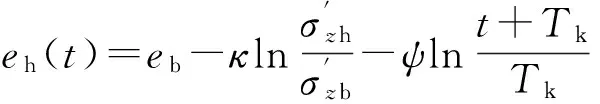
(7)
把U(t)≡100%和式(7)代入到式(3)得

(8)
把式(8)代入式(3)可获得单级加载固结过程中t时刻的孔隙比简化计算公式为
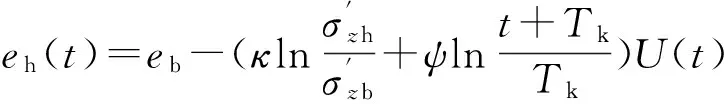
(9)
利用式(6),式(9)还可以转换为

(10)
由于在根据Yin-Graham流变模型推导式(8)过程中除单级瞬时加载外未对土体的初始和最终应力状态进行任何限制,文献[6]获得的加载到正常固结土、加载到超固结土、卸载以及卸载再加载四种工况的主次固结变形公式应当是本文公式的特例或近似式.下文将证明这一结论.


(11)

(12)
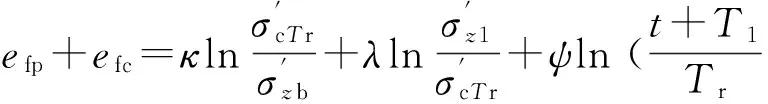
(13)

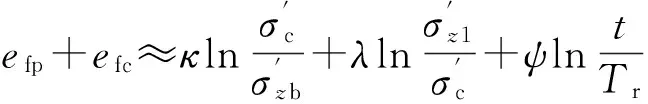
(14)
故根据式(13)~(14)可知,式(9)包含了主次固结变形.其中,
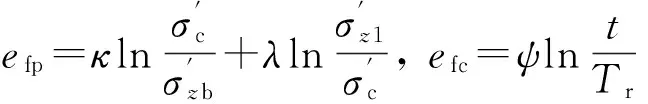
(15)
如果把文献[6]中加载到正常固结状态时的主次固结变形公式[文献[6]中的式(33a)、式(34b)和式(35b)]写成与本文一致的符号,则可发现其与本文的式(15)是一致的.故式(8)近似包含了加载到正常固结土工况的主次固结变形公式.

(16)

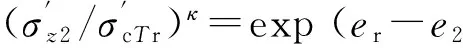
(17)
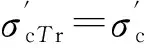

(18)
由于超固结土的最终主固结变形为弹性变形,即:

(19)
超固结土最终次固结变形由式(8)和式(19)得
efc=ψln[(t+T2)/T2].
(20)
如果把文献[6]中加载到超固结状态时的主次固结变形公式写成与本文一致的符号,则主固结变形公式与本文一致,次固结变形有细微差别,文献[6]中的式(36a)的次固结部分根据式(19)可得
efc=ψln [(t+T2-Tr)/T2].
(21)
式(21)与式(20)相比,对数函数中的分子式多减了一个Tr.Yin-Graham流变模型的弹性压缩线是瞬时时间线,对应的是t=0的情况[9,14].在式(21)中对应的是t=Tr的情况,这说明式(21)是一个近似式.但由于预压法地基处理设计时t的取值远远大于Tr,即t≫Tr,故式(21)与式(20)计算值之差是微乎其微的,完全可以忽略不计.
式(8)还可以退化到文献[6]中的卸载、卸载再加载这2种工况下的沉降简化公式,由于整个推导大同小异,受篇幅限制不再具体推导.
1.2考虑时间折减效应的孔隙比简化计算公式
对于Yin-Graham流变模型,只有在维持恒载的条件下,实际时间才等于等效时间.在预压法地基中,有效应力是随着固结度逐渐增加的,因此实际时间并不等于等效时间,引入时间折减因子β来反映实际时间与等效时间之间的差异,把式(9)~(10)进一步修正为

(22)
或

(23)
笔者通过多个工程实例把沉降简化近似公式的计算结果与精确解进行对比分析,β的取值对沉降的影响相对较小,当构筑物对工后沉降要求不高时可以忽略两者之间的差别,取β=1.但当构筑物对工后沉降要求较严时,β可按经验取值,如表1所示.事实上,式(22)(或式(23))与式(9)的计算值相比最大不超过ψln(1/β),由于1≤1/β≤2,ψ约为(0.03~0.06)λ[14],因此式(9)与式(22)(或式(23))的计算值实际上相差是比较小的.
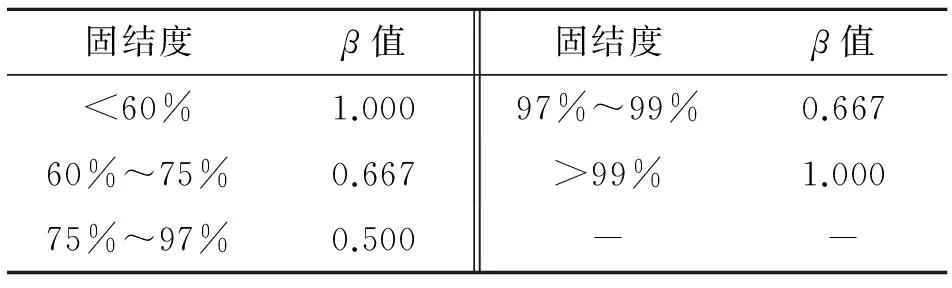
表1 时间折减因子的经验取值
2多级加载的孔隙比简化计算公式
2.1总固结度法的多级加载孔隙比简化计算公式
由于在预压法地基处理中通常采用多级加载预压方法,为了方便沉降简化公式的应用,将其从单级加载推广到多级加载工况.
多级加载时固结期间的孔隙比随时间变化的简化计算公式根据研究思路的不同可分为总固结度法和分级固结度法.总固结度法以第一级加载时的有效应力作为起始有效应力来计算总主固结孔隙比变化量和总次固结孔隙比变化量.分级固结度法把多级加载分为n个单级加载,分别计算每一级加载的主次固结孔隙比变化量.本节先研究总固结度法的孔隙比简化计算公式.

图2 多级加载计划Fig.2 Multi-stage loading schedule


要获得各级固结期间孔隙比随时间的简化计算公式,根据总固结度法的定义,首先要推求各级荷载作用下从第一级加载开始起算的主次固结最终孔隙比变化量之和.通过逐级应用式(8),可获得第n级主次固结孔隙比变化量之和为(当n (24) 式中: (25) (26) 借鉴单级加载的孔隙比简化计算公式,第n级加载后t时刻土单元的孔隙比简化计算公式写为 (27) 2.2分级固结度法的多级加载孔隙比简化计算公式 设tv=t-tn-1,Un(tv)是从第n级加载开始起算的固结度.在式(27)中,下一级的主次固结孔隙比变化量是按照本级固结度Un(tv)达到100%条件进行换算的,但在实际工程中下一级加载时本级固结度未达到100%,因此需要研究此时的多级加载孔隙比简化公式. ee(n+1)= (28). 式中: (29) 根据固结度的应力定义可知第n+1级结束时的有效应力为 (30) (31) 3实例分析 文献[2]总结了根据Terzaghi固结理论获得的固结度公式,认为可以统一地写为以下形式[21]: (32) (33) 式中:HS为砂土加固区的厚度.对于瞬时多级加载,按第一级加载开始起算的固结度计算公式[2,21]为 (34) 式中:Δσzm=σzm-σz(m-1).第n级加载开始时孔压为 再经过时间tv后的孔压由式(34)得 故从第n级加载开始起算的固结度公式为 (35) t时刻地基中每一土层沉降与孔隙比之间的关系为 (36) 式中:i=S指砂井加固层,i=U为下卧层,下同. 3.1等载预压的工后沉降分析 由于下卧层固结较慢,本场地平均固结度达到80%时预压期已达300 d.从表2中可以看出,若采用等载预压,地基平均固结度达到80%时的工后沉降即使按预测值最小的经典法考虑也达到0.188 m,远大于0.080 m的工后沉降设计要求,因此,需要采用超载预压来降低其工后沉降和缩短预压时间. 3.2超载预压设计 由于满足工后沉降设计要求的等载预压期过长,需要对该工程进行超载预压加固.设超载量ps=25.6 kPa,预压荷载为pf+s=70 kPa,堆载计划如图3所示[2,20,22],折算成突然加载的分级堆载计划见图3中的虚线:共2级堆载,第1级堆载Δσz1=35 kPa,持续60 d后第2级再加载Δσz2=35 kPa,预压加固工艺要求知道第2级需要预压多少天才能达到工后沉降小于0.08 m的要求.本工程第2级实际有效的恒载预压持续时间为210 d(见图3虚线),预压卸载后的工后沉降是多少. 表2 简化方法与精确解工后沉降对比表 注:平均固结度指的是包括砂井层和下卧层整个地基的固结度,工降指的是工后沉降,偏差指的是工后沉降计算偏差. 图3 宁波机场预压堆载计划Fig.3 Surcharge preloading plan in project of Ningboairport 根据式(36)可得砂井加固层的沉降SSf为 Sf=SSf+SUf=0.894 m. (37) 1)按2.1节介绍的总固结度法进行预压设计. Tc2=1 016×(75/145)26.39, Ts2=1 016×(75/145)26.39+60×(110/145)26.39. 砂井加固层多级加载的固结度公式根据式(34)得 US(t)=1-1.322exp (-0.013 6t). 由于Ts2≈0,故β2(t-t1)+Ts2≈β2(t-t1),t1=60 d,卸载时砂井加固层的固结度大于75%,按表1取β2=0.5,由式(27)和式(36)得固结期间沉降随时间变化公式: (38) (39) 式中:〈x〉为Macauley函数:当x≥0时,〈x〉=x;当x<0时,〈x〉=0. 同理,下卧层的固结度公式为 UU(t)=1-0.849exp (-0.001 52t).下卧层固结期间的沉降随时间变化公式为(由于下卧层卸载时的固结度小于60%,按表1取β2=1): (40) 卸载时下卧层的回弹变形为 (41) 地基的总变形为砂井加固层和下卧层变形之和.对于超载预压,卸载时的临界沉降等于最终沉降减去工后沉降加上超载引起的回弹沉降,由此得 SS+SU=Sf-[SG]+SSs+SUs. (42) 把式(37)~(41)和[SG]=0.08 m代入式(42)后求解式(42)可得t=310 d,故需要预压310 d,即第二级荷载需持续250 d才能满足工后沉降小于0.08 m的要求.按照精确解获得的满足工后沉降要求的预压持续时间为325 d(第二级堆载预压时间为265 d)[23],比总固结度法计算的预压持续时间大15 d;本工程第二级实际只预压了210 d,根据与计算持续时间类似的步骤,按总固结度法预测得到的工后沉降为0.106 m.比工艺要求的工后沉降大0.026 m.现场实测的工后沉降为0.160 m,按总固结度法预测的工后沉降比实测沉降小0.054 m,造成这一误差的原因是Yin-Graham流变模型是非线性模型,因此把土层的中心点作为应变平均值所在点是一种近似处理方法. 2)按2.2节介绍的分级固结度法进行预压设计. (43) 根据式(35),按第2级起算时的砂井层固结度公式为 US2(tv)= 1-0.861exp (-0.0136tv). (44) 第2级有效应力随时间变化公式为 则卸载时砂井层的回弹沉降为 (45) (46) 式中:UU2(tv)为下卧层按第2级起算的固结度 UU2(tv)=1-0.891exp (-0.001 52tv). (47) 卸载时整个地基的临界沉降等于最终沉降减去工后沉降加上超载引起的回弹沉降,由此得 SS2+SU2=Sf-[SG]+SSs+SUs. (48) 把式(43)~(47)代入到式(48)后求解式(48)可得tv=260 d,即第二级的预压持续时间为260 d,预压总持续时间为60+260=320 d,而按照精确解计算的满足工后沉降要求的预压持续时间为325 d(第二级堆载预压时间为265 d)[23],比分级固结度法计算的预压持续时间大5 d.本工程第二级实际只预压了210 d,根据2.2节分级固结度法预测的工后沉降为0.108 m.现场实测的工后沉降为0.160 m.比分级固结度法预测的工后沉降大0.052 m.与总固结度法类似,造成这一误差的原因是Yin-Graham流变模型是非线性模型,因此把土层的中心点作为应变平均值所在点是一种近似处理方法. 从上述多级加载孔隙比简化公式分析超载预压持续时间和工后沉降看,总固结度法和分级固结度法两者的计算结果比较接近.从算例的整个分析过程可以看出,产生这一结果的原因是当土体有效应力经预压荷载作用超过前期固结压力后,决定次固结变形大小的绝对等效时间数值受前几级预压持续时间和初始绝对等效时间的影响较小,而主要受最后一级预压持续时间的影响,文献[22]也得出与这相同的结论.因此按总固结度法和分级固结度法多级加载孔隙比简化公式这2种方法获得的预压分析结果就比较接近了.由于总固结度法远比分级固结度法简单,建议采用前者计算预压法工艺的持续时间和工后沉降量. 4结论 (1)基于Yin-Graham流变模型,获得了单级加卸载条件下孔隙比简化计算公式.该简化公式的最终主次固结沉降统一了文献[6]中的简化公式中加载到正常固结土、加载到超固结土、卸载和卸载再加载4种工况下的4个沉降简化计算公式.同时,本文还通过引入时间折减因子考虑了有效应力变化时实际时间和等效时间之间的差异,提高了孔隙比简化计算公式的精度. (2)在固结度服从文献[2]提出的普遍公式的假定下,针对某工程实例,把本文单级加载沉降简化计算公式、殷建华公式(旧等效时间法)、经典土力学提供的沉降简化计算公式一起与精确解进行了对比研究,结果表明,当平均固结度介于50%~95%时,这3种简化方法中经典法的计算偏差最大,文献[6]的方法计算偏差次之,本文方法的计算偏差最小. (3)根据堆载预压多级加载的特点,提出总固结度法孔隙比简化计算公式和分级固结度法孔隙比简化计算公式.利用总固结度法和分级固结度法这两种多级加载孔隙比简化计算公式对某工程的超载预压持续时间和工后沉降进行了理论计算,并与精确解获得的结果和实测值进行了比对.结果显示,两者所获的结果基本一致,均可作为孔隙比简化计算公式用于多级加载预压法的简化设计. 参考文献(References): [1] 中国人民共和国铁道部.高速铁路设计规范(试行):TB10026-2009 [S]. 北京:中国标准出版社, 2009. [2] 龚晓南.地基处理手册:第三版[M].北京:中国建筑工业出版社, 2008: 69-162. [3] 中华人民共和国交通运输部.公路软土地基路堤设计与施工技术规范:JTG/T D31-02-2013[S]. 北京:中国标准出版社, 2013. [4] 刘汉龙,扈胜霞,ALI Hassan.真空-堆载预压作用下软土蠕变特性试验研究[J].岩土力学,2008, 29(1): 6-12. LIU Han-long, HU Sheng-xia, ALI H. Test study on creep characteristics of soft clayey soils under consolidation by vacuum-surcharge combined preloading method [J]. Rock and Soil Mechanics, 2008, 29(1): 6-12. [5] 郭林, 蔡袁强,谷川,等.循环荷载下软黏土回弹和累积变形特性[J].浙江大学学报:工学版, 2013,47(12): 2111-2117. GUO Lin, CAI Yuan-qiang, GU Chuan, et al. Resilient and permanent strain behavior of soft clay under cyclic loading [J]. Journal of Zhejiang University: Engineering Science, 2013, 47(12): 2111-2117. [6] 殷建华.从本构模型研究到试验和光纤监测技术研发[J].岩土工程学报,2011, 33(1): 1-15. YIN Jian-hua. From constitutive modeling to development of laboratory testing and optical fiber sensor monitoring technologies [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 1-15. [7] 殷宗泽,张海波,朱俊高,等.软土的次固结[J].岩土工程学报,2003, 25(5): 521-526. YIN Zong-ze, ZHANG Hai-bo, ZHU Jun-gao, et al. Secondary consolidation of soft soils [J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 521-526. [8] DEGAGO S A, GRIMSTAD G, JOSTAD H P, et al. Use and misuse of the isotache concept with respect to creep hypotheses A and B [J]. Geotechnique, 2011,61(10): 897-908. [9] YIN J H, GRAHAM J. Viscous-elastic-plastic modelling of one-dimensional time-dependent behaviour of clays [J]. Canadian Geotechnical Journal, 1989, 26(2): 199-209. [10] SHI J Y, ZHAO W B, LI F H. Settlement analysis for an embankment considering visco-elasto-plastic characteristics [J]. China Ocean Engineering, 2000, 14(3): 349-360. [11] YIN J H, ZHU J G, GRAHAM J. A new elastic visco-plastic model for time-dependent behaviour of normally and overconsolidated clays-theory and verification [J]. Canadian Geotechnical Journal, 2002, 39(1): 157-173. [12] 谢新宇,李金柱,王文军,等.宁波软土流变试验及经验模型[J].浙江大学学报:工学版,2012, 46(1): 64-71. XIE Xin-yu, LI Jin-zhu, WANG Wen-jun, et al. Rheological test and empirical model of Ningbo soft soil [J]. Journal of Zhejiang University: Engineering Science, 2012,46(1): 64-71. [13] 张超杰,王立忠,陈云敏.一维弹粘塑性固结模型及其应用[J].浙江大学学报:工学版,2003, 37(1): 10-15. ZHANG Chao-jie, WANG Li-zhong, CHEN Yun-min. One-dimensional elastic viscoplastic consolidation model and its application [J]. Journal of Zhejiang University: Engineering Science, 2003, 37(1): 10-15. [14] 胡亚元.考虑蠕变时预压期的近似确定方法[J].浙江大学学报:工学版,2012, 46(2): 250-256. HU Ya-yuan. Approximately determining preloading duration considering creep [J]. Journal of Zhejiang University: Engineering Science, 2012, 46(2): 250-256. [15] 刘吉福,郑刚,安关峰.等效时间计算方法研究[J].广西大学学报:自然科学版,2012,37(1): 160-164. LIU Ji-fu, ZHENG Gang, AN Guan-feng. Study on the calculation of equivalent time [J]. Journal of Guangxi University: Nature Science Edition, 2012, 37(1): 160-164. [16] BJERRUM L. Engineering geology of Norwegian normally consolidated marine clay as related to the settlements of buildings [J]. Geotechnique, 1967, 17(2): 83-118. [17] ZHU G F, YIN J H. Elastic visco-plastic finite element consolidation modelling of Berthierville test embankment [J]. International Journal of Numerical and Analytic Methods in Geomechanics, 2000, 24: 491-508. [18] NASH D F T, RYDE S J. Modelling consolidation accelerated by vertical drains in soils subject to creep [J]. Geotechnique, 2001, 51(3): 257-273. [19] HU Y Y, ZHOU W H, CAI Y Q. Large-strain elastic viscoplastic consolidation analysis of very soft clay layers with vertical drains under preloading [J]. Canadian Geotechnical Journal, 2014, 51(2): 114-157. [20] 谢康和.砂井地基:固结理论、数值分析与优化设计[D].杭州:浙江大学, 1987: 22-80. XIE Kang-he. Sand well foundation: consolidation theory, numerical analysis and optimization design [D]. Hangzhou: Zhejiang University, 1987: 22-80. [21] 顾晓鲁,钱鸿缙,刘惠珊,等.地基与基础:第三版[M].北京:中国建筑工业出版社, 2008: 183-198. [22] HU Y Y. A practical evaluation of the surcharge preload period in staged construction subject to creep [J]. Computers and Geotechnics, 2012, 42: 171-179. [23] 刘加才,赵维炳,宰金珉.排水固结下卧层固结度简化计算[J].水运工程,2006, 1: 75-79. LIU Jia-cai, ZHAO Wei-bing, ZAI Jin-min. Simplified consolidation calculation on substratum of ground improved by drainage consolidation [J]. Port and Waterway Engineering, 2006,1: 75-79. 收稿日期:2015-06-16. 基金项目:国家自然科学基金资助项目(51178419). 作者简介:胡亚元(1968—),男,副教授,博士,从事地基处理和土的本构关系研究.ORCID:0000-0002-5422-7679. E-mail:huyayuan@zju.edu.cn DOI:10.3785/j.issn.1008-973X.2016.06.001 中图分类号:TU 47 文献标志码:A 文章编号:1008-973X(2016)06-1009-09 Unified simplified settlement formula based on Yin-Graham’s rheological model HU Ya-yuan, YANG Qiu-hua (ResearchCenterofCoastalandUrbanGeotechnicalEngineering,ZhejiangUniversity,Hangzhou310058,China) Abstract:From the perspective of the idea that under certain condition hypothesis B is approximately equivalent to modified hypothesis A in quasi-plastic visco-elastic model, a new simplified formula of void ratio in terms of equivalent time was proposed based on Yin-Graham’s equivalent time rheological model and using time reduction factor to modify the difference between real time and equivalent time. The formula was valid for any suddenly loading and unloading cases, including loading in normally consolidated soil, loading in over-consolidated soil, unloading and loading after unloading. Two simplified formula of void ratio for the multi-stage construction were established by the means of total consolidation degree method and grading consolidation degree method, respectively. Through comparing with the exact solution and the measured data on site, results show that the calculation error of post-construction settlement by the new simplified formula of void ratio is obviously smaller than those by the classical method and the old equivalent-time method in single-stage construction. The theoretical duration of surcharge preloading and post-construction settlement were analyzed by the total consolidation degree method and the grading consolidation degree method respectively. Both results are approximate to the exact solution. As the total consolidation degree method is much simpler than the grading consolidation degree method, the former is suggested to calculate preloading duration and post-construction settlement in the preloading method. Key words:void ratio; primary and secondary consolidation settlement; simplified formula; calculation error; surcharge preloading