基于Levenberg-Marquardt算法的线性热变形补偿系数矩阵优化

俞慈君, 宋　凯, 李江雄, 金涨军, 樊新田, 章　明

(1. 浙江大学 机械工程学院 浙江省先进制造技术重点研究实验室,浙江 杭州 310027;2.中航工业西安飞机工业(集团)有限责任公司,陕西 西安 710089)



基于Levenberg-Marquardt算法的线性热变形补偿系数矩阵优化

俞慈君1, 宋凯1, 李江雄1, 金涨军1, 樊新田2, 章明1

(1. 浙江大学 机械工程学院 浙江省先进制造技术重点研究实验室,浙江 杭州 310027;2.中航工业西安飞机工业(集团)有限责任公司,陕西 西安 710089)

摘要:根据增强参考系统点(ERS点)热变形的线性特点,建立ERS点线性热变形模型,利用线性热变形补偿系数矩阵对ERS点热变形进行补偿. 提出一种基于Levenberg-Marquardt(LM)算法的线性热变形补偿系数矩阵优化方法,构建多组补偿后的ERS理论值与测量值之间最小加权距离误差函数的优化模型,采用LM算法求解. 以壁板工装为例,通过仿真计算得出在多优化参数、多数据量情况下,优化时间在可以接受的工程应用范围内.通过实验验证了该方法有效地减小了转站误差,修正转站参数,得到的单位温度下的热变形系数矩阵稳定可靠.

关键词：大尺寸测量；转站误差；激光跟踪仪；Levenberg-Marquardt算法；线性热变形

为了提高飞机装配质量,现代飞机装配技术大量使用如激光跟踪仪、iGPS等[1-3]高精度的大尺寸测量设备来提高测量精度.测量设备测量坐标系与装配坐标系的关系通常需要通过测量固定在装配现场的增强参考系统点(points of enhanced reference system, ERS点)进行标定,这个过程称为转站.测量坐标系与装配坐标系的坐标转换参数称作转站参数.求解转站参数通常采用点匹配算法,包括奇异值分解法[4]、正交矩阵法[5]、四组元法[6]、 双四组元法[7]等.Eggert等[8]对前4种算法在工程中的应用进行对比,得出了4种算法精度和稳定性基本相同的结论.

在使用点匹配算法时,由于被测对象的变形和测量误差,测量值与理论值不能完全匹配,造成转站误差.为了减小转站误差,可以从以下方面进行研究.

一方面对匹配算法进行研究.耿娜等[9]和张春富等[10]分别提出了基于刚体运动理论和模式搜索的坐标系匹配算法.后者提出了带工程约束的点匹配算法,把工程约束引入转站算法,并根据不同约束的容差权重对转站误差进行重新分配.Alfons等[12]提出了动态加权的方法,原理是根据测量不确定度对每个测量点分配不同的权重系数来提高转站精度.

另一方面,从仪器测量精度和不确定度方面进行研究.Calkins等[13]提出了基于统一空间测量网络模型的测量点综合不确定度加权评定算法.Mitchell等[14]采用多激光跟踪仪协同工作,以各测量设备的测量协方差矩阵和雅克比矩阵为依据,按照矩阵加权线性最小方差准则来提高坐标转换精度.Predmore[15]建立测量点不确定度椭球误差模型,提出基于参考点马氏距离最小的转站方法.张福民等[16]采用蒙特卡洛仿真方法对大尺寸测量不确定度进行分析.林嘉睿等[17]将激光跟踪仪极高精度测距作为约束,优化跟踪仪测角误差,提高了大空间三维坐标控制网的精度.

布置在工装和地面上的观测点易受温度、碰撞、松动等环境因素影响,导致相对标定时理论值发生偏移,其中温度变化导致的热变形误差最大,超过测量总误差的50%[18].若能对热变形误差进行有效补偿,可以极大提高转站精度.杨宝旒等提出了一种基于三维热变形原理[19]和一种跟踪仪转站热变形误差建模[20]的转站误差补偿方法,两种方法有效地提高了转站精度.三维热变形原理的转站误差补偿方法假设物体在空间3个方向呈现统一的变形情况,仅适用于一般的框式对称布置的ERS点结构;而跟踪仪转站热变形误差建模补偿方法,仿真计算总是在理想条件下,各种实际情况难以准确模拟,适用于装配现场工装数模与实际状态高度一致的情况.

针对ERS点随温度发生的热变形,本研究在线性热变形模型的基础上,利用单位温度下热变形系数矩阵λN×3对观测点热变形补偿,建立多目标匹配函数,提出采用Levenberg-Marquardt(LM)算法进行优化求解的方法,分析测量点组数和待优化参数个数对优化效率的影响.以壁板工装为例,把本文方法与利用转站误差求解出的补偿系数矩阵进行比较.

1转站原理

在飞机数字化装配现场,激光跟踪仪测量布置在现场地面或固定在工装上的ERS点,将实际测量值与理论值匹配运算,获得测量坐标系在装配坐标系下的位置和姿态参数,进而将测量坐标系转换为装配坐标系.图1为转站模型示意图.

图1　转站模型示意图Fig.1　Schematic diagram of orientation model

ERS点是整个装配系统的基准.为了方便地实现转站,保证测量精度,需要在整个测量空间内合理布置ERS点.设转站参数为(α,β,γ,tx,ty,tz),其中(α,β,γ)为测量坐标系在装配坐标系下的姿态参数,用z-y-x欧拉角表示；(tx,ty,tz)为测量坐标系在装配坐标系下的位置参数.平移向量T和旋转矩阵R可以表示为

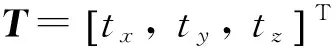
对于不在同一条直线上的N(N>3)个ERS点,第i个ERS点在装配坐标系下的理论值和测量坐标系下的测量值分别设为pAi和pMi.为了求解最佳转站参数,构建N个ERS点关于距离误差的最小二乘函数为

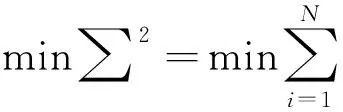
(1)

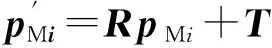
(2)

2ERS点线性热变形模型

(3)

式(3)可简写为

(4)

N个公共观测点热变形系数就构成了系数矩阵λN×3=[λ1, λ2, …, λN]T,单位为mm/℃.

3热变形误差补偿

3.1热变形误差补偿模型

首先利用温度传感器测得现场的实际温度t,计算出与标定温度θ0的温差Δθ.然后假设公共观测点只发生由温度变化引起的线性热变形,由式(4)可以计算出第i个公共观测点在温差Δt下的真实理论值为

(5)

利用跟踪仪测得观测点测量值pMi,则热补偿模型为

(6)

式中：N为公共观测点个数.

3.2补偿系数矩阵直接求解算法

在式(6)中,补偿系数λi表示第i个公共观测点在单位温度下3个方向的热变形量.文献[19]提出了一种通过实验求解单位温度下热变形补偿系数矩阵的方法,本文现只对其简单介绍.

将公共观测点测量值与理论值带入式(1),利用SVD分解法计算出旋转矩阵R和平移矩阵T,再计算出温差Δt,则第i个公共观测点补偿系数λi可表示为

(7)

计算出每个公共观测点的热变形系数可构成单位温度下的热变形系数矩阵λN×3.

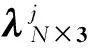
(8)

该方法求出的单位温度下补偿系数矩阵可以减小转站误差,但是存在以下几个方面的不足：

1)转站的目的是为了获得准确的转站参数,该方法几乎没有改变转站参数,只是在转站误差上进行了修正；

2)补偿系数矩阵的计算依赖转站计算方法,随着转站误差变化而变化,不能保证获得稳定的补偿系数；

3)求解方法简单,不能保证获得最佳补偿系数.

4基于LM算法的补偿系数矩阵优化方法

针对上述方法的不足,提出利用LM优化算法计算单位温度下补偿系数矩阵的方法.

4.1Levenberg-Marquardt算法

Levenberg-Marquardt (LM)算法是一种利用标准数值优化技术的优化算法,是梯度下降法与高斯-牛顿法的结合.该方法既具有高斯-牛顿法的局部收敛性,又具有梯度下降法的速度,为大参数化问题提供了快速收敛的正则方法.本文只对其简单介绍,在文献[21]中有关于LM算法的说明.

设E(x)是关于未知参数向量x的目标函数

(9)

式中：e(x)为误差函数.

对于的增量Δx,利用牛顿法则有

Δx=-[2E(x)]-1E(x).

(10)

E(x)=JT(x)e(x),

(11)

2E(x)=JT(x)J(x)+S(x).

(12)

式中：

J(x)为雅可比矩阵,表达式为

(13)

对于高斯-牛顿计算法则有

Δx=[JT(x)J(x)]-1JT(x)e(x).

(14)

LM算法是改进了的高斯-牛顿算法,表示为

Δx=[JT(x)J(x)+μI]-1JT(x)e(x).

(15)

其中,μ为大于0的比例系数,且为常数；I为单位矩阵.从式(15)中可以看出,如果μ取值很大,则LM算法接近梯度下降法,迭代成功一步,μ减小,在接近误差最小值时,逐渐与高斯-牛顿法相似.因此,LM算法精度高,计算速度更快,较原来的梯度下降法速度提高几十倍甚至上百倍,本文利用LM算法进行优化计算.从式(6)中可以看出,待优化参数较多,且优化参数数量随公共观测点数的增加而增加.

4.2构建目标函数

为了提高优化效果与补偿模型的泛化能力,在m个站位,k个温度下测量g组数据.将每组数据带入式(6),那么第n个站位第j个温度下第l组测量数据与修正后的理论值匹配函数为

(16)

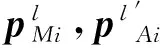
p=(α1,β1,γ1,tx1,ty1,tz1,…,

αm,βm,γm,txm,tym,tzm,λx1,λy1,λz1,…,λxN,λyN,λzN),

总共待优化参数个数P为

P=6×m+N×3.

(17)

4.3选取初始值

(18)

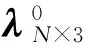
(19)

4.4计算补偿系数矩阵

得到初始值p0后,便可根据LM算法对热变形补偿进行优化计算.数值分析软件Matlab中,优化工具箱提供了解决该优化问题的现成函数Lsqnonlin,该函数可以运用Trust-region-reflective和Levenberg-Marquardt两种算法,默认情况下利用前者求解,所以要使该函数利用LM算法求解,需要利用Options命令设置,μ初值采用默认值0.01.

函数Lsqnonlin优化的函数形式为

min∑2=min (F1(x)2+F2(x)2+…+FS(x)2).

(20)

其中F(x)为目标函数,x为待优化参数.

将式(16)改写成

(21)

4.5分析算法效率

利用LM算法优化求解补偿系数矩阵,需要采集一定量数据带入运算.为了研究算法效率,本文以壁板工装为例,研究采集的数据量Ng和待优化参数个数Np对优化所需时间L的影响.

该壁板工装空间几何结构具有对称性,其上对称布置6个ERS点,布置示意图和理论坐标系如图2所示.

图2　增强参考系统点(ERS点)布局图Fig.2　Points layout of enhanced reference system (ERS)

为了研究测量点组数对优化速度的影响,选择5个站位,每个站位采集60组测量数据,则总共得到300组测量数据.每个站位分别选择18、24、30、36、42、48、54、60组数据,所以总共分别可以得到90、120、150、180、210、240、270、300组测量数据.分别采用第4.1～4.3节中的方法优化计算,得到所需时间如表1所示.为了便于观测优化时间随点组数变化的趋势,以点组数90及其优化时间作为参考,计算其余点组数、优化时间变化率rg、rL,结果如表1所示.图3为点组数变化率和优化时间变化率的趋势.

表1　测量点组数与优化时间变化率

图3　点组数和优化时间变化率Fig.3　Change rates of point groups and optimized time

为了使优化的补偿系数矩阵达到良好的补偿效果,需在不同的站位下采集数据,站位选得越多,补偿模型待优化参数也会越多.为了研究待优化参数个数对优化速度的影响,分别选择5、8、11、14、17、20、23个站位,则待优化总参数分别为48、66、84、102、120、138、156个,每个站位取36组测量数据.分别利用4.1～4.3节中的方法优化计算,得到所需时间如表2所示.同上,以待优化参数个数为48及其优化时间作参考,计算优化参数个数变化率rp和优化时间变化率rL,结果如表2所示.

表2待优化参数个数与优化时间变化率

Tab.2Change rates of optimized parameter numbers and time

序号Npt/srp/%rL/%14810.90026630.737.5%181.7%38467.075.0%514.7%410252.3112.5%379.8%5120104.7150.0%860.6%613899.3187.5%811.0%7156109.5225.0%904.6%

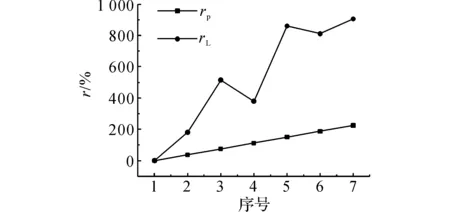
图4　优化参数个数和优化时间变化率Fig.4　Change rates of optimized parameter numbers and optimized time

图4表示待优化参数个数和优化时间变化率趋势图.

从表1、2数据结果和图3、4可以看出：1)随着测量点组数增加,优化所需时间变化率相对点组数变化率较慢,在点组数变化率为233.3%时,优化时间变化率为88.3%,所需时间为13.7 s；2)随着待优化参数增加,点组数同时增加,优化所需时间有增加趋势,优化时间变化率比优化参数个数变化率快,当待优化参数变化率为225.0%时,优化所需时间变化率为904.6%,但所需优化时间为109.5 s.LM算法也是迭代计算,由于站位的选择、测量数据、初值等原因,在优化102和138个待优化参数时,优化过程提前收敛,时间减少,属于正常波动.

综上,可以看出该方法在多优化参数、多数据量情况下能保证计算效率,优化时间在工程应用中属于可以接受的范围内.

5对比实验

5.1实验方法

为了验证本文方法的有效性,以图2所示的壁板工装为例,分别用前述2种方法计算补偿系数矩阵,比较转站误差、转站参数相对未补偿转站参数的变化,研究ERS点个数变化情况下补偿系数矩阵的变化.

实验平台主要由飞机壁板工装、型号为AT901的徕卡激光跟踪仪及其配套设备(包括主机、气象站等)、温度传感器(精度为±0.1 ℃)、电脑(装有测量软件)等组成,如图5所示.

图5　转站温度补偿实验平台Fig.5　Experiment platform for temperature compesa-tion in orientation

在7.2 ℃条件下标定出各个点的理论坐标值pAi,采集不同温度下ERS点在跟踪仪坐标系下的测量值.由于车间温度变化缓慢,可以假定数据采集期间车间温度恒定,且壁板工装充分热变形,与周围环境不发生热交换.通过温度传感器测得实际温度分别为8.5,10.3,13.6,16.4,20.5,22.4和25.7 ℃,在每个温度下采集20组测量数据,得到数据集A.

5.2线性模型分析

补偿系数矩阵能够对公共观测点实现有效的补偿,其假设条件是热变形模型为线性模型,所以本文先对公共观测点随温度的变化进行分析.利用集合A中的数据,计算各温度下每组数据在x、y、z3个方向上的转站误差,得到20组转站误差数据.为了减小测量误差对转站误差的影响,取20组转站误差数据平均值作为该温度下的转站误差.由于ERS点对称布置,为表达方便,将工装一侧的ERS1、ERS3、ERS5在各个方向上的平均转站误差error列出,如表4所示.

为了发现变形规律,绘制出表中数据随温度变化的关系图,如图6所示.从图6可以得出：1)不同观测点各个方向上随温度变化情况不同；2)公共观测点在x、y方向上呈线性关系,且温差越大,线性关系越显著.由于工装在z方向上尺寸较小,热变形量也较小,与测量误差相比不可忽略,使得在该方向上线性关系不显著.

图6　ERS(1、3、5)点转站误差随温度变化图Fig.6　Relationship between orientation error of ERS(1、3、5)and temperatures

mm

5.3转站误差与转站参数变化比较

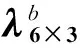
采用转站误差平均值作为转站精度的评价指标,计算公式如下：

(22)

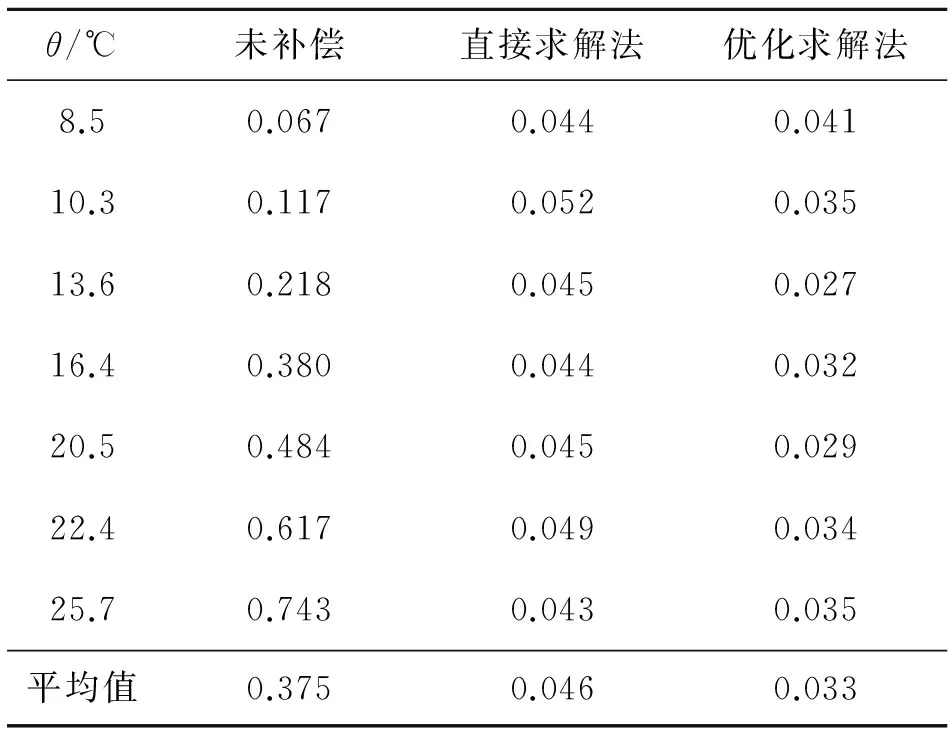
表5　各个温度下转站平均误差

如图7所示为2种求解方法的转站平均误差随温差的变化关系.

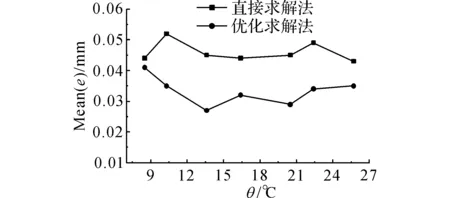
图7　平均转站误差和温度的关系Fig.7　Relationship between mean orientation error and temperature

比较直接求解法、优化求解算法计算得到转站参数与未补偿转站参数差值Δα、Δβ、Δγ、Δtx、Δty、Δtz,如表6所示.

表6直接求解法与优化求解法转站参数修正量对比表

Tab.6Comparison of conversation station parameter correction between direct solution method and optimal solution method

θ/℃ 直接求解法 优化求解法 Δα/(×10-5rad)Δβ/(×10-5rad)Δγ/(×10-5rad)Δtx/mmΔty/mmΔtz/mmΔα/(×10-5rad)Δβ/(×10-5rad)Δγ/(×10-5rad)Δtx/mmΔty/mmΔtz/mm8.50.110-0.0440.001-0.0003-0.00030.00012.4388.6791.434-0.0270.0040.00710.30.254-0.106-0.016-0.0070-0.00080.00043.3181.8671.713-0.0650.0090.00213.63.761-0.0973.228-0.0001-0.00010.0001-39.1654.253-44.720-0.0370.0170.00316.45.465-0.1424.699-0.0002-0.00020.00026.2886.112-64.273-0.0550.0250.00420.50.807-0.437-0.332-0.0003-0.00030.000236.05274.45025.763-0.0800.0400.00522.41.276-0.509-0.006-0.0003-0.00040.000228.48410.1451.675-0.1220.0410.00825.70.110-0.0440.001-0.0004-0.00040.00032.4388.6791.434-0.1920.0500.010

5.4补偿系数矩阵随ERS点个数变化的比较

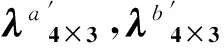
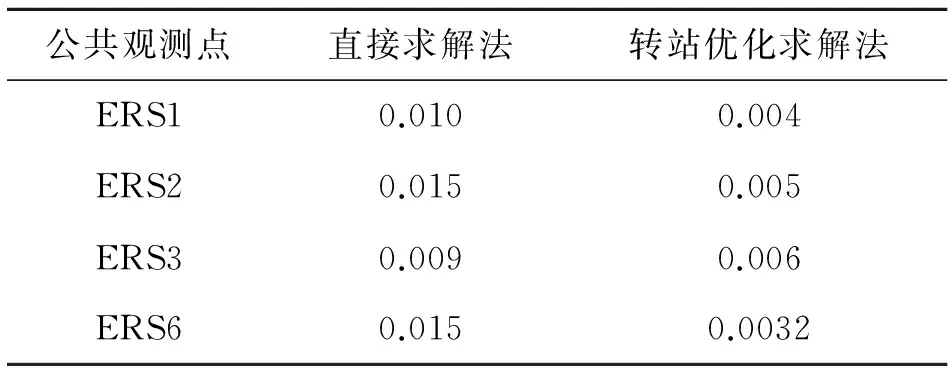
表7　补偿系数矩阵变化表

图8　补偿系数矩阵变化图Fig.8　Change chart of compensation coefficient matrix

5.5数据分析与结论

(1)由表5、图7知,随着温差的增大,转站误差也随之增大,两种方法能够有效减小转站误差：转站误差补偿法减小了87.8%,优化求解方法减小了91.1%.因此,通过转站误差补偿法求得补偿系数矩阵不是最优值,存在可优化空间.

(2)根据表6可以看出,利用直接求解法计算得到的平移参数变化范围为-0.000 8～0.000 4 mm,变化较小,表明了该方法的局限性；优化求解算法计算得到平移参数变化范围为-0.192～0.050 mm,变化较大,且随温差的增大,平移参数变化越明显,表明该方法对转站参数进行了修正.

(3)从表7、8可以看出,ERS点个数变化时,优化求解算法计算得到的单位温度下补偿系数比直接求解法稳定,证明了本文方法的优越性.

5结语

通过对转站原理分析,针对均匀稳定温度场下的线性热变形模型,利用单位温度下补偿系数矩阵对公共观测点理论值进行补偿,并提出基于LM算法的补偿系数矩阵优化方法.

(1)随着测量点组数、待优化参数的增加,该算法仍能保持优越的计算速度；

(2)利用该算法优化求解出的单位温度下补偿系数矩阵进行补偿后,有效的减小了转站误差,修正了转站参数；

(3)ERS点变化时,采用优化求解算法计算得到的单位温度下补偿系数矩阵更稳定.

参考文献(References)：

[1] 杜福洲,陈哲涵,唐晓青.iGPS测量场精度分析及其应用研究[J].航空学报, 2012, 33(9): 1737-1745.

DU Fu-zhou, CHEN Zhe-han, TANG Xiao-qing. Precision analysis of iGPS measurement field and its application [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1737- 1745.

[2] 曲巍崴,董辉跃,柯映林.机器人辅助飞机装配制孔中位姿精度补偿技术[J].航空学报,2011, 32(10): 1951-1960.

QU Wei-wei, DONG Hui-yue, KE Ying-lin. Pose accuracy compensation technology in robot-aided aircraft assembly drilling process [J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1951-1960.

[3] 郭洪杰,王碧玲,赵建国.iGPS测量系统实现关键技术及应用[J].航空制造技术, 2013 (11)： 46-49.

GUO Hong-jie, WANG Bi-ling, ZHAO Jian-guo. Key technology and application of iGPS measuring system [J]. Aeronautical Manufacturing Technology, 2013(11)： 46-49

[4] ARUN K S, HUANG T S, BLOSTEIN S D. Least-squares fitting of two 3-D point sets [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1987(5): 698 - 700.

[5] HORN B K P. Closed-form solution of absolute orientation using unit quaternions [J]. Journal of the Optical Society of America A, 1987, 4(4): 629-642.

[6] HORN B K P, HILDEN H M, NEGAHDARIPOUR S. Closed-form solution of absolute orientation using orthonormal matrices [J]. Journal of the Optical Society of America A, 1988, 5(7): 1127-1135.

[7] WALKER M W, SHAO L, VOLZ R A. Estimating 3-D location parameters using dual number quaternions [J]. Cvgip Image Understanding, 1991, 54(91): 358-367.

[8] EGGERT D W, LORUSSO A, FISHER R B. Estimating 3-D rigid body transformations: a comparison of four major algorithms[J]. Machine Vision and Applications, 1997, 9(5/6): 272-290.

[9] 耿娜,邾继贵,劳达宝,等.基于刚体运动学的坐标系配准理论及算法[J].传感技术学报, 2010, 23(8): 1088-1092.

GENG Na, ZHU Ji-gui, LAO Da-bao, et al. Theory and algorithm of co-ordinate system registration based on rigid body kinematics [J]. Chinese Journal of Sensors and Actuators, 2010, 23(8): 1088-1092.

[10] 张春富,张军,唐文彦,等.一种基于模式搜索的大尺寸测量移站坐标转换方法[J]. 计测技术, 2003, 23(6): 12-14. ZHANG Chun-fu, ZHANG Jun, TANG Wen-yan, et al. A coordinate transformation method of moving the station of large scale measurement based on mode searching[J]. Aviation Metrology and Measurement Technology, 2003, 23 (6): 12-14.

[11] 俞慈君,李江雄,余锋杰,等.带工程约束的点匹配算法[J].机械工程学报, 2010, 46(5): 183-190.

YUN Ci-jun, LI Jiang-xiong, YU Feng-jie, et al. 3D points registration algorithm with engineering constraints [J]. Journal of Mechanical Engineering, 2010, 46(5): 183-190.

[12] ALFONS M, SCOTT S. Dynamic weighting of laser tracker measurements for bundle adjustment [R]. Leica Geosystems， 2014.

[13] CALKINS J M, SALERNO R J. A practical method for evaluating measurement system uncertainty [C]∥ Boeing Large Scale Metrology Conference. Long Beach: [s. n.], 2000.

[14] MITCHELL J P, SPENCE A D, HOANG M, et al. Sensor fusion of laser trackers for use in large-scale precision metrology[J]. Intelligent Manufacturing, 2004: 57-65.

[15] PREDMORE C R. Bundle adjustment of multi-position measurements using the Mahalanobis distance [J]. Precision Engineering, 2010, 34(1): 113-123.

[16] 张福民,曲兴华,叶声华.基于蒙特卡罗仿真方法的大尺寸测量不确定度分析[J].计算机集成制造系统, 2009, 15(1): 184-188.

ZHANG Fu-min, QU Xing-hua, YE Sheng-hua. Uncertainty analysis in large-scale measurement based on Monte Carlo simulation method [J]. Computer Integrated Manufacturing Systems, 2009, 15(1): 184-188.

[17] 林嘉睿,邾继贵,郭寅,等.现场大空间测量中精密三维坐标控制网的建立[J].机械工程学报, 2012, 48(4): 6-11.

LIN Jia-rui, ZHU Ji-gui, GUO Yan, et al. Establishment of precise three-dimensional coordinate control network in field large-space measurement [J]. Journal of Mechanical Engineering, 2012, 48(4): 6-11.

[18] 费业泰.机械温度变形理论及应用[M].北京: 国防工业出版社, 2009: 1-13.

[19] 俞慈君,杨宝旒,金涨军,等.基于三维热变形原理的转站误差补偿方法[J].浙江大学学报: 工学版, 2015,49(7): 1208-1214.

YU Ci-jun, YANG Bao-liu, JIN Zhang-jun, et al. A compensation method for registration error of laser tracker based on 3-D anisotropic thermal-deformation theory [J]. Journal of Zhejiang University: Engineer Science), 2015, 49(7): 1208-1214.

[20] 杨宝旒,俞慈君,金涨军,等.激光跟踪仪转站热变形误差建模与补偿方法[J].航空学报, 2015, 36(9):3155-3164.

YANG Bao-liu, YU Ci-jun, JIN Zhang-jun, et al. Thermal deformation error modeling and compensation approach for laser tracker orientation [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9):3155-3164.

[21] HAGAN M T, MENHAJ M B. Training feedforward networks with the Marquardt algorithm [J]. IEEE Transactions on Neural Networks, 1994, 5(6): 989-993.

收稿日期：2015-07-12.

基金项目：国家自然科学基金资助项目(51505422);国家自然科学基金创新研究群体科学基金项目(51521064);中央高校基本科研业务费专项资金资助项目(2015FZA4002).

作者简介：俞慈君(1981—)，男，副研究员，从事飞机数字化装配测量技术研究. ORCID：0000-0001-9380-9009. E-mail：Yuppy@zju.edu.cn 通信联系人：章明，男，工程师.ORCID：0000-0003-3529-4259. E-mail：zhgmg@126.com

DOI:10.3785/j.issn.1008-973X.2016.06.007

中图分类号：V 262.4

文献标志码：A

文章编号：1008-973X(2016)06-1056-09

Optimization of linear thermal deformation compensation coefficient matrix based on Levenberg-Marquardt algorithm

YU Ci-jun1, SONG Kai1, LI Jiang-xiong1, JIN Zhang-jun1, FAN Xin-tian2, ZHANG Ming1

(1.KeyLaboratoryofAdvancedManufacturingTechnologyofZhejiangProvince,CollegeofMechanicalEngineering,ZhejiangUniversity,Hangzhou310027,China; 2.AviationIndustryCorporationofChinaXi’anAircraftIndustry(Group)Co.Ltd,Xi’an710089,China)

Abstract:According to the linear feature of enhanced reference system (ERS) point thermal deformation the linear thermal deformation model of ERS points was established, and the thermal deformation of ERS points was compensated by linear thermal deformation compensation coefficient matrix. A linear thermal deformation compensation coefficient matrix optimization method based on Levenberg-Marquardt (LM) algorithm was presented. An optimization model of the minimum weighted distance error function between the ERS theoretical value compensated and the actual measurement value was constructed. A panel fixture was studied as an example and the simulation showed that the optimization time is within the acceptable engineering application in the case of multi parameters and data. Finally, the experimental results verify that the proposed method can effectively reduce the registration error and correct the registration parameters, and the thermal deformation coefficient matrix is stable and reliable.

Key words:large size measurement; registration error; laser tracker; Levenberg-Marquardt algorithm; linear thermal deformation