基于FastICA算法的物理漏损流量分析模型

郑成志, 高金良, 何文杰,2

(1.哈尔滨工业大学 市政环境工程学院,黑龙江 哈尔滨 150090； 2.天津市自来水集团有限公司,天津 300040)



基于FastICA算法的物理漏损流量分析模型

郑成志1, 高金良1, 何文杰1,2

(1.哈尔滨工业大学 市政环境工程学院,黑龙江 哈尔滨 150090； 2.天津市自来水集团有限公司,天津 300040)

摘要:为解决传统供水管网物理漏损流量分析模型模拟准确度不高、无法体现物理漏损流量与水头关系的不确定性等问题,基于快速独立成分分析(FastICA)算法构建物理漏损流量分析模型. 该模型将供水总流量划分为用水流量和物理漏损流量,并视为2个源信号.以供水总流量和管网入口处水头2个参数为输入参数,通过源信号分离获得2个流量的波形信息,通过比较相关系数确定源信号的顺序,通过水平衡方程确定物理漏损流量的真实尺度,实现物理漏损流量在时间序列上的模拟. 该模型输入参数易于获取且有效避免了物理漏损流量与水头关系的复杂性,在单水源供水管网中模拟准确度较高,并且在供水管网水力模型节点流量分配中得到了较好的应用.

关键词：供水管网；物理漏损；快速独立成分分析(FastICA)算法

供水管网漏损造成巨大的水资源和能量浪费,物理漏损是供水管网漏损的主要组成部分[1]. 建立供水管网物理漏损流量分析模型,从而解决漏损量难以估计的问题,将有助于漏损控制与调度、供水安全预警等工作.

在单个漏点物理漏损流量模拟方面,比较典型的模型有孔口出流模型[2]、FAVAD模型[3-4]、指数模型[5-6]、压力驱动节点流量模型[7-8]、漏损沿管线分配模型[9]等. 在指数模型中,物理漏损流量为漏损系数与供水管道内部水头的漏损指数次方的乘积,其表达式最为简单,对物理漏损流量与水头的关系拟合度也很高,得到最为广泛的工程应用. 漏损系数和漏损指数受管道材质、漏损水力条件、土壤水力条件、漏点大小、漏点形状等因素影响很大[10-11],这些影响因素由于管道敷设于地下很难全面获知,造成物理漏损流量很难明确. 此外,理论上漏损指数的取值范围为0.5～2.5[12],取值区间很大,因而导致单个漏点物理漏损流量与水头的关系具有复杂性.

在供水管网物理漏损流量模拟方面,传统模型主要将供水管网物理漏损流量视为管网中所有漏点的物理漏损流量之和. 这些模型以单个漏点的指数模型为基础,其中最能反映真实状况的为理想模型[13](模型假定每个漏点的漏损系数和漏损指数已知),但是尚无法应用. 在实用的模型中,按照不同方法处理漏损系数和漏损指数,根据模型接近理想模型的程度,现阶段主要发展了等效漏点指数模型[14]、一致漏损模型[15]、夜间最小流量模型(漏损系数分类取值模型)[16-17]、漏损系数比例取值模型[18]和BABE模型[19]. 这些供水管网物理漏损流量分析模型不同程度地存在参数取值主观性强、模型校核缺乏可靠数据的问题,使得这些模型对于供水管网物理漏损流量的模拟并不准确.

近期研究发现,单个漏点物理漏损流量与水头关系具有不确定性(由于管材存在黏弹性,使得相同水头下升压过程比降压过程物理漏损流量要小)[20],而以往所有供水管网物理漏损流量分析模型均是以水头为自变量,按照漏损流量与水头的单调关系式建立的,无法模拟出这种不确定性.

为有效解决或者避免物理漏损流量与水头关系复杂性问题,反映出物理漏损流量与水头关系的不确定性,本文通过FsatICA算法构建模拟准确的供水管网物理漏损流量分析模型.

1FastICA算法概述

快速独立成分分析算法,简称FastICA算法,是1997年由芬兰阿尔托理工大学提出并发展起来的.该算法基于非高斯性最大化原理,采用牛顿迭代算法对混合信号进行批处理,从混合信号中分离出各个源信号[21]. FastICA算法是ICA算法中的一种,主要解决盲源分离问题,在不知道源信号本身和源信号如何混合的情况下,假设源信号之间相互统计独立.该算法的基本原理如图1所示.

图1　FastICA的原理框图Fig.1　Structure of FastICA principle

FastICA算法较其他算法收敛速度快(至少是二次方的),不用选择步长参数,不需要对源信号的概率密度函数进行估计,非线性函数的选择具有任意性,继承了神经网络算法的许多优点,在矿产勘查、遥感图像分类、图像降噪、数据通信与阵列信号处理、生物医学信号处理、文本分析与数据挖掘、计量经济学等诸多领域得到了较好的应用[21-23]. 原理上,FastICA算法的应用尚需要满足以下条件：源信号之间相互统计独立；源信号数目不大于观测信号数目；源信号中至多有1个满足高斯分布.另外,FastICA算法分离出的源信号具有不确定性：源信号排列顺序的不确定性和源信号尺度的不确定性.

2FastICA算法分离物理漏损流量的适用性

2.1供水管网物理漏损流量的划分

按照IWA提供的水平衡分析方法,在体积上供水总量由4部分组成：售水量、免费供水量、账面漏水量和物理漏水量[24].由于并不是所有的出水点都被实时计量流量,而且物理漏损流量同其他流量一起混合在供水总流量中,很难明确供水管网中任一时刻的物理漏损流量.

由于供水管网节点流量包括用户实际用水量和物理漏损水量[25],研究将供水总流量QZ划分为两部分：物理漏损流量QL和用水流量QY,其中物理漏损流量对应物理漏水量,用水流量对应售水量、免费供水量和账面漏水量,并得到基本关系式：

QZ=QY+QL.

(1)

2.2FastICA算法的适用性分析

将供水管网中物理漏损流量和用水流量视作2个源信号,将供水总流量和管网入口附近水头视作2个观测信号,在源信号变化时如何通过一定内在规律反映到观测信号上的变化还不清晰时,可以考虑从观测信号分离出源信号,这个问题可以用FastICA算法解决.

2.2.1源信号之间的独立性物理漏损流量随漏点处水头改变而改变,用水流量的变化又会引起供水管网的水头发生变化,因此用水流量的改变会引起物理漏损流量的变化.严格说来，供水管网中物理漏损流量和用水流量之间并不独立,两者具有相关性，但是供水运营调度工作总是设法降低用水流量变化对供水管网水头的影响程度,从而维持用户最基本的用水水头需求.因此，用水流量对物理漏损流量影响比较小,两者相关性比较小. 另外,有研究证明FastICA算法用于处理一些源信号.具有弱相关性的问题，分离效果也能满足工程应用[26-27].综上所述,应用FastICA算法可以尝试在供水管网系统分离物理漏损流量.

2.2.2信号数目的完备问题研究将供水总流量和管网入口附近水头2个参数作为观测信号,使得源信号数目等于观测信号数目,观测信号数目是完备的.

2.2.3源信号的高斯性供水管网中对用户水量的计量仪器绝大部分是水表,只能得到一段时期内的用水体积,而无法得知每一时刻用水流量.因此，即使供水总流量实现了流量计计量,按照式(1)也无法获知每一时刻物理漏损流量,而通过停止所有用户用水进行实验测量的条件难以达到,导致供水管网物理漏损流量具有不可测性.

供水管网物理漏损流量的不可测性使得任意供水管网鲜有物理漏损流量数据.通过水力学基本知识,构建物理漏损流量概率密度函数也很困难.通过样本数据和概率密度函数研究物理漏损流量统计分布特征的方法均不可行.用水流量统计分布的研究也面临同样问题.

供水管网运行中供水总流量的数据基本被测量并保留下来,本文研究供水总流量的统计分布特征,从而推断物理漏损流量和用水流量的大致统计分布特征.用下式计算峰度系数衡量随机变量的非高斯性程度：

(2)

式中：t为数据随时间的信号，t=1,2,…,T，x为随机变量.

选取我国2个供水管网计量分区的每时刻t实测数据进行分析,其中1个是北方城镇TJ市,1个为南方城镇CP镇,实测2个计量分区供水总流量变化如图2所示.

图2　随时间变化的供水总流量Fig.2　Total water supply flow in time series

对实测2个计量分区供水总流量(QZ)进行统计分布特性分析(见表1)，其中，QZmin、QZmax、QZave分别为供水总流量的最小值、最大值、平均值，kurt(QZ)为峰度系数，N为实验采集的数据个数，由表1可知峰度系数均远小于3,供水总流量为亚高斯分布,并且具备很强的非高斯性.

表1　供水总流量统计分布特性分析

上述2个典型计量分区供水总流量是非高斯的,但是这一结论尚不能推广至所有供水管网计量分区,不失一般性,假定某一计量分区供水总流量是非高斯信号,作如下推导：

已知：某计量分区供水总流量是非高斯信号；

推导：假设该计量分区用水流量和物理漏损流量均是高斯信号,按照数学原理：高斯信号的线性组合仍然是高斯信号,由式(1)可得，该计量分区供水总流量是高斯信号,这与已知条件矛盾,故假设不成立；

结论：某计量分区供水总流量是非高斯信号,则该计量分区用水流量和物理漏损流量至多有1个高斯信号.

综合以上分析论证,只要供水总流量具备非高斯性,则FastICA算法可以实现从供水总流量中分离出物理漏损流量的工程应用.

3物理漏损流量分析模型的构建

3.1源信号的分离

使用FastICA算法构建供水管网物理漏损流量分析模型,混合模型如下式：

(3)

式中：X为观测信号矩阵；A为混合矩阵；S为源信号矩阵；x1(t)为观测信号矩阵中第一行数据,即供水总流量QZ；x2(t)为观测信号矩阵中第二行数据,供水管网入口附近水头Hen；a11、a12、a21、a22均为混合矩阵中的元素,混合矩阵为2×2矩阵；s1(t)为源信号矩阵中第一行数据,即用水流量；s2(t)为源信号矩阵中第二行数据,即物理漏损流量.

对观测信号做白色处理,如下式：

(4)

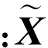
解混模型如下式：

(5)

(6)

构建非平方的非线性函数如下式：

(7)

式中：G(·)为非平方的非线性函数.

建立负熵的近似表达式,即对比函数如下式：

(8)

构建目标函数如下式：

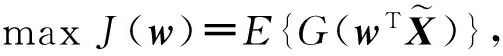
(9)

式(9)使用牛顿迭代法求解,迭代公式如下式：

(10)

可行性约束函数如下式：

(11)

式中：ξ为阈值.

FastICA算法每次只分离出1个源信号,在分离其他源信号时,为了防止分离出的源信号重复,使用正交化投影操作对不同的w作去相关处理. 经过源信号的分离,得到各个源信号的波形信息.

3.2源信号顺序的确定

利用斯皮尔曼方法求解相关系数,表达式如下式：

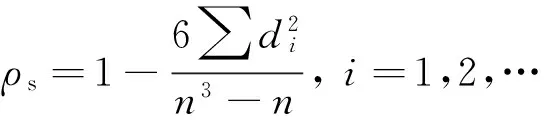
(12)

式中：ρs为相关系数，di为成对变量的等差级数,n为等级个数.

杨琳的老伴退休后，在生活区路边树下搭建了一间小修理店，专修单车。欧阳橘红找到小修理店。杨琳的老伴是钳工，她对这个老钳工印象有些模糊了，老钳工一眼就认出了她。杨琳比老钳工小十岁，杨琳和老钳工生了两男一女。大儿子因偷盗坐了牢，二儿子和小女儿下岗了。这些都是她来滨湖后才知道的。

斯皮尔曼相关系数取值介于-1.0～1.0,相关系数越大,表明2个信号之间的变化趋势越接近. 有理由认为漏损水平较低的供水管网中,供水总流量的变化趋势主要是由用水流量决定的,而供水水头通常与供水总流量出现相反的变化趋势,因此用水流量与供水总流量的相关系数一般要大于物理漏损流量与供水总流量的相关系数.分别计算2个源信号与供水总流量的相关系数,较大的那个认定为用水流量；或者分别计算2个源信号与管网入口附近水头的相关系数,较大的那个认定为物理漏损流量.

3.3源信号尺度的确定

基于FastICA算法构建的物理漏损流量分析模型得到的物理漏损流量信号和用水流量信号仅具有波形信息,为确定源信号尺度,具体过程如下.

首先,假设分离得到源信号的波形信息与真实值的波形信息一致,即得到下式：

y1(t)∝QY(t)，y2(t)∝QL(t).

(13)

式中：y1(t)为分离得到的用水流量信号,无量纲；QY(t)为真实用水流量；y2(t)为分离得到的物理漏损流量信号,无量纲；QL(t)为真实物理漏损流量.

对分离得到的用水流量信号和物理漏损流量信号按下式处理：

(14)

由于使用FastICA算法分离得到的信号方差均为1,此时y10(t)和y20(t)都是均值为0、方差为1的数据序列,此时下式成立:

(15)

式中：σY为实际用水流量序列的标准差，σL为实际物理漏损流量序列的标准差，μY为实际用水流量序列的均值，μL为实际物理漏损流量序列的均值.

此时,若将σY、σL、μY、μL这4个参数看做未知数,由流量平衡关系可列方程组如下式：

(16)

式中：QZ(t)为实际供水总流量.

又有下式成立：

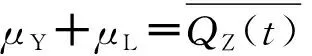
(17)

将式(17)代入式(16),得下式：

(18)

如式(18)为二元一次超定方程组,系数矩阵列满秩,存在唯一的最小二乘解,可求得参数σY、σL的值；另外,通过水平衡分析报告或者夜间最小流量法可知μY、μL这2个参数的值. 将σY、σL、μY、μL这4个参数代入式(15)即可确定2个源信号的尺度.

3.4模型的求解

在对用水流量和物理漏损流量2个源信号进行分离时,以供水总流量和管网入口处水头为输入参数,使用Matlab软件中FastICA工具箱求解.通过编写Matlab求解程序确定源信号顺序和尺度,其中参数σY、σL的求解使用遗传算法.

4物理漏损流量分析模型的验证

基于FastICA算法的供水管网物理漏损流量分析模型中没有供水管网的属性参数,也没有可供优化取值的可变参数,因此该模型无须校核.实际供水管网中几乎无法单独获得用水流量或者物理漏损流量数据,除非所有用户是使用流量计计量的,且其计量数据被实时采集与保存.这导致所建模型在实际供水管网中难以验证,本研究通过实验室供水管网来验证模型.

4.1供水管网漏损实验简介

实验室供水管网如图3所示.该供水管网由12个基环构成,共有18个出水点,每个出水点安装1个水表计量水的体积；水泵出口安装稳压罐,能够实现压力较为稳定的工况. 管道流量由流量计计量、压力由压力表计量、用水流量在水表上安装流量记录器通过体积法计算.

开展供水管网物理漏损实验时,固定部分出水点阀门开度不变,视为漏点. 其他出水点视为用水点,通过这些出水点阀门开度的调节及水泵运行频率的调节形成不同的用水工况. 实验时采用单水源供水形式,传感信号存储频率为1 Hz.

图3　供水管网漏损实验室Fig.3　Leakage test laboratory of water distribution network

4.2观测数据分析

实验共计时间8 389 s,删掉不稳定状态(主要是工况切换形成瞬态所致)时间内数据,剩余有效时间长度7 362 s,形成连续的24个稳定工况(工况编号为N),如图4所示.经过计算,供水总流量的峰度系数为2.49,为亚高斯信号,具备非高斯性,符合模型的应用条件.

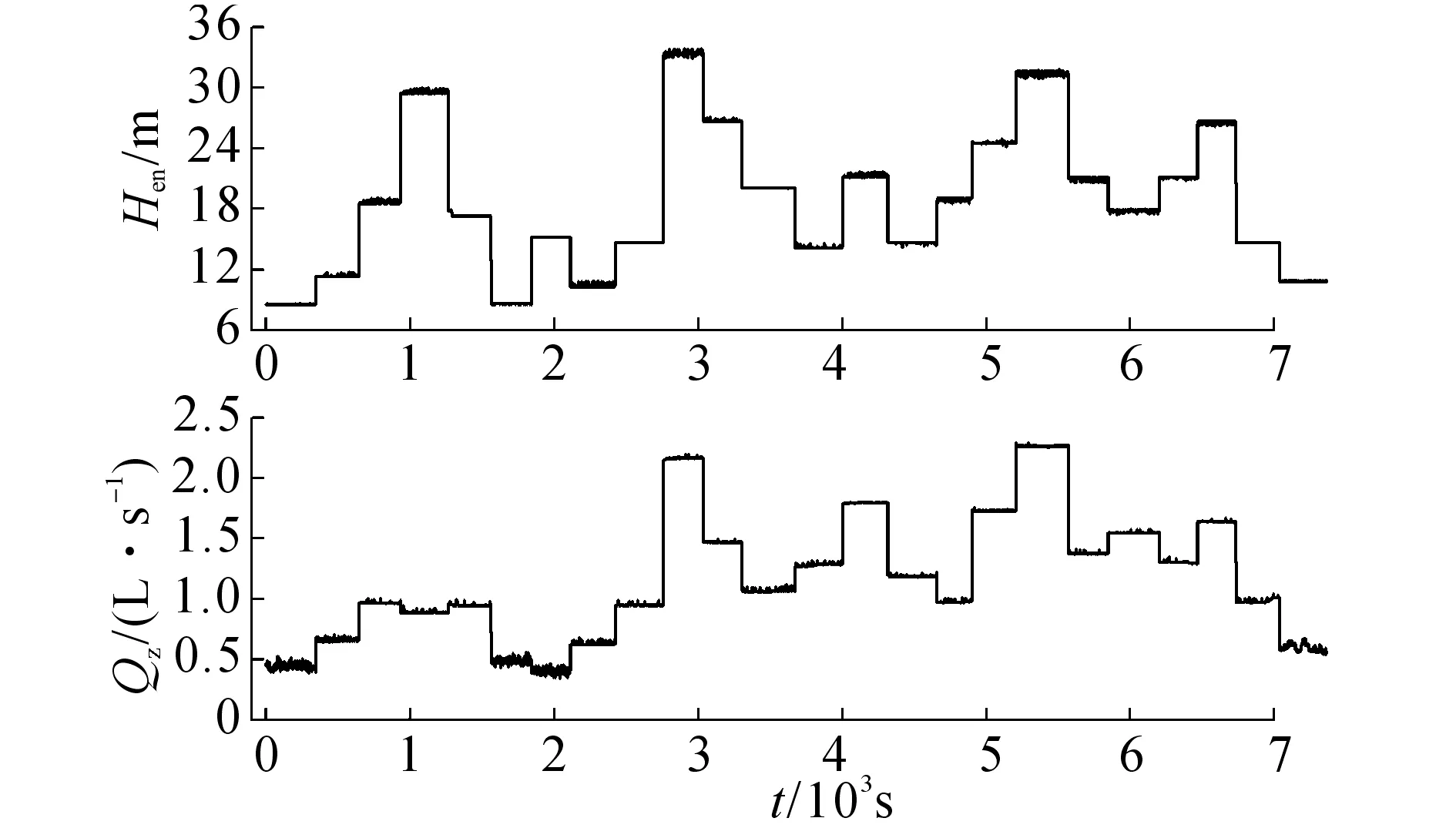
图4　实测供水总流量和水头Fig.4　Measured total water supply flow and pressure head

4.3模拟效果分析

使用模型模拟得到2个源信号的波形信息如图5所示.经过计算,第一个源信号与供水总流量的相关系数为0.958 8,第二个源信号与供水总流量的相关系数为0.327 6,可以判断第一个源信号对应供水总流量的变化趋势、第二个源信号对应物理漏损流量的变化趋势.

经过水平衡方程求解,确定源信号的真实尺度,各工况取均值得物理漏损流量模拟结果及相对误差δ如图6所示.由图6可知,在24个工况中,物理漏损流量最大模拟误差达到15.0%左右. 经计算,物理漏损流量模拟误差绝对值平均值为5.68%,可见模型对供水管网物理漏损流量的模拟是较为准确的.

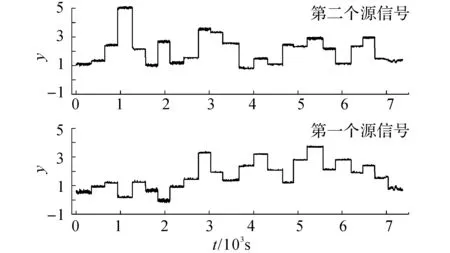
图5　源信号的模拟结果Fig.5　Simulation results of source signals

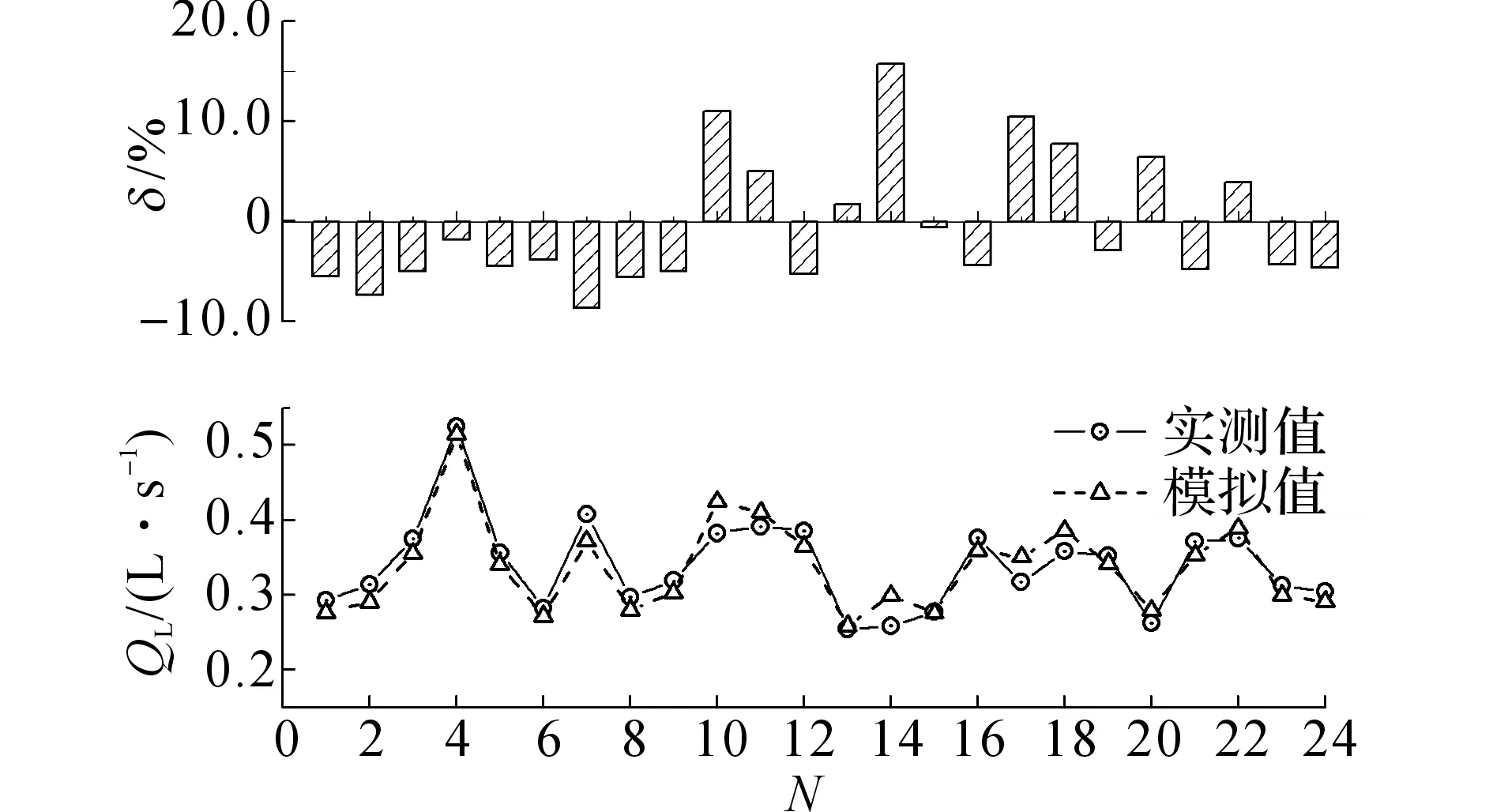
图6　物理漏损流量模拟结果和误差分析Fig.6　Simulation results and error analysis of leakage discharge

5物理漏损流量分析模型性能分析

通过上述分析,基于FastICA算法的物理漏损流量分析模型有以下主要特点：

1)模型输入参数为供水总流量、管网入口附近水头和物理漏损率(可通过物理漏损体积评估法得出,例如自上而下水平衡分析法[14]),模型输出为各工况下的物理漏损流量,模型输入参数少、易于获取；

2)模型将整个供水管网的物理漏损流量视为1个整体,所建模型不包含供水管网任何属性,有效回避了物理漏损流量与水头关系的复杂性；

3)供水管网物理漏损流量的变化势必反映在供水总流量中,模型输入参数变化导致模型输出变化,即使供水水头一样,也可得到不同的物理漏损流量,模型可以体现漏损流量与水头关系的不确定性；

4)在单水源供水管网中,模型对于供水管网物理漏损流量的模拟准确度较高.

6物理漏损流量分析模型的应用

某市供水管网水力模型构建过程中,流量Q中,节点流量采用自上而下的分配方法,具体如下式：

(19)

式中：Qnet为除大用户外需被分配的流量；QD为大用户的流量；Qrem为差值流量；QV为用户按照月用水体积和用水模式换算的流量；Vm为用户月用水体积；Cp为代表用户用水规律的用水模式,并且用水系数为ξ；QN为按地址被准确分配的流量,并且

QN=∑QD+∑QV.

使用上述方法及测得的各类用户用水变化规律,对该市供水管网进行节点流量分配,期间发现某些计量区域内某些时刻的差值流量为负数.该项目中差值流量出现负数的原因可能是很多的,比如分区流量计计量误差、大用户计量误差、用户月用水体积计量误差和用户用水规律误差.这在所有水力模型中会面临同样的误差问题,造成差值流量不准确. 另外,该市计量水量占比很高,差值流量的主要部分可以视为物理漏损流量,项目实施中发现差值流量与水头的关系背离实际规律.

图7　原始节点流量分配状况Fig.7　Previous status of node demand distribution

项目组成员认为造成差值流量异常的主要原因是用户用水规律误差. 为说明用户用水规律误差对差值流量的影响,本文将问题简化,用居民类用水规律代替所有用户用水规律,某计量区域内的产销差按照10%处理,出现的问题如图7所示.由图7可知,使用原始的用水规律进行节点流量分配时,由于用水规律的误差,使得部分时刻分配的流量大于流量计计量的供水总流量,导致算出的差值流量为负数. 另外,因为计量水量体积占供水总体积的90%,差值流量主要反映了物理漏损流量的大小,预期差值流量应该随着水头的变大而增加,但是没有实现预期.

用水规律的误差是由个体用户的用水规律代替整体同类用户用水规律的必然结果,表现在用水系数在时间上的分配错误,例如出现差值流量为负数时,用水系数过大. 在缺少差值流量序列的情况下,现阶段缺乏有效方法修正用水规律.

本研究通过所建模型求解各时刻物理漏损流量(该例中物理漏损按照产销差的70%处理),对差值流量与物理漏损流量之差进行非负约束,从而修正用户用水规律,节点流量仍然是自上而下的分配方法,具体实施方式由式(19)发展为式(20)：

(20)

该实例中,观测信号数据如图8所示.

经过FastICA算法模拟得到2个源信号如图9所示.经过计算,第一个源信号与供水总流量的相关系数为-0.961 7,第一个源信号与供水水头的相关系数为0.889 8,可以判定第一个源信号为物理漏损流量、第二个源信号为用水流量. 另外,第二个源信号与供水总流量的相关系数为0.999 1,第二个源信号与供水水头的相关系数为-0.794 1,同样可以判定第一个源信号为物理漏损流量,第二个源信号为用水流量. 经过水平衡方程求解,得σY为185.90、σL为8.25,所得各时刻物理漏损流量如图10所示.将所得结果按照式(20)进行节点流量分配,修正用水规律后的节点流量分配如图11所示. 由图11可知,使用修正后的用水规律进行节点流量分配时,各时刻分配的流量均小于流量计计量的供水总流量,算出的差值流量均为正数. 另外,差值流量与水头有较好的正相关关系,一定程度上反映了物理漏损流量与水头的正相关性规律.

图8　供水管网观测数据Fig.8　Observational data of water distribution network

图9　源信号的模拟结果Fig.9　Simulation results of source signals

上面的举例用的是单一的居民类用水规律,实际该项目实施中要用到12类用水规律并进行综合修正,其复杂程度要高出很多.使用物理漏损流量分析模型求出各时刻物理漏损流量,用该结果作为用水规律修正时的参考,实施过程中发现,使用修正过的用水规律较原始的用水规律,水力模型模拟精度有明显改善.

图10　模拟的物理漏损流量Fig.10　Simulated value of leakage discharge

图11　修正的节点流量分配状况Fig.11　Correctional status of node demand distribution

7结语

基于FastICA算法的物理漏损流量分析模型,是对供水管网运营数据高阶统计信息的应用.该模型输入参数少、易于获取,能有效回避物理漏损流量与水头关系的复杂性.模型可反映出物理漏损流量与水头关系的不确定性.在单水源供水管网中,模型适用性能好,具有较高的模拟准确度.模型在供水管网水力模型的节点流量分配中得到了较好地应用.使用新方法、新理论较为准确地分析供水管网漏损问题，可有效服务于供水管网控制漏工作.本文借助信号处理领域的理论、方法对物理漏损流钽进行了初步研究并得到一定成效，该领域其他算法(例如：CICA算法、小波分析算法)也有助于分析该类问题，随着研究的深入将逐步解决供水管网漏损分析问题.

参考文献(References)：

[1] THORNTON J, LAMBERT A. Progress in practical prediction of pressure: leakage, pressure: burst frequency and pressure: consumption relationships [C]∥ Proceedings of IWA Special Conference-Leakage, Halifax: [s. n.], 2005: 12-14.

[2] FERRANTE M, MASSARI C, BRUNONE B, et al. Experimental evidence of hysteresis in the head-discharge relationship for a leak in a polyethylene pipe [J]. Journal of Hydraulic Engineering, 2010, 137(7):775-780.

[3] CASSA A M, VAN ZYL J E, LAUBSCHER R F. A numerical investigation into the effect of pressure on holes and cracks in water supply pipes [J]. Urban Water Journal, 2010, 7(2): 109-120.

[4] CASSA A M, VAN ZYL J E. Predicting the head-area slopes and leakage exponents of cracks in pipes [C]∥ Urban Water Management: Challenges and Oppurtunities-11th International Conference on Computing and Control for the Water Industry, CCWI. Exeter: CCWI, 2011: 2.

[5] PAOLA F D, GIUGNI M. Leakages and pressure relations: an experimental research [J]. Drinking Water Engineering and Science Discussions, 2012, 5(1): 403-419.

[6] FERRANTE M. Experimental investigation of the effects of pipe material on the leak head-discharge relationship [J]. Journal of Hydraulic Engineering, 2012, 138(8): 736-743.

[7] JAUMOUILLÉ E, PILLER O, VAN ZYL J E. Advantages of a hydraulic saint-venant type model with pressure-dependent leakage [C]∥ Proceedings of the 10th Annual Water Distribution Systems Analysis Conference, WDSA. Kruger National Park: WDSA, 2009: 814-823.

[8] WU Z Y, BURROWS R, MOORCROFT J, et al. Pressure-dependent leakage detection method compared with conventional techniques [J]. Water Distribution System Analysis, 2010: 1083-1092.

[9] WALSKI T, BEZTS W, POSLUSZNY E T, et al. Modeling leakage reduction through pressure control [J]. Journal of American Water Works Association, 2006, 98(4): 147-155.

[10] VAN ZYL J E, CLAYTON C R I. The effect of pressure on leakage in water distribution systems [J]. Proceedings of the Institution of Civil Engineers: Water Management, 2007, 160(2): 109-114.

[11] MENICONI S, BRUNONE B, FERRANTE M, et al. Numerical and experimental investigation of leaks in viscoelastic pressurized pipe flow [J]. Drinking Water Engineering and Science, 2013, 6(1): 11-16.

[12] TABESH M, YEKTA A H A, BURROWS R. An integrated model to evaluate losses in water distribution systems [J]. Water Resources Management, 2009,23(3): 477-492.

[13] BURNELL D, RACE J. Water distribution systemsanalysis: patterns in supply-pipe leakage [C]∥ Joint Conference on Water Resource Engineering and Water Resources Planning and Management 2000: Building Partnerships. Minneapolis: American Society of Civil Engineers, 2004: 104.

[14] WU Z Y, FARLEY M, TURTLE D, et al. Water Loss Reduction [M]. Pennsylvania: Bentley Institute Press, 2011: 32-57.

[15] 朱世泰. 城市供水管网模型校核参数的研究[D]. 广州:华南理工大学, 2014: 5-11.

ZHU Shi-tai. Study on calibrated parameters of urban water distribution system model [D]. Guangzhou: South China University of Technology, 2014: 5-11.

[16] CHEUNG P B, GIROL G V, ABE N, et al. Night flow analysis and modeling for leakage estimation in a water distribution system [C]∥ Integrating Water Systems-Proceedings of the 10th International on Computing and Control for the Water Industry, CCWI 2009. Sheffield: CCWI, 2010: 509-513.

[17] 张冬,李淑慧,张俊杰.优化管网压力以降低管网漏损的研究[J]. 中国给水排水, 2014, 30(3): 59-61.

ZHANG Dong, LI Shu-hui, ZHANG Jun-jie. Optimization of water distribution network pressure for educing leakage [J]. China Water and Wastewater, 2014, 30(3): 59-61.

[18] ALMANDOZ J, CABRERA E, ARREGUI F, et al. Leakage assessment through water distribution network simulation [J]. Journal of Water Resources Planning And Management, 2005, 131(6): 458-466.

[19] YUAN X, WANG C, JI F, et al. A magnetic flux leakage analysis model based on finite element neural network [J]. Insight-Non-Destructive Testing and Condition Monitoring, 2011, 53(9): 482-486.

[20] MASSARI C, FERRANTE M, BRUNONE B, et al. Is the leak head-discharge relationship in polyethylene pipes a bijective function？ [J]. Journal of Hydraulic Research, 2012, 50(4): 409-417.

[21] 于先川, 胡丹. 盲源分离理论与应用[M]. 北京: 科学出版社, 2011: 17-52.

[22] 金羽晔, 李式巨, 王彦波, 等. CDMA 盲自适应独立分量多用户检测器[J]. 浙江大学学报: 工学版, 2008, 42(10): 1745-1750.

JIN Yu-te, LI Shi-ju, WANG Tan-bo, et al. Independent component analysis based blind adaptive multiuserdetector for CDMA [J]. Journal of Zhejiang University: Engineering Science, 2008, 42(10): 1745-1750.

[23] 周晓峰, 杨世锡.基于负熵最大化的机械振源半盲分离方法[J]. 浙江大学学报: 工学版, 2011, 45(5): 846-850.

ZHOU Xiao-feng, YANG Shi-xi. Semi-blind sources separation of mechanical vibrations base on maximization of negentropy [J]. Journal of Zhejiang University: Engineering Science, 2011, 45(5): 846-850.

[24] ALMANDOZ J, CABRERA E, ARREGUI F, et al. Leakage assessment through water distribution network simulation [J]. Journal of Water Resources Planning and Management, 2005, 131(6): 458-466.

[25] TABESH M, TANYIMBOH T T, BURROWS R. Head-driven simulation of water supply networks [J]. International Journal of Engineering, 2002, 15(1): 11-22.

[26] 顾军,胡显丹.基于FastICA 算法的敌我识别信号分选方法研究[J].舰船电子对抗, 2009, 32(5): 41-44.

HU Jun, HU Xian-dan. Research into the sorting method of IFF signals based on fastICA algorithm [J]. Shipboard Electronic Countermeasure, 2009, 32(5):41-44.

[27] 蒋夕平, 吴凤凰, 蒋昱, 等. 基于 FastICA 算法的高光谱矿物丰度反演[J]. 吉林大学学报:地球科学版, 2013, 43(5): 1681-1686.

JIANG Xi-ping, WU Feng-huang, JIANG Yu, et al. Hyper-spectral mineral abundance inversion based on FastICA algorithm [J]. Journal of Jilin University: Earth Science Edition, 2013, 43(5): 1681-1686.

收稿日期：2015-04-10.

基金项目：广东省教育部产学研结合资助项目(重大专项)(2011A090200040)；国家自然科学基金资助项目(51278148)；欧盟第七框架“玛丽·居里行动”计划(PIRSES-GA-2012-318985).

作者简介：郑成志(1985—),男,博士生,从事供水管网模拟及其优化研究. ORCID: 0000-0002-9300-2683. E-mail: buye3000@163.com 通信联系人: 高金良,男,副教授,博士.ORCID: 0000-0002-6662-0187. E-mail: gjl@hit.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.06.004

中图分类号：TU 991.3

文献标志码：A

文章编号：1008-973X(2016)06-1031-09

Leakage discharge analysis model based on FastICA algorithm

ZHENG Cheng-zhi1, GAO Jin-liang1, HE Wen-jie1,2

(1.SchoolofMunicipalandEnvironmentalEngineering,HarbinInstituteofTechnology,Harbin150090,China;2.TianjinWaterWorksGroupCo.Ltd,Tianjin300040,China)

Abstract:A new leakage discharge analysis model based on fast independent component analysis (FastICA) algorithm was established in order to solve the problems of the traditional leakage discharge analysis models, such as low simulation accuracy, incapability of reflecting the uncertain relationship between leakage discharge and presssure head and so on. The model divided total water supply flow into actual consumed water flow and leakage discharge and considered them as two source signals. In the model, the total water supply flow and pressure head at the entrance were considered as two input parameters. The waveform information of two flows were obtained by separating source signals. The order of the source signals was determined by comparing the correlation coefficients. The real amplitude of leakage discharge was solved out according to the flow balance equation. Therefore, the leakage discharge was simulated in time series. For this model, the input parameters are easily getparms. It can effectively avoid the complexity of the relationship between leakage discharge and head pressure. Thus the simulation accuracy is high in the water distribution system with one entrance only. The model has been preferably applied in the node demand distribution of one water distribution network’s hydraulic model.

Key words:water distribution network；physical loss； FastICA algorithm