异构信息网上的可达性查询

尹 丹 高 宏 邹兆年 李建中

（哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001）（yindan630＠163．com）

异构信息网上的可达性查询

尹 丹 高 宏 邹兆年 李建中

（哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001）（yindan630＠163．com）

随着图数据规模的爆炸式增长，其形式也越来越复杂．异构信息网可建模成包含多种类型的顶点和多种类型的边的图．例如，文献数据库、在线购物网站等．首次研究异构信息网上的可达性查询问题．利用不同类型顶点之间的关系，查询2个顶点满足路径模式的可达性，该问题的时间复杂度是多项式的．然而在大规模的网络上，每次查询遍历一遍网络的时间开销也是不能容忍的．现有的可达性查询问题主要分为2类：k跳可达性查询和带有标签约束的可达性查询．但是这2种问题的算法都不能用于解决异构信息网上的可达性查询问题．因此，为了实现高效的在线查询，提出一种新的索引结构，通过路径模式的分解，预先计算部分路径模式的可达信息．当在线查询到来时，在路径模式的偏序图上，快速找到索引结构中存在的路径子模式，高效地计算查询结果．在真实和人工数据集上进行了大量实验，验证了算法的有效性．

异构信息网；查询处理；可达性；路径模式；索引

近年来，越来越多的图数据出现，如社交网络、生物网络、传感器网络和Web图等．与此同时，图数据的规模也呈爆炸式地增长．截止2014年6月，全球最大的社交网络Facebook已有超过13亿个用户．随着图数据规模的爆炸式增长，其形式也越来越复杂．现实世界中实体不仅仅是单纯的一种类型，很多时候多种类型的实体同时存在一个网络中，同时，联系也不仅仅存在于同一类型的实体内部，在不同类型的实体之间同样也存在着关系．异构信息网可以建模成图模型，其包含多种类型的顶点和多种类型的边．文献数据库、在线购物网站、物联网等都可以看成是异构信息网．在这些网络中，顶点类型多种多样，不同类型顶点之间的连接关系也不同．

例1．图1是一个异构信息网的实例，来自互联网电影数据IMDb．该网络中，共有4种类型顶点，分别是演员（A）、电影（M）、导演（D）和电影公司（S）．其中，共存在4种顶点间关系，分别是演员与电影之间的参演关系、导演与电影之间的指导关系、电影与电影公司之间的投资关系以及演员之间的合作关系．例如，Leonardo参演了电影Titanic和Inception，其中Titanic的导演是Cameron，该导演又指导了电影Avatar，同时，电影Titanic的投资公司是20th Century Fox和Paramount．

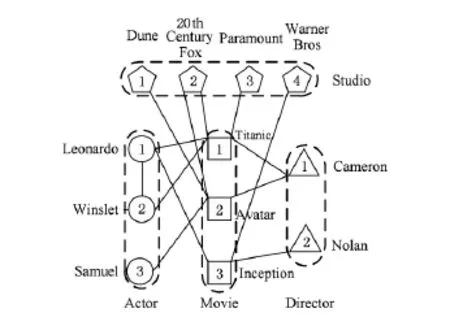
Fig．1 IMDb heterogeneous information network．图1 IMDb异构信息网

可达性查询是检验是否存在一条路径，从一个顶点到达另一个顶点，是图分析中一个基本的操作．分析异构信息网可以得到的信息远远大于同构信息网．在异构信息网上的可达性查询可以挖掘现实世界中大量潜在的有用信息．通过不同类型顶点之间的关系，挖掘与结构有关系的信息，进而提供有用的内在信息给用户决策．

异构信息网上基于路径可达性查询可定义为如下形式：查询从源顶点s出发，经过路径P模式，是否可以到达目标顶点t．

例2．异构信息网上基于路径模式的可达性查询．

查询1．查询Cameron是否指导由Leonardo参演的电影．这个查询可以表达成异构信息网上基于路径的可达性查询，源顶点是导演Cameron，目标顶点是演员Leonardo，路径模式是“D→M→A”．

查询2．查询Leonardo与Samuel参演的电影是否为同一导演Cameron执导．这个查询可以表达成异构信息网上基于路径的可达性查询，源顶点是演员Leonardo，目标顶点是演员Samuel，路径模式“A→M→D→M→A”．在原始图中，Leonardo与Samuel没有边，但是二者在路径模式“A→M→D→M→A”上是可达的．

查询3．查询演员Leonard与Winslet是否参演过同一部电影，此电影是由Warner Bros公司出品．在该查询中，源顶点是演员Leonardo，目标顶点是演员Winslet，路径模式是“A→M→S→M→A”．在原始图中，Leonardo与Winslet之间存在边，然而该查询中二者是不可达的，因为他们没有合作的电影是Warner Bros出品．

异构信息网上的可达性查询反映了2个顶点在给定路径模式下是否可达，与原始图中这2个顶点之间是否有边无关．原始图中的2个顶点之间存在边，在给定路径模式上不一定可达．相似地，原始图中没有边的2个顶点在给定路径模式可能是可达的．不同于传统的可达性查询问题中只关于顶点之间是否存在路径，异构信息网上的可达性查询问题可以深入挖掘顶点之间的联系，对于分析和挖掘异构信息网络有重大意义．因此本文提出了异构信息网络上基于路径模式的可达性查询问题．

图上的可达性查询问题已经有很多的研究成果．但是目前还没有异构信息网上的可达性查询的研究．以往的关于可达性查询的研究工作主要集中在传统的同构图上，这些方法并不能应用到异构信息网上．同时以往工作的可达性查询大多数都是建立在有向无环图（directed acyclic graph，DAG）上的，而在异构信息网上，环路是经常存在的．我们可以通过将异构信息网中的强连通组件压缩成一个顶点，将异构信息网转化成DAG．然而，这就会丢失不同类型顶点之间的路径信息，因此我们无法通过传统的方法将异构信息网转化成DAG．这些挑战都是本文要解决的问题．

本文研究一种新类型的可达性查询，在异构信息网络上，给定源顶点、目标顶点以及路径，查询从源顶点出发，经过给定路径模式，是否可以到达目标顶点．

本文的主要贡献总结如下：

1）本文首次研究了异构信息网上可达性查询问题，利用不同类型顶点之间的关系，查询2个顶点间是否满足路径的可达性，该问题的时间复杂度是多项式的；

2）随着网络规模爆炸式的增长，在线查询中，每个查询都遍历一遍网络的时间开销是不能容忍的，因此，为了能够快速响应在线查询，本文提出一种新的索引结构，预先计算部分路径模式的可达信息，通过路径模式的分解，共享部分子路径模式的可达信息；

3）通过构建路径模式的偏序图，提出了贪心的路径模式选择策略，选择出部分路径模式，用于构建索引结构，计算其可达信息并存储；

4）提出了高效的在线查询处理算法，将查询模式分解成预计算的路径模式，利用其可达信息，快速地将查询结果返回给用户，提高了在线查询效率；

5）在真实和人工数据集上进行了大量的实验，验证了算法的有效性．

1 相关工作

同构图上的可达性查询已经有很多研究成果［1］，但是现有的算法都不能应用到异构信息网络上．

最短路径查询［2－5］只涉及顶点之间的最短路径，不能区分路径经过哪类顶点．k跳可达性查询［6－11］是计算顶点之间的最短路径是否小于等于k，是最短路径查询问题的扩展．它们都无法用于挖掘异构信息网上顶点间丰富的关系．

带有标签约束的可达性查询［12－14］是计算2个顶点之间路径上的边的标签集合是否属于给定的标签集合．本文研究的异构信息网上顶点的可达性要求路径上标签的顺序是预先规定的（即路径模式），因此无法用带标签约束的可达性问题解决本文研究的问题．

异构信息网上基于路径模式的可达性查询可以看作是特殊的子图匹配问题［15－17］．然而，子图匹配问题是NP完全的，算法的代价高于本文研究的问题，并不适合解决异构信息网上的可达性查询问题．

现有的异构信息网上的研究工作大多数来自于Sun［18－22］．文献［18］搜索异构信息网中top－k相似对象，文献［19］是关于异构信息网络中的链接预测问题的研究，文献［23］研究了异构信息网上基于网页文本的实体识别问题．这些都无法解决异构信息网上的可达性查询问题．

2 问题描述

定义1．异构信息网．异构信息网是一个有向图G＝（V，E，T，R， ，φ），其中V是顶点集合，E V× V是边集合，T是顶点类型集合，R是边类型集合， ：V→T是从顶点集合V到顶点类型集合T的映射函数，φ：E→R是从边集合E到边类型集合R的映射函数．

图1是一个异构信息网实例．现实世界中还有很多异构信息网的实例，比如商品购物网站、多媒体分享网站等．

定义2．网络模式．图TG＝（T，R）是异构信息网G＝（V，E，T，R， ，φ）的模式，其中T是G中的顶点类型，有向边集R是G中顶点之间的关系．

定义3．路径模式．网络模式TG＝（T，R），P＝是定义在TG上的路径，Ti是顶点类型，Ri是从Ti到Ti＋1的关系．R1R2…Rl－1定义了T1到Tl复合关系．

异构信息网的网络模式给出了在异构信息网中的顶点类型和顶点间的关系．每个异构信息网是其网络模式的一个实例．如图2是图1所示的IMDb网的网络模式，图1是图2的一个实例．

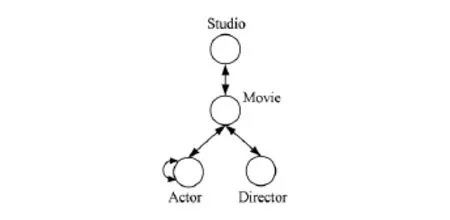
Fig．2 IMDb network schema．图2 IMDb网络模式

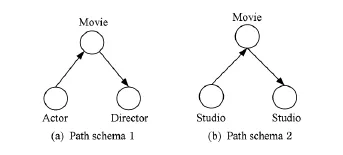
Fig．3 Examples of path schema．图3 路径模式举例

定义4．顶点可达性．异构信息网G＝（V，E，T，R， ，φ）， s，t∈V，s是源顶点，t是目标顶点，路径模式P＝T1→T2→…→Tl， （s）＝T1， （t）＝Tl，若存在路径p是P的实例，从s出发经路径p到达t，定义为s→Pt．

此处我们定义异构信息网络上可达性查询的形式为Q＝（s，t，P），其中s是源顶点，t是目标顶点，P是路径模式．

异构信息网上基于路径模式可达性查询（path reachability query，PRQ）的问题定义如下．

输入：异构信息网G＝（V，E，T，R， ，φ），可达性查询Q＝（s，t，P），其中路径模式P＝T1→T2→…→Tl， （s）＝T1， （t）＝Tl；

输出：s→Pt是否成立，若成立，则输出s和t之间的所有路径实例．

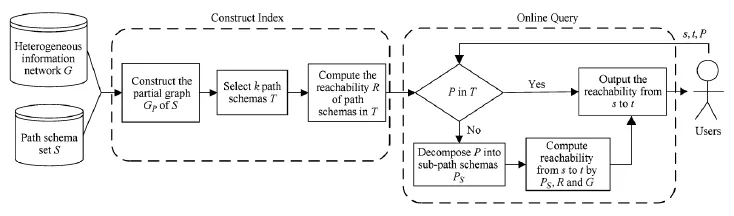
Fig．4 System framework．图4 系统框架图

解决PRQ问题最简单的方法是深度优先或广度优先搜索．从顶点s出发，搜索T2类型的顶点，a2是s的邻接顶点，若 （a2）＝T2，且（s，a2）∈E．从a2出发，搜索T3类型的顶点，计算a2的邻接顶点．递归此过程，直到访问完路径模式P上的所有路径实例．若s→Pt，找出s到t的所有满足路径模式P的实例，否则s到t不可达．

定理1．异构信息网上PRQ问题的时间复杂度是PTIME．

证明．异构信息网上PRQ问题可通过遍历一遍异构信息网中与查询中路径模式相关的顶点和边即可得到问题的解，因此该问题时间复杂度是O（｜V｜＋｜E｜），其中V是顶点集合，E是边集合，因此PRQ问题的时间复杂度是PTIME．证毕．

然而，当网络的规模非常大时，每种类型的顶点数量达上百万甚至更多，边的个数更多，遍历一遍这些顶点的时间开销非常大．这种遍历方法无法快速地响应在线查询．因此，本文研究如何高效地处理异构信息网上的在线可达性查询．我们通过构建索引，预先计算出一部分路径模式上顶点的可达性信息，当在线查询到来时，通过将查询的路径模式分解，利用预先计算的索引来快速地响应查询，系统框架如图4所示．下面我们将详细介绍算法的实现过程．

3 索引构建

3．1 路径模式分解

定义6．路径模式偏序关系．给定网络模式TG＝（T，R），路径模式P1＝Ti→Ti＋1→…→Tj和路径模式P2＝T1→…→Ti→…→Tj→…→Tl，其中1≤i≤j，1≤j≤l．那么存在偏序关系P1P2，我们说P2包含P1或P1包含于P2．

由定义6可知偏序关系具有传递性．

定义7．路径模式分解．给定异构信息网G＝（V，E，T，R， ，φ）上的路径模式P＝T1→T2→…→Tl，P1，P2，…，Pk是k个包含于P的路径模式，满足P＝P1P2…Pk．其中“”表示路径模式Pi中最后一个顶点类型和Pi＋1中第1个顶点类型间关系的合成操作．同时，定义路径模式P可分解成P1P2…Pk．

通过将路径模式P分解为其包含的若干个不相交的子路径模式，在每个子路径模式上计算所有顶点对的可达性．当查询顶点对s和t之间经由路径模式P的可达性时，其中 （s）＝T1， （t）＝Tl．从s出发，通过连接子路径模式上关于s和t的可达顶点对，可得到s到t之间关于模式P的路径实例．

例3．图5给出一个包含5种类型顶点的异构信息网．对于路径模式P＝T1→T2→T3→T4→T5，一种分解方法是P1P2，其中P1＝T1→T2，P2＝T3→T4→T5．表1和表2分别给出了路径模式P1和P2上可达顶点对的路径实例．当查询源顶点是1，目标顶点是22，路径模式是P．我们可以利用路径模式P的分解子模式的可达性信息，来得到1和22的可达性．从路径模式P1的可达性信息知，顶点1到8可达，经过路径1→8，从图5知顶点8与T3类型的14顶点间右边．由路径模式P2可达性信息知14到22可达，经过路径14→18→22，那么顶点1到22可达，经过路径1→8→14→18→22．由此可见，通过路径模式分解，可以利用子路径模式的可达性信息计算查询结果，大大减少了在线查询的计算量．

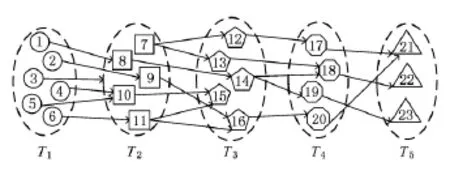
Fig．5 An example of heterogeneous information network．图5 异构信息网实例

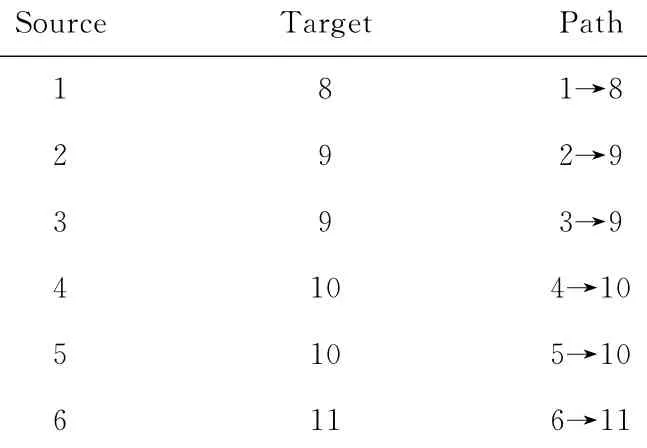
Table 1 Reachability of Path Schema 1表1 路径模式1的可达信息

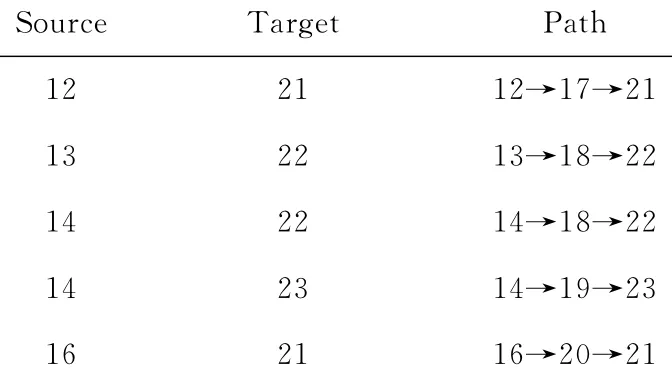
Table 2 Reachability of Path Schema 2表2 路径模式2的可达信息

通过预先计算出一部分子路径模式的可达结果，可减少在线查询中每个查询的计算量，可大大提高在线的查询响应效率．由于子路径模式的可达性信息在不同查询中可以重复利用，因此我们可以构建少量路径模式的可达信息作为索引结构，进一步降低在线查询的响应时间．

3．2 路径模式选择

每个路径模式都包含多个子路径模式，其分解方法也有多种．不同的路径模式分解后共享部分子路径模式，这部分子路径模式的可达信息只需要在预计算时计算一遍，当查询到来时就不需要计算这部分信息．如果预先将所有的路径模式的可达信息进行预计算并存储，可以最快地响应查询．但是，这需要耗费指数级的存储空间，显然是不可行的．因此我们需要选择出一部分路径模式进行索引的构建，使得在线查询计算代价最小．因此最小化查询平均查询响应时间，快速地响应在线查询．下面就详细介绍如何选择这部分子路径模式进行可达信息计算．

给定异构信息网G＝（V，E，T，R， ，φ），其路径模式可按长度划分为l类（假设G上最长的路径模式长度为l）：其中Mi（1≤i≤l）表示长度为i的路径模式集合，｜Mi｜表示Mi中路径模式的个数．

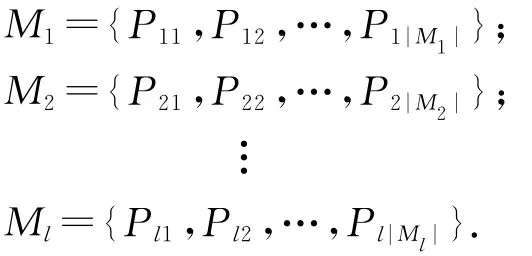
例4．图6给出一个网络模式，其中有6种类型的顶点，最长路径模式的长度为4．该网络模式的路径模式如下：

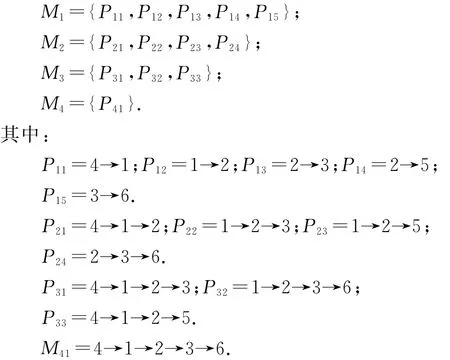
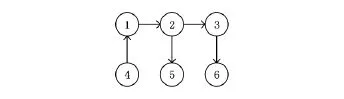
Fig．6 An example of network schema．图6 网络模式实例

根据路径模式之间的偏序关系，可以得到路径模式的偏序图．

例5．图7是图6所示的异构信息网的路径模式偏序图．图7顶点为异构信息网络中所有的路径模式，且路径模式按照其长度分层．在图7中，顶点分为5层，分别是M0，M1，M2，M3，M4，其中M0是长度为0的路径模式，即路径模式中只含有一个顶点类型．对于处于相邻层的2个路径模式P1和P2，若存在偏序关系P1P2，那么在偏序图中，存在一条有向边从P1指向P2．例如P11＝4→1，P21＝4→1→2，存在P11P21，则有一条有向边从P11指向P21．

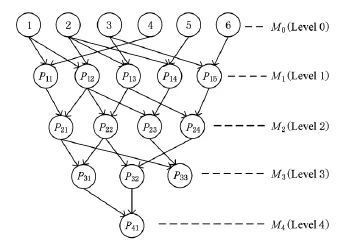
Fig．7 Partial order graph of path schemas．图7 路径模式偏序图

构建路径模式的偏序图大致思想如下：异构信息网G和G上的路径模式集合S，首先将S中的路径模式按照长度划分为l＋1层（假设最长的路径模式长度为l）M0，M1，…，Ml；将S中的路径模式作为偏序图的顶点集合．若相邻2层的路径模式存在偏序关系，那么有一条有向边从低层顶点指向高层顶点．

下面给出构建路径模式偏序图ConPOG算法的伪代码．

算法1．ConPOG算法．

输入：异构信息网G＝（V，E，T，R， ，φ）及G的路径模式集S；

根据路径模式的长度将路径划分为l＋1层（假设最长的路径模式长度为l），其时间开销是路径模式的个数O（｜S｜）（行①）．将路径模式作为偏序图的顶点，偏序图的边集初始化为空集，时间复杂度是线性的O（1）（行②）．计算偏序图的边集，对于相邻2层的路径模式对P1，P2，P1∈Mi，P2∈Mi＋1，如果有偏序关系P1P2，那么存在一条有向边从P1指向P2（行③～⑤）．判断P1和P2是否存在偏序关系P1P2的时间复杂度是路径模式P2的长度，其时间复杂度为O（l）（行④）．这个过程最多循环｜S｜2次，所以时间复杂度为O（l｜S｜2）．最后输出偏序图（行⑥）．综上所述，ConPOG算法的时间复杂度为O（l｜S｜2）．

预先计算并存储所有路径模式的可达信息需要海量的存储空间，这是不可行的．因此，我们可以预先计算部分路径模式，当在线查询到来时，通过利用预计算的这部分路径模式上的顶点可达性信息和查询中路径模式的分解，得到查询结果．下面，我们就详细研究如何从路径模式偏序图中选取这部分预计算的路径模式．

假设异构信息网上的可达性查询Q＝（s，t，P）中s，t，P都是随机选取的，符合均匀分布，那么用户的查询所选取的路径模式是等概率的．从偏序图中选取k个路径模式进行预计算构建索引，使在线查询的平均响应时间最短，即所有路径模式的顶点可达查询的平均计算代价最小．这个问题可由顶点覆盖问题规约过来，是NP完全的．因此本文针对路径模式选择问题给出启发式的贪心选择策略，由于贪心算法的执行过程简单，可以缩短索引构建的时间，因此贪心策略的选择是必要的．

由路径模式的偏序图可知，出度越大顶点所代表的路径模式可以被越多的路径模式所包含，预先计算这部分路径模式，可以被更多的查询利用预计算的可达信息，因此贪心地选择这些路径模式构建索引是可行的，能够大大加快查询速度．同时，对于一个路径模式的分解，其分解的子路径模式个数越少，子路径模式越长，那么计算的开销就越小．因此当偏序图中2个顶点的出度相等时，应优先选择长度长的路径模式．

首先调用构建偏序图ConPOG算法生成路径模式偏序图，时间开销是O（l｜S｜2）（行①）．根据偏序图中顶点的出度，将长度大于0的路径模式降序排序，时间复杂度为O（｜S｜）（行②）．当2个路径模式出度相等时，长度较长的路径模式排在前面，时间复杂度为O（｜S｜）（行⑤～⑦）．选择排序列表中前k个路径模式T作为要预计算可达性信息的路径模式（行⑧），需要O（1）时间．下面，就为每个T中的路径模式计算可达性信息（行⑨～ 瑐瑦）．对于T的路径模式P，初始化G中所有顶点为标签为unfinded，P的可达信息表RP为空集，时间开销为O（｜V｜）（行⑩ 瑏瑡）．对于P中第1个顶点类型的任意顶点u，构建一棵以u为根、高度为O（｜P｜）的树T，用于存放所有u出发，路径模式P上的路径实例（行 瑏瑢～ 瑐瑦）．首先初始化T为空，把u作为T的根，u顶点标记为finded，时间开销为常数O（1）（行 瑏瑣～ 瑏瑥）．对于P中第2个顶点类型的任意顶点w，若存在边（u，w），把w作为u的儿子插入T中，标记w为finded，需要时间为第1个顶点类型和第2个顶点类型之间边集合大小O（E（T1，T2））（行 瑏瑦～ 瑏瑩）．对于P中相邻2个类型顶点 w， （w）＝Ti， v， （v）＝Ti＋1，若w的标签为finded（即在树T中），若存在（w，v）∈E，那么就将v作为w的儿子插入T中，且标记v为finded，时间开销为O（E（T2，T3）＋E（T3，T4）＋，…，＋E（Tj－1，Tj））（行 瑐瑠～ 瑐瑥）．那么行 瑏瑢～ 瑐瑥时间开销为O（E（T1，T2）＋E（T2，T3）＋，…，＋E（Tj－1，Tj））），我们可以写成O（｜E｜）．最后将T中所有长度为｜P｜的路径存放到P的可达信息索引中，其时间复杂度为O（｜V｜＋｜E｜）（行 瑐瑦）．那么，行⑨～ 瑐瑦总的时间代价为O（k（｜V｜＋｜E｜））．输出k个路径模式的可达信息索引为常数时间（行 瑐瑧 瑐瑨）．因此构建索引ConIndex算法的时间复杂度是O（k（｜V｜＋｜E｜））．

4 在线可达性查询处理

本节介绍如何利用第3节构建的可达信息索引快速有效地响应在线的PRQ．用户输入查询Q＝（s，t，P），其中s是源顶点，t是目标顶点，P是路径模式，查询s到t是否存在路径实例满足路径模式P．若存在，则输出所有的路径实例，不存在则s到t经过路径模式P不可达．

对于一个查询的路径模式，需要按照预计算的索引结构进行分解，连接预计算的子路径模式可达信息，快速地计算出s到t的可达性．下面详细描述如何根据预计算的索引结构将路径模式P分解．模式P有很多分解方法，分解子路径模式包含的预计算路径模式越多，且分解的子路径模式越长，合并子路径模式的操作越少，时间就越快，在线响应时间就越短．因此，在偏序图中，我们贪心地选择P的预计算祖先中长度最长的子路径模式作为其分解子模式，然后从P中去掉这部分子模式，递归地进行这个过程，直到P为空．最后将这些预计算的路径模式上起始顶点为s、目标顶点为t的路径实例根据原始图的边连接起来，就得到查询结果．这里，需要说明的是，偏序图的第0层是长度为0的路径模式，即原始图中的顶点类型，根据预计算的路径模式将P进行分解，当P包含的子路径长度大于0的路径模式不能连接构成P，分解的子路径模式中就需要包含第0层顶点．

搜索查询中的P是否在索引中存在，耗费时间O（k）（行①）．若存在，直接输出索引中的源点为s，目标顶点为t的路径实例，时间复杂度为路径模式P的索引表大小O（｜R｜）（行②～④）．如不存在，执行以下过程．首先，在偏序图上搜索P的预计算路径子模式（行⑤～ 瑏瑦）．初始化变量时间开销为O（1）（行⑤～⑦）．路径模式P所在层数为第｜P｜层，我们贪心的搜索P最长的路径子模式，从｜P｜－1层开始搜索是否有P的子模式在索引中，若有模式R满足RP，那么将R加入P的子模式集合Ps中，从P中去掉关于R的顶点类型和关系得到模式W，继续搜索W的子路径模式，直到W为空集，若｜P｜－1层不存在P的子路径模式，那么向上搜索｜P｜－2层，直到第0层，此过程的时间复杂度是O（｜P｜）（行⑧～ 瑏瑦）．将Ps中路径模式按照其第1个顶点类型编号升序排列U1，U2，…，Uk，那么将这k个路径模式连接起来就是P．这个过程需要O（｜P｜）时间（行 瑏瑧）．对于U1的可达信息索引表中，搜索源顶点是s的路径实例集合I，若U1长度为0，那么I就是s顶点，其时间开销为U1的索引表R大小O（｜R｜）（行 瑏瑨）．从i等于1开始，对于相邻的2个路径模式Ui和Ui＋1，I中的任意长度为｜Ui｜＝m的路径实例p＝（p1，p2，…，pm）若在Ui＋1的可达信息索引表中存在源顶点是pm的路径实例（q1，q2，…，qn）（pm＝q1），则将插入I中，这个过程的时间开销是O（（k－1）｜R｜2）（假设每个索引的大小是｜R｜）（行 瑐瑠～ 瑐瑧）．最后将I中目标顶点不是t的路径实例删除，并输出PI，其时间开销为O（｜I｜）（行 瑐瑨～ 瑑瑡）．综上所述，在线查询处理算法的时间复杂度为O（｜P｜）＋O（k｜R｜2）．该算法的时间开销与路径模式长度与索引大小有关．

5 实 验

本节给出算法在真实和人工数据集上的实验结果．实验环境为Windows PC机，Intel?Core i5－2400CPU 3．1GHz，4GB内存．实验运行编译环境是Microsoft Visual Studio 2010，编程用C语言实现．

5．1 实验数据集

1）DBLP数据集

本文用到的数据是2008年从DBLP网站下载的数据中提取的［18］，并由此构建了异构信息网，形式如图8所示．该网络包含5种类型顶点：论文（Paper）、作者（Author）、会议（Conference）、关键词（Term）和领域（Field）．本文使用4个领域的相关主要会议所发表的全部论文，这4个领域分别是：数据库（DB）、数据挖掘（DM）、人工智能（IR）和信息检索（AI），相关主要会议分类如表3所示．同时4种类型的边存在于该网络中，它们是：论文与作者之间的写作关系、论文与会议之间的发表关系、论文与关键词之间的所属关系和会议与领域之间的分类关系．本文用到的数据集包含28 702位作者在他们这20个会议上所发表的全部论文28 569篇．数据集中共含有13 575个关键词．在该网络中，作者与文章之间存在74 632条边、论文与会议之间存在28 569条边、论文与关键字之间存在229 187条边以及会议与领域之间的20条边．

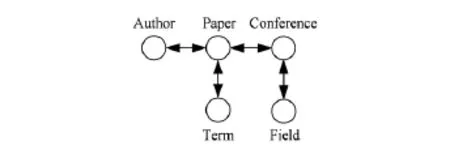
Fig．8 DBLP heterogeneous information network．图8 DBLP异构信息网

Table 3 Categories of Main Conferences表3 主要会议领域划分

2）人工数据

为了验证本文提出算法在大规模、多类型的异构信息网上的效率，我们人工合成数据来实验验证．实验中，我们生成了包含20种不同类型顶点和40种不同类型的边的随机图．首先加入2种类型顶点，并把这2种类型相连．然后，每次加入一种新类型顶点，并随机选择一种已存在的顶点类型与其相连，直到20种类型顶点都被加入．在20种顶点类型中，随机选择21个不连接的顶点类型对，将其连接得到20种顶点类型和40种不同类型的边．初始化每种顶点类型包含10万个顶点，为了保证不同类型顶点之间的连通性，设定网络的密度为｜｜＝2．对于任｜｜意2个相连的顶点类型Ti和Tj，随机选择10万个顶点对u，v，u∈Ti，v∈Tj，将边（u，v）加入到网络中．最后得到网络共包含200万个顶点和400万条边．

5．2 DBLP数据实验结果

我们从索引的构建时间、索引规模和查询响应时间3个方面在DBLP数据集上验证算法的效率．在查询响应时间衡量上采用图上的深度优先搜索DFS算法作为对比算法，从源顶点出发，沿着路径模式上不同类型的顶点进行深度优先搜索，找出所有源顶点到目标顶点的路径实例．

1）索引构建时间

图9（a）给出了索引构建时间的实验结果．横轴是k值，表示预计算的路径模式个数；纵轴是索引构建的时间，单位是s．随着k值的增大，索引构建时间也增多．在实验中，我们考察当k值从3～7的索引构建时间．由图9（a）可以看出，随着k值的增加，索引的构建时间也增加．这是显而易见的，因为需要计算的路径模式增多．当k值从3增加到7时，索引的构建时间大约从0．1s增长到2．5s．在图9（a）中可看到，当k值从3增加到4，索引的构建时间增加非常少；当k值从4增加到5，索引的构建时间突然增加很大．这是因为实验中所用的DBLP异构信息网络中不同类型顶点的个数差异非常大，并且不同类型顶点间的边数目差距也很大，从而导致k值增加产生的非线性时间开销．

2）索引的规模

图9（b）给出在不同k值情况下索引的规模．横轴是k值，表示预计算的路径模式个数；纵轴是索引规模，单位是MB．在实验中，我们考察当k值从3～7的索引构建时间．由图9（b）可以看出，随着k值的增加，索引的规模也随着增长，因为有更多的路径模式上的顶点可达信息需要存储．当k值从3增加到7时，索引的规模大约从1．1MB增长到7．6MB．由图9（b）可以看出当k值由3变为4，索引的构建时间增加非常少．这是因为增加的路径模式所对应的顶点个数少，因此，当k值由3变为4时索引的规模也增加很少．当由4增加到5时，索引的规模大大增加．

Fig．9 Experimental results on DBLP dataset．图9 DBLP数据实验结果

3）查询效率

我们在DBLP异构信息网络上随机产生PRQ，考察算法在不同情况下的查询效率．图9（c）当查询中路径模式长度不同时，算法的查询响应时间．横轴｜P｜表示查询路径的长度，纵轴表示查询的平均响应时间，实线是本文算法的性能，虚线是对比算法的性能曲线．因为DBLP网络中路径长度最长为3，所以我们考察查询路径模式的长度分别为1，2，3时，算法的在线响应时间．实验中，我们针对每种路径长度，分别随机产生1 000个PRQ，本文的算法中索引规模k取值为5．由图9（c）我们可以看出，当查询路径模式的长度｜P｜从1增加到3时，查询的响应时间大约从0．28s增加到0．57s．路径模式的长度对查询响应的时间影响不可忽略，因为路径模式的分解子模式增多，需要合并的开销也变大．同时，本文的算法的在线查询响应时间明显小于对比算法．因为对比算法每次都需要搜索路径模式上所有顶点类型的顶点，当路径模式从1增加到3时，对比算法的时间开销增加明显大于本文算法．因为路径模式长度增加导致DFS的搜索时间增加，每次查询的时间开销都增加．对于用户大量查询，对比算法的性能明显下降．由图9（c）我们可以看出，当路径模式长度为3时，本文提出算法的平均响应时间比对比算法小0．2s．

图9（d）给出算法在k值不同的情况下查询平均响应时间，横轴表示k值，纵轴表示查询平均响应时间，单位是s．在实验中，我们随机产生1 000个查询．由图9（d）我们可以看出，当k值增加时，查询响应时间也随着变短．因为索引中包含的可达信息增多，在线查询可利用的索引信息增多，计算量减少．当k值从3增加到5时，查询响应时间下降迅速，当k值从5增加到7时，查询响应时间下降缓慢．这是因为当路径模式的出度相等时，我们优先选择长度大的路径模式，较长的路径模式可以减少查询的路径模式的分解个数，降低计算量，而随后增加的预计算路径模式都是长度较短的，对于查询模式的分解贡献小于长度较长的路径模式．

我们同时考察了偏序图的构建时间．本文构建的DBLP异构信息网中包含25个路径模式，网络的偏序图构建时间非常短，因为其网络的路径模式个数比图的规模相比很小，因此构建其偏序图非常快．5．3 人工数据实验结果

为了衡量算法的可扩展性，我们用人工数据考察算法在大规模网络上的执行效率．与在DBLP真实网络上的实验相同，本节我们从3个方面衡量算法的性能．

1）索引构建时间

图10（a）给出了算法在人工数据上索引构建时间．在实验中，我们选取k值从5增加到30且间隔为5的索引构建时间实验结果．从图10（a）可以看出，索引的构建时间随着k值增大而增加，当k＝30时，索引的构建时间大约为60s．因为索引的构建是在查询之前完成，且只构建一次，因此这并不影响查询的效率．

2）索引规模

图10（b）给出算法在人工数据上的索引大小结果．实验中，选取与索引构建时间相同的k取值对比．由图10（b）可以看出，随着k值的增加，索引的空间也变大，当k值增加到30时，索引的规模达到将近50MB．这与大规模的网络相比，还是很小的，且是存储空间可容忍的．索引的规模取决于所选择的路径模式的长度以及路径实例的个数，并不是网络中所有边的加和，因此与网络中总边数没有直接关系．且路径模式长的路径实例个数一定不大于其子路径模式上的路径实例个数．因此真实数据与人工数据的索引规模的比例与原始网络的规模比例没有直接关联．

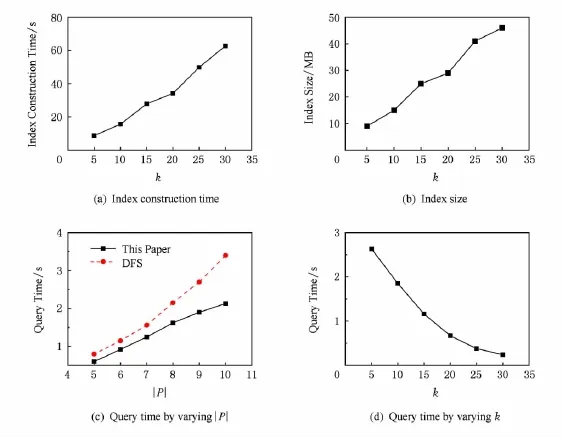
Fig．10 Experimental results on synthetic dataset．图10 人工数据实验结果

3）查询效率

在人工数据上的随机产生可达性查询，考察算法的在线查询响应时间．图10（c）给出当查询中路径模式长度不同时，算法的查询响应时间．横轴｜P｜表示查询模式的长度．实验中，我们取k值为10，且对于每种长度的路径模式，随机产生5 000个PRQ，来考察算法的在线效率．在图10（c）中，虚线表示对比算法的性能，实线是本文提出的算法性能．由图10（c）我们可以看出，与对比算法相比，本文的算法可以更快速地响应用户的在线查询．且当查询的路径长度增加时，对比算法的查询响应时间增长较快，而本文提出的方法的查询时间增加速度较慢．这是因为当路径模式增大时，路径模式可分解的子路径模式也变长，这部分子路径模式的可达信息预先存在索引中，在线查询时算法可以直接利用这部分信息，因此就大大减少了相应的时间．当查询路径模式为10时，对比算法的平均响应时间达到了3．6s，而本文的算法仅为2．1s，每个查询提高了1．5s，对于大规模的在线查询，这就大大提高了效率．

图10（d）给出算法在k值5，10，15，20，25，30时查询的平均响应时间对比结果，实验中我们随机产生5 000个PRQ，用来考察算法的在线效率．由图10（d）我们可以看出，当k值增加时，查询响应时间也随着变短．当k值由5增加到20时查询的时间下降较快，其后趋于平稳下降．因为查询的产生是随机的，因此索引中较长的路径模式对于降低查询的计算量贡献较大．当k值为5时，查询的平均响应时间为2．8s；当k值增加到30时，查询的平均响应时间仅仅是0．3s．这对大规模网络上的在线查询来说是非常有意义的．

6 结 论

本文研究了异构信息网络上的可达性查询问题．利用不同类型顶点之间的关系，查询2个顶点间满足路径模式的可达性．提出一种新的索引结构，通过路径模式的分解，预先计算部分路径模式的可达信息．当查询到来时，在路径模式的偏序图上，快速找到索引结构中包含的路径子模式，高效计算查询结果．最后实验验证了本文提出的算法能够在大规模网络上高效响应用户在线查询．异构信息网上的可达性查询问题可以深入挖掘不同类型顶点之间的联系，对于分析和挖掘异构信息网络有重大意义．

［1］Fu Lizhen，Meng Xiaofeng．Reachability indexing for largescale graphs：Studies and forecasts［J］．Journal of Computer Research and Development，2015，52（1）：116 129（in Chinese）（富丽贞，孟小峰．大规模图数据可达性索引技术：现状与展望［J］．计算机研究与发展，2015，52（1）：116 129）

［2］Agrawal R，Borgida A，Jagadish H V．Efficient management of transitive relationships in large data and knowledge bases［C］??Proc of ACM SIGMOD Int Conf on Management of Data．New York：ACM，1989：253 262

［3］Jin R，Xiang Y，Ruan N，et al．3－hop：A high－compression indexing scheme for reachability query［C］??Proc of ACM SIGMOD Int Conf on Management of Data．New York：ACM，2009：813 826

［4］Jin R，Xiang Y，Ruan N，et al．Efficiently answering reachability queries on very large directed graphs［C］??Proc of ACM SIGMOD Int Conf on Management of Data．New York：ACM，2008：595 608

［5］Wang Haixun，He Hao，Yang Jun，et al．Dual labeling：Answering graph reachability queries in constant time［C］?? Proc of the 22nd Int Conf on Data Engineering．Piscataway，NJ：IEEE，2006：75 75

［6］Cheng J，Shang Z，Cheng H，et al．K－reach：Who is in your small world［J］．Proceedings of the VLDB Endowment，2012，5（11）：1292 1303

［7］Cohen E，Halperin E，Kaplan H，et al．Reachability and distance queries via 2－hop labels［J］．SIAM Journal on Computing，2003，32（5）：1338 1355

［8］Wei F．TEDI：Efficient shortest path query answering on graphs［C］??Proc of Int Conf on Management of Data．New York：ACM，2010：99 110

［9］Cheng J，Yu J X．On－Line exact shortest distance query processing［C］??Proc of the 12th Int Conf on Extending Database Technology．New York：ACM，2009：481 492

［10］Xiao Y H，Wu W T，Pei J，et al．Efficiently indexing shortest paths by exploiting symmetry in graphs［C］??Proc of the 12th Int Conf on Extending Database Technology．New York：ACM，2009：493 504

［11］Cheng J，Ke Y P，Chu S，et al．Efficient processing of distance queries in large graphs：A vertex cover approach［C］??Proc of Int Conf on Management of Data．New York：ACM，2012：457 468

［12］Jin R，Hong H，Wang H，et al．Computing label－constraint reachability in graph databases［C］??Proc of ACM SIGMOD Int Conf on Management of Data．New York：ACM，2010：123 134

［13］Jin R，Ruan N，Xiang Y，et al．Path－tree：An efficient reachability indexing scheme for large directed graphs［J］．ACM Trans on Database Systems（TODS），2011，36（1）：7：1 7：44

［14］Xu K，Zou L，Yu J X，et al．Answering label－constraint reachability in large graphs［C］??Proc of ACM Int Conf on Information and Knowledge Management．New York：ACM，2011：1595 1600

［15］Cheng J，Yu J X，Ding B，et al．Fast graph pattern matching［C］??Proc of the 24th Int Conf on Data Engineering．Piscataway，NJ：IEEE，2008：913 922

［16］Tong H，Faloutsos C，Gallagher B，et al．Fast best－effort pattern matching in large attributed graphs［C］??Proc of ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining．New York：ACM，2007：737 746

［17］Zou L，Chen L，Tamer M．Distance－join：Pattern match query in a large graph database［J］．Proceedings of the VLDB Endowment，2009，2（1）：886 897

［18］Sun Y，Han J，Yan X，et al．Pathsim：Meta path－based topk similarity search in heterogeneous information networks［J］．Proceedings of the VLDB Endowment，2011，4（11）：992 1003

［19］Sun Y，Barber R，Gupta M，et al．Co－author relationship prediction in heterogeneous bibliographic networks［C］?? Proc of IEEE Int Conf on Advances in Social Networks Analysis and Mining．Piscataway，NJ：IEEE，2011：121 128

［20］Sun Y，Yu Y，Han J．Ranking－based clustering of heterogeneous information networks with star network schema［C］??Proc of ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining．New York：ACM，2009：797 806

［21］Sun Y，Han J，Zhao P，et al．RankClus：Integrating clustering with ranking for heterogeneous information network analysis［C］??Proc of the 12th Int Conf on Extending Database Technology：Advances in Database Technology．New York：ACM，2009：565 576

［22］Sun Y，Norick B，Han J，et al．Integrating meta－path selection with user－guided object clustering in heterogeneous information networks［C］??Proc of ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining．New York：ACM，2012：1348 1356

［23］Shen W，Han J，Wang J．A probabilistic model for linking named entities in Web text wit heterogeneous information networks［C］??Proc of ACM SIGMOD Int Conf on Management of Data．New York：ACM，2014：1199 1210

Yin Dan，born in 1987．PhD candidate．Her research interests include massive data management and graph database．

Gao Hong，born in 1966．Professor，PhD supervisor．Her research interests include massive data management and wireless sensor networks．

Zou Zhaonian，born in 1979．PhD，lecturer．His research interests include massive data management and graph database．

Li Jianzhong，born in 1950．Professor，PhD supervisor．His research interests include massive data management and wireless sensor networks．

Reachability Query in Heterogeneous Information Networks

Yin Dan，Gao Hong，Zou Zhaonian，and Li Jianzhong
（School of Computer Science and Technology，Harbin Institute of Technology，Harbin150001）

With the size of graph data increasing explosively，the form of graph data is much more complicated．Heterogeneous information networks can be modeled as graphs，which contain multiple types of nodes and multiple types of edges，e．g．，bibliographic database，online shopping website and knowledge graphs．Reachability query in heterogeneous information networks is investigated in this paper．By using different types of relationships between nodes，the reachability of nodes is queried while satisfying specific path schema．This problem is polynomial．However，the time costing can t be tolerant by scanning the big network for answering one query．The existing reachability work can be classified into two categories：K－hop reachability query and label－constraint reachability query．But these techniques can t be used for processing path－based reachability query in heterogeneous information networks．Therefore，in order to respond online queries efficiently，a novel index structure is proposed，which decomposes path schemas and precomputes the reachability of nodes in sub－path schemas．Online query is computed efficiently by decomposing the query path schema and using the reachability of the indexes．A path schema decomposition strategy is developed by searching the partial order graph of path schemas in order to minimize the query time．Experiments on real world and synthetic data demonstrate the effectiveness of algorithms for reachability query in heterogeneous information networks．

heterogeneous information network；query processing；reachability；path schema；index

TP311．1

2015－11－24；

2015－02－28

国家“九七三”重点基础研究发展计划基金项目（2012CB316200）；国家自然科学基金重点项目（61033015）；国家自然科学基金重大项目（61190115，60933001）；国家自然科学基金面上项目（61173023）

This work was supported by the National Basic Research Program of China（973Program）（2012CB316200），the Key Program of the National Natural Science Foundation of China（61033015），the Major Program of the National Natural Science Foundation of China（61190115，60933001），and the General Program of the National Natural Science Foundation of China（61173023）．