基于MapReduce的多元连接优化方法

李甜甜 于 戈 郭朝鹏 宋 杰

1（东北大学计算机科学与工程学院 沈阳 110819）2（东北大学软件学院 沈阳 110819）（litiantian＿neu＠163．com）

基于MapReduce的多元连接优化方法

李甜甜1于 戈1郭朝鹏2宋 杰2

1（东北大学计算机科学与工程学院 沈阳 110819）2（东北大学软件学院 沈阳 110819）（litiantian＿neu＠163．com）

多元连接是数据分析最常用的操作之一，MapReduce是广泛用于大规模数据分析处理的编程模型，它给多元连接优化带来新的挑战：传统的优化方法不能简单地适用到MapReduce中；MapReduce连接执行算法尚存优化空间．针对前者，考虑到I?O代价是连接运算的主要代价，首先以降低I?O代价为目标提出一种启发式算法确定多元连接执行顺序，并在此基础上进一步优化，最后针对MapReduce设计一种并行执行策略提高多元连接的整体性能．针对后者，考虑到负载均衡能够有效减少MapReduce的“木桶效应”，通过任务公平分配算法提高连接内部的并行度，并在此基础上给出Reduce任务个数的确定方法．最后，通过实验验证本文提出的执行计划确定方法以及负载均衡算法的优化效果．该研究对大数据环境下MapReduce多元连接的应用具有指导意义，可以优化如OLAP分析中的星型连接、社交网络中社团发现的链式连接等应用的性能．

多元连接；执行计划；I?O代价；性能优化；MapReduce编程模型；负载均衡

连接运算根据连接条件把2个或多个关系中的记录组合为一个结果数据集，包含连接运算的查询简称为连接查询．连接查询在数据分析中很常见，TPC－H提供的22个查询用例中有16个涉及到此类查询［1］．当一个连接查询涉及n个关系时，称为n元连接；当n＞2时，称为多元连接，多元连接是数据分析中最常用的操作之一．此外，在当今的大数据环境下，MapReduce［2］编程模型被广泛用于大规模数据集的分析处理．目前，MapReduce中数据分析的优化工作包括索引、数据布局、查询优化、迭代处理、公平负载分配以及交互式处理等方面［3］．基于此，我们分析MapReduce给多元连接的优化带来的新挑战．

首先，多元连接查询依赖良好的执行计划．传统的执行计划确定方法［4］不满足MapReduce特性，无法通过简单的适应性更改应用到现有的优化中．另外，现有基于MapReduce的执行计划确定方法［5－6］复杂度较高，应用范围受限．因此，亟需提出一种新的满足MapReduce特性且复杂度较低的执行计划确定方法．此外，我们还注意到，无论是传统研究还是现有研究，其执行计划都只确定了连接的执行顺序，并未考虑无依赖关系的连接操作间的并行执行策略．

其次，良好的执行计划固然重要，对执行框架的优化同样可以有效地提高多元连接的性能，这一点在分布式环境中尤为重要．一种公平的并行任务负载分配方法可以有效地减少MapReduce中的“木桶效应”，从而提高连接操作内部的并行度．然而，就我们所知，目前没有针对连接运算的MapReduce负载均衡方法，且现有的通用方法［7－9］仅考虑了任务的输入代价，不适用于连接运算，因为它的输出代价也不可忽略．

本文研究MapReduce环境下多元连接的优化方法，基于上述分析提出以下问题：1）多元连接执行计划的解空间很大，短时间内很难找到最优解，那么能否通过某个复杂度较小的算法快速找到一个近似最优解；2）连接运算属于I?O密集型运算，I?O为主要代价，那么能否针对MapReduce特性提出I?O代价模型，并选择代价最小的执行计划；3）连接顺序确定后，不存在依赖关系的连接操作可以并行执行，那么当存在多个满足并行执行的连接操作时该如何选择；4）执行框架的优化中，负载均衡能够有效地减少“短板效应”，那么此处的连接负载又该如何定义．这些问题的求解存在一定程度的挑战，就我们目前所知，尚未发现能够完全解决上述问题的研究工作．

本文首先通过分析多元连接执行计划解空间的缩减方法、MapReduce连接算法的I?O代价模型、Replicated Join①的优劣以及MapReduce作业的并行执行特性，最终确定了执行计划的优化方法；接着，结合MapReduce框架分析连接运算的特性，提出负载均衡模型及其对应的均衡算法，并在此基础上提出Reduce任务个数的确定方法．大量实验验证了本文提出的优化方法的有效性．

1 相关工作

现有多元连接的优化研究可归为以下3类：执行计划的优化、连接算法的优化和执行框架的优化．

对于第1类研究，文献［4］将n元连接拆分为n－1个2元连接，每个2元连接对应一个MapReduce作业（后文如不特殊指明，作业均为MapReduce作业），然而该方法针对的是传统的多处理器计算环境，不适用于MapReduce，且该方法在n较大时会导致较高的作业初始化代价以及中间结果的存储代价．文献［10］针对链式连接提出使用平衡二叉树的方式来执行多元连接，但其并未给出平衡二叉树的构建规则．文献［11］在一个作业中完成所有的连接运算，然而该方法在n较大时会因为数据需要传输

①Replicated Join：在一个MRJ中执行多个连接操作．此时，同一个Key－Value对需要被复制到多个Reducer上，因此称为Replicated Join．该算法牺牲部分网络I?O代价来换取MRJ的初始化以及HDFS读写代价．到多个Reducer而导致较高的网络I?O代价．文献［5－6］将n元连接划分为若干个组，每组涉及若干个关系并由一个作业完成，而后采用Replicated Join连接所有组生成的中间结果，然而该方法因为要穷举所有可能的m（m＜n）元连接作为候选集而导致算法复杂度较高，从而使其应用范围较窄．此外，上述所有研究确定的执行计划都只确定了连接的执行顺序，并未考虑无依赖关系的连接操作间的并行执行策略．

本文首先基于MapReduce特性提出多元连接顺序的确定方法，该方法复杂度较低且能够很好地均衡中间结果的存储代价与网络传输代价．确定连接顺序后，本文还给出一种算法来确定无依赖关系的连接操作间的并行执行顺序，该算法通过对节点资源的充分利用来提高多元连接的执行效率．

对于第2类研究，文献［12］针对theta－join提出一种随机算法1－Bucket－Theta以及它的一个扩展算法M－Bucket；文献［13］对文献［12］中提出的算法进行下界分析，并通过聚类方法提高了M－Bucket算法的效率．文献［14－15］总结现有实现算法为Map Join，Reduce Join，Semi Join等，这些算法分别适用于不同的查询场景，如Map Join仅适用于数据量较小的关系能够装入内存的查询．MapReduce连接算法的优化研究相对比较成熟，不在本文的研究范围之内．因此，不失一般性，本文采用没有任何约束条件的通用的Reduce Join作为研究对象．

连接运算的执行效率依赖于实现算法和运行环境，由此衍生出第3类研究．文献［16］基于MapReduce提出一个改进的执行框架Map－Reduce－Merge，新添加的Merge阶段为Reduce Join的执行节省了一次作业．文献［17］对MapReduce框架进行修改，允许不同操作间的数据管道式传输，支持在线聚集以及持续查询，然而改进后的框架使得失效恢复（fail recovery）机制变得非常复杂，且对于批处理性能的提高也很不明显．文献［7－9］给出了通用的MapReduce负载均衡方法，但他们都只考虑了任务的输入代价，不适用于连接运算，因为它的输出代价也不可忽略．本文提出的MapReduce负载均衡方法着重考虑连接任务的负载特性，与传统的负载均衡方法有所不同．具体来讲，本文提出的负载均衡方法基于的Reduce Join的Map阶段仅负责将参与连接的数据表中的记录解析成Key－Value对（此时I?O操作很少），并通过Shuffle阶段传输到对应的Reduce任务中，而真正的连接操作是在Reduce阶段中完成的（此时会产生大量I?O操作）．考虑到I?O代价是影响连接查询的主要因素，我们对产生大量I?O操作的Reduce阶段进行读写分析，综合考虑Reduce任务的输入和输出代价及其对应的读写权重，最终基于这一综合代价给出了Reduce任务的负载均衡方法．文献［18］中实现的负载均衡是通过均衡数据块实现的，本文与其有本质上的区别．

2 连接执行计划

多元连接执行计划的解空间很大，短时间内很难找到最优解．本节首先通过查询树模型确定解的一个子空间，而后通过复杂度较小的启发式算法从中找到一个近似最优解，并在此基础上做进一步的优化以均衡中间结果的存储代价与网络传输代价．最后，根据MapReduce框架特性给出一种算法来确定无依赖关系的连接操作间的并行执行顺序，该算法通过对节点资源的充分利用来提高多元连接的效率．

2．1 查询树模型

多元连接可以用一个查询图G＝（V，E）来表示［46］，其中V是节点的集合，每个节点代表一个关系（记为Ri），E是边的集合，每条边?Ri，Rj?连接2个之间存在连接属性（A，B，C等）的关系，如图1所示．图1（a）所示的查询图包含6个关系，为6元连接；同理，图1（b）所示的查询图为8元连接．

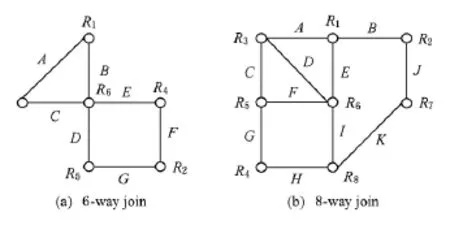
Fig．1 Example queries of multi－way join．图1 多元连接查询示例

多元连接执行计划的最优解确定是个P完全问题［6］，传统优化方法通常采用查询树模型限定解的一个子空间，并设计算法从中获取一个最优解．如图2所示，主流的查询树模型有Left－deep Tree，Right－deep Tree，Zigzag Tree，Bushy Tree［19］四种，其中前3种为顺序执行，最后1种为并行执行．很多研究工作［4－5］显示，并行执行的Bushy Tree更适用于分布式环境．从图2也可以看出，只有基于Bushy Tree确定的连接顺序中不同连接操作间不是完全的依赖关系，是可以并行的．因此，本文选取Bushy Tree作为MapReduce多元连接的查询树模型．

Fig．2 Query trees．图2 查询树模型

2．2 查询树模型

一个n元连接的执行方式有2种：1）将其拆分为n－1个2元连接分别执行，每个2元连接对应一个作业；2）在一个作业中执行所有连接操作．然而，当n较大时，第1种执行方式的作业初始化代价以及中间结果的存储代价也随之增大，第2种执行方式也因为数据的多次传输而产生较大的网络代价．为解决该问题，本文首先基于Bushy Tree初步确定多元连接的执行顺序，而后根据是否受益将部分2元连接合并成多元连接．

1）基于I?O代价的连接顺序确定方法

通过Bushy Tree确定多元连接的执行顺序首先需要给出树的构建规则．考虑到连接运算属于I?O密集型计算，连接代价以I?O代价为主，本文针对MapReduce特性给出连接运算的I?O代价模型，并选择I?O代价最小的连接顺序．

正如第1节中的描述，本文选择Reduce Join作为连接算法，下面以2元连接为例对其进行简单介绍．Reduce Join由Map阶段和Reduce阶段组成．Map阶段主要完成如下操作：①Map任务读取（通常为本地读）参与连接的2个关系；②以连接属性为键、记录为值，按键排序后输出键值对到本地磁盘；③将中间结果通过网络传输给Reduce任务．Reduce阶段主要完成如下操作：①接收来自Map任务的键值对并按键排序；②执行连接操作，并将结果写入分布式文件系统（HDFS）．

基于该分析，我们给出关系Ri和Rj进行Reduce Join的I?O代价计算方法，见式（1）：

其中，C1，C2，C3分别为本地、网络和HDFS的I?O代价权重，三者均与系统硬件相关（其中C3还与HDFS的副本个数设置有关），其值均可事先通过文件读写实验测出（在本文的实验环境中，副本个数为3，通过实验测得3个参数的值分别为C1＝3．67s?GB，C2＝8．93s?GB，C3＝13．37s?GB，三者之间的比值为1：2．4：3．6）；｜Ri｜代表关系的基数．另外，Map阶段操作②首先需要溢出写文件，而后读取并排序输出，因此共需3次读写操作；Reduce阶段的操作①使用内存和磁盘进行混合式排序，因此我们用参数λ表示该混洗比例，其值可通过经验设定．

通过Bushy Tree确定连接顺序时，我们每次从查询图G＝（V，E）中选择I?O代价最小的连接操作执行，而后更新图G及其对应的关系的特征参数，直到执行完所有连接运算（见算法1）．算法1的复杂度为O（log（｜V｜｜E｜）），小于文献［5－6］的复杂度O（log（｜V｜2｜E｜））．

算法1．PMC算法．?＊基于MC（minimal cost）的执行计划（plan）确定算法＊?

输入：G＝（V，E），query profile；?＊包括关系的基数、连接属性的基数等相关参数＊?

输出：Bushy Tree．

PMC算法中计算最小代价时，｜Ri｜和｜Rj｜均已知，｜RiRj｜未知，需要我们计算．目前关于｜RiRj｜的计算方法通常假设Ri和Rj在连接属性A上均匀分布［4，9］，具体计算方法见式（2）：

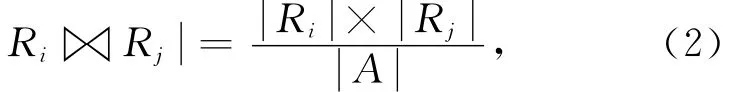
其中，｜A｜为连接属性的基数．然而，事实上Ri和Rj通常不满足均匀分布这一假设，因此在实际应用中，我们应该考虑数据倾斜因素．设Fi和Fj为A在Ri和Rj中出现的频数分布，则定义倾斜度如下：

定义1．倾斜度．定义倾斜度δ为频数分布Fi和Fj偏离均匀分布的程度，表达式见式（3）：

在实际计算中，倾斜度可以通过采样获取．有了倾斜度，｜RiRj｜的计算方法见式（4）：

因为

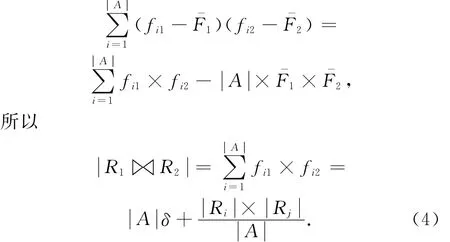
考虑倾斜度因素计算出的｜RiRj｜更精确，同时基于最小代价的PMC算法确定的连接顺序也更优．

2）基于Replicated Join的优化

通过Bushy Tree确定的执行顺序仅包含2元连接，这样的执行计划会导致较高的作业初始化代价和中间结果的存储代价．考虑到算法1在复杂度上的优越性，我们保留由它确定的执行顺序，并在此基础上做进一步的优化．

解决上述问题的直观想法为减少作业个数，也即增加每个作业执行的连接操作个数．Replicated Join满足该需求，但该算法中同一个键值对需要被复制到多个Reduce任务上，网络代价较高．为此，本文分别计算查询图采用Replicated Join以及采用多个2元连接这2种执行方法的I?O代价，定义“受益（benefit）”为二者的代价差．当受益为正时，合并这些2元连接，如图3所示．2元连接的I?O代价见式（1），下面给出Replicated Join的I?O代价计算方法．

设查询图G＝（V，E），关系集合V＝｛R1，R2，…，Rn｝，E关联的连接属性集合为E－，Ri关联的连接属性集合为E－i，Replicated Join的I?O代价计算见式（5）：

Fig．3 Optimization based on replicated join．图3 基于Replicated Join的优化

基于Replicated Join的优化需要对PMC算法确定的Bushy Tree进行遍历，以合并所有可能的2元连接．然而，这样做的代价很高，本文考虑到对无依赖关系的连接操作执行Replicated Join明显会导致较高的网络I?O代价，因此仅判定具有依赖关系的连接操作（也即图3（a）中只能顺序执行的子树）．另外，如果一个顺序执行的子树进行Replicated Join时受益为负，那么包含该子树的顺序执行子树的受益也为负．通过以上方法能够大大降低树的遍历代价．基于Replicated Join的优化算法见算法2．

OPTB的算法复杂度小于PMC算法确定的Bushy Tree中所有最大顺序执行子树的高度之和．又考虑到顺序执行子树的最大高度为n－1，故OPTB的算法复杂度为O（n）．

2．3 并行执行顺序

很多关于多元连接执行计划的优化研究［4－6］都只确定了连接的执行顺序，并未考虑MapReduce环境下无依赖关系的连接操作间的并行执行策略．

若图3（b）为2．2节中最终优化的多元连接顺序，那么连接操作R2R7，R4R8，R3R5R6之间无依赖关系，可以并行执行．下面结合MapReduce特性对并行执行的优势进行分析．

MapReduce集群中每个节点最多可执行的Map任务个数是预设的，因此最多可并行执行的Map任务数也是确定的．对于连接运算，Reduce Join中的Map任务负责将关系中的元组按照连接属性值进行分区，其执行时间仅取决于处理数据量．又因为每个Map任务处理一个固定大小的分片，我们可以认为同时分配的Map任务同时结束．设MapReduce每次最多可并行的Map任务个数为M，M个任务的并行执行称为一轮［2，20－21］．若每轮Map任务的执行时间为T，作业Ji需要的Map任务个数Mi＝ai×M＋bi，其中ai，bi∈NN，bi∈［0，M），那么可以认为Ji的执行时间为（ai＋ bi?M ）T．若作业Jj需要的Map任务个数Mj＝aj×M＋bj，那么当bi＋bj≤M时，2个作业的并行执行时间为（ai＋aj＋1）T，而串行执行时间为（ai＋aj＋2）T，此时并行执行可节省T时间；当bi＋bj＞M时，并行执行时间和串行执行时间同为（ai＋aj＋2）T．综上，当bi＋bj≤M时，作业Ji和Jj并行执行的效率高于串行．

当有多个作业满足这一条件时，我们选取bi＋bj最大的2个作业并行执行，从而充分利用计算资源．下面给出具体的算法实现：

2．4 小 结

通过2．2节和2．3节给出的优化算法，我们最终动态确定多元连接的执行计划．图4以流程图的方式描述了执行计划的优化步骤．

Fig．4 Optimization flow of the execution plan．图4 执行计划优化流图

给定查询图G，首先通过PMC算法初步确定Bushy Tree，而后分别通过算法OPTB和PEE进行优化，直到更新后的树中叶子节点的个数小于3．

3 负载均衡

良好的执行计划固然重要，但对执行框架的优化同样可以有效地提高多元连接的执行效率，这一点在分布式环境中尤为重要．一种公平的并行任务负载分配方法可以有效地减少MapReduce中的“短板效应”，从而提高连接操作内部的并行度．

连接运算的MapReduce实现算法有很多，分别适用于不同的查询场景．不失一般性，本文选择没有任何约束条件的Reduce Join作为连接执行算法．该算法包括Map和Reduce 2个阶段，Map阶段只负责将关系中的元组按照连接属性值进行分区以输出到不同的Reduce任务，运算完全相同，因此Map任务的负载完全取决于处理数据量．又因为MapReduce中每个Map任务只负责处理一个数据分片（split，默认64MB），所以Map阶段各个Map任务是负载均衡的．很多研究工作也都作出Map任务均衡的假设，如文献［6，22］．因此，本文仅研究连接运算的Reduce任务负载均衡．

Reduce Join算法在Reduce阶段执行连接运算，连接属性值的不均匀分布将会导致由默认Hash分区函数确定的Reduce任务负载不均衡．为提高Reduce任务间的并行度，本节给出一种针对连接运算的负载均衡优化方法．

3．1 负载均衡模型

设R1和R2为参与连接的2个关系，连接属性值的集合记为A，A在R1和R2中的频数分布分别为F1和F2．在计算Reduce任务的负载之前，我们先给出连接属性值a∈A的负载贡献定义如下：

定义2．负载贡献．连接属性值a∈A的负载贡献（LCa）是指执行该连接操作的代价，见式（6）：

LCa＝ω1（f1a＋f2a）＋ω2（f1a×f2a），（6）其中，f1a和f2a分别为R1和R2中连接属性值为a的元组个数；ω1和ω2为Reduce任务输入数据和输出数据的处理代价权重，输入数据为网络I?O，输出数据写到HDFS上，二者的比值是由运行多元连接的分布式集群系统决定的．此处，我们认为连接运算代价中I?O占主导地位，CPU处理代价可以忽略，文献［5－6］中也有同样结论．文献［8］给出的当前最好的负载均衡方法中采用的代价模型仅考虑输入数据对Reduce任务负载的影响，而事实上对于连接运算输出数据的代价不容忽略．

通过对MapReduce运行机制的分析可知，Reduce任务的负载取决于分区函数．分区函数将连接属性值划分成若干个组，每组对应一个Reduce任务．设分区函数将连接属性值的集合A划分为A1，A2，…，AR一共R个组，那么组Ai的处理代价

第i个Reduce任务的负载Load（Ri）＝Load（Ai），Reduce任务负载均衡这一目标可以等价表示如下：

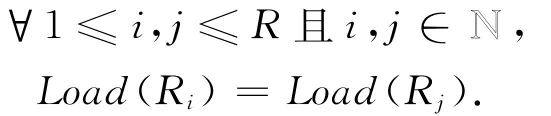
负载均衡模型中最关键的是获取连接属性A在R1和R2中的频数分布F1和F2．获取这2个分布，最精确的方法是对不同键值进行频数统计［23］，但当键值个数很多时，会耗费大量存储，且在汇总各个Map任务的统计信息时还会带来很高的网络传输代价．针对该问题，文献［5，7－9］对键值进行Hash从而降低统计信息的规模．然而，文献［9］在Map任务执行的同时对频数信息进行统计，这样会导致第2轮Map任务无法执行，还会造成数据到Reduce的传输延迟，因为必须等到根据频数信息确定Partition函数后才能进行传输．文献［5，7－8］则单独开启一个作业进行频数统计，避免了上述问题．基于以上分析，本文可以采用类似的方法获取连接属性值的频数信息，并据此确定Reduce任务的个数以及Partition函数．

3．2 负载均衡算法

文献［6］指出Reduce任务的负载均衡是一个NP难问题，不能够在多项式时间内获取最优解，因此我们仅专注于寻找尽可能接近最优解的近似解．由于连接属性值的不可分割性，拥有相同连接属性值的键值对必须发送到同一Reduce任务节点进行连接运算，Reduce任务的负载均衡问题可以转换成尽可能降低Reduce任务的最大负载max｛Load（Ri）｝．

理想情况下，所有Reduce任务的负载完全相同，此时max｛Load（Ri）｝＝Avg｛Load（Ri）｝．然而，这种情况不总发生，本文给出一种朴素的均衡算法来获取近似解．该算法首先对A中所有连接属性值的负载贡献值按降序排序，然后每次将连接属性值为a的键值对分配给当前负载最小的Reduce任务（详见算法4）．

为评估算法4，我们将由该算法获取的Reduce任务负载最大值Lmax与最优算法获取的最大值L＊max进行对比，并得出Lmax的上界如下：Lmax≤1．5L＊max．

本文给出的负载均衡方法是以等值连接为例进行描述的，它还适用于其他连接，也可以扩展到连接以外的其他类型作业．例如，进行近似连接时，只需将连接属性值a（键值对中的键）替换为一个满足近似条件（如｜a1－a2｜≤δ）的2元组?a1，a2?，并将负载贡献值的计算公式中f1a和f2a分别替换为R1中连接属性值为a1的元组个数以及R2中连接属性值为a2的元组个数．执行Replicated Join时，键值对中的键将会变成多个连接属性构成的多元组．对于连接以外的其他作业，我们可以将Reduce任务输入数据的处理代价函数（频数的加和）以及输出数据的处理代价函数（频数的乘积）进行适应性的更改．

3．3 Reduce任务个数的确定

现有通用的Reduce端负载均衡的方法［7－9］均未考虑Reduce任务个数的确定方法，本文根据获取的键值频数统计信息给出一种简单的确定规则．

设Map任务的输出中不同键值的个数为k，所有键值的负载贡献和为Sum，其中键值的最大负载贡献为LCmax，Reduce任务个数为R，通过优化算法获取的Reduce任务最大负载为Lmax．当LCmax≥Sum?R时，也即R≥Sum?LCmax时，Lmax的取值不再下降，始终为LCmax，这意味着作业的性能不再提高，而它的资源消耗却随着R的增加而增大．因此，有必要找到R的一个临界值使得连接的执行效率最高．另外，考虑到Lmax的取值还与Sum有关，本文给出均衡算法的度量函数g（Lmax，R）的表达式如下：

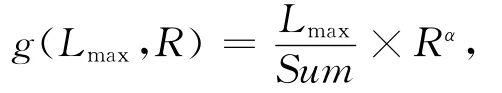
其中，α是性能与能耗之间的权重比，度量值越小，均衡效果越好．函数g（Lmax，R）应该存在一个极小值点R0，使得在该点处性能与资源消耗达到一个很好的折中，且该值有可能比Sum?LCmax小．4．2节中通过大量实验得出，当α＝0．05时，函数g（Lmax，R）的极小值点正好就是Lmax不再下降的临界值．

另外，考虑到不同键值的个数可能会很大，这将导致频数统计信息不能存入内存，针对该问题，我们可以采用文献［8］中提出的optimal sketch packing算法，该方法通过Hash函数将键值（这里是负载贡献值）进行哈希后再进行均衡分配，从而降低键的规模，节省统计信息占用的内存．本质上，该方法是牺牲精确度来降低统计信息的存储空间．

4 实验与范例分析

本节设计实验对提出的连接执行计划优化方法以及连接负载均衡方法进行验证和分析．其中，4．1节中的实验是依托图1中给出的查询图生成的虚拟数据表进行多元连接查询设计的，该实验能够很好地验证本文提出的执行计划的优化效果；4．2节中的实验则是依托TPC－H数据集中提供的逻辑数据表进行设计的，本文通过控制其数据的生成方式来设计实验以验证文中提出的连接负载均衡方法．实验的具体设置在4．1节和4．2节中均有对应的详细描述．

4．1 执行计划的优化效果分析

以图1中查询图为例对本文提出的执行计划优化方法进行效果分析，相应的特征参数见表1和表2．

Table 1 Cardinalities of the Relations in Fig．1（a）表1 图1（a）对应的关系特征参数

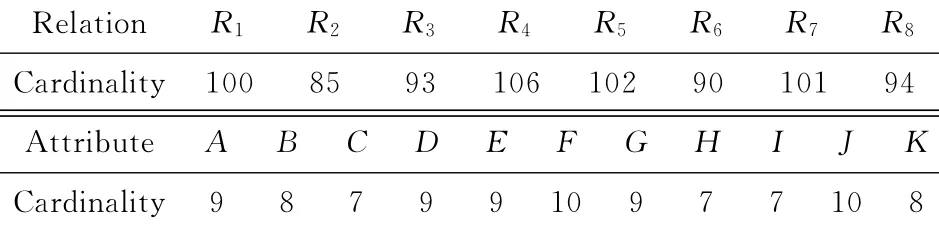
Table 2 Cardinalities of the Relations in Fig．1（b）表2 图1（b）对应的关系特征参数

首先，为了验证本文提出的连接顺序确定PMC算法的优化效果，本文将其与最优解（可用分支限定法获取）进行对比．图5中，POPT代表最优解，从图5可以看出PMC的代价比最优解稍高，二者的比值分别为1．003和1．034．由此可见，PMC算法能够确定一个很好的连接顺序，从而降低连接的I?O代价．

接着，我们分析了2种查询图下算法OPTB和PEE的优化效果．从表3可以看出，OPTB算法能够找出可以合并为多元连接的2元连接，一定程度上降低了I?O代价；PEE算法能够找出最大限度使用集群计算资源的可并行连接操作，从而节省多元连接的整体运行时间．

Fig．5 I?O cost comparison of PMCand POPT．图5 PMC算法与POPT的I?O代价对比

Table 3 Optimization Results of Algorithms OPTBand PEE表3 算法OPTB和PEE的优化效果

4．2 负载均衡方法验证

文献［5，7－9］中均提到采用模拟实验验证其提出的负载均衡方法，假设键值服从Zipf分布．不失一般性，本文也采用该方法来验证第3节中针对连接运算设计的负载均衡方法．以等值2元连接为例，假设参与连接的2个关系表R1和R2服从相同的Zipf分布，数据条数分别为｜R1｜和｜R2｜，不同连接属性值的个数为k，则R1和R2中第i个最频繁出现的连接属性值的出现概率pi＝1?（iz×Hk），其中z代表数据的倾斜度，Hk是调和系数，那么第i个连接属性值的负载贡献值计算如下：

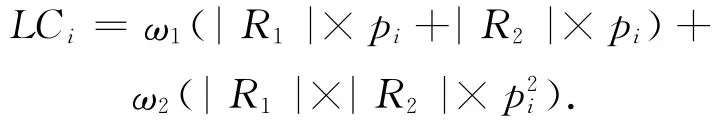
依托TPC－H数据集中提供的逻辑数据表，我们设计具体的测试用例为：｜R1｜＝109，｜R2｜＝2×109，k＝3×104，3×105，3×106，z的取值范围为［0，1］．这里需要指出的是，z仅代表关系R1和R2中连接属性值的倾斜程度，并不代表负载贡献值集合的倾斜度（记为δ），但δ与z值是成正相关的，且比z大．

首先，我们对比不同因素下负载均衡算法的效果，采用IR（imbalance ratio）来度量，它是所有Reduce任务中的最大负载（Lmax）与平均负载（Avg＝Sum?R）之间的比值．从图6可以看出，IR的影响因素有δ（受z影响），k和R，与δ和R成正相关，与k成负相关．从图6我们还可以看出，IR的值早在z＝0．5，R＝64时已经超过1．5，这是因为IR是Lmax与Avg之间的比值，而通过最优负载均衡算法获取的L＊max通常会因为δ较大而远大于Avg．例如，当一个键的频数占总频数的80%时，因为键的不可分割性，Lmax和L＊max会远大于Avg．

其次，为了验证本文设计的负载均衡算法的有效性，我们将其得到的最大负载值与默认Hash函数得到的最大负载值进行对比．从图7可以看出，在3种倾斜度、3种Reduce个数下，我们的算法均比默认Hash的好．从图7（a）可以看出，随着Reduce个数的增加，负载均衡算法的优势越来越明显；而在图7（b）和图7（c）中，Reduce个数为100和1 000时，均衡算法得到的最大负载值均未发生变化，这是因为此时数据太过倾斜而产生了“二八现象”，图7（b）和图7（c）对应的最大负载值分别在Reduce个数大于95以及16后不再发生变化（从图8中可以看出），这也验证了我们在3．3节中的理论分析．另外，在图7（b）和图7（c）中，虽然默认Hash得到的最大负载值依然随着Reduce个数的增加而降低，但该值由于数据倾斜以及键值不可分割等原因而不会低于均衡算法得到的值．

最后，为了验证3．3节中提出的Reduce任务个数的确定方法，我们分析了正规化后的最大负载Lmax与负载均衡算法的评估函数g（Lmax，R）随Reduce任务个数R的变化情况．通过大量实验，我们发现当函数g（Lmax，R）中的α＝0．05时，它的极小值点正好就是Lmax不再下降的临界值R0．另外，在实验过程中，我们发现z值越大，临界值R0的下降趋势越不明显，因此，为直观起见，本文选取了其中5个具有代表性的z值进行展示．从图8（a）可以看出，随着R的增长，Lmax不断减小，最终趋向平稳值，图中5个z值对应的临界R值分别为974，95，16，6，4，这与我们通过均衡算法度量函数g（Lmax，R）得到的极小值点是完全吻合的（见图8（b））．

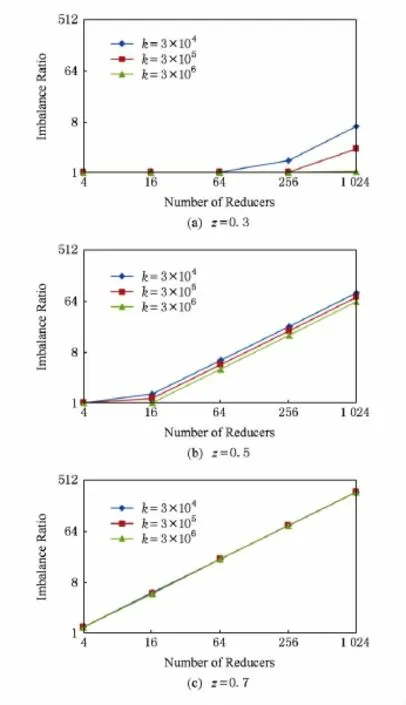
Fig．6 Imbalance ratios of the load balancing algorithm under different skew degrees．图6 不同倾斜度下负载均衡算法的IR比较

Fig．7 Max load comparison between the load balancing algorithm and the default Hash under 3million keys．图7 k＝3×106时不同倾斜度下负载均衡算法与默认Hash的最大负载对比

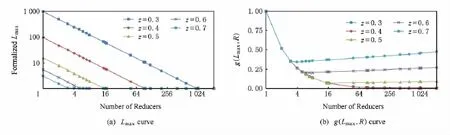
Fig．8 Relationships between the formalized Lmax，g（Lmax，R）and Runder 3million keys．图8 k＝3×106时正规化的最大负载Lmax以及函数g（Lmax，R）随R的变化曲线

5 总 结

本文基于MapReduce研究多元连接的优化方法，主要从以下2部分展开研究：连接的执行计划和连接的负载均衡．

针对前者，本文首先分析现有主流的查询树模型，确定适合本文研究环境的Bushy Tree；随后通过白盒分析给出MapReduce连接算法的I?O代价模型，并选择I?O代价最小的连接顺序作为初步的执行计划；接着对执行计划做进一步的优化，根据是否受益将查询树中的2元连接合并成Replicated Join，以降低多个作业引起的中间结果代价；最后结合MapReduce特性提出一种作业并行执行算法，以提高集群资源的使用率．

针对后者，本文首先分析连接运算的特性，给出连接负载的定义以及负载均衡目标；接着给出具体的均衡算法，并证明该算法的上界；最后在实验中分析Reduce任务个数的确定与性能之间的关系．

实验证明，本文提出的连接执行计划以及负载均衡的优化算法是有效的．本研究对大数据环境下MapReduce多元连接的应用具有指导意义，可以优化如OLAP分析中的星型连接，社交网络中社团发现的链式连接等应用的性能．

［1］Han Xixian，Yang Donghua，Li Jianzhong．Approximate join aggregate on massive data［J］．Chinese Journal of Computers，2010，33（10）：1919 1933（in Chinese）（韩希先，杨东华，李建中．海量数据上的近似连接聚集操作［J］．计算机学报，2010，33（10）：1919 1933）

［2］Dean J，Ghemawat S．MapReduce：Simplified data processing on large clusters［J］．Communications of the ACM，2008，51（1）：107 113

［3］Doulkeridis C，Norvag K．A survey of large－scale analytical query processing in MapReduce［J］．The VLDB Journal，2013，23（3）：355 380

［4］Chen M S，Yu P S，Wu K．Optimization of parallel execution for multi－join queries［J］．IEEE Trans on Knowledge and Data Engineering，1996，8（3）：416 428

［5］Wu S，Li F，Mehrotra S，et al．Query optimization for massively parallel data processing［C］??Proc of the 2nd ACM Symp on Cloud Computing．New York：ACM，2011：1 13

［6］Zhang X F，Chen L，Wang M．Efficient multi－way theta－join processing using MapReduce［J］．Proceedings of the VLDB Endowment，2012，5（11）：1184 1195

［7］Gufler B，Augsten N，Reiser A，et al．Load balancing in MapReduce based on scalable cardinality estimates［C］??Proc of the Int Conf on Data Engineering．Piscataway，NJ：IEEE，2012：522 533

［8］Yan W，Xue Y，Malin B．Scalable and robust key group size estimation for reducer load balancing in MapReduce［C］?? Proc of the IEEE Int Conf on Big Data．Piscataway，NJ：IEEE，2013：156 162

［9］Gufler B，Augsten N，Reiser A，et al．Handling data skew in MapReduce［C］??Proc of the 1st Int Conf on Cloud Computing and Services Science．Boca Raton，Florida：CRC Press，2011：574 583

［10］Zhou M Q，Zhang R，Zeng D D，et al．Join optimization in the MapReduce environment for column－wise data store［C］??Proc of the 6th Int Conf on Semantics Knowledge and Grid．Piscataway，NJ：IEEE，2010：97 104

［11］Afrati F N，Ullman J D．Optimizing multiway joins in a Map－Reduce environment［J］．IEEE Trans on Knowledge and Data Engineering，2011，23（9）：1282 1298

［12］Okcan A，Riedewald M．Processing theta－joins using MapReduce［C］??Proc of the ACM SIGMOD Int Conf on Management of Data Athens．New York：ACM，2011：949 960

［13］Koumarelas I K，Naskos A，Gounaris A．Binary theta－joins using MapReduce：Efficiency analysis and improvements［C］??Proc of the Workshops of the EDBT ICDT 2014Joint Conf．Boca Raton，Florida：CRC Press，2014：6 9

［14］Blanas S，Patel J M，Ercegovac V，et al．A comparison of join algorithms for log processing in MapReduce［C］??Proc of the ACM SIGMOD Int Conf on Management of Data．New York：ACM，2010：975 986

［15］Luo G，Dong L．Adaptive join plan generation in Hadoop，NC27705［R］．Durham，NC：Duke University，2010

［16］Yang H，Dasdan A，Hsiao R，et al．Map－reduce－merge：Simplified relational data processing on large clusters［C］?? Proc of the ACM SIGMOD Int Conf on Management of Data．New York：ACM，2007：1029 1040

［17］Condie T，Conway N，Alvaro P，et al．Online aggregation and continuous query support in MapReduce［C］??Proc of the ACM SIGMOD Int Conf on Management of Data．New York：ACM，2010：1115 1118

［18］Ding Youwei，Qin Xiaolin，Liu Liang，et al．An energy efficient algorithm for big data processing in heterogeneous cluster［J］．Journal of Computer Research and Development，2015，52（2）：377 390（in Chinese）（丁有伟，秦小麟，刘亮，等．一种异构集群中能量高效的大数据处理算法［J］．计算机研究与发展，2015，52（2）：377 390）

［19］Aljanaby A，Abuelrub E，Odeh M．A survey of distributed query optimization［J］．Int Arab Journal of Information Technology，2005，2（1）：48 57

［20］Agrawal P，Kifer D，Olston C．Scheduling shared scans of large data files［J］．Proceedings of the VLDB Endowment，2008，1（1）：958 969

［21］Li F，Ooi B C，Ozsu M T，et al．Distributed data management using MapReduce［J］．ACM Computing Surveys，2014，46（3）：31：1 42

［22］Nykiel T，Potamias M，Mishra C，et al．MRShare：Sharing across multiple queries in MapReduce［J］．Proceedings of the VLDB Endowment，2010，3（1）：494 505

［23］Ibrahim S，Jin H，Lu L，et al．LEEN：Locality?fairnessaware key partitioning for MapReduce in the cloud［C］??Proc of the 2nd IEEE Int Conf on Cloud Computing Technology and Science．Piscataway，NJ：IEEE，2010：17 24 Li Tiantian，born in 1989．PhD candidate．Student member of China Computer Federation．Her main research interests include energy efficient computing，and data intensive computing．

Yu Ge，born in 1962．Professor and PhD supervisor in Northeastern University．His main research interests include database theory and data flow．

Guo Chaopeng，born in 1990．Master．His main research interests include iterative computing，and data intensive computing．

Song Jie，born in 1980．PhD and associate professor in Northeastern University．His main research interests include cloud computing，data intensive computing and big data．

Multi－Way Join Optimization Approach Based on MapReduce

Li Tiantian1，Yu Ge1，Guo Chaopeng2，and Song Jie21（College of Computer Science and Engineering，Northeastern University，Shenyang110819）2（Software College，Northeastern University，Shenyang110819）

Multi－way join is one of the most common data analysis operations，and MapReduce programming model that has been widely used to process large scale data sets has brought new challenges to multi－way join optimization．Traditional optimization approaches cannot be simply adapted to fit MapReduce feature，so there is still optimization room for MapReduce join algorithm．As to the former，we think I?O is the main cost of join．This paper first proposes an I?O cost based heuristic algorithm to initially determine a join sequence，and conducts further optimization．After the optimization，we also design a parallel execution algorithm to improve the whole performance of multiway join．As to the latter，we think load balancing can effectively decrease the“buckets effect”of MapReduce．This paper proposes a fair task load allocation algorithm to improve the intra－join parallelism，and also analyzes the method to decide the appropriate number of Reduce tasks．Experiments verify the effectiveness of the proposed optimization approaches．This study contributes to multi－way join applications in big data environment，such as the star－join in OLAP and the chainjoin in social network．

multi－way join；execution plan；I?O cost；performance optimization；MapReduce programming model；load balancing

TP393

2014－11－24；

2015－03－04

国家自然科学基金重大项目（61433008）；国家自然科学基金青年基金项目（61202088）；国家博士后科学基金面上项目（2013M540232）；中央高校基本科研业务费专项基金项目（N120817001）；教育部高等学校博士学科点博导基金项目（20120042110028）

This work was supported by the Major Program of the National Natural Science Foundation of China（61433008），the National Natural Science Foundation for Young Scholars（61202088），the Science Foundation of China for Post－doctor（2013M540232），the Fundamental Research Funds for the Central Universities（N120817001），and the PhD Programs Foundation of Ministry of Education of China（20120042110028）．