MNR算法参数分析

周旭胜（铜陵学院，安徽 铜陵 244061）



MNR算法参数分析

周旭胜
（铜陵学院，安徽 铜陵 244061）

摘 要：电阻抗断层成像技术（Electrical Impedance Tomography， EIT）是一种有着广泛应用前景的医学成像技术。论文在介绍了EIT测量原理的基础上，给出了修正的Newton-Raphson迭代算法步骤，讨论了影响MNR算法结果的两个参量。最后通过仿真实验表明，迭代步长和正则化参数均对MNR算法结果有着一定的影响，在进行逆问题研究时应综合考虑，获得最优结果。

关键词：断层；算法；参量；仿真

1　概述

1.1EIT概念

EIT是Electrical Impedance Tomography的简称，是一种反映生物体内不同器官或组织阻抗变化分布情况的新兴医学成像技术［1］。EIT技术特点很多：硬件设备体积小、质量轻、方便携带；注入电流很小，是一种无损伤成像技术；功能成像，即EIT反映的是生物体组织和器官功能性变化的特点［2］。

1.2理论依据

生物体内不同的组织具有不同的电导率，EIT技术反映的是电导率的变化情况，在频率为20～100KHz情况下人体内不同组织的电导率分布也不同。

1.3原理框图

EIT的实现过程为：给生物体表的电极注入微小电流，测量体表电压并做预处理；依据某种技术计算出电导率的分布情况；送至终端显示打印出来。数据处理和图像重构是整个EIT技术研究的两个核心单元。通常这两个过程又称为正问题求解和逆问题研究。

2　修正的Newton-Raphson迭代算法

2.1逆问题求解

正问题的求解可以通过有限元计算方法来进行，实现过程简单。但逆问题的求解则不同，因为其具有不适定性［4］，边界电压的微小扰动就会造成解的极大波动，所以只能通过迭代算法来寻找最接近真实解的近似值。

迭代算法有很多，如最速下降法、Newton-Raphson算法和修正的 Newton-Raphson （Modified Newton-Raphson， MNR）迭代算法［5］等，MNR算法对图像重构效果最好。

假设一组训练样本集z1,z2,…,zL，zi=(i,bi)表示目标回波i，bi={0,1}为该目标回波是否异常的标记，1表示异常，0表示正常，L为训练样本集个数。

2.2MNR算法

MNR算法过程是先定义目标函数，根据一定的规则找出函数的近似解。

假设目标函数为

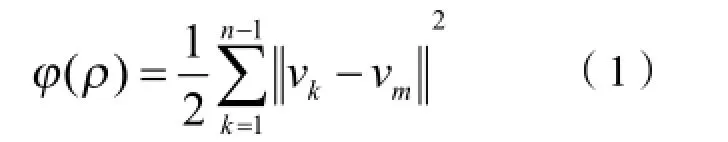
vm为第m此测量所得到的电压值，vk为相应的正问题所得到的电压测量值，则修正Newton-Raphson迭代算法步骤为：

（1）定义电导率初始值ρk；

（2）正问题求解得到vk；

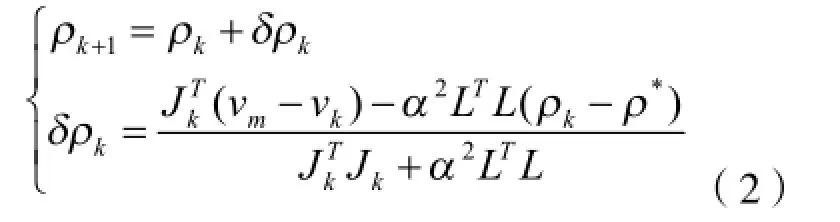
计算出新的电导率ρ1+k，重复步骤2）和3），直至满足给定条件为止。

式（2）中，L为正则化矩阵，α为正则化ρ*ρ系数，J是的预估值，是雅可比矩阵。

3　仿真结果分析

本次实验使用matlab软件平台，仿真对象为16×16的测量电压数据矩阵，系统电极数为16，电流注入方式为临近注入。

（1）迭代步长不变，不同正则系数α对成像结果影响。

设置步长k=6，仿真得α=0.2，0.02，0.002， 0.0002时的重构结果。

图1　正则化参数α分别为0.2，0.02，0.002，0.0002重建图像

（2）正则系数不变，不同的迭代步长k对成像结果影响。

步长α=0.02，迭代步长k= 2，5，8，11时的重构结果。

图2　迭代步长k=2，5，8，11

（3）结论

①从图3可以看出，当迭代步长k一定时，重构图像分辨率随着正则系数α的减小而增大，效果较为明显。

②从图4可以看出，当正则系数α一定时重构图像分辨率随着迭代步长k的增大而增大，效果没有α变化带来的效果那么明显。

③迭代步长k不能无限增大。k值越大，所带来的计算量就会增大，实际表现为计算机运算速度减慢。

4　发展趋势

EIT技术的研究还停留在单频、二维的基础上，国内外对多频［6］、三维EIT的研究成果还不多。MNR算法静态成像算法，并不适用于动态成像，这就为以后的研究工作提供了一些方向。

（1）三维EIT。当生物体内有一定电流流过时，其传输路径并不在一个平面上传输，而是分布在一个三维空间内。因此，只有三维EIT才能正确的反映生物组织阻抗的分布情况。

（2）多频EIT。不同的频率对其电导率的分布情况影响很大。多频情况下获得的体内特性参数要比单频情况丰富很多。因此，多频EIT具有很大的研究空间。

（3）动态成像。传统的静态成像算法对测量系统的要求较高。而动态成像原理是利用两组测量边界数据的差值来进行成像的。它的特点是通过差分除去系统误差，提高了系统对具体目标形状的鲁莽性。

参考文献：

［1］D.C.Barber，B.H.Brown. Applied potential tomography. Phy.E and Sci.Instru， 1984 （17）∶723-733

［2］David S Holder. ELECTRICAL IMPEDANCE TOMOGRAPHY. Series in Medical Physics and Biomedical Engineering. 1st ed.London∶Institute of Physics Publishing，2005

［3］黄嵩，何为. 电阻抗成像中变差正则化算法的研究. 生物医学工程杂志. 2006，23（6）∶1153-1156

［4］吴太旗，邓凯亮. 一种改进的不适定问题奇异值分解法. 武汉大学学报. 2011，36（8）：900-903

［5］尤富生，董秀珍，史学涛. 电阻抗断层成像中临近和对向驱动模式的研究. 第四军医大学学报，2004，25（1）∶88-91

［6］侯文生，彭承琳. 阻抗断层成像中的图像重建技术. 生物医学工程学杂志. 2000，17（2）∶214-217

（责任编辑：廖建勇）

中图分类号：C39

文献标识码：A

doi:10.3969/j.issn.1672-7304.2016.01.060

文章编号：1672–7304（2016）01–0127–02

作者简介：周旭胜（1986-），男，安徽安庆人，研究方向：点阻抗断层成像。

The Parameter Analysis of The MNR Algorithm

ZHOU Xu-sheng
（Tongling University， Tongling Anhui 244061）

Abstract:Electrical Impedance Tomography is a new Medical imaging technology with wide application prospect. The thesis introduces the theory of Electrical Impedance Tomography， gives the steps of the Mo- dified Newton-Raphson iteration algorithm，and discusses the influence that different parameters brings based on Matlab. The simulation result shows that a clearer image could be obtained based on the modified Newton-Raphson iteration algorithm， in order to get the best result， both of the parameters should be considered.

Key words:Tomography； algorithm； parameter； simulation