带腹板开洞组合梁的非线性分析

杨洪志， 周东华

(辽宁省城市建筑设计院，辽宁沈阳 110016)



带腹板开洞组合梁的非线性分析

杨洪志， 周东华

(辽宁省城市建筑设计院，辽宁沈阳 110016)

【摘要】腹板开洞钢-混凝土组合梁在国外工程中已广泛应用，它能够充分利用净空从而降低成本，但腹板开洞使得组合梁计算变得复杂。为研究腹板开洞组合梁的受力性能，采用有限元软件ANSYS建立模型，计算和分析洞口大小、位置、形状对组合梁塑性极限承载力的影响，总结其变化规律。

【关键词】带腹板开洞组合梁；轴向应变；极限承载力；挠度

在组合梁腹板上开洞，让水平管道设施穿越其洞口，可以减少管道对建筑空间的占用，增加净空，节省工程造价，因此在国内外的高层及大跨度建筑结构中广泛应用。组合梁腹板开洞后，在洞口区域总是存在拉、压、弯、剪的共同作用，加之考虑材料的非线性，使得计算变得复杂，除此之外还有很多其他因素可影响洞口处的受力情况，如洞口大小、位置和形状等。本文采用有限元软件ANSYS，模拟分析了洞口大小、位置和形状对带腹板开洞组合梁塑性极限承载力的影响。

1组合梁有限元模型

1.1单元类型及材料的本构关系

混凝土采用SOLID65单元来模拟，钢筋采用LINK8三维杆单元建模，选取线性单元SOLID45来模拟钢梁翼缘，钢梁腹板采用线性单元PLANE42模拟，钢-混凝土组合梁界面上的剪切连接件(如栓钉)可用弹簧单元COMBIN39来模拟。混凝土采用《混凝土结构设计规范》建议的应力-应变关系模型，钢材的本构关系采用二折线形成的弹性-强化模型。

1.2截面尺寸及有限元模型

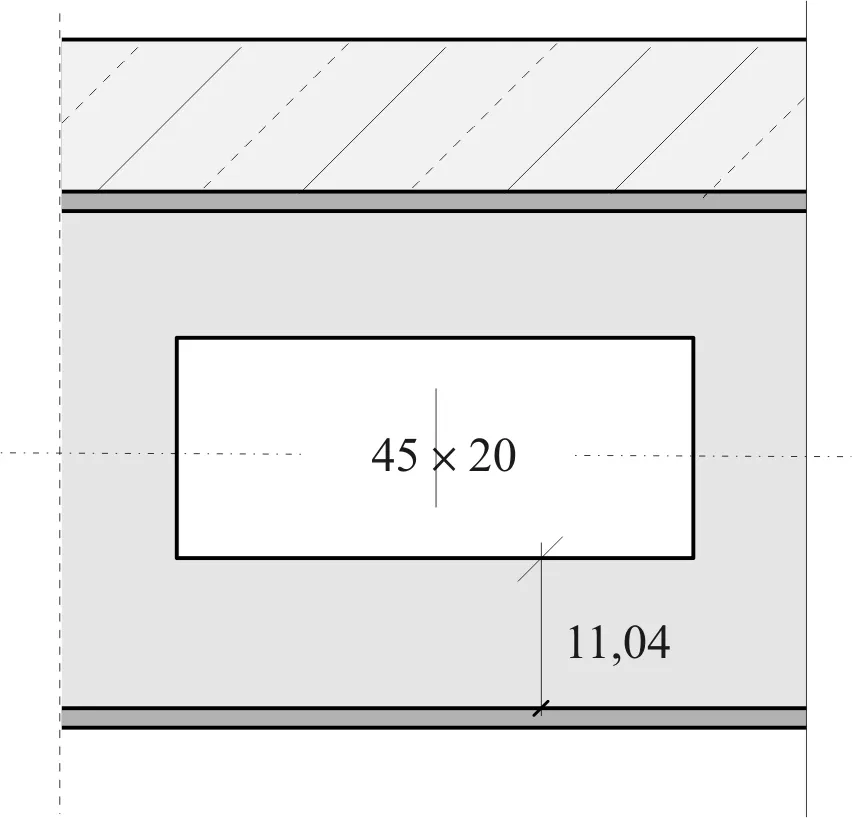
算例：一简支组合梁，梁长L=420 cm，混凝土翼板上受集中荷载P作用。混凝土:fc=29.8 MPa，ft=2.98 MPa，Ec=3×104MPa；钢筋:fy=500 MPa；钢梁:fy=240 MPa，Es=2.1×105MPa；钢梁断面：45 cm×19 cm×0.94 cm×1.46 cm。组合梁计算简图及截面尺寸见图1。

2影响带腹板开洞组合梁非线性的主要参数

2.1洞口大小

洞口大小对带腹板开洞组合梁承载力产生影响，图2为不同洞口大小变化的三种组合梁形式。

2.1.1洞口大小对组合梁挠度、极限承载力的影响

图1　组合梁计算简图及截面尺寸(单位: cm)

极限荷载和刚度是衡量梁性能的两个重要指标，图3给出了以上三种洞口大小的荷载-挠度曲线，为了更加直观的认识到洞口的削弱作用，将无洞口时的情形也绘于图中。从图3中可以看出，2a=90 cm的梁的极限承载力远远小于洞口宽度为2a=30 cm的梁的极限承载力；荷载-挠度曲线的变化规律为洞口越大，刚度越小。于是可有以下结论：随着洞口的增大，组合梁的极限承载力和刚度都有不同程度的下降，但极限承载力的下降尤为明显。

将削弱后结构的极限承载力与未削弱(无洞口时)的极限承载力对比，由此可以从定量的角度看出洞口大小对极限承载力的削弱程度(表1)。

表1　有洞口与无洞口时的承载力比较

2.1.2梁洞口上边缘(I—I剖面)的轴向应变(εx)沿梁长的分布

(a) 组合梁1

(b) 组合梁2

(c) 组合梁3图2　洞口大小变化的组合梁(单位：cm))

图3　不同洞口大小的荷载-挠度曲线

图4　组合梁1沿I—I截面上的轴向应变

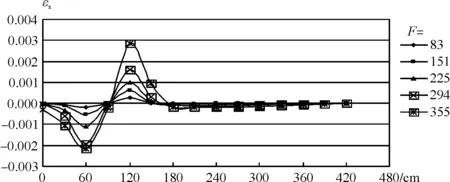
图5　组合梁2沿I—I截面上的轴向应变

图6　组合梁3沿I—I截面上的轴向应变

从应变正负号的变化可看出，在洞口左右边缘处的应变主要是由次弯矩引起的，因为它们的作用方向与次弯矩的一致，即洞口左边缘处的次弯矩是负弯矩，该弯矩引起部分截面上部受拉、下部受压；洞口右边缘处的次弯矩是正弯矩，该弯矩引起部分截面上部受压、下部受拉；通过对比图4～图6可以看出，随着洞口大小的不断增大，不同高度水平截面的轴向应变不断增大，这说明不仅应变的正负号而且应变的大小也是由次弯矩决定的。这从另一个方面也说明，在洞口左右边缘处主弯矩的作用较小。

2.2洞口位置

以洞口中心与支座的距离lm来反映洞口的位置。为了弄清洞口位置对梁承载力的影响，对三种不同洞口位置的梁进行了计算，梁的计算简图及截面尺寸如图7所示。

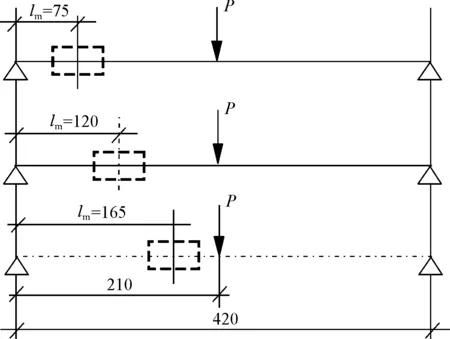
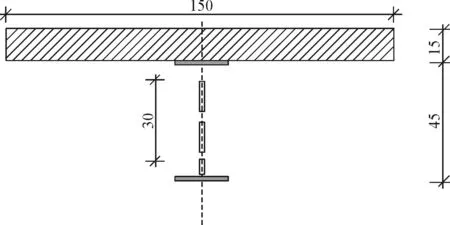
图7　梁的计算简图及截面尺寸(单位:cm)

三种不同洞口位置的荷载、挠度值计算结果见表2。

表2　不同洞口位置的荷载、挠度值

2.2.1洞口位置对组合梁挠度、极限承载力的影响

同样地，将图7所示的三种情况的荷载-挠度曲线与无洞口时的荷载-挠度曲线均绘于图8。从图8中可以看出：洞口越靠近支座，其承载力越高，并且挠度值越大。lm=165时组合梁的极限承载力远小于无洞口时的极限承载力，挠度值也最小，说明洞口越靠近集中荷载作用处，组合梁越容易破坏，极限承载力降低最大，并且变形能力下降最快。

图8　不同洞口位置的荷载-挠度曲线

2.2.2梁底边缘(I—I剖面)的轴向应变(εx)沿梁长的分布

在图9～图11中，分别给出了三个不同洞口位置时梁底边缘(I—I剖面)的轴向应变的分布。从图中应变的正负号的变化可看出，当lm=75时，洞口左边缘处的次弯矩(负)作用更为明显，并且随着洞口中心距左侧支座距离的增大，洞口右边缘处的次弯矩(正)作用更加明显。

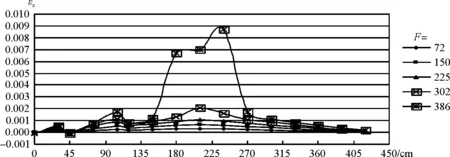
图9　lm=75时沿I—I截面上的轴向应变

2.3洞口形状

通过前面的计算可以清楚地认识到洞口大小及洞口位

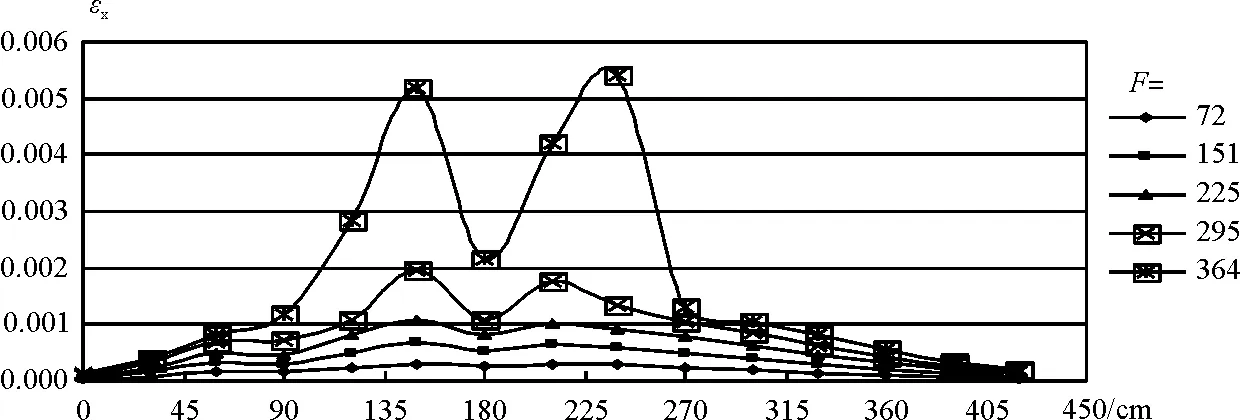
图10　lm=120时沿I—I截面上的轴向应变

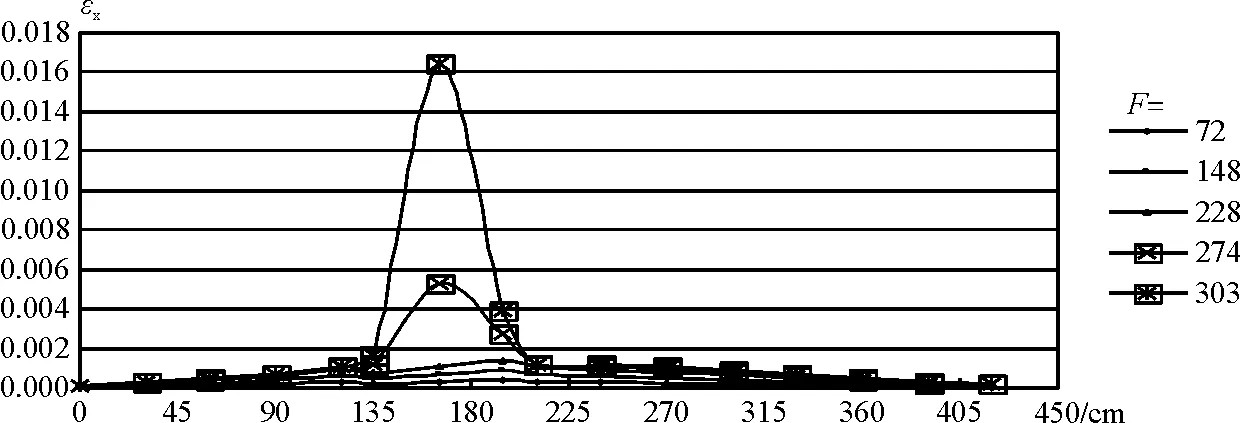
图11　lm=165时沿I—I截面上的轴向应变

置对组合梁承载力的影响，但是，以同样面积在钢梁腹板上开不同形状的洞口对承载力有什么样的影响呢？带着这样的问题，本文对五种不同洞口形状的梁进行了计算，计算时所选梁的计算简图及截面尺寸如图12所示，洞口形状如图13所示，不同洞口形状的组合梁有限元模型如图14所示。

图12　梁的计算简图及截面尺寸(单位: cm)

第一种

第二种

第三种

第四种

第五种图14　五种不同洞口形状的组合梁有限元模型(1/2)

2.3.1洞口形状对组合梁挠度、极限承载力的影响

图13中五种洞口形状的计算结果见表3。

表3　不同洞口形状的荷载、挠度值

同样地，将图14所示的五种洞口形状的荷载-挠度曲线与无洞口时的荷载-挠度曲线均绘于图15。从图15中可以看出，同等面积的不同形状洞口对组合梁的极限承载力有不同程度的削弱，其中，第二种形状的洞口(菱形)对组合梁的极限承载力削弱程度最大，其次是第五种形状的洞口(矩形)。并且从表3的计算结果和图15能看出，第一种形状的洞口(圆形)对组合梁的极限承载力削弱程度最小。所以可以直观的得到这样的结论：开同等面积的不同形状的洞口，以圆形洞口对组合梁极限承载力削弱程度最小，菱形洞口对组合梁极限承载力削弱程度最大；由有限元模型可以看出，第二种和第五种形状洞口的边节点离钢梁翼缘边缘最近，因此，两种洞口形状组合梁最容易破坏，也是因此对极限承载力削弱程度最大。

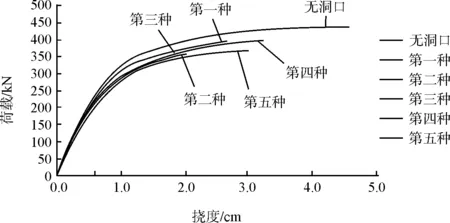
图15　不同洞口形状的荷载-挠度曲线

2.3.2梁底边缘(I—I剖面)的轴向应变(εx)沿梁长的分布

在图16中，分别给出了五种不同洞口形状的组合梁沿

(a)第一种洞口形状组合梁沿I—I截面上的轴向应变

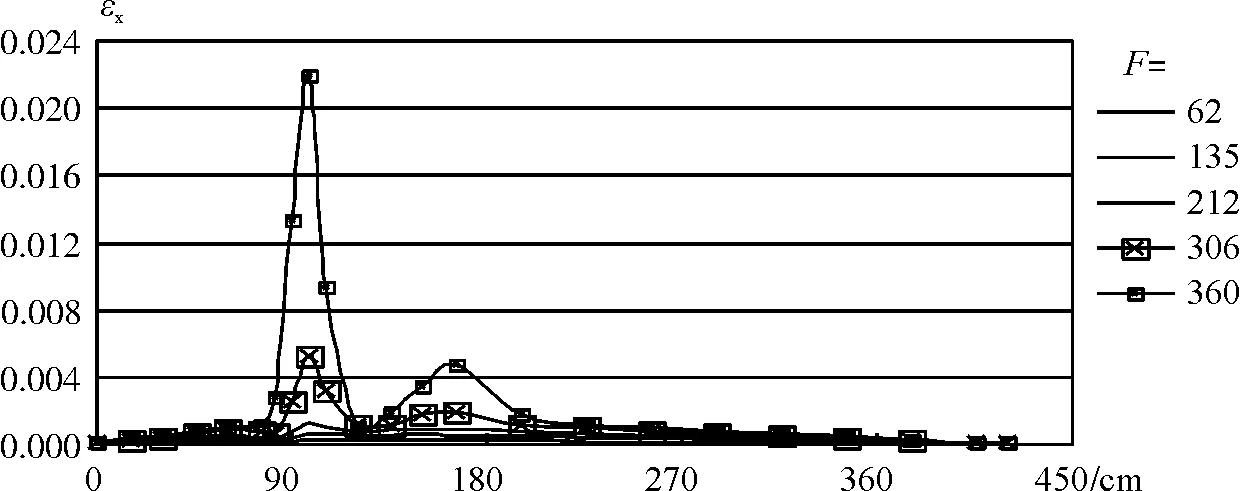
(b)第二种洞口形状组合梁沿I—I截面上的轴向应变

(c)第三种洞口形状组合梁沿I—I截面上的轴向应变

(d)第四种洞口形状组合梁沿I—I截面上的轴向应变

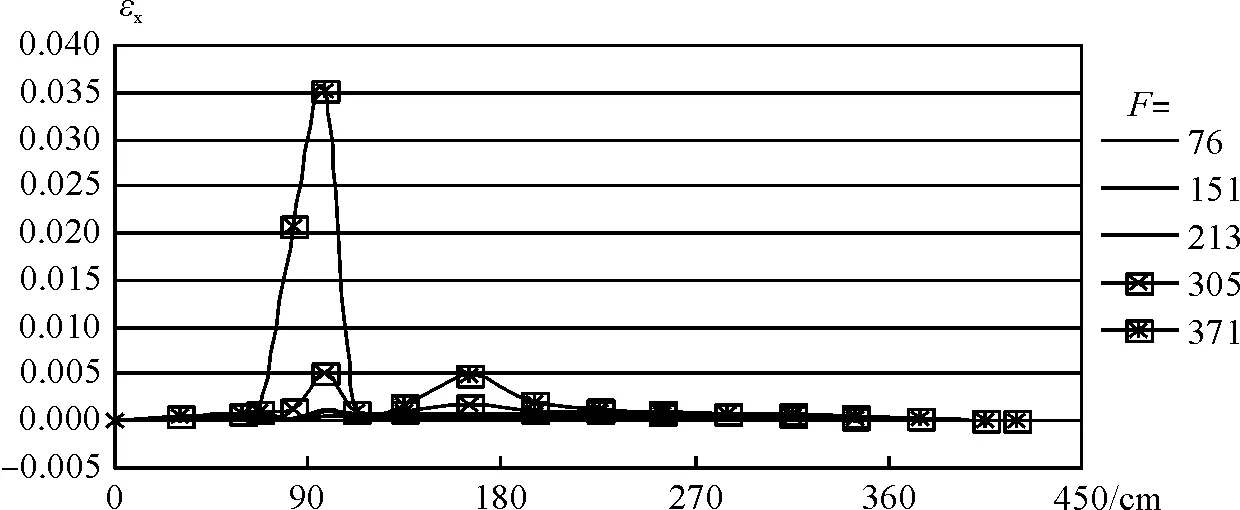
(e)第五种洞口形状组合梁沿I—I截面上的轴向应变(εx)图16　不同洞口形状组合梁沿梁长的轴向应变(εx)的分布

梁的底边缘(I—I剖面)的轴向应变分布。从图中应变的正负号的变化可看出，次弯矩作用规律同不同洞口大小和不同洞口位置有关。从图中应变的大小可以看出，第二种和第五种洞口形状的组合梁的轴向应变最大，可以得到这样的结论：开第二种和第五种形状的洞口对组合梁最不利。

3结论

(1)随着洞口的增大，组合梁的极限承载力和刚度都有不同程度的下降，但极限承载力的下降尤为明显。

(2)随着洞口大小的不断增大，不同高度水平截面的轴向应变不断增大，这说明不仅应变的正负号而且应变的大小也是由次弯矩决定的。

(3)洞口越靠近集中荷载作用处，组合梁越容易破坏，极限承载力降低最大，并且变形能力下降最快。

(4)开同等面积的不同形状的洞口，以圆形洞口对组合梁极限承载力削弱程度最小，菱形洞口对组合梁极限承载力削弱程度最大。

参考文献

[1]刘坚，周东华，王文达.钢与混凝土组合结构设计原理[M].北京：科学出版社，2005.

[2]聂建国，刘明，叶列平.钢-混凝土组合结构[M].北京：中国建筑工业出版社，2005.

[3]周东华，赵惠敏.带腹板开洞组合梁的非线性计算[J].四川建筑科学研究，2004，30(2).

[4]杨洪志，周东华.剪切连接度对组合梁工作性能的影响[J]. 山西建筑,2014,40(32).

[5]王鹏，周东华.腹板开洞钢-混凝土组合梁非线性有限元分析[J].沈阳建筑大学学报:自然科学版，2011,27(5).

[作者简介]杨洪志(1981～)，男，硕士，工程师，从事建筑结构设计工作；周东华(1957～)，男，博士后，主要从事特殊形式的组合结构研究。

【中图分类号】TU399

【文献标志码】A

[定稿日期]2015-10-13