柱桩与摩擦桩刚度差异分析研究

邱朝阳

(中铁二院工程集团有限责任公司， 四川成都 610031 )



柱桩与摩擦桩刚度差异分析研究

邱朝阳

(中铁二院工程集团有限责任公司， 四川成都 610031 )

【摘要】在铁路桩基计算中，在桩底岩层极限抗压强度不高，既可以按摩擦桩计算也可以按柱桩计算的条件下，在相同桩径、桩长、桩数及布置条件下，按柱桩和摩擦桩分别计算，墩顶会得出差异较大的线刚度。文章根据桩基计算过程，分析了刚度存在差异的原因及相关原因对刚度差异的影响程度。

【关键词】柱桩；摩擦桩；线刚度；差异分析

随着我国铁路的高速发展，无缝线路被普遍采用，为了满足无缝线路的要求，无缝线路对墩顶线刚度提出了严格的限值。在墩较高、桩基表层地质条件差的条件下，线刚度往往成为控制桩基设计的主要因素，对桩径、桩数、桩基布置及承台尺寸有较大影响，直接影响工程费用。在相同条件下，按摩擦桩计算的墩顶线刚度往往比按柱桩计算的大。按摩擦桩设计已满足要求的情况下，若按柱桩设计易出现不满足要求的情况，但实际情况只会有一个，不会因为计算方法的不同而不同。为进一步研究计算上的刚度差异，对计算过程进行分析，并找出引起差异的主要原因及影响程度是必要的。

1计算过程分析

1.1计算换算深度

1.2计算A1～D4级数

桩轴线挠曲线方程、桩身各截面转角、弯矩和剪力计算需用到A1～D4十六个级数，十六个级数是由换算深度αL所决定的收敛级数，可通过编程求得。

1.3计算单桩桩顶柔度系数

δ1、δ3为桩顶作用单位横向力时，桩顶面的横向位移和转角；

δ3、δ2为桩顶作用单位力矩时，桩顶面的横向位移和转角。

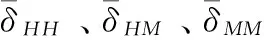
当桩底位移和转角为零时(桩尖嵌入岩层的柱桩)：

当桩底位移为零，转角可不为零时(桩底置于非岩石地基中的摩擦桩或桩底支立于岩层的柱桩)：

1.4计算桩基础中单桩桩顶刚度系数

ρ1为当承台底面沿桩轴线方向作单位位移时，所引起的桩顶轴向力；

ρ2为当承台底面沿桩轴线方向的垂直方向作单位位移时，所引起的桩顶横向力；

ρ3为当承台底面沿桩轴线方向的垂直方向产生单位位移时，所引起桩顶处的弯矩；或当承台底面在桩顶处转单位转角时，所引起桩顶处的横向力；

ρ4为当承台底面在桩顶处转单位转角时，所引起桩顶处的弯矩。

式中：A0表示桩底土的受压面积;ε表示折减系数。

柱桩：ε=1时， A0取桩底面积A0=0.25πd2。

钻孔摩擦桩：ε=0.5时， A0取桩身由地面按1/4内摩擦角扩散至桩底的底面积。当底面积大于桩尖中心距离之间的面积时，取桩中心之间的面积。A0=0.25πD2，D=min(d+2Ltan(φ/4),Ljj)，Ljj表示最小桩间距。

1.5计算群桩桩顶的刚度指标

群桩顶刚度指标有γbb、γab、γβb、γba、γaa、γβa、γbβ、γaβ、γββ共9个。

γbb、γab、γβb表示承台产生单位竖向位移时，所有桩桩顶作用于承台底的竖向、水平力、弯矩之和。

γba、γaa、γβa表示承台产生单位水平位移时，所有桩桩顶作用于承台底的竖向、水平力、弯矩之和。

γbβ、γaβ、γββ表示承台绕过底面的形心轴转单位角时，所有桩桩顶作用于承台底的竖向、水平力、弯矩之和。

铁路桩基多为具有两个对称轴的竖直桩，这种情况下:

γba=γab=0γbβ=γβb=0

γbb=∑ρ1γaa=∑ρ2+b0Ac

γββ=∑ρ4+∑x2ρ1+b0Ic

γaβ=γβa=-∑ρ3+b0Sc

1.6计算承台变位及墩顶综合线刚度

2影响因素分析

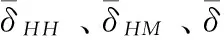
(1)假定桩基的地质情况：

第一层为黏土，厚度为桩长减4 m，地基系数的比例系数m=10 000 kPa/m2，内摩擦角φ=10°。

第二层为泥岩，厚度大于4 m，地基系数的比例系数m=50 000 kPa/m2，内摩擦角φ=42°。

基本承载力σo=500 kPa，极限抗压强度R=4.5 MPa，竖向地基系数Co=244 3750 kPa/m。

(2)假定桩基的布置情况：

承台顺桥向长5.7 m，横桥向长9.0 m，承台高2.0 m，6根1.25 m桩行列式布置，桩间距3.4 m。

(3)假定墩高及墩顶线刚度：

墩底到顶帽顶15 m，垫石高0.42 m，垫石顶处墩身线刚度339.2 kN/cm。

柱桩与摩擦桩墩顶综合线刚度对比见图1。

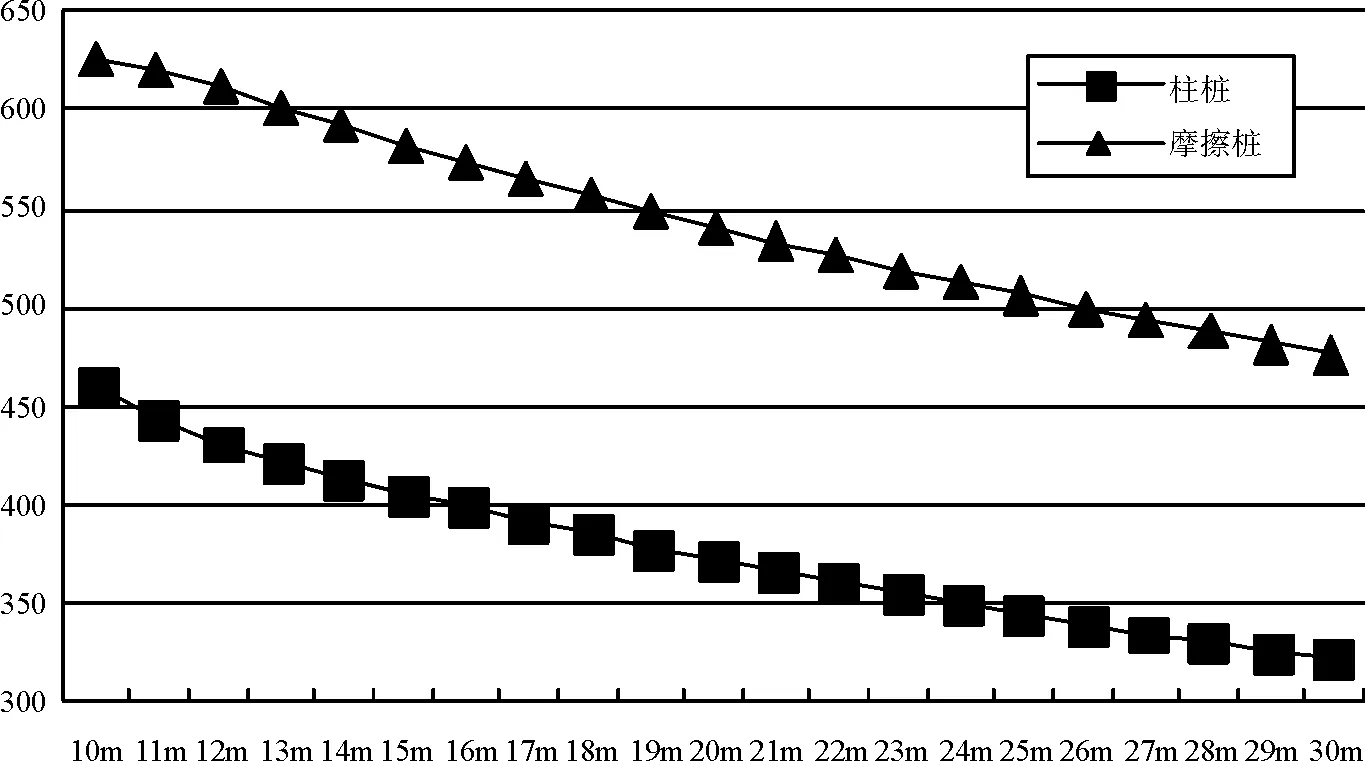
图1　柱桩与摩擦桩墩顶综合线刚度对比

由图1可见，相同条件下分别按柱桩和摩擦计算，得出的墩顶线刚度差异较大，下面分四种情况测试两个影响因素的影响程度。

2.1测试桩底边界条件对刚度的影响程度

(1)柱桩。

桩底由不可转动改为可转动，刚度曲线见图2。

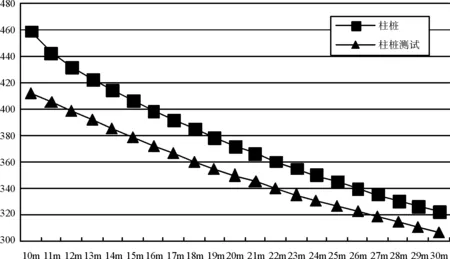
图2　柱桩桩底可转动的刚度曲线

桩底由不可转动改为可转动后刚度变小是因为换算长度变长了，柱桩是假定基岩面处的转角和位移为零，换算长度是α×(L-嵌岩深度)，现改到桩底后换算长度是α×L，引起了桩顶水平刚度的减少。

(2)摩擦桩。

桩底由可转动改为不可转动,刚度曲线见图3。

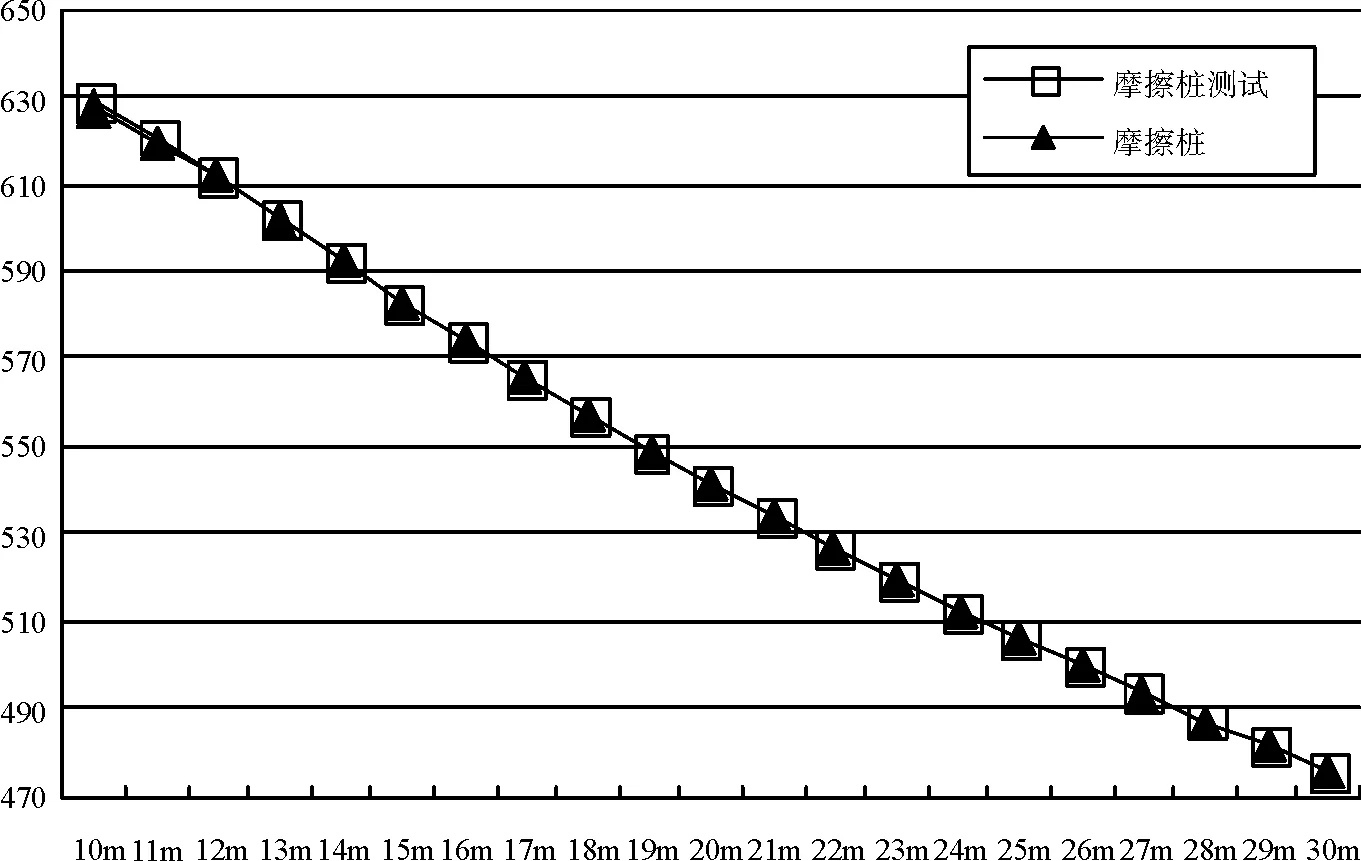
图3　摩擦桩桩底不可转动的刚度曲线

桩底由可转动改为不可转动，桩长超过一定深度后对刚度无影响，与换算深度α×L>4时，桩身变位及内力与桩底支承条件的关系不大的定论一致。

2.2测试桩身及桩底土弹性压缩对刚度的影响程度

(1)柱桩。

桩身计算受压长度系数ξ取0.5，桩底受压面积取按φ/4扩散角且最大不大于桩间距计算，刚度曲线见图4。

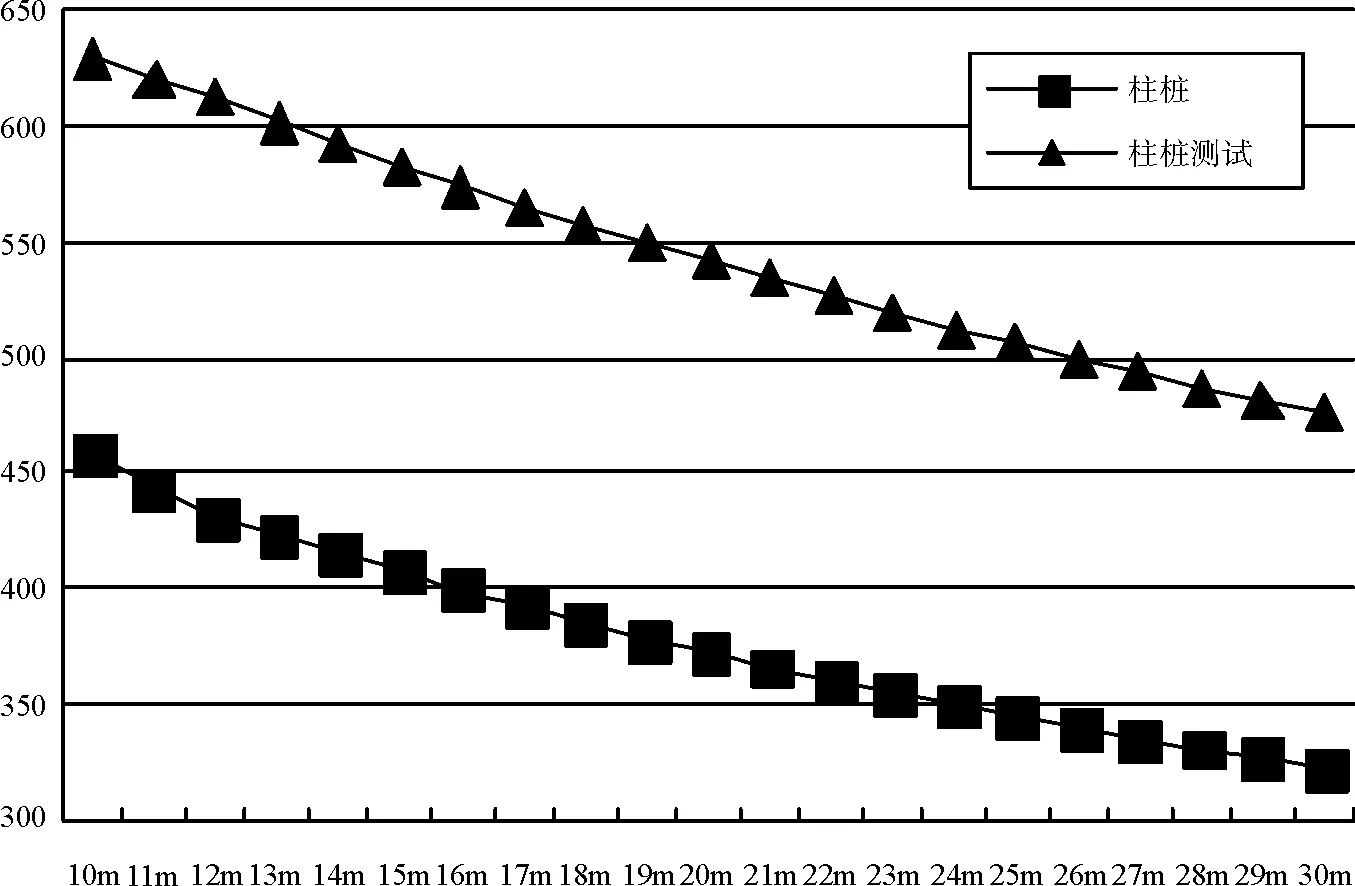
图4　柱桩桩身及桩底土弹性压缩的刚度曲线

桩身及桩底土弹性压缩采用摩擦桩的假定条件计算后，刚度大幅提高，与摩擦桩的刚度基本一致。

(2)摩擦桩。

桩身计算受压长度系数ξ取1，桩底受压面积取按桩底直径计算，刚度曲线见图5。

图5　摩擦桩桩身及桩底土弹性压缩的刚度曲线

桩身及桩底土弹性压缩采用柱桩的假定条件计算后，刚度大幅减少，与柱桩的刚度基本一致。

3结论

(1)相同条件下摩擦桩与柱桩刚度差异大的主要原因是桩身及桩底土弹性压缩的假定不同。

(2)相同条件下摩擦桩与柱桩刚度差异大的次要原因是桩底边界条件的假定不同，此原因的影响甚微，桩长大于一定深度后无影响。

(3)相同条件下柱桩与摩擦桩刚度差异有30%～50%，存在一定的不合理性，实际刚度只会是一个，不会因计算方法的不同而不同，究竟是柱桩的假定接近实际还是摩擦桩的假定接近实际，需进一步建立课题实测研究。

(4) 相同条件下摩擦桩刚度比柱桩大的主要原因是柱桩桩身及桩底土弹性压缩比摩擦桩的大，柱桩桩身压缩大是因为桩身不考虑摩擦力影响，计算受压长度系数ξ取1，而摩擦桩桩身计算受压长度系数考虑了摩擦力影响，计算受压长度系数ξ取0.5。柱桩顶在竖向力作用下桩身的弹性压缩与土层之间同样会产生相对位移，不考虑基岩面以上桩身摩擦力影响存在一定的不合理性。柱桩桩底土弹性压缩大是因为桩底计算面积比摩擦桩的小，柱桩桩底土压缩面积采用的是桩底面积，而摩擦桩桩底土压缩面积由于考虑了摩擦力对桩侧土的作用，采用的是扩散面积，最大面积是桩间距的圆周面积，比柱桩的大，从而引起了压缩量的减少，增加了桩的竖向刚度。从分析可知，摩擦桩压缩量比柱桩还小导致了刚度比柱柱大，目前规范的假定存在一定的不合理，需建立课题实测研究相关假定及相关假定的取值。

参考文献

[1]汤康明. 基础工程[M]. 成都：西南交通大学出版社, 1990.

[2]TB 10002.5-2005 铁路桥涵地基与基础设计规范[S].

【中图分类号】TU473.1+2

【文献标志码】A

[定稿日期]2016-03-01