基于SOLIDWORKS和V的半球型气体动压轴承三维建模

姜维，于晓凯，葛世东，屈驰飞，孙北奇

(1.洛阳轴研科技股份有限公司，河南 洛阳 471039；2.河南省高性能轴承技术重点实验室，河南 洛阳 471039；3.滚动轴承产业技术创新战略联盟，河南 洛阳 471039)

半球型气体动压轴承由于球面本身具有自对准性，其对几何失调的敏感程度小，工作姿态角趋于零，大大降低了陀螺仪的系统误差，在高精度、长寿命陀螺仪中应用广泛[1]。光滑球面不能承受轴向载荷，并且具有半速涡动，为提高半球气体动压轴承轴向刚度和抑制半速涡动，在进气口两端对称设计了等角螺旋槽。

1 半球型气体动压轴承的建模分析

半球型气体动压轴承设计时，需首先建立带等角螺旋槽轴承的三维模型，再进行半球型气体动压轴承的仿真分析。SOLIDWORKS不能直接绘制等角螺旋槽，仍需借助参数化分析生成用于建模所需的球面等角螺旋槽。

半球型气体动压轴承的球面分为槽区和台区，如图1和图2所示。α为等角螺旋槽的螺旋角；θ0为半球球台小端圆的纬度角；θ1为半球等角螺旋槽截止圆的纬度角；θ2为半球等角螺旋槽起始圆的纬度角；θg为同一条槽所在2条边线的夹角；b，b1分别为台区和槽区的宽度；h，h1分别为台区和槽区的深度；U为速度；球面均匀刻有Ng个螺旋槽，槽台比为b1/b，则每个槽的2条边线之间的夹角为πb1/[Ng(b1+b)]。

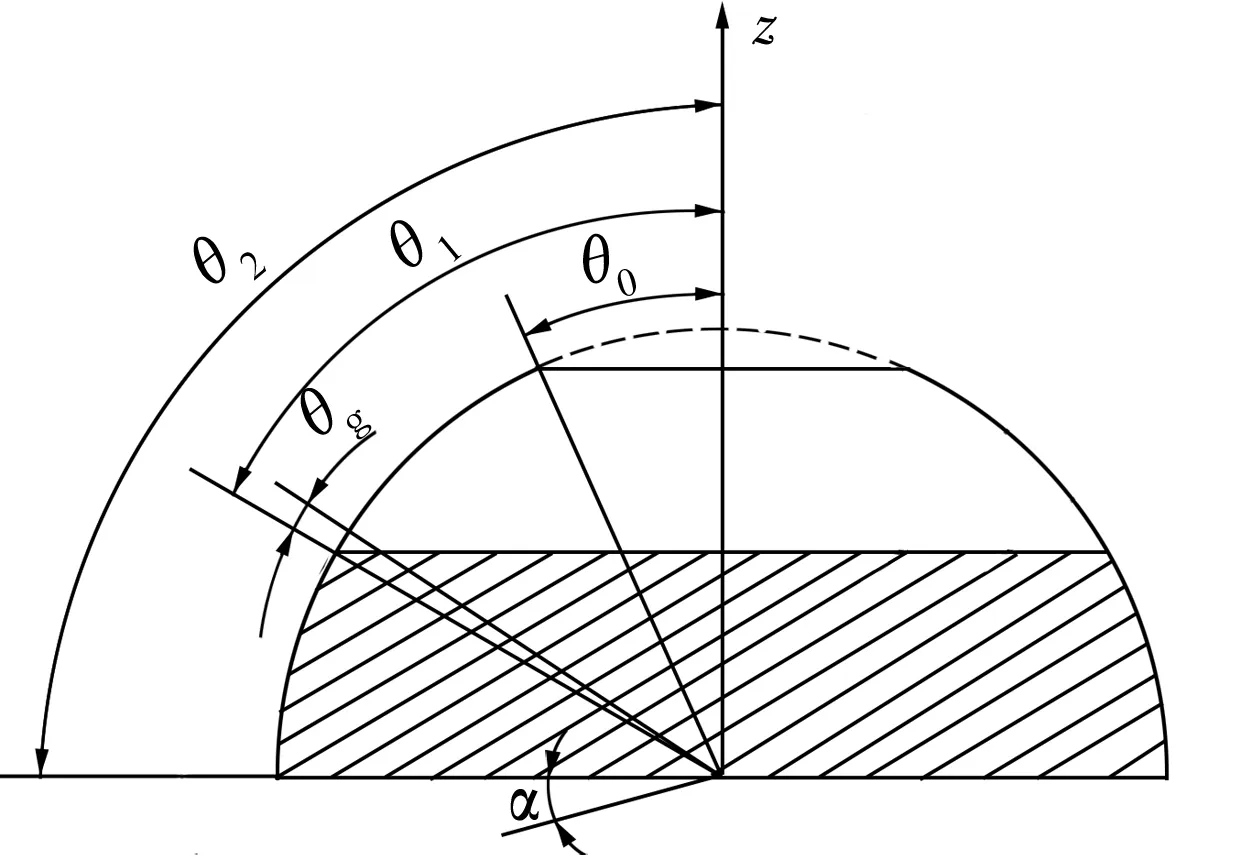
图1 半球型轴承螺旋槽的区域划分

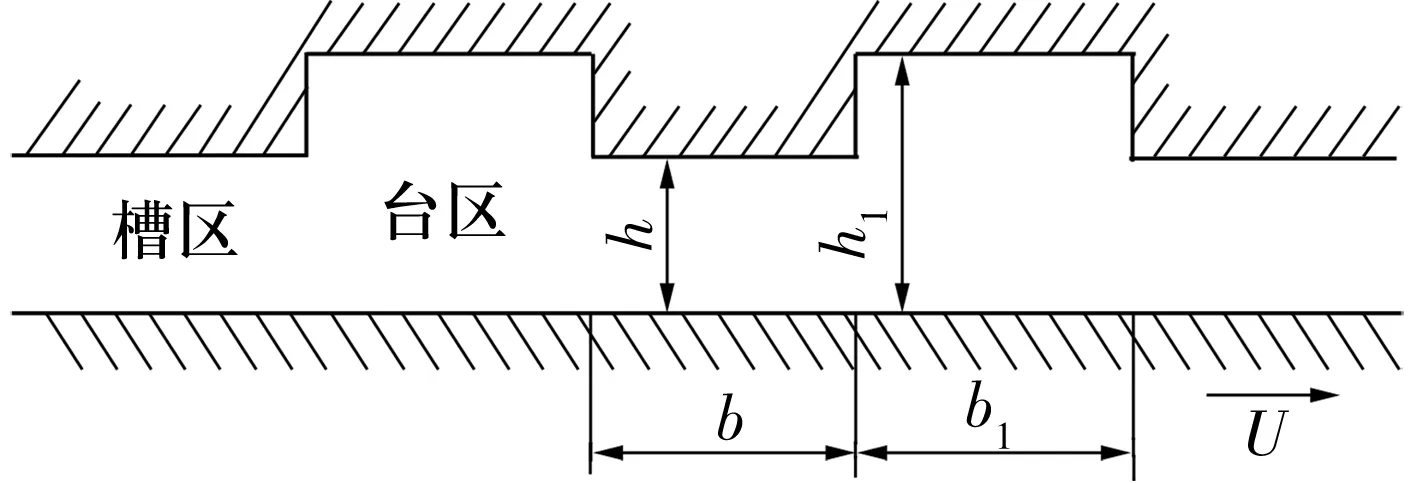
图2 螺旋槽尺寸

1.1 球面等角螺旋线的参数方程

球面等角螺旋槽的边线(等角螺旋线)是生成等角螺旋槽的关键。如图3所示，Q为等角螺旋槽的起始点，O′为等角螺旋槽的终止点，球面等角螺旋线S的经度角φ，ψ和纬度角θ之间的参数方程为[2]

(1)

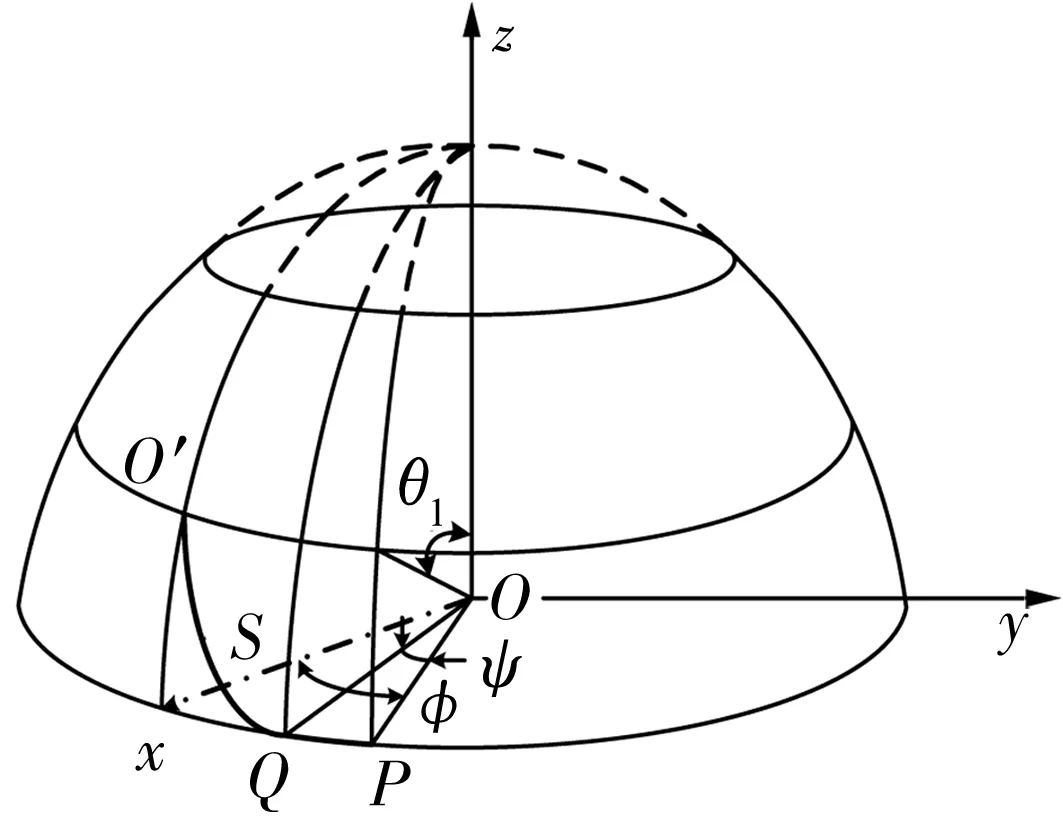
图3 半球型轴承上任意点的坐标

1.2 第1条等角螺旋槽边线的直角坐标参数方程

设球面螺旋槽第1条边线的起始点所在的经度角为0，则球面等角螺旋槽的第1条边线的参数方程为

，(2)

式中：x，y，z为等角螺旋槽第1条等角螺旋线上任意一点的坐标值；R为球面半径。

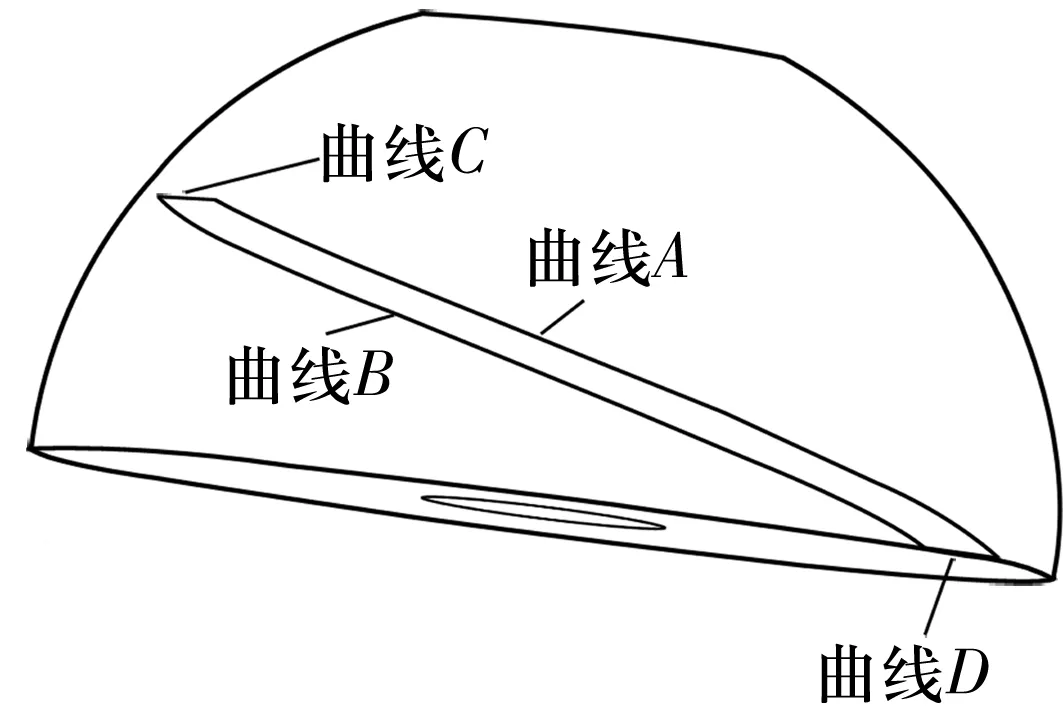
图4 球面等角螺旋槽4条边线

1.3 第2条等角螺旋槽边线的直角坐标参数方程

由于球面等角螺旋线为空间3D曲线，而SOLIDWORKS无法实现空间3D曲线的圆周阵列，故只能利用上述方法生成第2条等角螺旋线曲线B,如图4所示。其参数方程为

。(3)

1.4 第3,4条等角螺旋槽纬线的直角坐标参数方程

等角螺旋线的2条纬线也为空间3D曲线，利用上述方法生成第3,4条纬线，第3条螺旋线即曲线C的参数方程为

(4)

πb1/[Ng(b1+b)]。

第4条螺旋线(曲线D)与曲线C相同，仅φ取值范围不同， 0≤φ≤πb1/[Ng(b1+b)]。

2 建模实例

以某半球型气体动压轴承建模为例，各项参数为：半球半径为13 mm，中心孔直径为12 mm，螺旋槽角度为15°，槽宽比为1∶1，槽深为5 μm，螺旋槽起始、终止角度分别为90°，60°。

2.1 建立球模型

利用SOLIDWORKS建立半球模型如图5所示。

2.2 等角螺旋槽线的V源代码

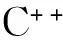
∥第1条螺旋线

∥thet[i]—槽线上不同点所在位置的纬度角；

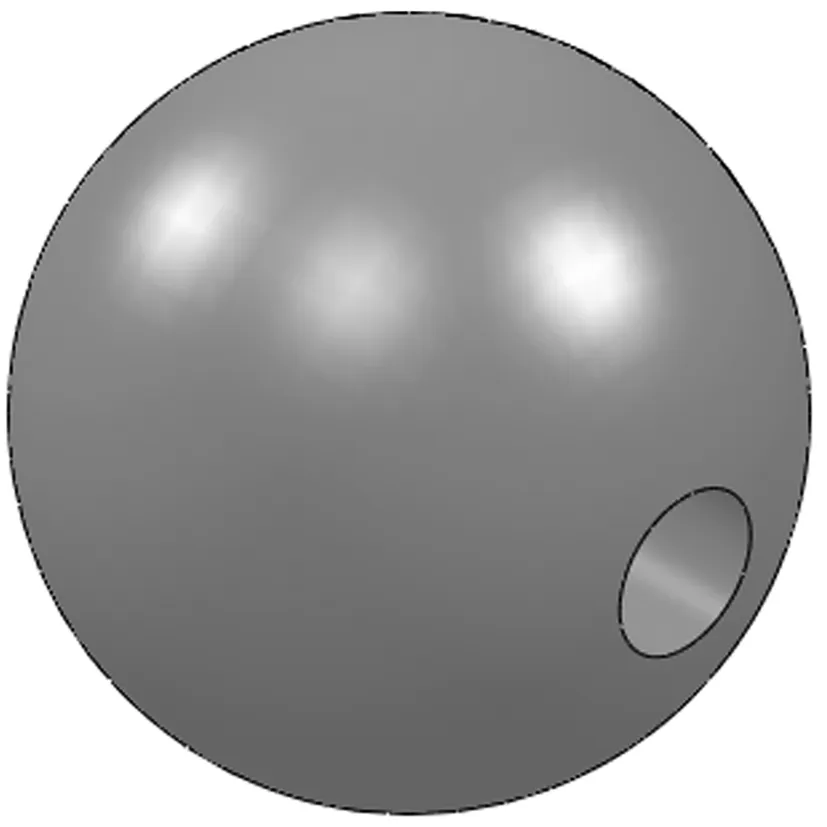
图5 半球模型

∥thet_2，thet_1—边界角；

∥alpha—螺旋角α；

∥phi[i]—球面等角螺旋槽任一点对应的经度角；

{

thet[i]=thet_2-i*(thet_2-thet_1)/100;

phi[i]=tan(alpha)*log(tan(thet[i]/2)/tan(thet_2/2));

x[i]=R*sin(thet[i])*cos(phi[i]);

y[i]=R*sin(thet[i])*sin(phi[i]);

z[i]=R*cos(thet[i]);

}

∥第2条螺旋线

{

thet[i]=thet_2-i*(thet_2-thet_1)/100;

phi[i]=tan(alpha)*log(tan(thet[i]/2)/tan(thet_2/2))+phi_0;

x[i]=R*sin(thet[i])*cos(phi[i]);

y[i]=R*sin(thet[i])*sin(phi[i]);

z[i]=R*cos(thet[i]);

}

∥第3条螺旋线

{

thet[i]=thet_1;

phi[i]=tan(alpha)*log(tan(thet[i]/2)/tan(thet_2/2))+i*phi_0/100;

x[i]=R*cos(thet_2-thet[i])*sin(thet_2-phi[i]);

y[i]=R*cos(thet_2-thet[i])*cos(thet_2-phi[i]);

z[i]=R*sin(thet_2-thet[i]);

}

∥第4条螺旋线

{

thet[i]=thet_2;

phi[i]=i*phi_0/100;

x[i]=R*cos(thet_2-thet[i])*sin(thet_2-phi[i]);

y[i]=R*cos(thet_2-thet[i])*cos(thet_2-phi[i]);

z[i]=R*sin(thet_2-thet[i]);

}

2.3 等角螺旋槽

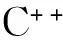
图6 导入直径13 mm的4条等角螺旋槽边线的模型

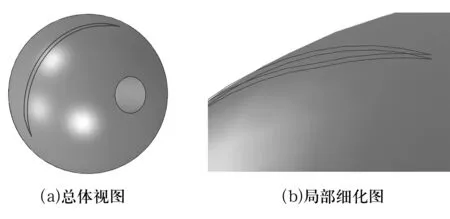
图7 导入直径12.99 mm的4条等角螺旋槽边线的模型

将直径13 mm的4条边线和直径12.99 mm的4条边线通过“组合曲线”方法构成2条组合曲线，再通过“边界切除”生成等角螺旋槽如图8所示，然后由“旋转”生成其他的螺旋槽如图9所示，最后“拉伸切除”生成半球型气体动压轴承的模型如图10所示。

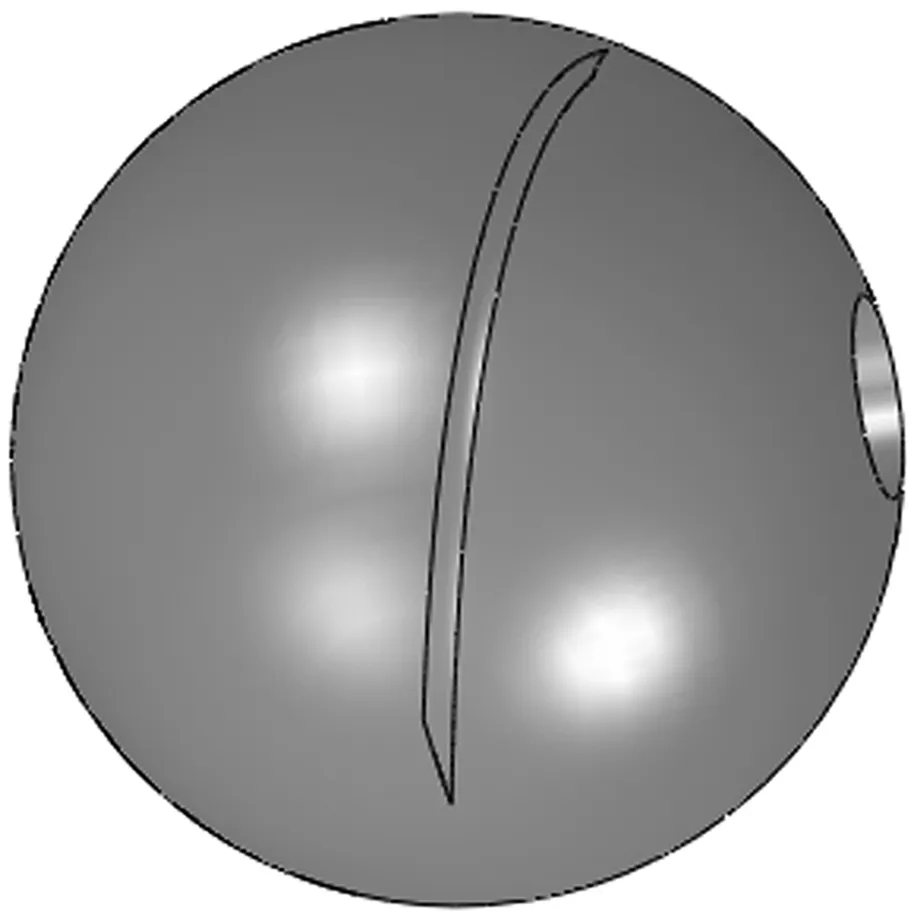
图8 1个等角螺旋槽的模型

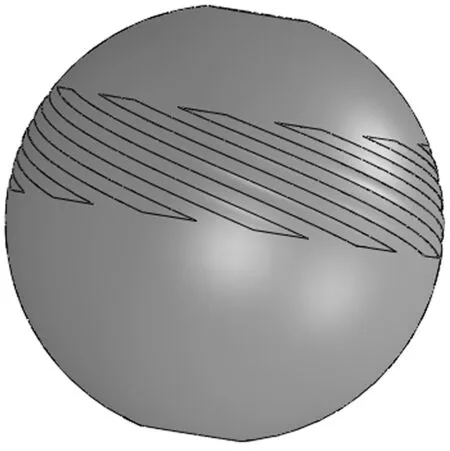
图9 全部等角螺旋槽的模型

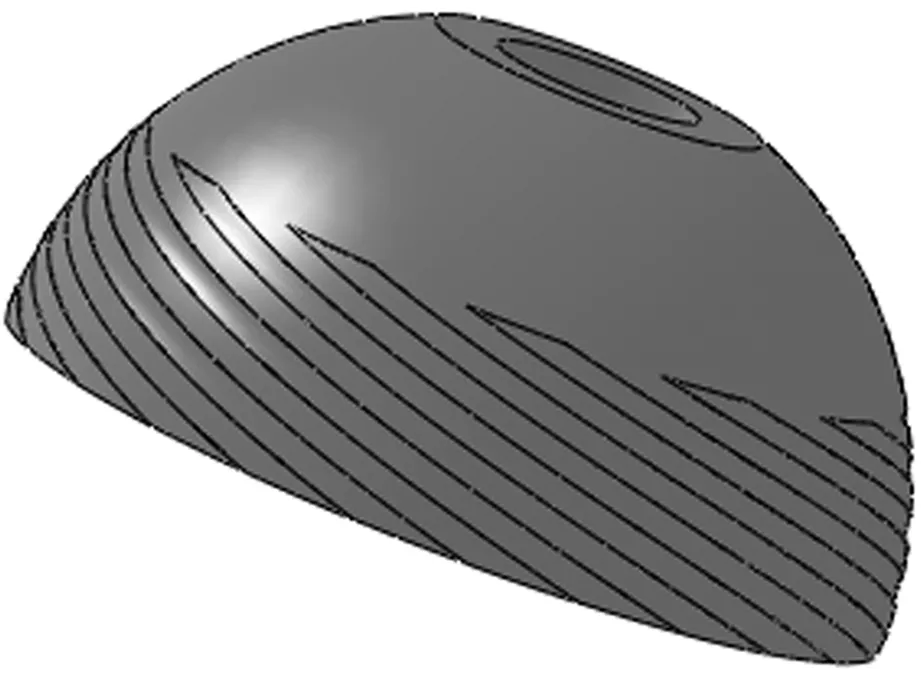
图10 半球型气体动压轴承的模型

3 结束语

半球型气体动压轴承的三维建模是进行气体动压轴承设计和分析半球型气体动压承载能力和气流稳定性的基础。通过半球型气体动压轴承的三维建模，可得到适合结构尺寸的螺旋槽结构，有助于半球型气体动压轴承的设计分析。