基于小波包和BN模型的深沟球轴承故障诊断
郭文强,张宝嵘,彭程,夏令君,佘金龙
(陕西科技大学 电气与信息工程学院,西安 710021)
随着生产技术的不断发展,造纸机作为造纸生产的关键设备,逐渐呈现大型化、自动化、连续化、复杂化的趋势,滚动轴承作为造纸机的重要零件,对造纸机的安全运行起着重要作用。国内大部分造纸机干燥部采用深沟球轴承,该轴承在工作中除转速高、承载大外,工况也极其恶劣,致使所采集信号的完整性受到影响。所获得的信息数量与质量通常受到现场测试条件等因素的限制,需要在信息不完整或不确定的情况下进行故障分析、诊断;而轴承故障特征与产生原因之间的映射关系不唯一,即一种故障原因可以产生多种故障特征或一种故障特征同时对应几种故障原因[1]。以上问题导致造纸机轴承故障诊断存在一定的不确定性。
文献[2]将谐波小波包与BP神经网络相结合,用于轴承的声发射模式识别技术;文献[3]针对轴承故障振动信号的非平稳特性,提出了一种基于局域均值分解和神经网络的故障诊断方法,但上述方法用于故障诊断的前提是整个诊断过程必须使用准确、完整的故障特征信息;文献[4]采用了基于模糊理论的诊断方法,虽然结构简单,但存在诊断模型学习能力不足的缺点。面对大规模复杂系统诊断建模和诊断决策,Bayes网络(Bayesian Network,BN)凸显出强大的适应性,并已经发展成为处理复杂系统不确定性,进行概率推理的一种有效的理论模型[5-6];而且BN采用概率值描述事件发生的可能性,能够方便地处理信息不完备问题[7-8]。
根据上述理论,提出了一种基于小波包特征向量提取和BN强大的学习和推理算法相结合的方法,用于轴承的故障诊断。
1 基本原理
1.1 小波包分析
特征提取是当前机械故障诊断中的关键问题,直接关系故障诊断的准确性和早期预报的可靠性[9-10]。小波包分解[11]能为轴承故障信号提供更加精确的分析方法,其表达式为
(1)
式中:cp(l)为原始信号,p=n/2或 (n-1)/2,n∈Z+;h(k),g(k)分别为尺度函数和小波函数对应的实系数滤波器,k∈Z。
1.2 Bayes网络
Bayes网络以概率的形式表示为B(G,P),其中G为具有m个节点(随机变量)的有向无环图,节点间的边代表随机变量间的依赖关系;P为与每个节点相关的条件概率表,表示为P(xi|p(xi)),其定量地表达了节点xi同其父节点p(xi)之间的依赖程度[12]。在BN中,定性信息主要通过网络的拓扑结构表达,而定量信息主要通过节点间的联合概率密度表示。联合概率密度P(x1,x2,…,xm)可以表示为[13]
(2)
1.2.1 Bayes网络建模
通常,BN结构的建模[14]采用专家经验法和根据给定样本学习法。根据轴承故障诊断的特点,采用专家经验法。
BN参数学习是在网络拓扑结构已建立好的基础上,通过训练大量的数据,依照一定的准则学习、计算BN的参数分布。在此,采用最大似然估计算法(Maximum Likelihood Estimation,MLE)进行参数学习估算[15],可表示为
(3)
式中:e1,e2,…,em为样本集;θ为该分布的参数;fθ(ei)为其概率密度。MLE方法就是使(3)式取到最大值。
1.2.2 Bayes网络推理
肝病属于在肝脏位置发生病变的疾病,如乙肝、丙肝、甲肝、肝硬化、肝癌、脂肪化、酒精肝等,属于常见的一种较大危害性临床疾病,动物和人的胆碱酯酶包括乙酰胆碱酯酶和酰基胆碱酰基水解酶两种,乙酰胆碱酯酶大部分分布在肺、红细胞、神经末梢、脾中,也被叫真胆碱酯酶;酰基胆碱酰基水解酶主要在脑白质、心、肝、胰中分布,也被叫做假胆碱酯酶。血清胆碱酯酶是肝脏合成的一种物质[1],在损伤肝细胞时会降低合成血清胆碱酯酶的含量,减少血清中血清胆碱酯酶活性。将2013年11月—2017年11月收入的160例肝病患者和40例健康体检人员作为研究对象,报道血清胆碱酯酶检测的效果。
Bayes网络推理是利用已有BN模型,在已知证据节点集合e的取值状态下,计算非证据节点V的后验概率分布。通过现有证据可以计算各节点属于某一状态的后验概率。在此,采用运算速度快、应用成熟的联合树精确推理算法,其表达式为[14]
(4)
式中:V为所求节点变量;e为加入的证据。
2 基于小波包和BN模型的轴承故障诊断
利用小波包和BN模型的造纸机轴承故障诊断流程如图1所示。利用自行设计的特征提取函数将信号离散化后得到特征向量,然后训练BN模型参数,得到轴承故障诊断推理结果。
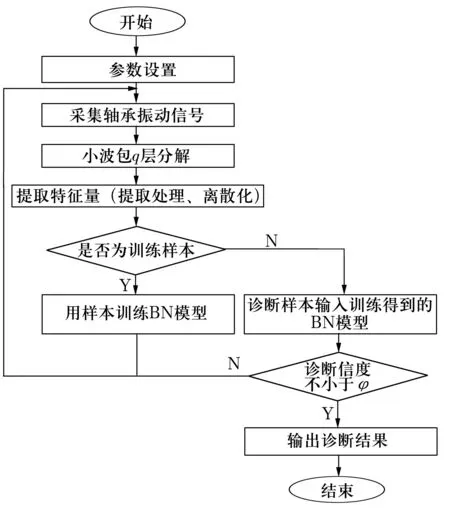
图1 诊断系统整体处理流程图
2.1 诊断数据预处理
将轴承振动信号进行小波包分解,形成初步的待诊断特征分量。为加快BN模型推理计算速度,小波包分解后还应对数据进行特征提取处理及离散化,形成最终的故障推理特征向量。
其中诊断数据的预处理主要过程为:设原始振动信号长度为N=2qrw,其中q,r,w均取正整数。按(1)式将原始信号进行q层小波包分解,可得到分量Xqj。各个频带数据量大小将变为rw。经试验验证取q=3,小波函数选用db6时,诊断效果较为理想。
2.2 特征样本获取
1)设计的特征提取函数为
(5)
式中:Xqj为初始振动信号经q层小波包分解后的第j个分量,j=1,2,…,8;w为求和个数;r为最终形成特征向量的个数;s为自然数。通过(5)式,可将每w个小波系数形成一组特征向量。
2)采用最大值离散化方法,每个分量的最大值记为Ejmax,将由(5)式得到的特征向量离散化为K个离散特征值,形成特征向量
(6)
式中:参数K取3,a取0.618。根据对应轴承振动特征信号的幅度,分别按大小离散化并量纲一化后的取值为1,2或3。
2.3 诊断模型建模与推理
BN模型结构建模采用领域专家经验得到,并通过(3)式的MLE算法学习出BN模型的参数,即概率分布函数。
联合树算法是目前BN中计算速度最快、应用最广的精确推理算法[16]。BN模型的每次推理结果分别对应了正常、内圈故障、外圈故障和滚动体故障4种轴承状态分别出现的概率,其和为1。当轴承的诊断推理概率大于所设阈值Ф,则输出诊断结果概率最大时所对应的状态;若不满足阈值判定输出条件,则继续返回采集振动信号,周而复始直至完成轴承的诊断过程。
3 试验与分析
为验证上述方法的有效性及实用性,分别采用BN模型与传统BP神经网络诊断方法进行试验分析。试验所用PC采用2 GHz处理器和2 G内存,程序通过MATLAB7.1编程完成。
3.1 试验设置
故障数据来源于SKF6205型深沟球轴承[17],试验条件为:采样频率12 kHz,电动机转速1 750 r/min,电动机负载1.491 kW,故障直径为0.177 8 mm。
参数设置:轴承原始振动信号个数N=120 064,小波包分解层数q=3,其他参数为w=32,s=2,K=3,a=0.618,诊断信度Ф=0.85。
3.2 特征向量的确定
对于每种原始状态的N个数据,进行小波包分解、特征提取、离散化处理后得到r=469组数据。选取前300组数据进行BN模型学习,后169组数据对已建立的BN模型进行验证。
按照上述预处理、特征样本获取的步骤,对原始数据X进行处理,小波包分解后记为X30~X37。限于篇幅,仅选取轴承内圈、外圈故障状态各前720个初始信号进行分析,原始信号及小波包分解信号如图2、图3所示。将图2中的小波包分解信号进行特征提取和离散化后记为D0~D7,并量纲一化为1~3,对应于轴承振动信号特征量的大小,结果如图4所示。
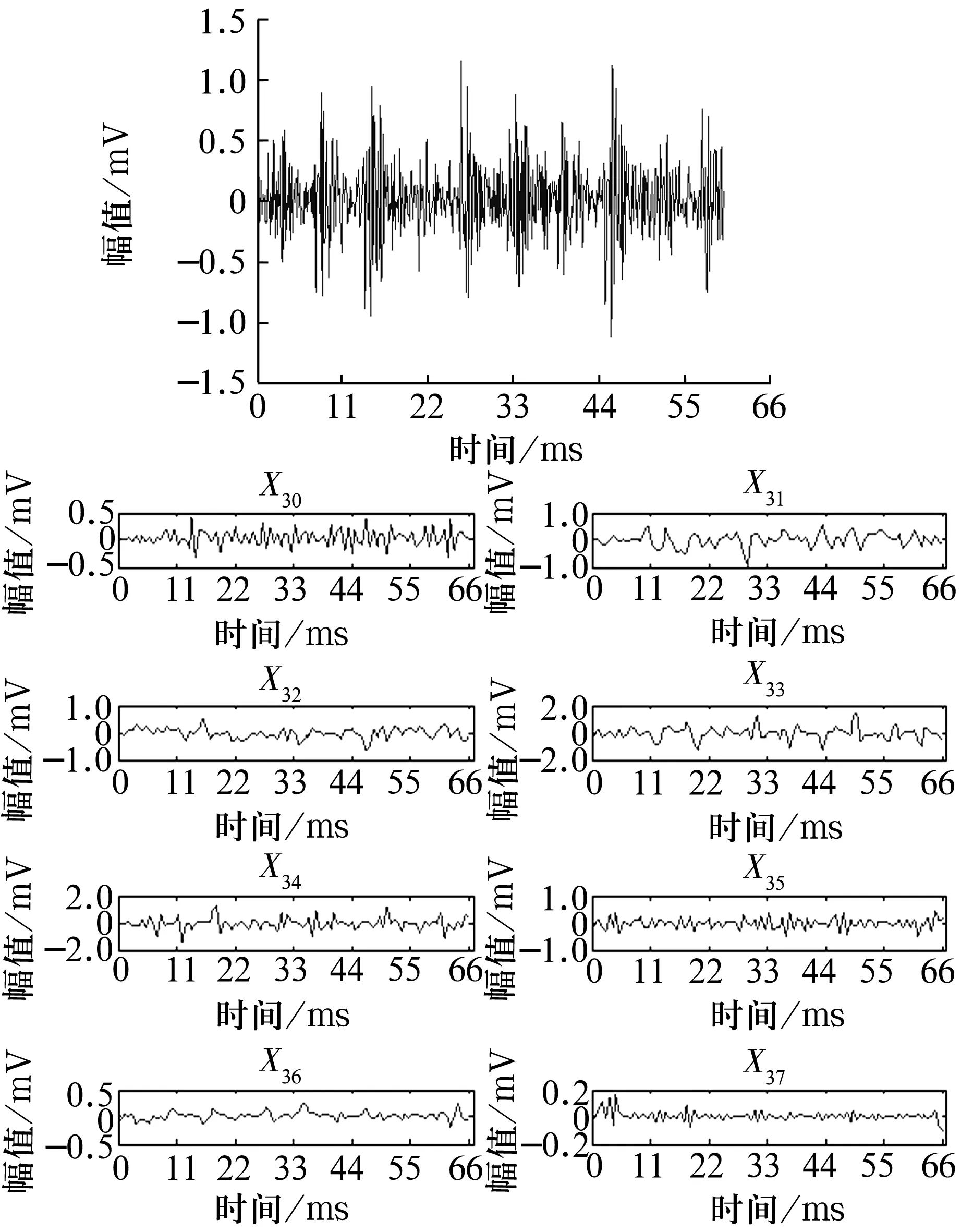
图2 内圈故障信号及其小波包分解
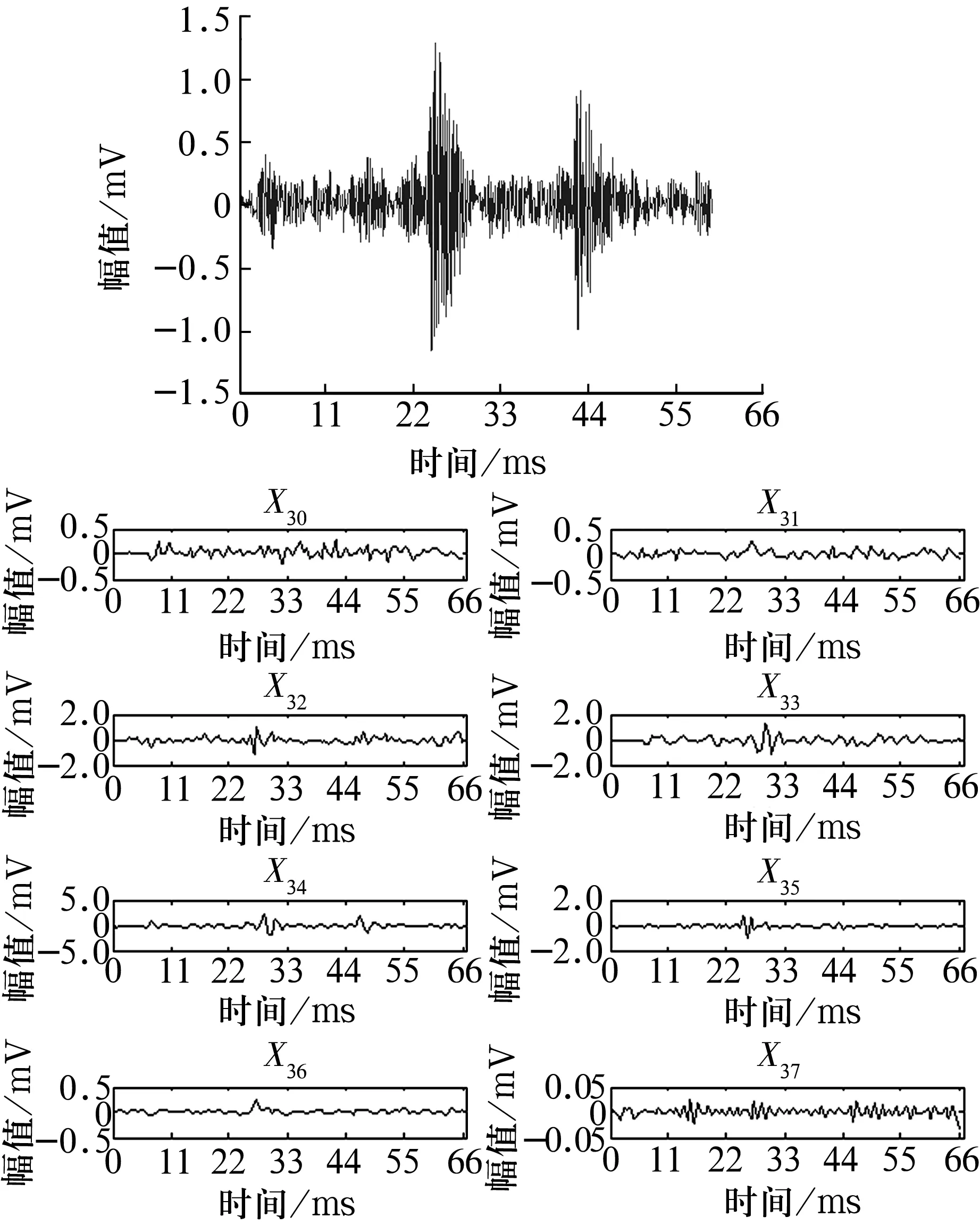
图3 外圈故障信号及其小波包分解
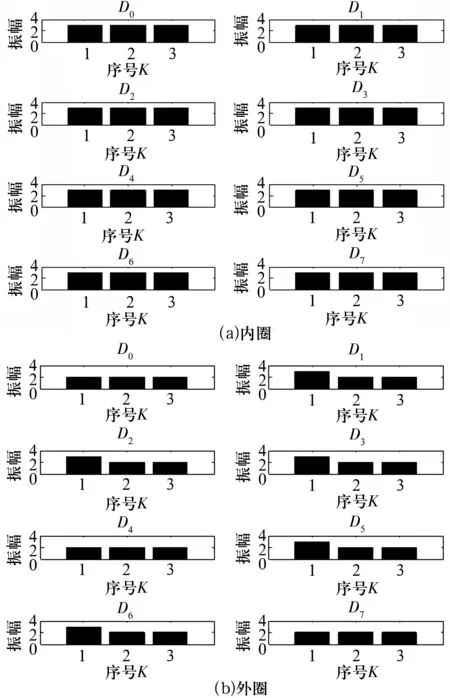
图4 离散化后的特征信号
3.3 试验模型
根据专家经验所建立的BN诊断模型如图5所示,Bearing节点代表滚动轴承所处状态,D0~D7分别代表数据处理后的8个特征向量。显然,轴承的状态信息可由8个特征向量所决定。
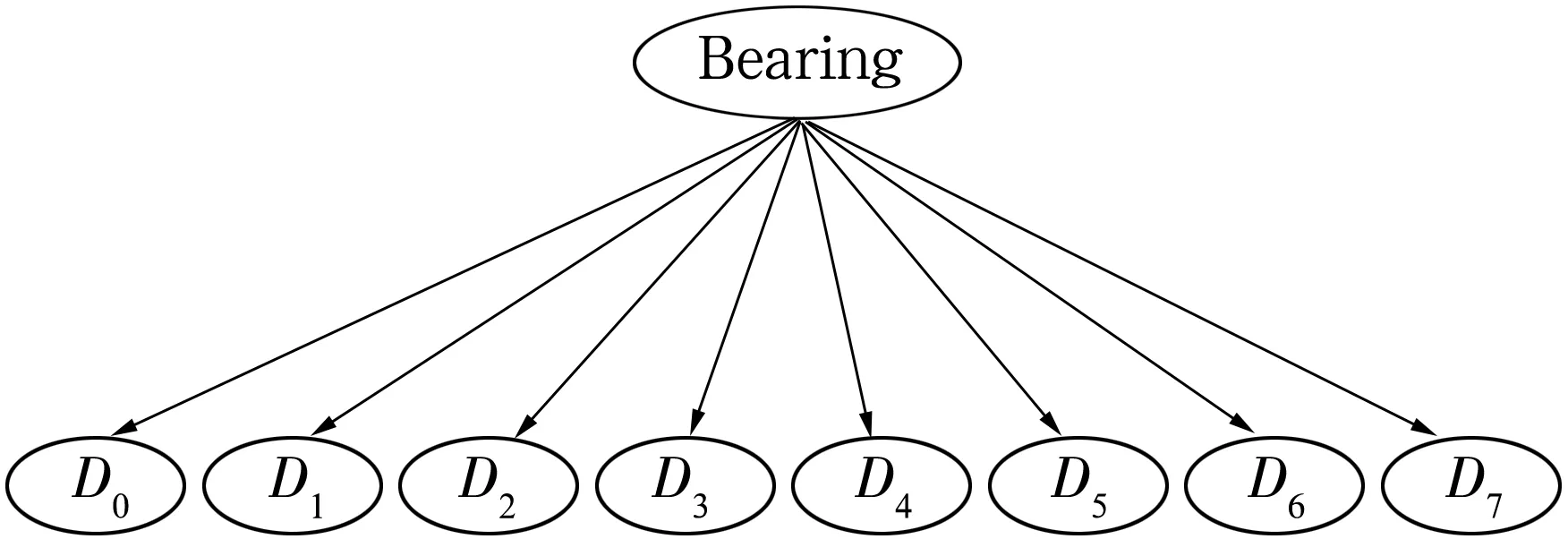
图5 BN结构建模
根据MLE学习算法得到BN网络参数,试验中的最大学习次数设为5 000。
3.4 推理过程
待诊断信号的特征向量通过离散化赋值形成用于轴承故障诊断模型的输入特征向量,利用BN模型成熟的联合树推理算法完成推理,如2.3节所述,当推理结果中状态概率大于所设诊断信度阈值Ф时,则输出诊断结果概率最大时所对应的状态,即诊断结果。
3.5 BN模型与BP神经网络的对比
为了凸显BN模型的优势,与BP神经网络进行对比分析,试验选用同样的训练样本和诊断测试样本。在进行BP神经网络诊断时,误差选用0.01,网络结构选用3层神经网路,输入层为8个神经元(对应8个特征分量),输出层为4个神经元(分别对应4种轴承状态),中间层为17个神经元,学习速率设为0.05,最大训练次数与BN相同,均取5 000次,验证诊断信度阈值也设为0.85。
3.5.1 正确率对比
当使用完全8个特征证据推理验证时,试验结果见表1。由表可知,BN模型的诊断正确率更高,效果更好。
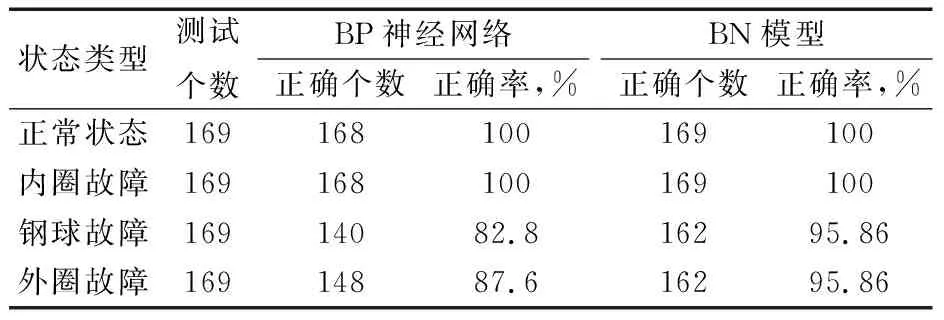
表1 完全证据下BN模型诊断结果
3.5.2 模型参数学习耗时对比
分别对BN模型、BP神经网络训练15次,模型参数学习耗时如图6所示,从图中可以看出:BN模型建模时间比较稳定,平均用时80.100 s;BP神经网络收敛速度慢,有可能陷入局部极小值,故建模时间波动较大,最短耗时11.454 s,最长耗时则高达1 751.472 s,平均用时621.885 s。所以BN模型的平均训练耗时及稳定性均优于BP神经网络。
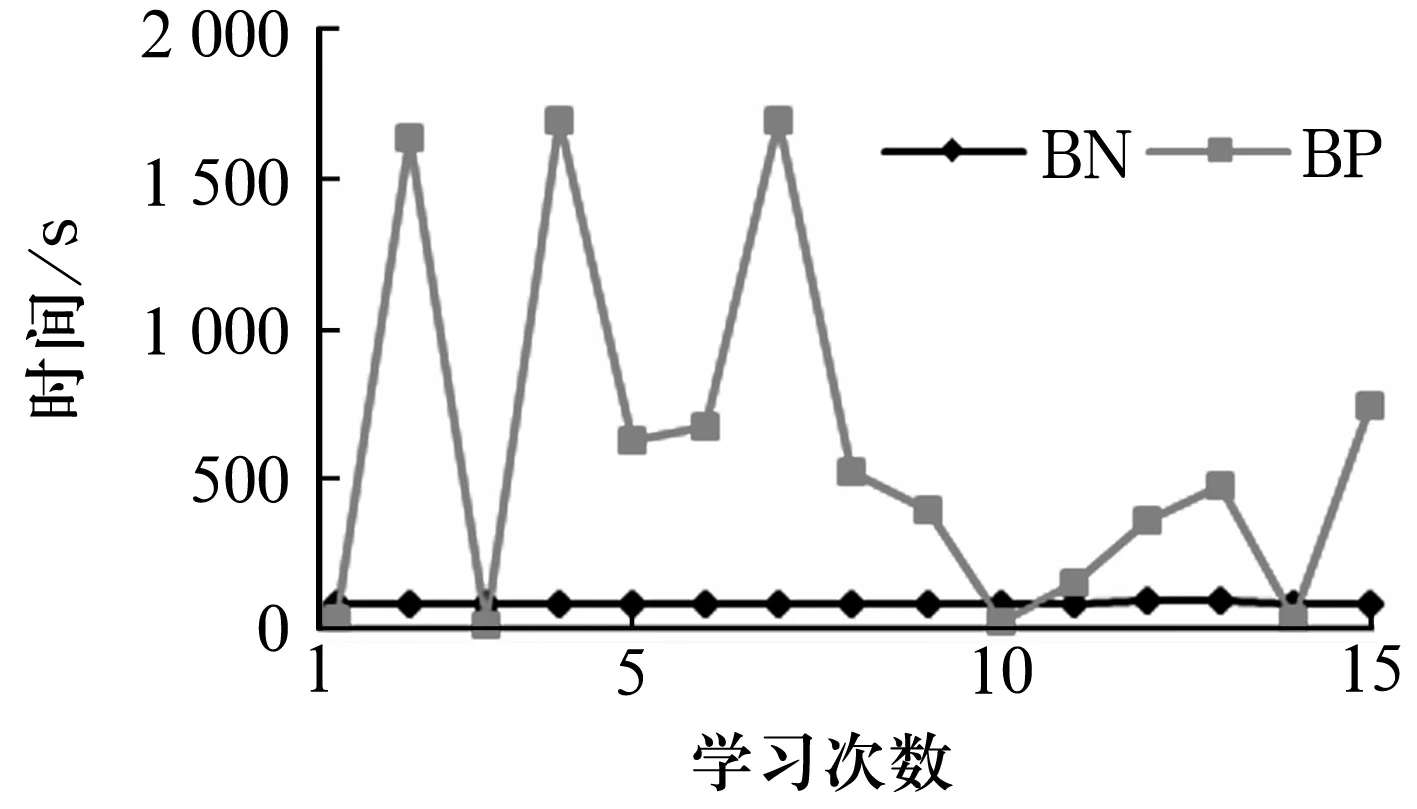
图6 BN与BP模型参数学习耗时
3.5.3 不完全证据下的推理
与BP神经网络等智能故障诊断相比,BN模型最大的优点是有能力处理输入证据不完整性的推理诊断。假设因某种不确定因素(如数据传输或网络延时)引发特征向量D4缺失时,BP神经网络没有诊断推理的能力,但利用BN模型可进行推理,其结果见表2。由表可知,BN模型对外圈故障的诊断正确率略有下降,但整体仍具有较好的推理诊断能力。
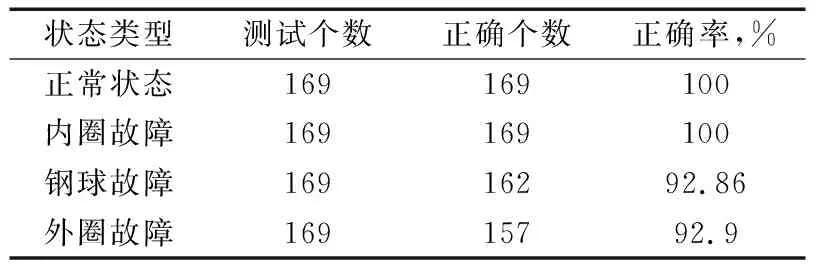
表2 不完全证据下BN模型推理结果
4 结束语
提出了基于小波包和BN模型的深沟球轴承故障诊断方法。对轴承原始振动信号进行小波包分解后,利用特征提取函数可以提取出信号在各频带上的特征信息,分别利用成熟的BN模型学习算法和推理算法,实现了造纸机用深沟球轴承故障诊断模型的建立,以及轴承运行状态的推理诊断。试验结果表明,该方法有效克服了系统中由于数据局部失效等因素造成的不确定性,能够高效识别轴承的故障状态类型,对其他机械上的轴承故障诊断也具有一定参考价值。

