常幅载荷下滑轨与滚轮寿命及可靠性研究
王浩,郭兰中,林化清,杨兰玉
(1.中国矿业大学 机电工程学院,江苏 徐州 221116; 2.常熟理工学院 机械学院,江苏 苏州 215500)
飞机襟翼收放系统中,磨损是造成系统机械故障的主要原因[1-2]。滑轨和滚轮是襟翼收放机构的重要运动副,两者之间的磨损不仅改变各自的尺寸精度,也会改变运动副间的配合尺寸以及配合精度,降低运动精度或者出现动作不协调,严重影响飞机的可靠性。当磨损超过一定限度时,就有可能影响襟翼的准确收放,造成两侧襟翼开度不一致或发生机械卡阻,危及飞行安全。因此,研究襟翼收放机构中滑轨与滚轮之间的磨损及其可靠性[3],对确定其使用寿命,制定检查周期、大修周期以及维修要求,保证飞行安全具有重要意义。大量的实践表明,在轴承与滑轨组成的运动副中,轴承的磨损失效是导致整个运动副乃至整个机构的失效的主要原因,因此将以襟翼收放系统中的轴承为中心进行研究。
1 滚动轴承磨损寿命的理论计算
磨损失效指表面之间的相对滑动摩擦导致工作表面金属不断磨损而产生失效。持续的磨损将引起轴承零件逐渐损坏,并最终导致轴承尺寸精度丧失及其他相关问题。磨损会影响形状变化,配合间隙增大及工作表面形貌变化,影响润滑剂或使其污染达到一定程度造成润滑功能完全丧失,最终使轴承丧失旋转精度乃至不能正常运转。磨损失效是各类轴承常见的失效形式之一。
滚动轴承磨损寿命是指轴承在使用过程中,随着使用时间的增加,轴承由于过量磨损而丧失正常工作性能的累计总转数,或在一定转速下的工作小时数。
由于轴承磨损规律复杂, 磨损寿命尚无完善的计算方法, 通常用径向游隙的增量来表示轴承的磨损量, 根据许用磨损系数进行估算,最终得到滚动轴承的磨损寿命计算公式为[4,5]
Lw=50(0.61lnλ+0.656)×10fv×60n,
(1)
式中:Lw为轴承磨损寿命;λ为轴承工作时的最小油膜系数;fv为轴承许用磨损系数;V为轴承的许用径向游隙增量;e0为磨损率;n为轴承转速。
2 滚动轴承磨损寿命的点估计
实践表明,大量机械设备中传动系统的失效大部分是由于滚动轴承疲劳磨损而引起的。大量试验和分析证明,寿命服从正态分布。已知分布形式,即可从样本出发,求出未知参数的估计。
参数估计可分为点估计和区间估计,现采用点估计,即总体ξ分布的形式已知,分布参数θ1,θ2,…,θm(如正态分布的均值和标准差)未知,从样本(X1,X2,…,Xn)出发,求出m个统计量,作为未知参数θ1,θ2,…,θm的估计[6]。
正态分布均值的点估计为
(2)
标准差的点估计为
(3)
在指定可靠度R下,可靠寿命的点估计为
(4)
式中:ZR按可靠度R查表1确定。

表1 ZR与可靠度R的关系[8]
3 试验
3.1 试验设备及试样
试验设备为自制的往复式多用途摩擦磨损试验机,示意图如图1所示。整个装置固定在立柱、压梁和平台组成的承力框架中,通过丝杠和压力传感器给固定摩擦副的上磨板和车式下磨板施加径向载荷Fr,联体式电磁可调电动机通过连杆机构使下磨板做往复运动。该试验机可一次同时安装4套轴承及2个与之配对的滑轨(图2),不仅可以提高试验效率,也可保证试验条件的一致性,从而有效地减小试验误差,提高试验数据的可靠性。

图1 试验设备原理图

1—滑轨1;2—轴承1;3—轴承2;4—轴承4;5—轴承3;6—滑轨2
为使试验结果尽可能符合实际情况,上磨块为36102轴承,材料为GCr15,宽度B=9 mm,内径d=15 mm,外径D=32 mm,接触角α=15°,额定动载荷Cr=4.5 kN。下磨块(滑轨)材料为40CrNiMoA,结构尺寸如图3所示。

图3 下磨块结构尺寸图
3.2 试验方法
文献[8-9]在进行寿命试验时,观察到存在不失效寿命。所以,考虑到滚动轴承在试验中可能出现无限寿命的情况,即存在一个极限载荷,低于该载荷,轴承便不会产生疲劳破坏,滚动疲劳磨损试验设计为常幅定数截尾试验,即当4套滚动轴承试样中有3套失效即停止试验。试验示意图如图4所示。
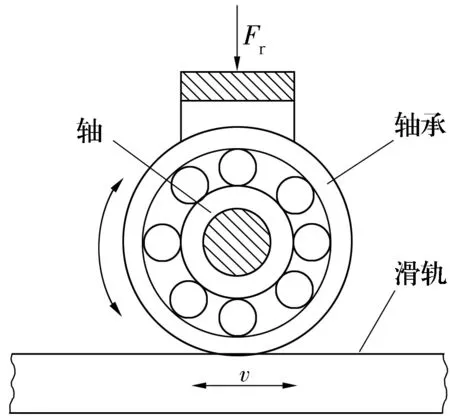
图4 试验示意图Fig.4 Diagram of test
试验时,加载装置通过上磨板施加4 000 N的径向载荷,由于结构尺寸的对称性,每套轴承承受1 000 N的径向载荷。载荷通过压力传感器以及与其相连接的标准载荷测量仪(准确度<0.005%FS,温度系数<5×106,A/D转换速率>50次/s)控制。通过联体式电磁可调电动机控制转速,调速范围为200~1 400 r/min,转速比i=80,输出的转速为2.5~17.5 r/min,试验时转速为7 r/min。试验部件的力学性能见表2。

表2 部件材料的力学性能
轴承失效的判定:在试验过程中,当轴承出现旋转精度降低,最终无法正常工作时,视为该轴承磨损失效。
采用外圆千分尺测量轴承的磨损量,即为原始尺寸与相互垂直的2个直径方向上测量值的平均值之差;采用深度千分尺测量滑轨的磨损量,取整个磨损表面均匀分布的9个测点测量值的平均值。
3.3 结果与分析
轴承失效时的循环次数见表3,其磨损量与寿命曲线如图5所示。由于试验机一次循环轴承滚动距离为520 mm,而轴承外径为32 mm,通过计算可得,一个循环即曲柄旋转一周,轴承转数为5.18 r。滑轨的磨损量与寿命曲线如图6所示。轴承和滑轨平均磨损量对比如图7所示。

图5 轴承磨损量与寿命曲线

图6 滑轨磨损量与寿命曲线

图7 轴承与滑轨平均磨损量对比
由表3可知,当循环次数达到43 965次(轴承转数为227 739 r)时,有3套轴承失效。因此可初步认为,在相同工作条件下,36102轴承的可靠工作寿命不会超过227 739 r。

表3 滚动轴承失效时的循环次数
由图5和图7可知,轴承磨损量拟合曲线的左端延长线距离坐标原点很近,说明该轴承在投入工作后,基本没有磨合期,一开始就处于比较稳定的磨损状态,且磨损量的拟合曲线斜率很小,表明在相同循环次数下增加的磨损量比滑轨小。这是由于航空滚动轴承的尺寸精度、形状精度和表面质量均较高。
由图6和图7可知,滑轨存在比较明显的磨合期,范围大致在3 000次循环,此时磨损量达到0.015 mm,然后稳定增加,但磨损量拟合曲线初始阶段斜率较大,表明在相同循环次数下增加的磨损量比滚动轴承大。
由此可知,在滚动轴承与滑轨组成的摩擦副中,滑轨磨损量比轴承大。
4 滚动轴承理论磨损寿命和试验寿命对比分析
已知:根据轴承的应用经验,将该轴承的许用径向游隙增量定为径向游隙的20%,该轴承接触角为15°,径向游隙为13.9 μm,即增量V为2.78 μm,磨损率e0取为1.2 μm,这样该轴承许用磨损系数fv取值约2.316 ,又经计算,轴承工作时最小油膜系数λ=6.77,代入(1)式可得轴承寿命Lw=5.05×106r。

比较轴承理论寿命(5.05×106r)和根据试验数据计算的寿命点估计(2.10×105r)可知,前者是后者的24倍。轴承寿命非常离散,一批结构、材料、热处理、加工方法均相同的轴承在相同工况下,其最高和最低寿命有可能相差几十倍甚至更多[4,10],原因为:
1)滚动轴承磨损寿命计算方程都是建立在大量试验基础上的。试验时轴承内圈相对于轴、外圈相对于轴承座无相对运动,仅内、外圈之间通过钢球发生相对运动,且通过润滑系统进行润滑[11],并通过调整润滑油流速控制试验温度。而本试验在室温下进行,除了内、外圈的相对运动以外,外圈对于滑轨有相对运动,且采用油脂润滑,无法对试验温度进行严格控制,运动形式和工作环境较为复杂。
2)在滚动轴承磨损寿命计算方程中,V,e0,fv,λ对计算结果影响大。在计算过程中,λ与e0可以通过一定的估算得到,而径向游隙的增量V则定为径向游隙的20%,该值是根据应用经验得出,可能存在一定的误差。若要使滚动轴承磨损寿命计算方程的计算结果与实际相吻合,可对V,λ,e0的取值问题进行更进一步的深入研究,并给出具有可操作性的取值原则。
由于影响滚动轴承寿命的因素复杂,磨损寿命理论仍需进一步完善。本试验属于模拟台架试验,由于样本较少,基于正态分布的可靠寿命点估计的误差不容忽视,但4套轴承中有3套均在2×105r以后失效,可以认为通过试验确定的寿命的点估计是可信的,同时也说明理论计算公式还存在一定缺陷。
5 结束语
通过试验研究了常幅载荷下滚动轴承与滑轨的疲劳磨损行为,并采用滚动轴承磨损寿命计算方程计算其理论寿命,同时根据试验数据,对给定可靠度为0.99时的轴承寿命进行了估计。由试验结果可知,高精度滚动轴承磨损量基本随时间呈线性关系,没有明显的磨合阶段;而滑轨则存在明显磨合阶段。这是由二者精度和表面质量不同所致。轴承理论寿命和根据试验数据计算的寿命的点估计存在较大差异,这是由系数V,λ,e0取值的模糊性造成的。

