高温超导轴向磁悬浮轴承的悬浮力分析

刘飞，裴旷怡，孔奎，张钢，孟庆栋

(上海大学 机电工程与自动化学院，上海 200072)

超导磁悬浮系统由超导体(HTS)、永磁体(PM)和冷却系统组成，主要应用在超导磁悬浮轴承[1-2]、飞轮储能系统[3-4]、磁悬浮导轨列车[5-6]、陀螺导航等领域。随着各种交叉学科、高新技术的发展，国内外对高温超导磁悬浮轴承试验及理论研究也越来越广泛深入。高温超导磁悬浮轴承(SMB)分为径向和轴向2种类型[7-10]。文献[11]通过对杨氏模型和Hull John R模型进行改进，提出一种改进的磁通冻结-镜像模型，其虽然考虑了磁滞模型，也可以适用径向和轴向的超导磁悬浮轴承且方法简单，但只能对超导轴承进行定性分析，不能对磁偶极子进行精确计算。文献[12]在超导计算中加入了超导的各向异性，给出了临界电流密度与各向异性的关系，利用T方法对超导悬浮力展开了数值计算，并对不同运动状况下的悬浮力进行了分析。文献[13-14]基于A-V方法，采用控制体积法对高温超导磁悬浮系统的悬浮力和导向力进行了数值计算，经验证计算结果与试验结果比较接近。下文介绍一种基于磁矢势的悬浮力计算方法，对轴向高温超导磁悬浮系统展开力学分析，并与已有试验结果进行比较。

1 数学计算

1.1 基于分子电流法求解磁场强度

分子电流法是基于对永磁环表面等效电流的分析建立的数学模型，即假设永磁体内部没有电流，其磁动势可用等效的表面电流表达。轴向磁化的永磁环的等效电流模型如图1所示。

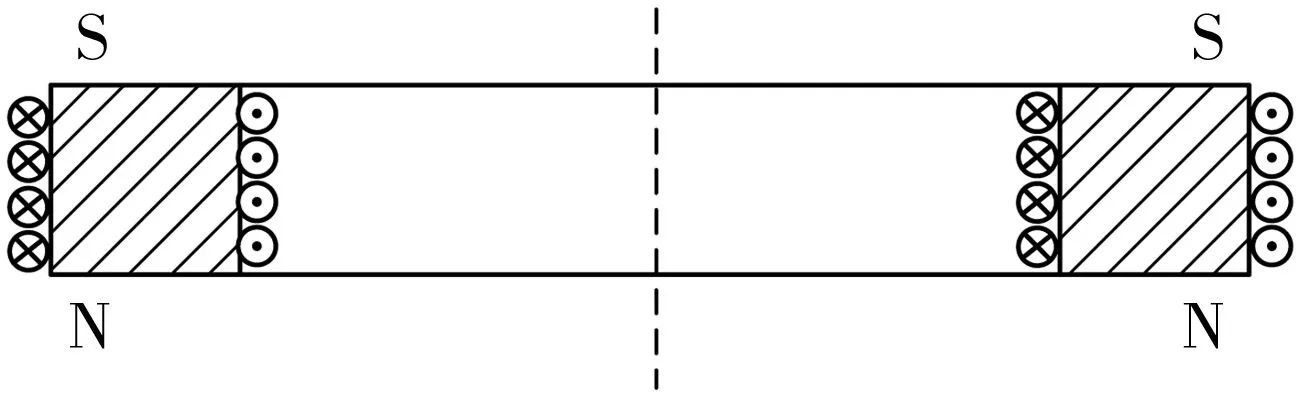
图1 轴向磁化永磁环的分子电流模型

根据Biot-Savart定律，电流元在空间产生的磁感应强度为

(1)

式中：dB为电流元产生的磁感应强度；μ0为真空磁导率；i为环形导线中的电流；dl为电流元长度；r为电流元矢径。

利用Biot-Savart定律对永磁体的磁感应强度Br求解，通过磁场强度求解出永磁体在空间的磁场分布情况。建立柱坐标系(ρ,φ,z)如图2所示，对于无限长柱形永磁体，其磁感应强度可表示为

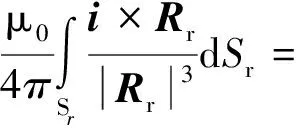
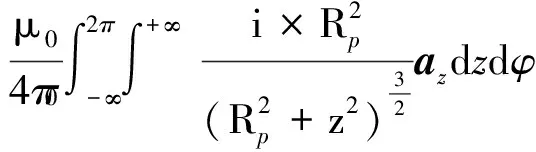
(2)

式中：Sr为柱形永磁体外表面面积；Rp为柱形永磁体的外半径；az为沿z轴方向的单位矢量。

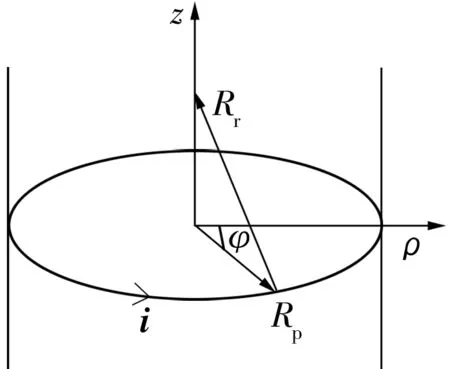
图2 无限长圆柱永磁体

高温超导磁悬浮轴承中的永磁转子多采用环形永磁体，计算永磁环在空间磁场分布，即计算2个柱形永磁体计算的矢量和。为便于计算，建立如图3所示的柱坐标系(ρ,φ,z)，点P(ρ,φ,z)为空间内任意一点，P′(ρ′,φ′,z′)为永磁体面上任意一点。通过对单个电流元积分，可得柱形永磁体在空间任意一点P的磁矢势为

(3)

r-r′=(ρ-ρ′cosφ″)aρ+

(ρ′sinφ″)aφ+(z-z′)az，

φ″=φ-φ′，

式中：aρ为沿半径ρ方向的单位矢量；aφ为沿偏移角度方向φ的单位矢量。

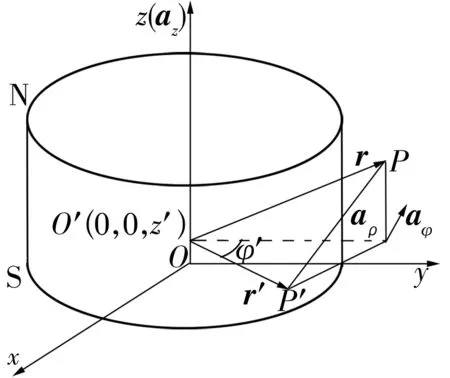
图3 永磁体磁场分布模型

由 (2) 式和(3)式可得外径为Rp、厚度为tp的柱形永磁体在P点的磁矢势为

。(4)

环形永磁体的磁矢势可等效为求解外半径为Rp柱形永磁体的磁矢势AR(ρ,z)和内半径为rp柱形永磁体的磁矢势Ar(ρ,z) 的矢量和，即

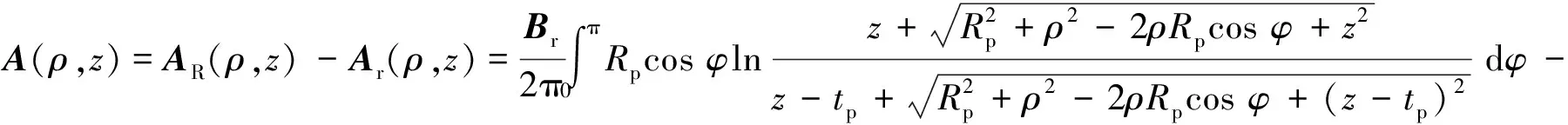
。(5)

上式为定积分表达式，由于被积函数比较复杂，可以通过积分的近似数值求解

(6)

式中：Ak(k=0,1,2,…,n) 为求积系数，与函数f(xk)无关；ζk,xk为积分变量。

根据以上原理对柱形永磁体的磁矢势求解。首先进行变量变换，将φ的积分分成μ1，μ2，μ3，…，μM，变换形式为

φ′(ui)=πui-sin πui，

(7)

则dφ′(ui)=π-πcos πui。

将 (7) 式代入 (5) 式可得

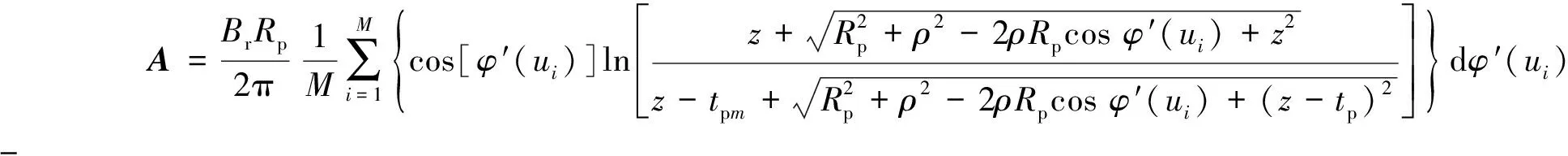
(8)

式中：tpm(m=1,2,3，…,M)为将柱形永磁体分解成M个部分后每个磁体的厚度。

在坐标系中，对磁矢势A求旋度，可得磁感应强度B为

(9)

由 (3) 式可知磁矢势的方向与环形电流的方向相同，因此柱形永磁体产生的径向磁感应强度为

(10)

式中：F，E分别为第一类、第二类完全椭圆积分。

柱形永磁体产生的轴向磁感应强度为

。(11)

永磁环的磁感应强度为半径Rp和rp的柱形永磁体磁感应强度的矢量和。在高温超导磁悬浮系统中，永磁转子多为永磁环的叠加。不同的叠加方式产生的磁感应强度分布如图4所示。图4a表明磁环轴向叠加的径向磁悬浮轴承转子产生的径向磁感应强度呈对称分布；图4b表明磁环径向叠加的轴向磁悬浮轴承转子产生的轴向磁感应强度则呈不规则连续分布，在磁极外半径处磁感应强度达到最大值。

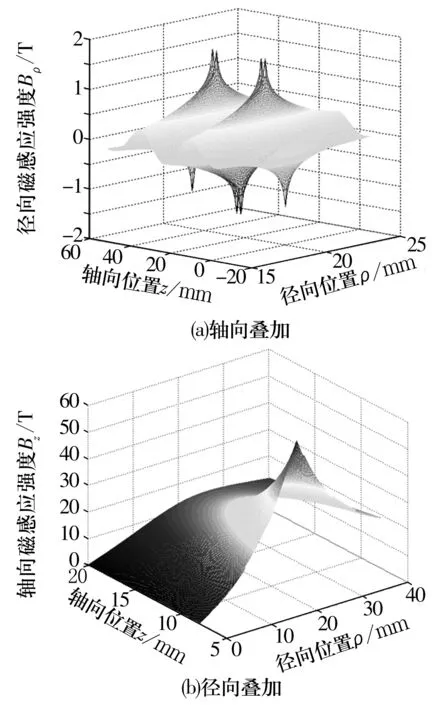
图4 不同的叠加方式产生的磁感应强度

1.2 悬浮力的计算

由Faraday电磁感应定律可知，当磁场变化时导体内产生涡流现象。在超导体内部任意一点的磁矢势为永磁体产生的磁场Ap和超导体内电流产生的磁场As的矢量和，即

A=Ap+As。

(12)

根据Biot-Savart定律，超导体内电流产生的磁矢势为

(13)

式中：rs，Rs分别为超导体的内、外半径；ts为超导体厚度；Js为超导体内的电流密度。

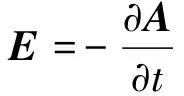
(14)

E-J幂指数关系模型[1]为

(15)

式中：Ec为超导体中的临界场强；J为电流密度；Jc为温度T下的临界电流密度。

将 (15) 式代入 (14) 式可得

(16)

结合 (8)，(12)，(13)和(16) 式可得

(17)

选取的高温超导体为块状钇钡铜氧，该材料中的电流密度有很强的各向异性。为此，将超导块沿厚度方向划分为Nz个平行薄片，只考虑氧化铜内的屏蔽电流。为了便于计算，在每一薄片内再进行网格划分，如图5所示，分别从径向和圆周方向将薄片等分为Nρ×Nφ个。求解过程中假设每个网格内的电导率是恒定值。对于涉及时间域的电磁计算，选取等长的时间跨度dt，对 (17) 式三重积分的求解转化为

(18)

式中：ΔV为网格的体积。

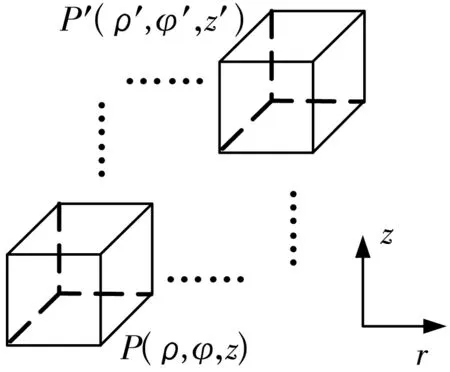
图5 超导体网格划分

由(17) 式求出超导体内的电流密度后，根据洛伦兹力可求得高温超导磁悬浮系统的悬浮力为

(19)

具体计算流程如图6所示。

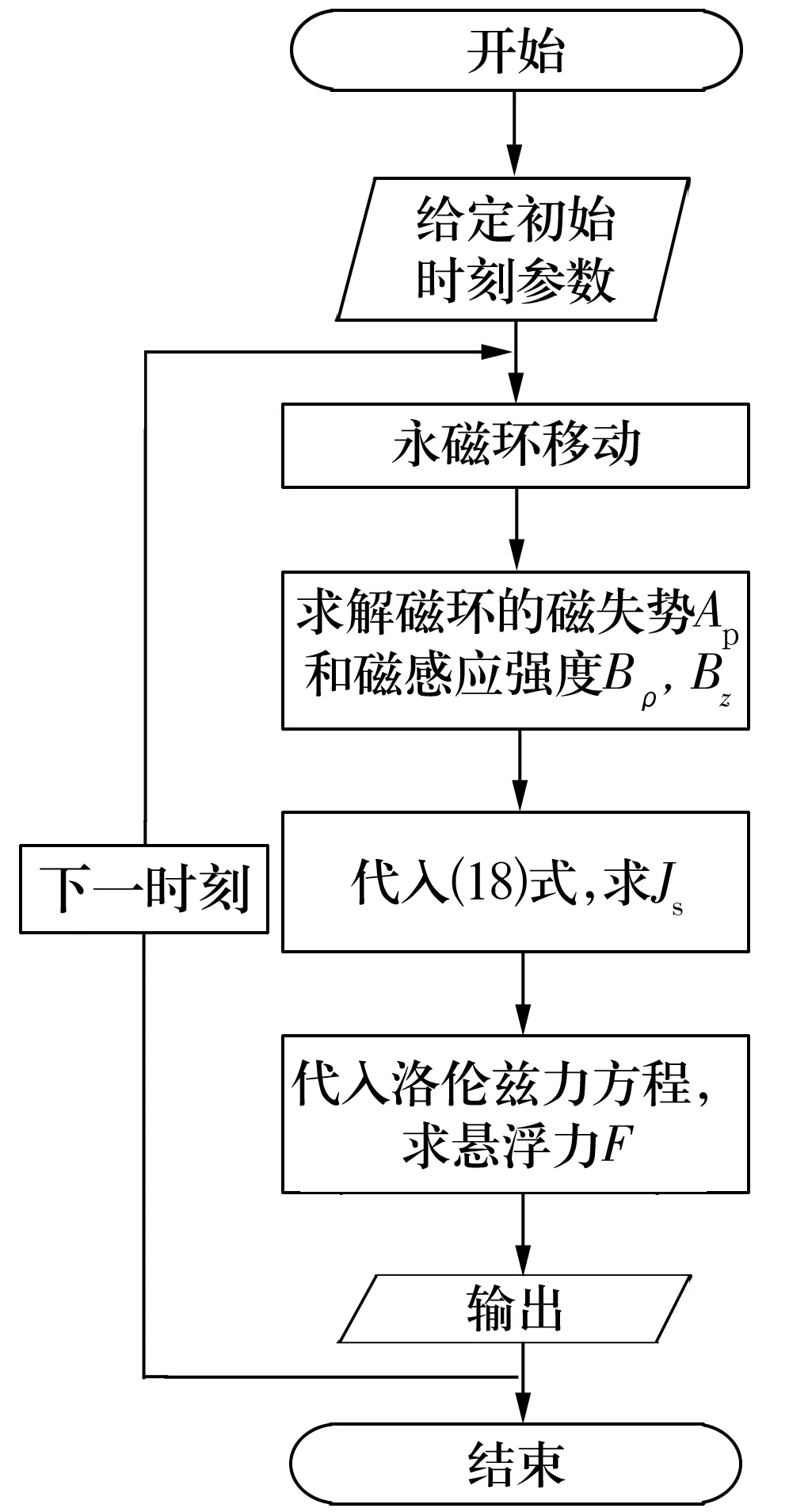
图6 悬浮力计算流程

2 超导轴向磁悬浮轴承悬浮力性能分析

对于轴向超导磁悬浮轴承，一般永磁体位于超导体的上方，如图7所示。若永磁体受到轴向的扰动力Fz而产生轴向位移z，则超导体会给予永磁体反作用力Fsz阻止其运动。

图7 轴向高温超导磁悬浮的轴向移动

2.1 场冷高度40 mm(零场冷)

为便于与其他计算和试验结果[14-15]作比较以校正模型的正确性，选取与文献中相同的柱形超导体：半径Rs=10.5 mm，厚度ts=10 mm，临界电场Ec=1，临界电流密度Jc=1×108A/m2，指数n=20；永磁体半径Rp=11 mm；厚度tp=20 mm，剩磁强度Br=1.1 T。

假设永磁体在距离超导体上表面40 mm位置开始冷却，冷却后施加向下的Fz使永磁体以1 mm/s的速度下降到距离超导体上表面3 mm处，再施加反向Fz使永磁体以1 mm/s的速度向上移动到40 mm处。永磁体往复运动中受到超导定子的反向作用力Fsz。场冷高度40 mm下轴向力随轴向位移的变化如图8所示。由图可知：永磁体上升过程中，理论计算值与文献[14-15]中的试验值吻合度较高，在3 mm处的最大值比试验值小0.7 N左右；永磁体下降过程中，二者差别较大。这是因为当永磁体与超导体之间的间距最小时，超导体所处的磁场强度最大，有大量磁通穿入超导体内；当永磁体与超导体的间距逐渐增大时，超导体所处的外部磁场强度减小，使得穿入超导体的部分磁通被排出，但由于磁通钉扎作用，产生了磁滞现象，此时超导体内部磁通运动较为复杂，文中采用的E-J模型虽然可以给出磁通运动的本质规律，但由于进行了大量简化，因此当磁通运动剧烈时模拟结果存在误差。

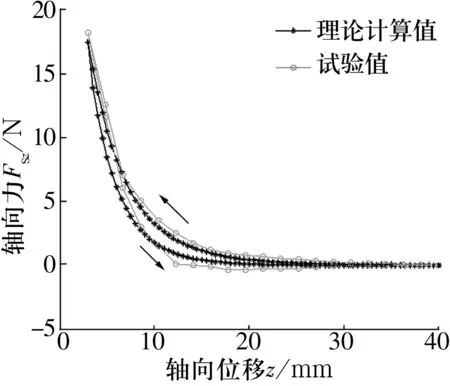
图8 场冷高度40 mm下轴向力随轴向位移的变化

2.2 场冷高度1 mm

选取与文献[16]中相同的试验参数：高温超导体直径为30 mm，高度为12 mm，临界电流密度为Jc=100 A/cm2；永磁体的直径和高度均为12.7 mm，剩磁强度为0.831 T。

将高温超导体在场冷高度为1 mm处进行冷却，在足够的永磁体产生的外磁场强度条件下，高温超导体由正常态转变成超导态。同样施加Fz以1 mm/s的速度上升到距离高温超导体上表面25 mm处，再返回初始位置。场冷高度1 mm下轴向力随轴向位移的变化如图9所示。

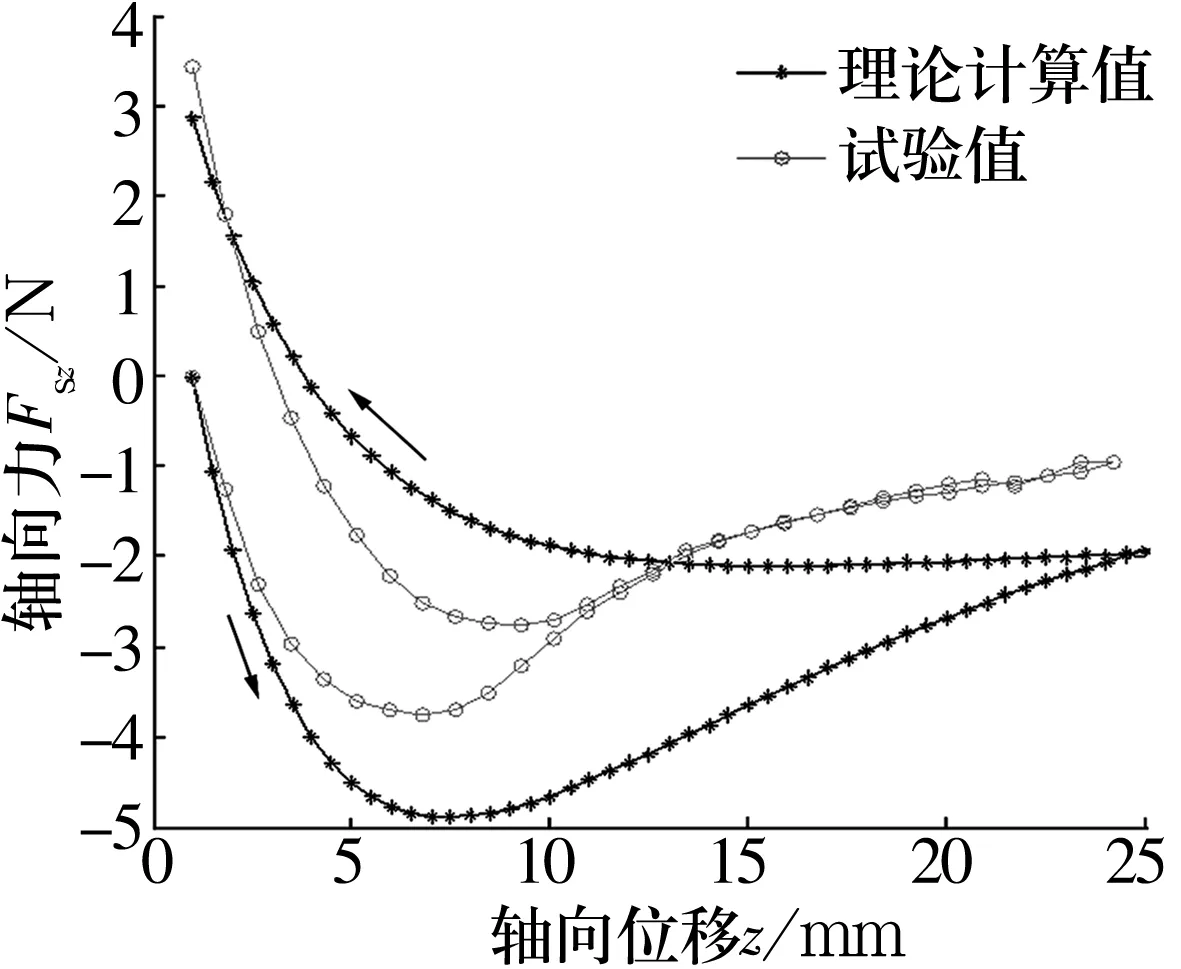
图9 场冷高度1 mm下轴向力随轴向位移的变化

由图9可知：永磁体开始上升时，理论计算值与试验值基本吻合，随着轴向位移的增大，二者的差值增大，直至轴向力最小(轴向位移8 mm)时误差为1 N；永磁体下降过程中，理论计算值和试验结果的最大误差约为2 N。这是因为在场冷过程中，部分磁通被钉扎在超导体内(即冻结磁通)，其与永磁体的相互作用使永磁体受到的悬浮力与零场冷却下的悬浮力不同。另外，选取的E-J关系模型与实际有所差距，运动时间的增加会使温度发生变化从而影响计算结果。

2.3 小结

通过对比2种不同场冷高度下的理论计算结果与试验结果可知：文中计算方法对零场冷却下和场冷却下悬浮力(轴向力)的分析均适用。在零场冷却下悬浮力几乎均为正值，超导体主要表现抗磁特性；场冷却下悬浮力为负值，先快速增大后逐渐减小，由于超导体俘获的磁通较多，主要表现出磁通钉扎特性，使得永磁体和超导体之间的磁力较大。由此可知，初始冷却条件对悬浮力的影响显著，可以通过调整初始冷却条件实现对悬浮力的控制。

3 结束语

对永磁环的磁场分布情况进行了分析，列出了高温超导磁悬浮力计算方法和流程，利用该方法对不同冷却方式下轴向高温超导磁悬浮系统的悬浮力进行了计算。对比试验结果可知，该方法在永磁体轴向时对轴向力计算是可靠的。在轴对称情况下，永磁体在超导体上方轴向移动过程中受到反作用力；超导体在零场下冷却时产生的轴向悬浮力比场冷却下的大，且磁滞特性不明显。