调心滚子轴承滚子与滚道密合度最佳设计

孙东，贾现召,罗天宇，范卫锋

(1.河南科技大学 机电工程学院，河南 洛阳 471039;2.洛阳轴研科技股份有限公司，河南 洛阳 471039)

调心滚子轴承滚子与滚道的密合度λ是轴承设计过程中的一个重要参数，实际设计中通常依据经验取λ=0.97～0.98[1-3]。至于为何如此选择，则鲜有报道。文献[1]讨论了球面滚子端部与滚道之间是否存在应力集中的问题，认为当接触椭圆长轴2a与滚子长度l满足2a1.5l时将产生端部应力集中。然而数值计算表明，条件l≤2a<1.5l过于宽泛，此时滚子端部已存在明显的应力集中。由于其涉及Hertz接触应力与变形计算，因此与密合度间接相关。下文将针对这一问题进行探讨，并给出密合度的最佳设计。

1 密合度

调心滚子轴承滚子与滚道的密合度为

(1)

式中：rw为滚子球面半径；R为滚道圆弧半径。

滚子与滚道的接触如图1所示。

图1 滚子与滚道接触

2 密合度最佳设计

初始状态下，滚子有效长度端点与滚道之间的间隙为

S=Sw-SR，

(2)

式中：le为滚子有效长度；Sw为滚子端部与接触平面(虚线)之间的距离；SR为与滚子端点对应的圆弧滚道与接触平面之间的距离。

由(1)，(2)式得

(3)

在载荷作用下，滚子将产生径向压缩位移δ。当δS时，滚子端部将产生应力集中。最佳情况为δ等于或略大于S，如图2所示，此时接触椭圆的长轴等于或略大于滚子有效长度，既能实现滚子全长承载，又不产生或只产生轻微的端部应力集中。

图2 接触位移与接触椭圆

对于线接触滚子的压缩位移，在钢-钢接触情况下，由文献[4]可知

(4)

当δ=S时，由(3)和(4)式得

(5)

由(1)和(5)式可确定最佳密合度和滚子球面半径。由(5)式可知，滚子最佳球面半径与滚子载荷相关，即若能确定轴承载荷，则可以有针对性地进行最佳应用设计(个性化设计)。但滚动轴承作为一种通用机械基础零件，应用环境千差万别，不可能事先只针对某一种载荷进行设计。为解决该矛盾，通常将与载荷有关的几何参数，如密合度、凸度等与某个特定的载荷(如轴承额定动载荷)联系起来。

如图3所示，当轴承承受径向载荷Fr时，滚子的最大载荷为[5]

图3 调心滚子轴承

(6)

式中：Z为单列轴承的滚子数量；α为接触角；Cr为额定动载荷；κ为设计载荷系数，κ=0.1～0.2，表示中等载荷至重载荷。

3 实例分析

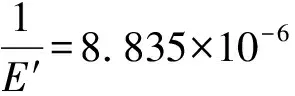
将已知参数代入(1)，(5)，(6)式，计算得：Q=6 030 N，λ=0.975，rw=81.9 mm。

由Hertz点接触公式计算接触椭圆的长轴，根据文献[6]的方法，最终计算得接触椭圆长轴2a=17.27 mm。可以看出，接触椭圆的长轴只比滚子有效长度长约5%。根据文献[6]中有限长线接触问题数值计算方法,对该例进行了数值计算，最大接触应力沿滚子长度的分布如图4所示。由图可知，滚子端部只有轻微的应力集中，说明密合度取值合理。

图4 滚子最大接触应力分布