时栅位移传感器的动态特性研究

杨继森　张　静　江中伟　李小雨

重庆理工大学机械检测技术与装备教育部工程研究中心，重庆，400054



时栅位移传感器的动态特性研究

杨继森张静江中伟李小雨

重庆理工大学机械检测技术与装备教育部工程研究中心，重庆，400054

摘要：为了解决时栅角位移传感器的动态测量问题，在基于静态的时栅位移传感器电磁仿真的基础上，通过引入运动单元模块，建立了时栅位移传感器的动态电磁仿真模型。通过分析时栅位移传感器的感应电动势幅值信号和感应频率信号，得到了动态条件下的时栅位移传感器感应电动势幅值和频率与转子转速的关系，并测算了磁场式时栅位移传感器在激励频率为400 Hz的情况下，理论上能够达到的极限转速为8 r/min。实验结果表明，转子转速在0～8 r/min时传感器动态误差为±1.4″,速度超过8 r/min时传感器精度开始恶化，转子转速为10 r/min时传感器误差为±8.2″。

关键词：时栅位移传感器；动态仿真；感应电动势；转子转速

0引言

时栅角位移传感器是一种新型的电磁感应式传感器，以时空坐标转换理论(即TST理论)作为测量的理论基础[1]，采用类似三相感应电机的结构，利用机械加工、绕线的方式构成传感器的传感基体[1]。目前，时栅角位移传感器的静态测量精度达到±0.8″，在测量仪器、数显转台等行业得到广泛应用。随着时栅角位移传感器应用范围的不断拓展，传感器动态测量问题得到越来越多的关注。Ansoft Maxwell作为电磁有限元仿真中常用工具软件，被大量运用于工程实际中电磁仿真领域，其求解算法建立在基于Maxwell微分方程的基础上，同时采用有限元的离散方法将实际电磁场计算转换为矩阵的求解[2]。武亮等[3]通过Ansoft仿真软件对磁导调制型时栅位移传感器的定子与转子的齿宽比和定子齿槽数进行了优化，发现当定子与转子齿宽比为1∶2时，驻波包络线基波幅值最大；磁导型时栅位移传感器的定子最佳齿宽为1～2 mm。汤其富等[4-6]对时栅位移传感器进行了研究，通过对时栅位移传感器的结构仿真，结合一种锁定方法器，解决了时栅位移传感器转子转动对动测头的影响，进而导致传感器精度下降的问题[4]；通过对磁导调制型时栅位移传感器的静态仿真，优化了传感器合成的磁行波的非标准正弦形式，并通过仿真与实践的结合验证了该类传感器结构具有抑制驻波信号共模干扰的作用[5]；通过对时栅位移传感器的电磁仿真验证了时栅位移传感器中存在的多普勒效应[6]，但是对传感器转子转速与传感器感应电动势幅值之间的关系没有明确量化，也没有对多普勒效应对传感器感应电动势的影响程度进行量化。刘小康等[7]通过Ansoft仿真软件对纳米时栅位移传感器的动极板与定极板之间的间距进行优化，同时结合试验对传感器结构参数进行了验证。在对时栅位移传感器进行电磁仿真时，若设置的转速太大，则不符合时栅位移传感器的实际情况。高忠华等[8]通过定角平移自标定方法对时栅位移传感器的静态误差进行了自标定，但没有涉及时栅传感器动态误差测量问题。

综上分析，目前对时栅位移传感器开展的电磁仿真研究主要集中在静态仿真，而对时栅位移传感器的动态电磁仿真研究较少，部分涉及传感器的动态仿真的研究只进行了简单的实验验证，没有进行量化处理，或者设定的转速过大不符合时栅位移传感器的实际情况。基于此，本文提出了磁场式时栅位移传感器的动态电磁仿真，设定的转子转速完全符合时栅的实际应用要求，同时定量分析时栅位移传感器转子转速与感应电动势幅值以及频率之间的关系，以期找到影响时栅位移传感器动态测量精度的因素。

1磁场式时栅位移传感器工作原理

磁场式时栅位移传感器在原理上采用“时间测量空间”的新型测量理论，其核心就是构建一套相对匀速的坐标系，其中质点因运动引起的位置差可表现为另一套坐标系中的时间差[9]；在结构上通过引入“场”的自然属性而采用类似三相感应电机结构，如图1所示。

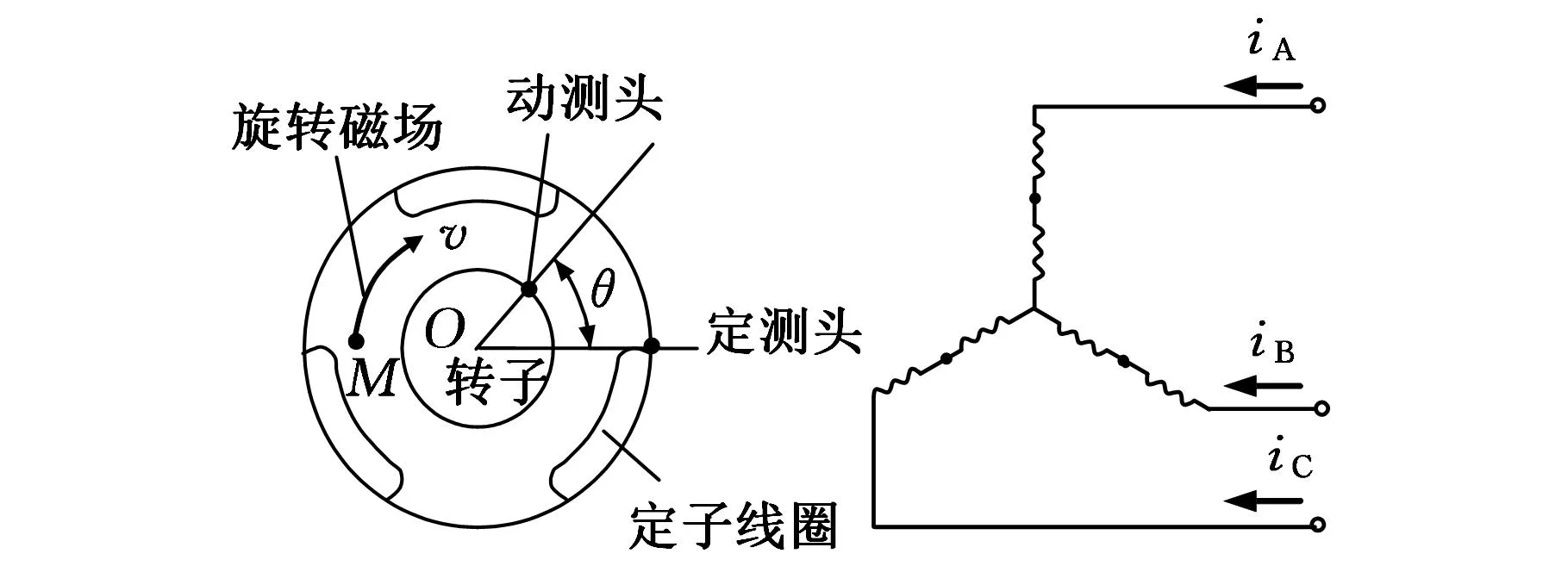
(a)工作原理

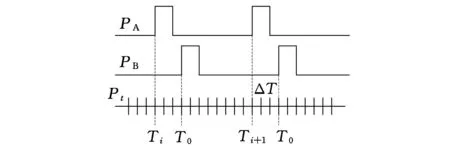
(b)信号处理图1　磁场式时栅位移传感器原理框图

根据传感器原理，如图1所示，在定子绕组中输入三相对称激励源，则会在传感器定子和转子的气隙中产生一个转速恒定的行波磁场M[10]。该行波磁场相当于时栅位移传感器原理中要构造的速度恒定的坐标系S′,传感器定子相当于坐标系S。此时，在传感器定子和传感器转子中各埋一根导线作为定测头和动测头，根据电磁感应定律，行波磁场将切割导线，两个测头将分别感应出感应信号，动测头跟随转子一起转动，因此动测头的感应信号已经具有了空间上的意义。由于定测头固定在传感器定子上，因此可以以定测头感应信号作为参考信号，再对两个感应信号比相[11]，就可以求得行波磁场扫描经过传感器动测头与定测头的时间差ΔT，由此计算转子转过的角度为

(1)

式中，T为标准周期；W为空间当量。

此时，在该模型中传感器极距的空间当量为

(2)

式中，p为时栅位移传感器的对极数。

2磁场式时栅位移传感器的动态仿真

充分考虑时栅位移传感器的实际应用情况，在原有静态仿真的基础上，对时栅位移传感器开展动态电磁仿真研究。在静态仿真模型的基础上引入一个运动单元——Band模块[12]。图2为磁场式时栅位移传感器静态模型和动态模型对比图。

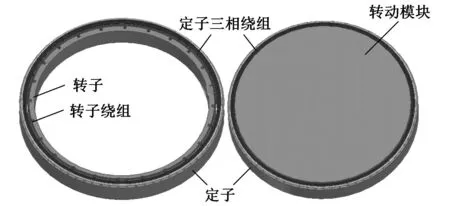
图2　时栅位移传感器静态、动态仿真模型

目前，磁场式时栅位移传感器比较成熟的产品是72对极的时栅位移传感器[13]，但是为了减少计算量、优化仿真过程，本研究以相同结构的12对极磁场式时栅位移传感器作为主要动态电磁仿真研究对象，研究时栅位移传感器的动态特性。仿真模型参数如表1所示，激励加载参数如表2 所示。

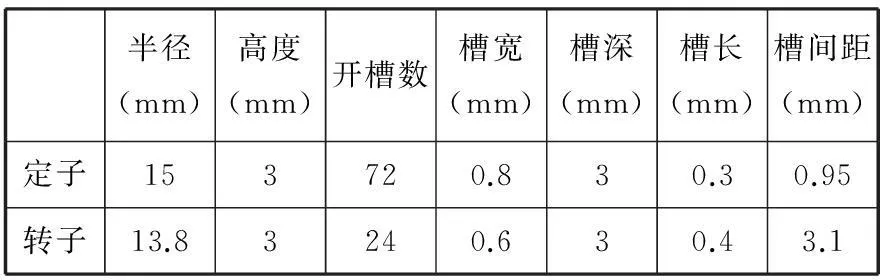
表1　时栅位移传感器仿真模型参数

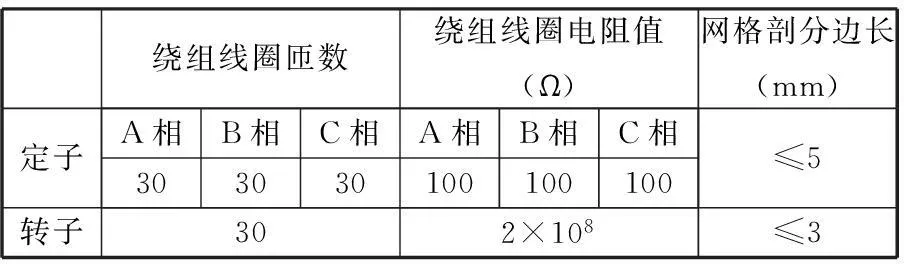
表2　时栅位移传感器模型激励参数

时栅位移传感器动态电磁仿真中传感器转速的设定将影响仿真精度与仿真效率，通过综合考虑，将仿真模型中时栅位移传感器的转子转速设为2 r/min、4 r/min、6 r/min、8 r/min、10 r/min，仿真时间设置为30 ms，步长为0.05 ms，尽量与传感器实际应用情况相吻合。表3所示为动态条件下磁场式时栅位移传感器各个转速下的感应电动势。在0～10 r/min的转速范围内，传感器感应信号始终为一行波，通过与实际测量的时栅位移传感器感应信号进行对比，发现其波形和幅值都是相吻合的。

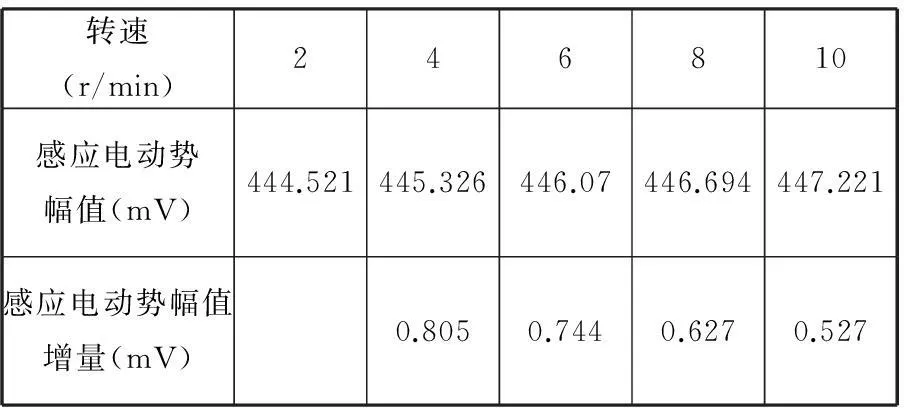
表3　不同转速下磁场式时栅位移传感器的最大幅值

由图3可知，随着时栅位移传感器转子转速的增加，传感器感应电动势的幅值呈递增的趋势。为了预测传感器在其他转速下的幅值信息，提取传感器各转速下感应电动势最大幅值，两两作差，可以得到不同转速下的感应电动势幅值的一阶差分曲线。

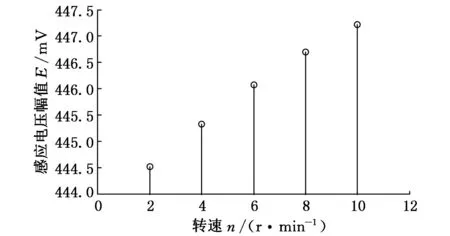
图3　感应电动势幅值曲线

图4为传感器感应电动势幅值一阶差分增长曲线，可以看出，随着时栅传感器转子转速的增加，其幅值的增长量越来越小，虽然在本研究的动态仿真模型中，设定的转速有限，但是根据其感应曲线的变化规律可以推测：随着转子转速的增加，其感应电动势的幅值增量先逐渐减小，然后逐渐增大，感应曲线呈正弦变化规律。

图4　感应电动势幅值差分增长曲线

3磁场式时栅位移传感器中的多普勒效应

无论是声波还是电磁波，当波源和观察者相对运动时，观察者接受到的频率与波源自身发出的频率存在差异，这就是多普勒效应[14-15]。磁场式时栅位移传感器中多普勒效应可以理解为传感器定子与转子间以恒定速度vS运动的旋转磁场和转子绕组中动测头随转子以速度vD运动之间的相对运动，因此其转子绕组接收到的频率可表示为

(3)

其中，f为激励信号的频率。当波源运动方向同其传播方向相同时取正号，当波源运动方向同其传播方向相反时取负号。转子转动方向同旋转磁场的运动方向相同时，其物理模型可表述为物理学中两个运动物体沿着同一个方向的追逐模型；当转子转动方向同旋转磁场的运动方向相反时，其物理模型可表述为两个运动物体的在同一条直线上相向运动的相遇模型。

3.1转速与感应信号幅值的关系

由第2节可知，随着转子转速的增大，感应电动势的幅值增大。为了定量地分析传感器的转速与传感器感应信号的幅值、频率之间的关系，在每种转速下设置仿真时间为30 ms,传感器的激励频率为400 Hz,周期为2.5 ms。因此，在30 ms的仿真时间内可以仿真出12个标准波形，点与点之间的采样时间为0.05ms。从每种转速下出现的12个波形信号中提取每个信号的感应电动势的最大值，绘制成曲线，得到图5所示的不同转速下传感器感应信号幅值。

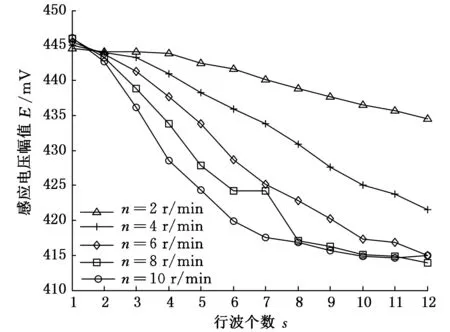
图5　时栅位移传感器各转速下的幅值曲线

从图5中可以看出，随着转速的增大，每个转速下第一个波形的感应电动势是逐渐增大的。在转速相同的条件下，随着时间变化，其感应电动势的幅值逐渐减小，在转速分别为2 r/min，4 r/min，6 r/min的条件下，幅值的变化率几乎固定。但是在8 r/min的转速下，第6个信号波形和第7个信号波形的幅值是相等的，第8个信号以后的波形中幅值变化较小。当转速为10 r/min时，与8 r/min时的情况类似，随着时间的变化，前6个信号幅值下降快，第7个信号和第11个信号之间幅值下降慢，到第12个信号时其幅值又开始上升。

由于在转速为10 r/min时，幅值随时间的变化先减小后增大，因此可以预测：当转速大于10 r/min的时候，感应电动势的幅值先快速减小，然后缓慢减小，之后又开始缓慢增大；当转速达到一定程度时，其感应信号就是一个正弦规律的包络信号。图6所示为传感器转速为50 r/min的感应信号，可以看出，虽然感应信号呈现出了正弦规律，但并非是标准正弦信号的形式，不利于后续信号处理。因此，可以判断时栅位移传感器的激励信号频率为400 Hz时，传感器运动速度的阈值为8 r/min。

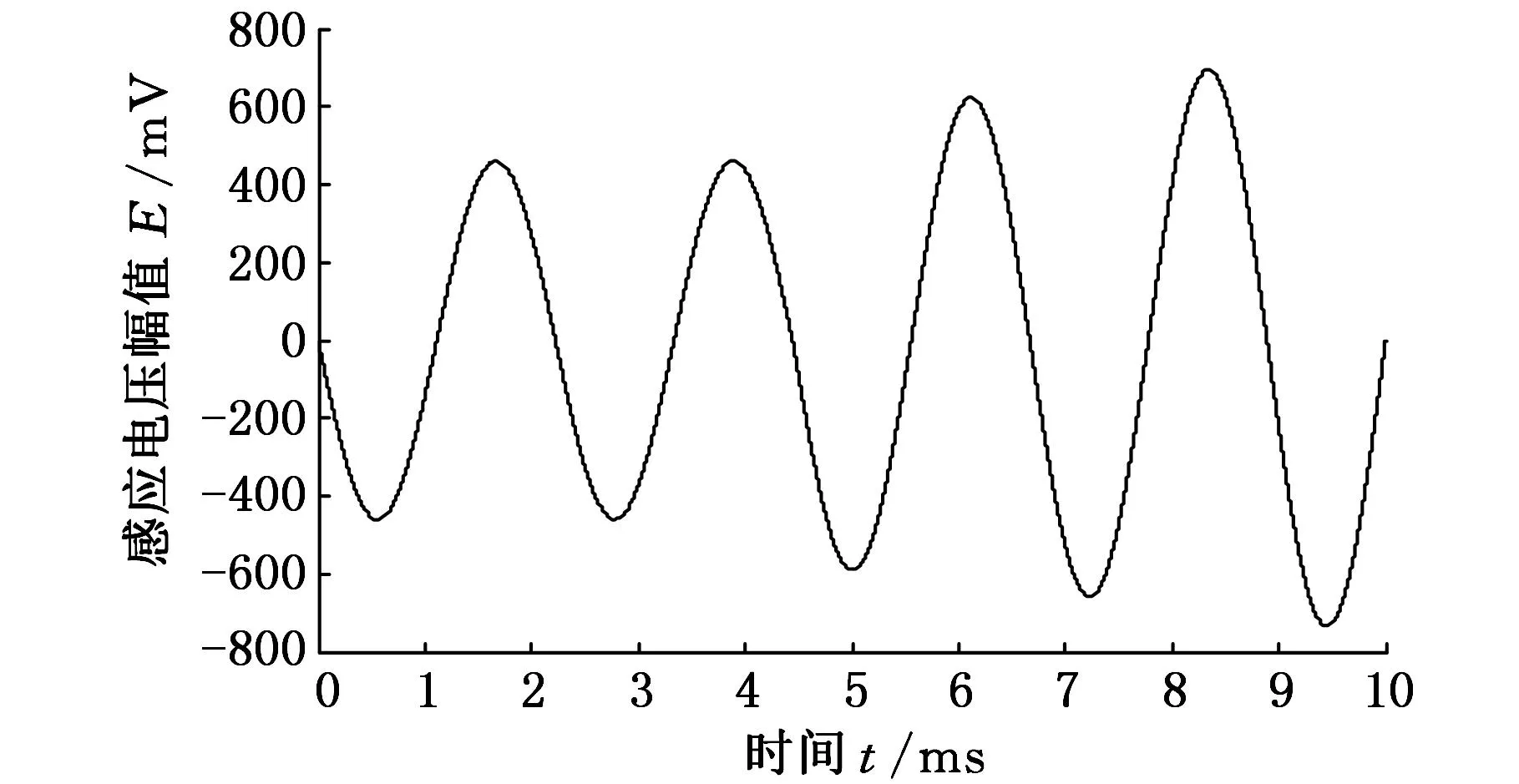
图6　50 r/min下时栅位移传感器感应信号

根据图5所示的感应电动势幅值信息还可以知道，磁场式时栅位移传感器的转子绕组感应信号的幅值随转速呈周期性变化，其形式可以表示为

A=gasinωt

(4)

式中，A为感应信号幅值；g为信号幅值的转子转速调制系数；a为相关参数；ω为感应信号角速度；t为时间。

3.2转速与感应信号频率的关系

为了定量分析时栅位移传感器感应信号与转速之间的关系，将各个转速下感应信号幅值最大值所对应的时间提取出来，见表4～表8。

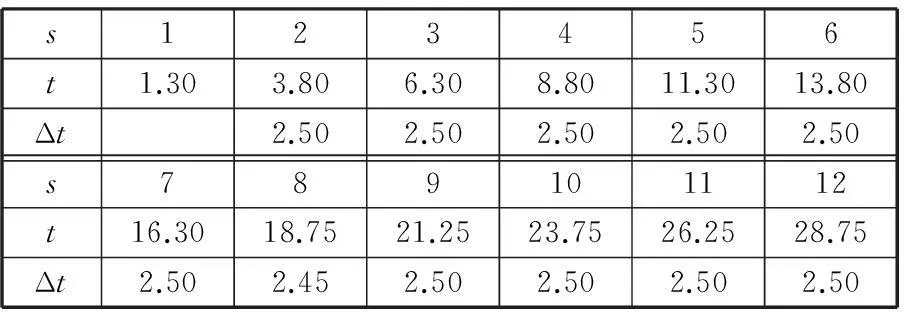
表4　转速为2 r/min感应信号最大值所对应的时间　ms

表5　转速为4 r/min感应信号最大值所对应的时间　ms

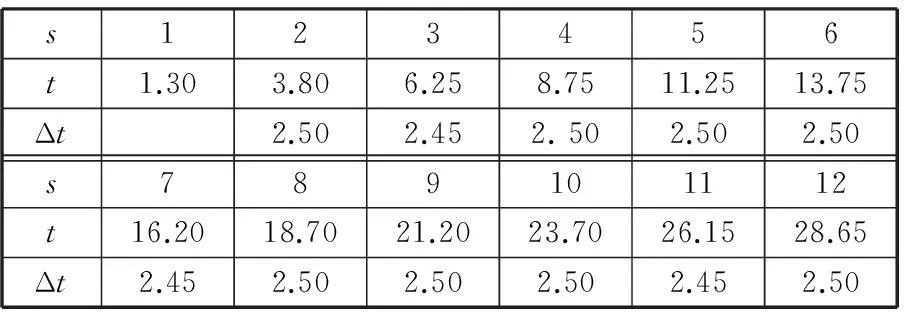
表6　转速为6 r/min感应信号最大值所对应的时间　ms

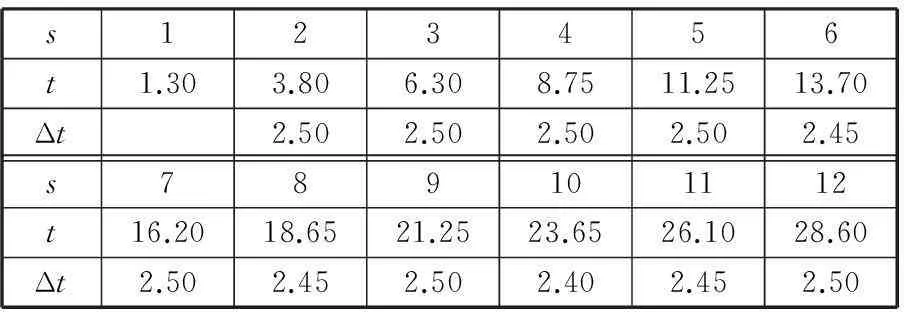
表7　转速为8 r/min感应信号最大值所对应的时间　ms

已知时栅位移传感器的仿真波形是呈周期性变化的，因此在两个信号幅值最大处取其所对应的时间即周期，在理论上应该是2.50 ms。当转速为2 r/min时，感应信号的周期发生1次变化，即在第8个信号处实际周期只有2.45 ms。同理，当转速为4 r/min时，感应信号的周期发生2次变化；当转速为6 r/min时，感应信号的周期发生3次变化；当转速为8 r/min时，感应信号的周期发生4次变化；当转速为10 r/min时，感应信号的周期发生5次变化。

综上所述，多普勒效应导致的感应信号频率变化规律为：感应信号频率变化的次数等于转速除以2。多普勒效应会直接影响时栅位移传感器的角测量精度。

4实验分析

为了进一步验证时栅位移传感器动态仿真结果，搭建了图7所示的实验平台。在实验系统中采用光栅(RD880)作为母仪，实验传感器为72对极的时栅角位移传感器，设计精度为±2″，时栅位移传感器和光栅通过弹性联轴器连接，在直驱电机的带动下进行同轴转动。因此时栅位移传感器的误差可表示为时栅传感器的测量值减去光栅的测量值。在开展时栅位移传感器动态误差实验之前验证时栅位移传感器的稳定性。将安装好的时栅位移传感器任意转动一个角度，待转台静止后进行一段时间的误差采样，考察时栅位移传感器的稳定性。图8a为实验时栅位移传感器转动到2° 52′ 9″时的稳定性测试曲线，图8b为时栅位移传感器转动到352° 8′ 41″时的稳定性测试曲线，从图8中可以看出，时栅位移传感器转动的两个角度的稳定性都达到0.5″，完全能够满足后续的实验要求。

图7　时栅位移传感器实验平台

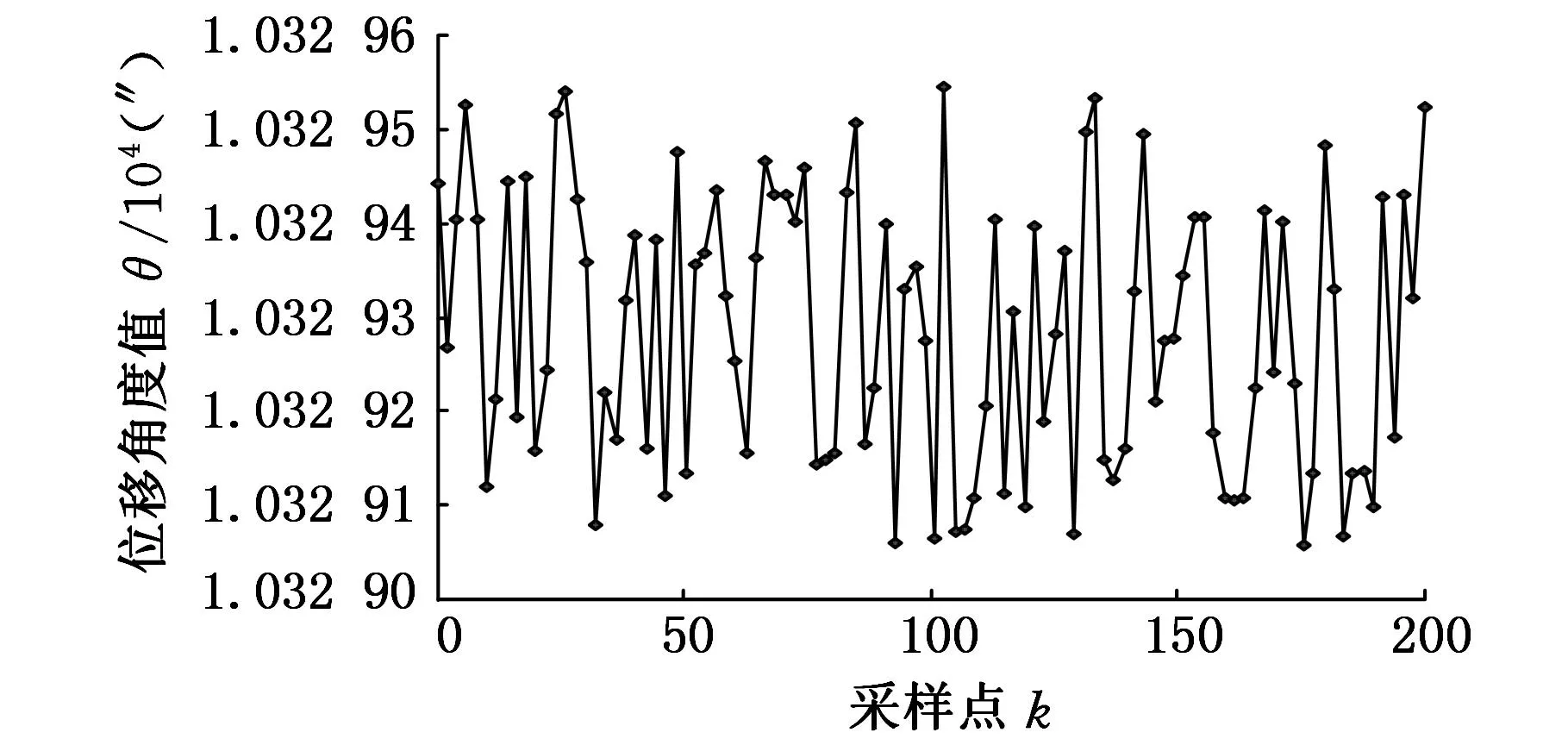
(a)传感器转至2° 52′ 9″

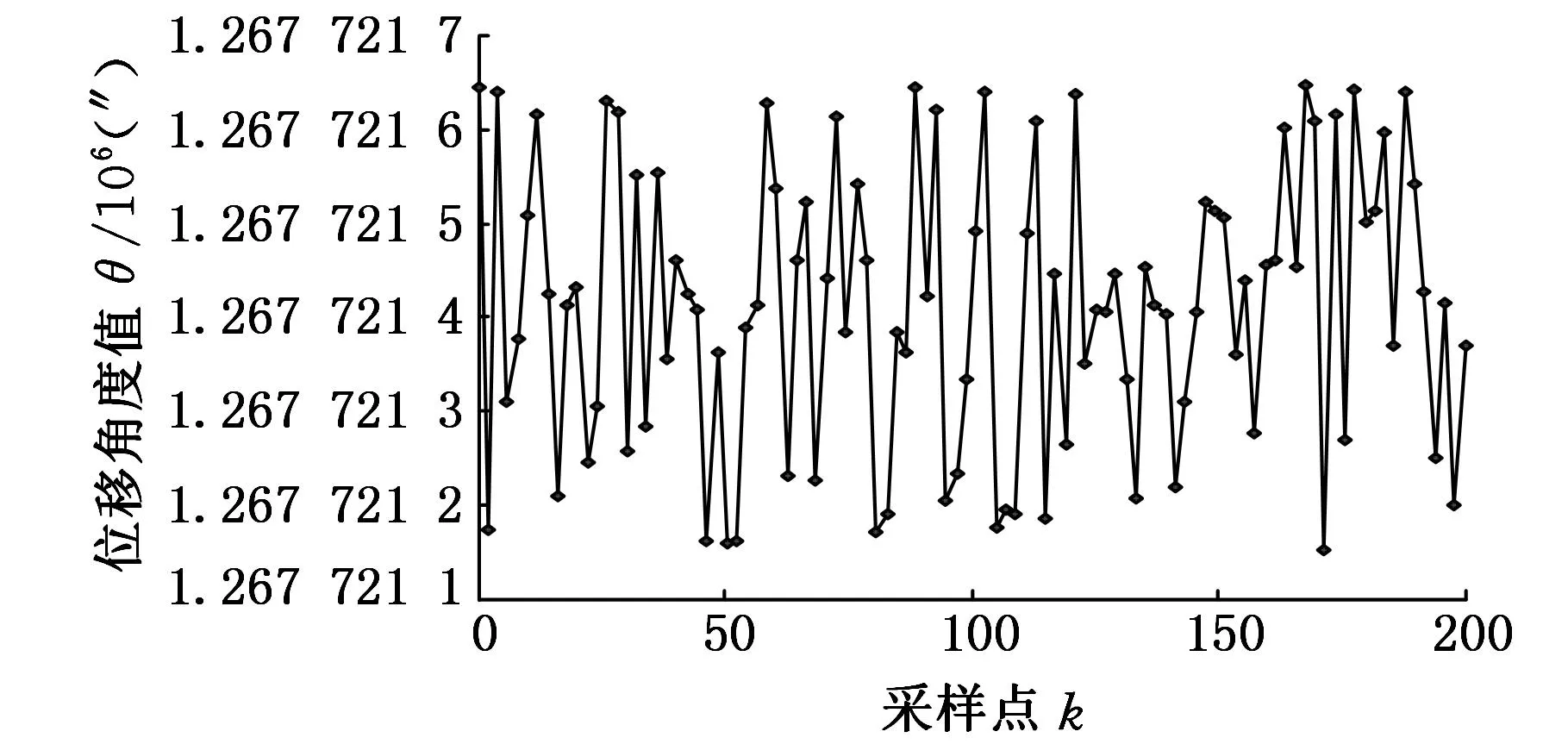
(b)传感器转至352° 8′ 41″图8　时栅位移传感器稳定性测试曲线

将转子转速分别设定为动态仿真时的转速，其误差如表9所示，转子转速在2 r/min时为±0.9″，8 r/min时为±1.4″,当转速达到9 r/min时其误差为±2.5″，转速达到10 r/min时误差为±8.2″，可以明显看出：当转速为0～8 r/min时传感器测量误差最大为±1.4″，基本满足运动规律与设计精度，转速提高将会对时栅传感器的测量精度产生一定的影响；当速度达到9 r/min时其误差为±2.5″，传感器精度出现了恶化的趋势，到10 r/min时测量误差已经达到±8.2″，远超传感器的设计精度。该实验结果也与时栅位移传感器动态仿真中的结果得到了一定的印证，这也为后续时栅位移传感器动态误差的修正与补偿研究提供了理论基础。

表9　时栅位移传感器动态误差

5结束语

时栅位移传感器动态仿真说明了传感器转子转速对感应信号幅值和频率的影响。实验结果表明，当传感器转速为0～8 r/min时传感器测量误差最大为±1.4″，满足运动规律与设计精度；当传感器转速超过8 r/min时，测量精度开始恶化，到10 r/min时，误差已经达到±8.2″，超过了设计要求，实验结果与动态仿真结果基本一致。该研究结果为后续时栅位移传感器运动测量中感应电动势的信号分析模型提供了依据。

参考文献：

[1]彭东林.时栅位移传感器与新型机床动态检测系统[M].北京:科学出版社,2010.

[2]方军, 陶红艳, 余成波. 盘式涡流永磁耦合器磁场分析[J]. 重庆理工大学学报(自然科学), 2016,30(3):40-46.

Fang Jun, Tao Hongyan, Yu Chengbo. Magnetic Field Analysis for Disc and Eddy Current Type of Permanent Magnet Couplers[J]. Journal of Chongqing University of Technology(Natural Science), 2016,30(3):40-46.

[3]武亮,陈锡候,王阳阳,等.磁导调制型时栅位移传感器测量方法研究[J].传感技术学报,2014,27(8):1043-1048.

Wu Liang, Chen Xihou, Wang Yangyang, et al. Research on the Measurement Method for Time Grating Sensor Based on Permeability Modulation[J].Chinese Journal of Sensors and Actuators, 2014,27(8):1043-1048.

[4]汤其富,彭东林,陈锡侯,等.锁定放大器在时栅位移传感器动态测量中的应用[J].仪表技术与传感器,2012(4):32-34.

Tang Qifu, Peng Donglin, Chen Xihou, et al. Application of Lock-in Amplifier in Dynamic Measurement with Time-grating Displacement Sensor[J]. Instrument Technique and Sensor, 2012(4):32-34.

[5]彭东林,汤其富,陈锡侯,等.变耦合系数型时栅位移传感器后期处理新方法[J].仪表技术与传感器,2012 (11):31-33.

Peng Donglin, Tang Qifu, Chen Xihou, et al. New Method of Postprocessing in Time-grating with Variable Coupling Coefficient[J]. Instrument Technique and Sensor, 2012(11):31-33.

[6]汤其富,彭东林,武亮,等.时栅角位移传感器中的多普勒效应影响及其抑制方法研究[J].仪器仪表学报,2014,35(3):620-626.

Tang Qifu, Peng Donglin, Wu Liang, et al. Study on the Influence of Doppler Effect and Its Suppressing Method in Time Grating Angular Displacement Sensor[J]. Chinese Journal of Scientific Instrument, 2014,35(3):620-626.

[7]刘小康,蒲红吉,郑方燕,等.纳米时栅位移传感器电场分布与误差特性研究[J].仪器仪表学报,2013,34(10):2257-2264.

Liu Xiaokang, Pu Hongji, Zheng Fangyan, et al. Research on Electric Field Distribution and Error Characteristics of the Nanometer Time Grating Displacement Sensor[J]. Chinese Journal of Scientific Instrument,2013,34(10):2257-2264.

[8]高忠华, 陈锡侯, 彭东林. 时栅角位移传感器在线自标定系统[J].光学精密工程,2015,23(1):93-101.

Gao Zhonghua, Chen Xihou, Peng Donglin. Online Self-calibration System for Time Grating Angular Displacement Sensor[J].Optics and Precision Engineering, 2015,23(1):93-101.

[9]郑方燕, 陈锡侯, 高忠华,等. 一种新型齿电式时栅位移传感器研究[J]. 中国机械工程, 2013, 24(3):396-398.

Zheng Fangyan, Chen Xihou, Gao Zhonghua, et al. Research on a Noval Electrical Gear Type Time Grating Displacement Sensor[J]. China Mechanical Engineering, 2013, 24(3):396-398.

[10]方军, 陶红艳, 余成波. 基于Ansoft的圆筒式永磁调速器传动特性影响因素分析[J]. 重庆理工大学学报:自然科学, 2015,29(12):64-70.

Fang Jun, Tao Hongyan, Yu Chengbo. Impact Factors Analysis of Transmission Characteristic for Cylindrical Permanent-magnetic Governor Base on Ansoft[J]. Journal of Chongqing University of Technology(Natural Science), 2015,29(12):64-70.

[11]Chen Z, Liu X, Peng D, et al. Dynamic Model of NC Rotary Table in Angle Measurements with Time Series[J].Transactions of the Institute of Measurement and Control, 2013,35(2):181-187.

[12]赵科义, 李治源, 程树康, 等. 单级感应线圈炮工作过程的动态仿真[J].高电压技术,2008,34(8):1667-1671.

Zhao Keyi, Li Zhiyuan, Cheng Shukang. Dynamic Simulation of Working Process of the Single-stage Induction Coil-gun[J]. High Voltage Engineering,2008,34(8):1667-1671.

[13]彭东林,张兴红,刘小康,等.场式时栅位移传感器研究[J].仪器仪表学报,2003,24(3):321-323.

Peng Donglin, Zhang Xinghong, Liu Xiaokang, et al. Study on the Time Grating Displacement Sensor of the Field Type[J]. Chinese Journal of Scientific Instrument,2003,24(3):321-323.

[14]朱志雄. 空间滤波测速研究进展[J]. 重庆理工大学学报:自然科学版, 2015, 29(2):91-97.

Zhu Zhixiong. New Development of Spatial Filtering Velocimetry[J]. Journal of Chongqing University of Technology(Natural Science), 2015, 29(2):91-97.

[15]刘立生, 张合勇,王挺峰,等. 激光外差探测对振动目标多普勒频谱成像[J]. 光学精密工程,2015,23(6):1508-1515.

Liu Lisheng, Zhang Heyong, Wang Tingfeng, et al. Doppler Spectrum Imaging of Vibrating Target Using Laser Heterodyne Detection[J]. Optics and Precision Engineering, 2015,23(6):1508-1515.

(编辑王旻玥)

收稿日期：2016-01-15

基金项目：国家自然科学基金资助项目(51205434，51275551);重庆市教委科学技术研究项目(KJ1400904);重庆市科技计划资助项目(cstc2014jcyjA70003)

中图分类号：TH712

DOI：10.3969/j.issn.1004-132X.2016.13.017

作者简介：杨继森，男，1977年生。重庆理工大学机械检测技术与装备教育部工程研究中心副教授。主要研究方向为精密测量与智能传感器。张静(通信作者)，女，1981年生。重庆理工大学电子信息与自动化学院讲师。江中伟，男，1988年生。重庆理工大学电子信息与自动化学院硕士研究生。李小雨，女，1989年生。重庆理工大学电子信息与自动化学院硕士研究生。

Study on Dynamic Performance of Time Grating Displacement Sensor

Yang JisenZhang JingJiang ZhongweiLi Xiaoyu

Engineering Research Center of Mechanical Testing Technology and Equipment,Ministry of Education,Chongqing University of Technology,Chongqing,400054

Abstract:In order to solve the dynamic measuring problem of time grating angular displacement sensor, through introducing motion unit module, a dynamic electromagnetic simulation model was established based on the static state electromagnetic simulation of time grating displacement sensor.The relationship among amplitude, frequency of the induced electromotive force and the speed of the rotor as well as magnetic field distribution was analyzed when time grating displacement sensor functions under its dynamic conditions. It is also predicted that the maximum speed is approximately 8 r/min theoretically when the time grating displacement sensor is running with 400 Hz excitation frequency. The experimental results show that the error of the time grating displacement sensor is as ±1.4″ under the speed of 0～8 r/min and when the rotary speed of the time grating displacement sensor exceeds 8 r/min, the error of the time grating displacement sensor begins to deteriorate. The error of the time grating displacement sensor is as ±8.2″ at the speed of 10 r/min.

Key words:time grating displacement sensor；dynamic simulation； induced electromotive force；rotor speed