基于末端杆件螺旋运动的凿岩机械臂孔序规划

王恒升　陈伟锋　王思远

中南大学高性能复杂制造国家重点实验室，长沙，410083



基于末端杆件螺旋运动的凿岩机械臂孔序规划

王恒升陈伟锋王思远

中南大学高性能复杂制造国家重点实验室，长沙，410083

摘要：根据隧道炮孔设计，进行孔序规划，是对凿岩机械臂进行自动控制所需要解决的一个问题。针对这一问题，以机械臂末端杆件的螺旋运动来定义其运动轨迹，用螺旋运动轨迹的曲线长度来定义机械臂将末端执行器从一个孔位运送到另一个孔位所付出的代价，以此代价为基础建立目标函数，用蚁群算法进行问题求解，得到机械臂运动的孔序规划。利用对偶四元数法推导了机械臂末端杆件螺旋运动参数的计算公式。仿真验证了轨迹求解算法，得到的轨迹平滑、连续；针对某隧道断面64组炮孔设计，利用蚁群算法进行左右两个机械臂的孔序规划仿真，得到了合理的规划结果。

关键词：孔序规划；螺旋运动；对偶四元数；蚁群算法；螺旋线性插值；凿岩机械臂

0引言

钻爆法是目前矿山、隧道、地下工程施工的主要工艺方法，凿岩台车是实现这一工艺方法的主要工程装备。在钻爆工艺过程的周期循环中涉及凿岩台车部分的主要任务，是通过操控凿岩台车串联机械臂的各个关节运动，把末端杆件上装配的凿岩钻机以一定的姿态运送到炮孔的设计位置，启动凿岩钻机，在设计的位置和方向上打出一定深度的炮孔。影响整个隧道开挖的工程质量、工程进度、工程造价的因素很多，涉及凿岩钻孔环节的主要有炮孔的精度、机械臂移动的速度等[1]。本文研究的目标是对钻孔的顺序进行规划，以缩短机械臂在各个孔位之间移动所花的时间，提高钻凿工序的工作效率；同时也可减小机械臂的磨损和运动过程的能量消耗；实际控制时还需考虑机械臂的运动干涉。

对于隧道断面布孔设计，孔序规划就是要寻求一种优化的孔序，使机械臂按照这一顺序逐个完成炮孔的钻凿。国外文献一般针对某炮孔设计，直接给出孔序规划的结果[2]。周友行等[3-4]研究了孔序规划的理论方法，把该问题看成旅行商问题(traveling salesman problem，TSP)的变种，从遍历孔的方案中找出最优方案，由于TSP是一个NP难题，故主要采用启发式的算法来寻优[5-6]。对于孔之间的移动代价，或者说路程的长短，有的简单地以炮孔的空间位置坐标直接计算两点的空间距离，有的则以机械臂所有关节的运动转角进行加权求和。上述方法均没有考虑机械臂的实际运行轨迹。

本文以机械臂末端杆件的运动轨迹为基础，定义炮孔之间的移动距离代价。末端杆件从一个炮孔对应的位姿状态移动到另一个炮孔对应的位姿状态，可以等价为空间坐标系之间的变换，根据Charles定理，这一变换可以等效为绕某个轴(称为“螺旋轴”)的旋转运动和沿该轴的平移运动(平移距离称为“螺距”)[7]，即将空间坐标系之间的变换等效为螺旋运动。在此基础上将螺旋运动轨迹的曲线长度定义为两个炮孔之间的距离，再进一步利用蚁群算法[8]，搜索遍历孔的最短路径[9]。详细介绍了螺旋运动的对偶四元数[10]表示、炮孔之间螺旋运动的关系推导及螺旋运动轨迹的长度计算，介绍了蚁群算法及孔序规划的应用，最后给出了仿真及仿真结果。

1末端杆件螺旋运动轨迹计算

图1所示为某煤矿岩石运煤通道的炮孔设计断面图，该断面设计有64个炮孔，由双臂凿岩台车实现炮孔钻凿。凿岩台车完成64个炮孔的钻凿后，进入装填炸药、爆破、通风、清渣等工序。

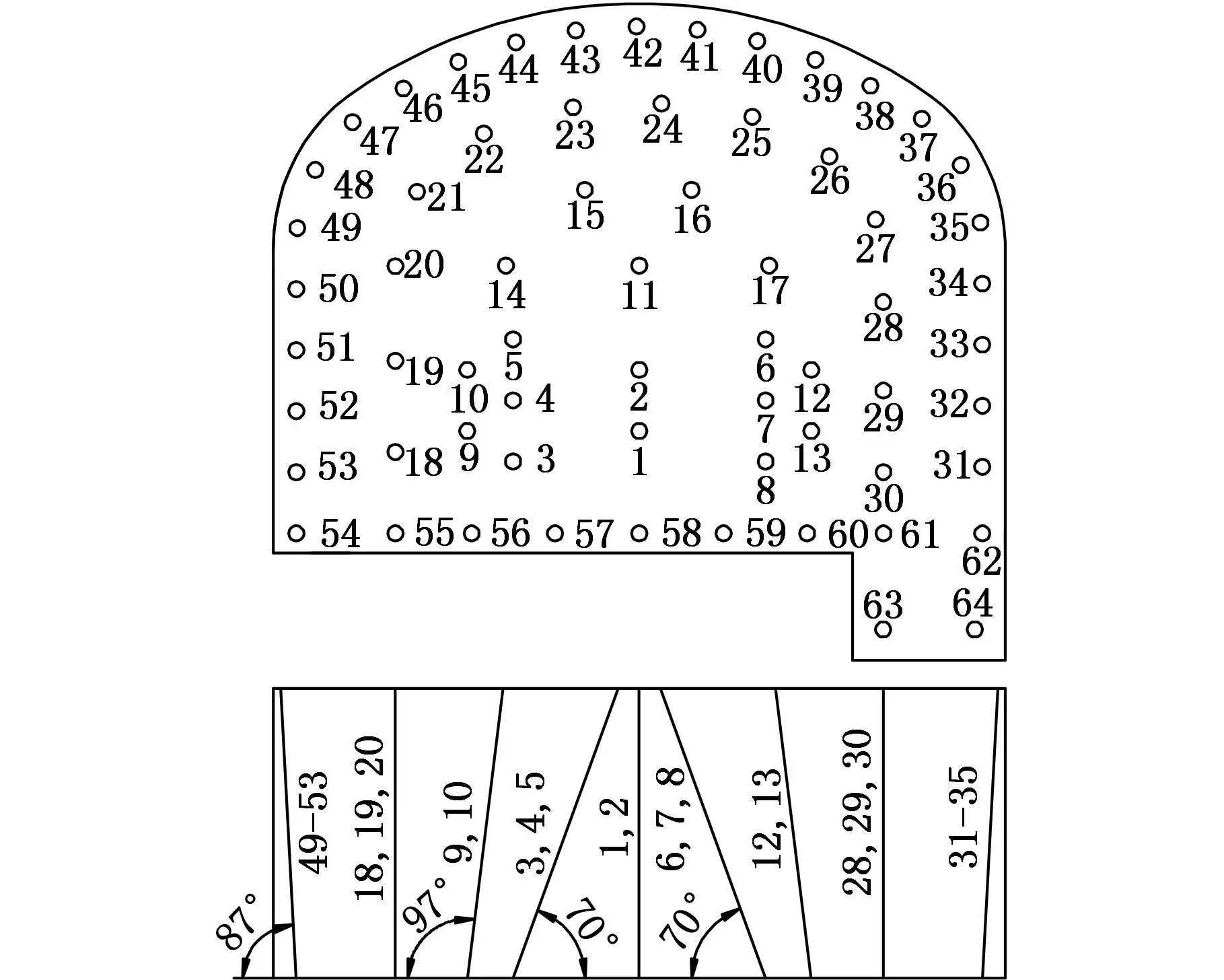
图1　炮孔设计断面图

1.1末端杆件姿态的四元数描述

某凿岩机器台车的六自由度机械臂如图2所示，末端杆件就是滑架6，末端执行器(即凿岩钻机)安装在滑架上。工作时通过机械臂各关节的运动把末端执行器运送到对应炮孔所设计的位姿状态，各炮孔对于末端杆件的位姿要求由炮孔的设计和机械臂的实际工作环境所确定。凿岩台车、机械臂及工作断面的示意图见图3，炮孔对末端杆件的姿态和位置要求见表1，表1中第2、第3列给出了部分与炮孔相应的末端杆件的原始数据，省略了其他炮孔对应的末端杆件的位姿数据。

1.关节6　2.车体　3.关节1　4.关节2　5.大臂　6.滑架　7.关节3　8.关节4　9.关节5图2　机械臂示意图

图3　台车、机械臂及工作断面的关系示意图

孔号炮孔位置坐标(mm)末端杆件姿态(α,β,γ)末端杆件位姿的对偶四元数5(-784.5,-1400,4900)(0,20°,-90°)(0.696,-0.123,0.123,-0.696)+ε(1743.880,-86.524,-1061.434,1571.977)6(784.5,-1400,4900)(0,-20°,90°)(0.696,-0.123,-0.123,0.696)+ε(-1743.880,86.524,-1061.434,1571.977)7(784.5,-1000,4900)(0,-20°,90°)(0.696,-0.123,-0.123,0.696)+ε(-1719.323,225.797,-922.161,1571.977)8(784.5,-600,4900)(0,-20°,90°)(0.696,-0.123,-0.123,0.696)+ε(-1694.765,365.070,-782.888,1621.093)9(-1150,-800,4900)(0,7°,-90°)(0.706,-0.043,0.043,-0.706)+ε(1721.626,-229.274,-793.904,1687.092)10(-1150,-1200,4900)(0,7°,-90°)(0.706,-0.043,0.043,-0.706)+ε(1730.260,-88.117,-935.062,1678.458)11(0,-1883.5,4900)(0,0,-90°)(0.707,0,0,-0.707)+ε(1732.412,665.918,-665.918,1732.412)

表1中的数据是相对固接在车体上的基础坐标系OvXvYvZv给出的，也就是固接在末端杆件上的坐标系O6X6Y6Z6相对于基础坐标系的空间位姿。其中，姿态角按欧拉角给出，旋转顺序为Y-X-Z，即先绕Y轴转β角，然后绕X轴转α角，最后绕Z轴绕γ角到达最终姿态。以上三个旋转变换的四元数[11]表达式为

(1)

由此，末端杆件姿态的四元数可由以上三个四元数的连续相乘得到：

qR=qYqXqZ=(q0,q1,q2,q3)

(2)

(3)

根据刚体的旋转变换，以上三个连续旋转等效于沿某单位矢量表示的旋转轴n=(nx,ny,nz)旋转θ角度的结果，即qR也可以写成以下等价三角函数形式：

(4)

由式(2)到其等价式(4)的参数变换如下：

(5)

1.2末端杆件螺旋运动的参数计算

图4中，空间坐标系O1X1Y1Z1到O2X2Y2Z2的坐标变换可以分为以下两步：

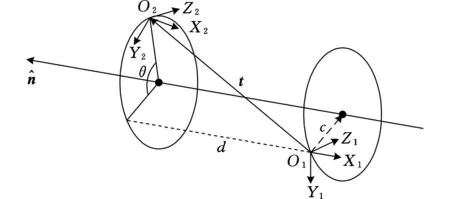
图4　坐标系O1X1Y1Z1到O2X2Y2Z2的坐标变换

(1)将坐标系O1X1Y1Z1沿向量t平移到与坐标系O2X2Y2Z2的原点重合的位置，用单位对偶四元数表示此平移变换，即

(6)

式中，qt为四元数(0,t)表示平移的量。

(2)再按式(4)将坐标轴绕通过原点的某单位向量n旋转θ角至与O2相应的坐标轴重合。这两步综合起来用对偶四元数表示为

(7)

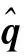
(8)

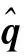
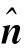
(9)

螺旋运动中的转轴是一空间直线，该直线用Plücker坐标表示为

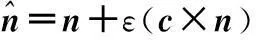
(10)

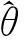
代入螺旋运动的参数，式(9)可表示为

(11)

对式(11)中的三角函数进行Taylor展开并整理可得以下对偶四元数表达式：

(12)

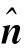
将式(7)的对偶部分展开并令其与式(12)的对偶部分相等，可得

(13)

对等式(13)进行化简，得

(14)

利用拉格朗日等式，有以下关系：

n×t×n=(n·n)t-(t·n)n=t-dn

(15)

将式(15)的右边与式(14)等号右边的第一部分相似，代入式(14)，有

(16)

将式(16)的右边两项共同提出叉乘因子n，对比两边可以得到

(17)

但实际上，由于c×n=(c+λn)×n对于任意实数λ都是成立的，所以满足式(16)的c有任意多个，从几何上说可以是螺旋轴上的任意一点。某些文献为了方便，直接取坐标原点的投影点，即取向量c与n相垂直，此时c由下式确定：

(18)

1.3末端杆件螺旋运动的轨迹插值

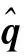
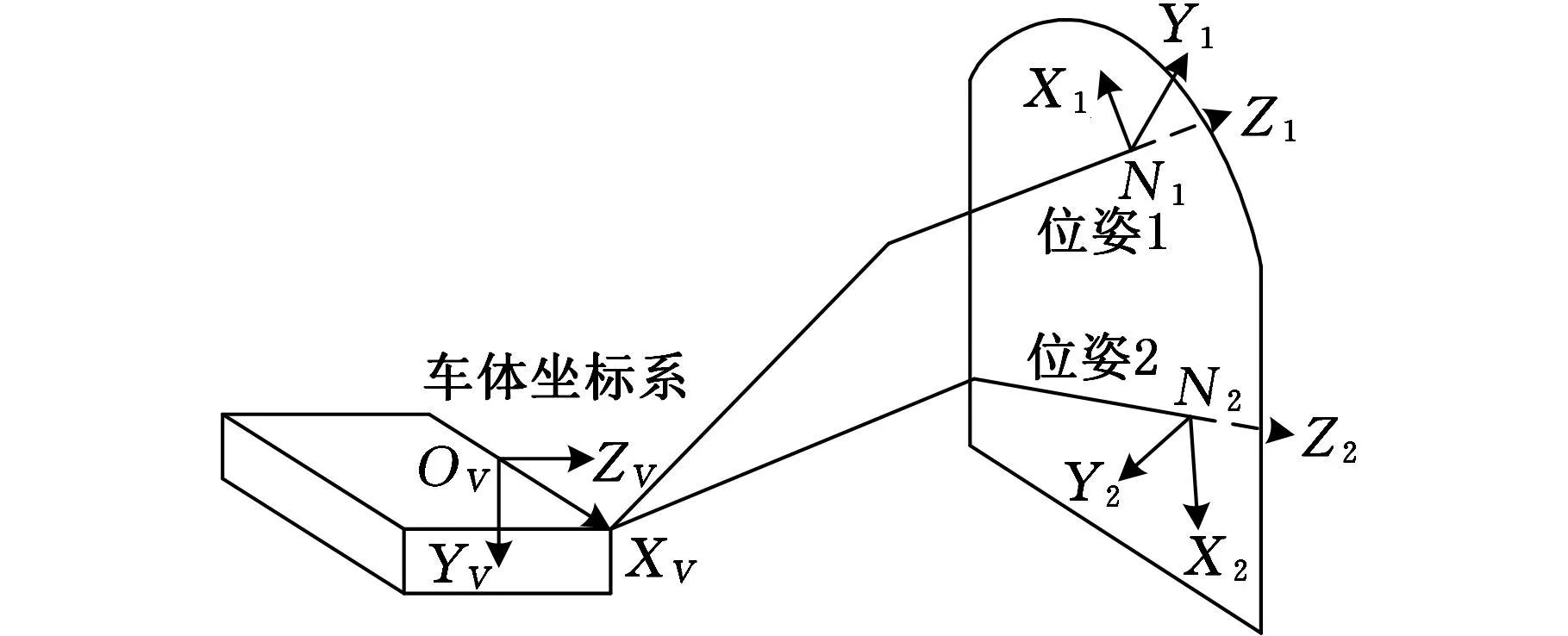
图5　从位姿1到位姿2进行螺旋轨迹插值

(19)

(20)

将式(20)表示为类似式(9)的单位对偶四元数的三角函数形式，有

(21)

(22)

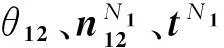
(23)

(24)

把式(23)代入式(19)可得到在车体坐标系中的插值公式：

(25)

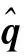
(26)

其中，qht=(0，th)可由式(8)计算得到，向量th是关于h的函数，也就是末端杆件坐标原点的Sclerp插值轨迹点在车体坐标系OvXvYvZv中的空间函数。

2孔序规划

2.1孔序规划问题描述

孔序规划问题，即钎杆末端从起始孔开始，遍历所有设计炮孔位的炮孔排序问题。施工时按排好的孔序进行钻凿，因此，序列中重复孔的排序是没有意义的。孔序规划问题是旅行商问题的变种，与旅行商问题相比，没有在遍历完后重新回到起始点的要求。所以孔序规划问题在数学求解上是一个NP难题。对于这类问题通常通过设计部分(而不是全部)搜索算法进行数值求解，也就是通过某种启发式的算法，不遍历全部解空间进行寻优，得到所谓的不一定是最优但实际上却是足够优的解[8,9,13-14]。本文采用蚁群算法进行孔序规划的问题求解。

2.2蚁群算法求解孔序规划问题

蚁群算法实际上是对自然界中的蚂蚁群体通过合作寻找出一条优化的觅食路线的现象的数学建模，通过数学的方法模拟这一自然现象，形成算法，解决寻优问题。

设有n个孔位，m只蚂蚁。在每一个时间步长内，每只蚂蚁经过一个孔位，因此，在n个步长的时间内，所有蚂蚁均遍历了n个孔位，完成一次迭代循环；为了防止在一次循环中蚂蚁重复已经经过的孔号，设置一个禁忌列表tabu，把经过的孔序号放入tabu中，当tabu中充满了n个孔号时，一次循环结束。与禁忌列表tabu互补的一个列表叫allowed列表，每一步蚂蚁可以从allowed列表中选择一个孔号。

2.2.1信息素

蚂蚁选择哪个孔号是按照概率计算进行随机选取的，蚂蚁会在自己经过的路径上留下信息素，或者说是在路径原有信息素的基础上增加一个信息素增量。本文采用蚁周模型[14](ant-cycle system)，即信息素增量的计算是每个蚂蚁走完一个周期(迭代循环一次)后进行的。例如，第k只蚂蚁在某周期完成后从第i个孔到第j个孔的路径上所留下的信息素增量为

(27)

其中，Q为信息量常数，Lk为第k只蚂蚁在本次循环中遍历的路径总长度。Lk值较小的蚂蚁，表现优秀，留下的信息素较大，在后面的路径概率选取上会有一定的优势。

经过一次迭代循环后全部m只蚂蚁在路径(i,j)上的信息素增量的总和Δτij以及信息素总量τij分别为

(28)

τij←ρτij+Δτij

(29)

式(29)为路径(i,j)上的信息素总量的更新算式，其中，系数ρ表示信息素持久性，取ρ<1以避免路径上信息素的无限增加，同时模拟自然界的一种自然遗忘的规律。

值得一提的是，一方面，这里的信息素增量和信息素总量是随迭代周期不断更新的，为了简化符号的写法，省去了公式中的迭代循环变量。另一方面，迭代开始时，蚂蚁是没有先验知识的，为了使状态转移机制可以实现，取初始值为一常数，即设τij(0)=C。

2.2.2路径选择概率

当蚂蚁k位于第i孔，选择下一步为第j孔的概率为

(30)

概率的大小除与路径上的信息素τij有关外，还与ηij有关。ηij表示选择路径(i,j)的期望程度，是一种启发因素，本文取ηij=1/d(i,j)，即路径长度越小，选择的可能性越高。α和β两个参数分别反映蚂蚁在选择过程中信息素和启发因素的相对重要程度。式(30)中，τij(t)中的t表示动态更新的含义，尽管在蚁周模型中信息素并不是每一步进行更新，而是一个循环更新一次；事实上如果采用蚁密(ant-density)或蚁量(ant-quantity)模型时，信息素的确是每走一步更新一次；此处为表达一致，仍然用τij(t)表示。

所有蚂蚁均遍历了n个孔位后完成一次迭代循环，选出最短路径的遍历方案；随着迭代循环的进行，期望最短路径能够收敛到一个最优值，即找到优化的炮孔排序方案。

3仿真

3.1空间位姿变换螺旋运动插值仿真

基于凿岩台车六自由度机械臂参数和隧道断面设计的几何参数，在MATLAB中进行了仿真计算。采用第2节给出的公式，只要给出凿岩钻机在任意两个炮孔要求的末端执行器位姿，即可得到连续平滑的螺旋运动轨迹。从13号孔(1150 mm,-800 mm,4900 mm，0,-7°,90°)到37号孔(1852 mm,-2871 mm,4900 mm,2°,1°,0)，对末端杆件坐标原点向量th运用Sclerp插值法进行了10 000次插值。图6所示为末端杆件坐标系运动轨迹，描述了位姿的渐变过程。图7所示为从13号孔到37号孔末端杆件的移动轨迹。杆件长度为4 m,图7中已标出近车体段和近断面端(图7)。

图6　从13号孔到37号孔坐标系的变化过程

图7　从13号孔到37号孔杆件的移动过程

插值过程得到的螺旋运动角度θ1h和平移位移d1h都是关于h的线性函数，进一步验证了第2 节的结论。为节省篇幅，此处省略了插值曲线。

从13号孔到37号孔的末端杆件螺旋曲线轨迹长度的计算结果为2430.6 mm(即图6的曲线长度)。

为了更形象地表现出末端杆件坐标系的运动轨迹，给出右臂的一个连续工作孔序，见表2。按照第2节的计算公式，把坐标系原点的空间轨迹投影到隧道断面上，得到图8的结果，此孔序列始于59号孔，连续移动经过10个孔后回到59号孔的位置。

3.2孔序规划的蚁群算法仿真

利用蚁群算法，取信息素迭代初值C=10-2，启发因素的期望程度因素ηij=500/d(i,j)，信息素持久系数ρ=0.7，信息量常数Q=15 000，蚂蚁的随机选择中信息素和启发因素的重要因子α=β=1，蚂蚁数量m=32，迭代次数取1000。左右臂按工作空间的区域分别平均分配32个炮孔(图9所示的两组炮孔)，给定左臂的起始孔为54，给定右臂的起始孔为58，在MATLAB中进行仿真计算。

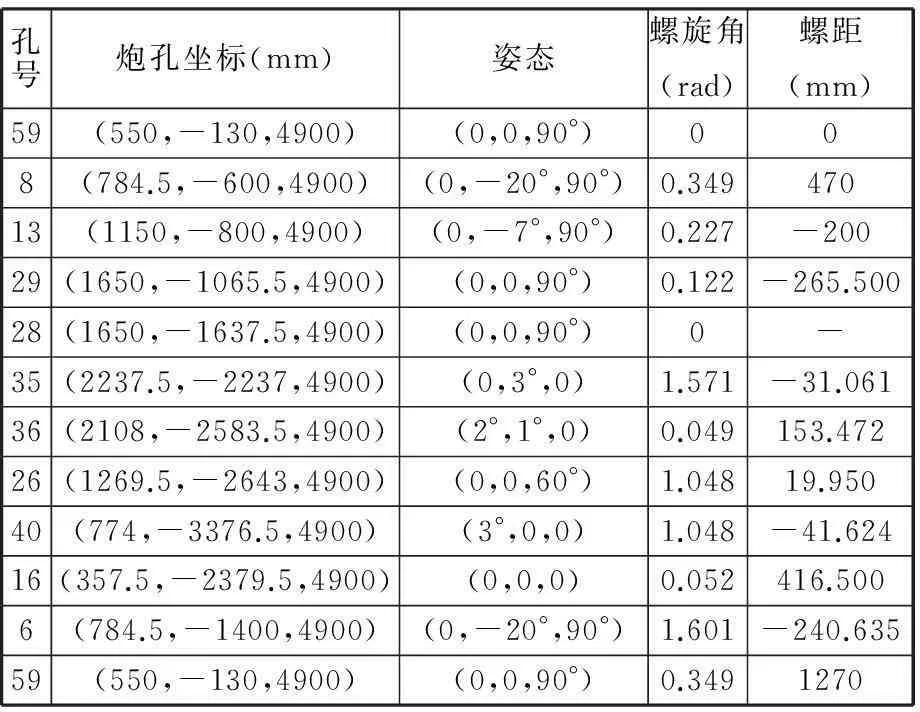
表2　右臂的试验工作孔序

图8　右臂末端杆件坐标系的连续11次螺旋运动轨迹在断面上的投影

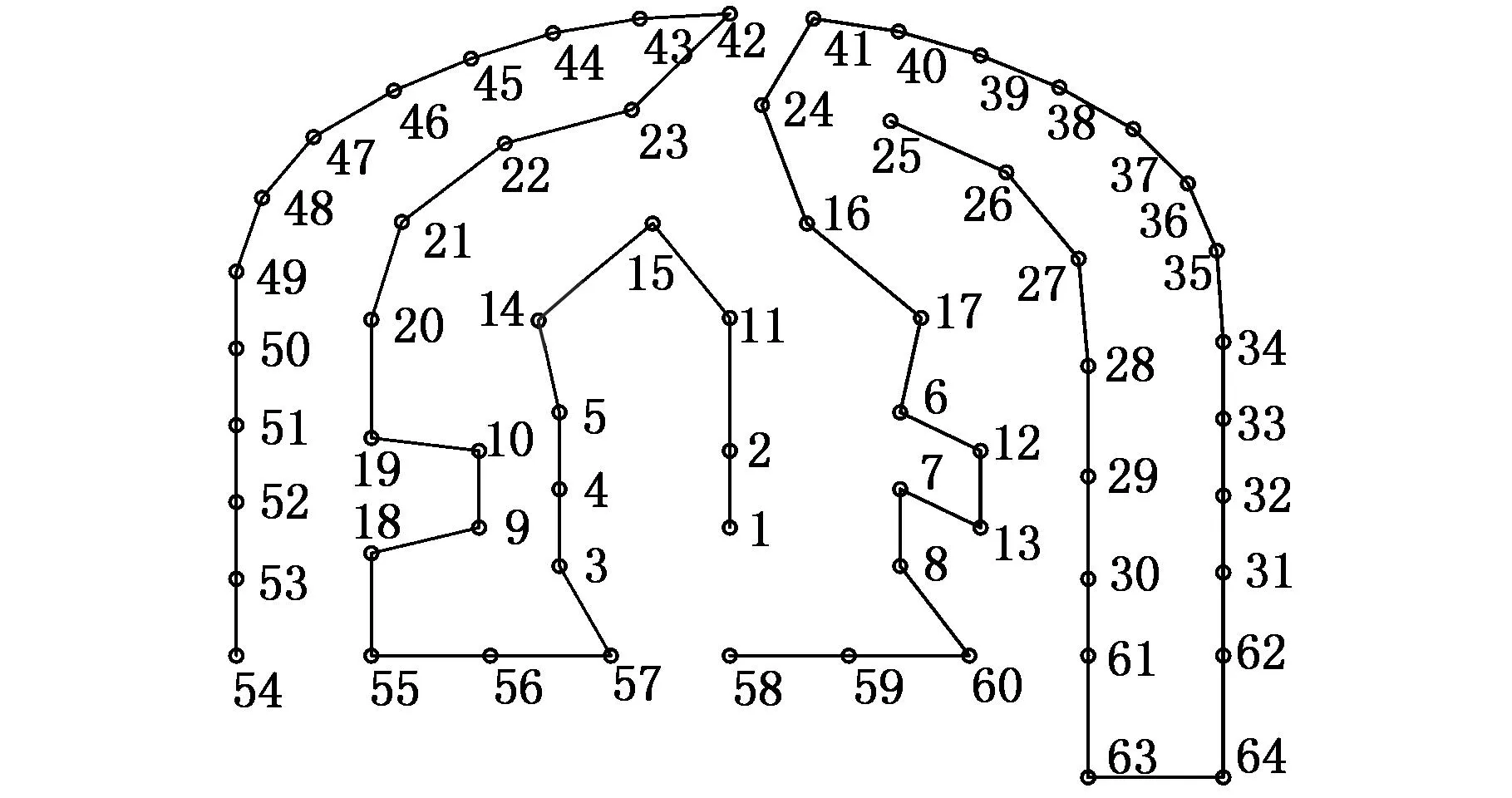
图9　孔序规划的结果

图9所示为两臂孔序规划的结果，图中连线不代表杆件末端空间真实轨迹，只用作排序显示。左臂末端杆件运动轨迹的最小距离为15 231 mm，右臂的最小距离为15 244 mm，两臂轨迹总距离差为13 mm,小于任意两个孔之间的最短距离。两臂的孔序路径的直观效果也很理想。图10所示为左右两臂孔序规划蚁群算法的迭代过程，迭代200次以后蚁群的路径已经非常集中了，平均路径与最短路径也非常接近；可以看出最小距离和平均距离的收敛趋势和过程非常好。

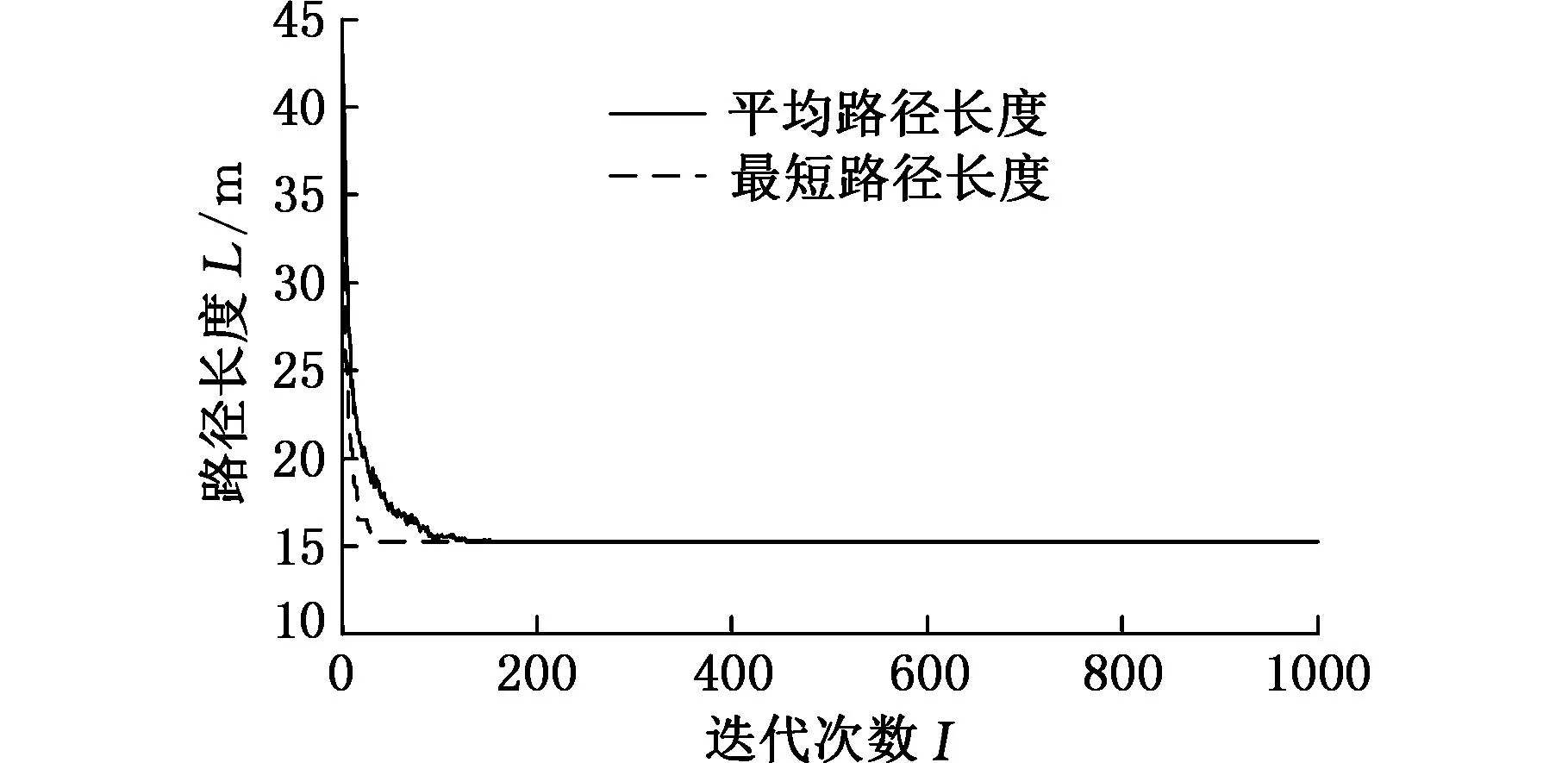
(a)左臂路径迭代

(b)右臂路径迭代图10　孔序规划蚁群算法的最优路径和平均路径仿真过程

4结语

本文针对隧道凿岩机器人(凿岩台车)操作臂的孔序规划展开研究。就机械臂的轨迹规划问题，提出末端执行器螺旋运动的轨迹规划，按照这种轨迹，末端执行器的运动过程平稳，路径最短，有利于提高机械臂的工作效率、减少运动磨损和能量消耗。基于对偶四元数法，详细推导了末端执行器螺旋运动的轨迹参数计算公式。运用四元数表达空间杆件的姿态及坐标变换，表达形式紧凑、直观，运算过程简洁明了。以末端执行器螺旋运动的轨迹长度作为从一个孔到另一个孔移动的代价，建立了孔序规划的目标函数，寻求最短的炮孔遍历路径。针对某煤矿运煤岩石隧道断面设计的64组炮孔参数，运用蚁群算法进行了优化，迭代算法的收敛过程非常理想，得到了实用的孔序规划的结果。本文从孔序规划的角度给出末端执行器理想的螺旋运动轨迹，未涉及关节的运动及机械臂的运动干涉问题，在实际机械臂的控制中需要考虑这些问题。

参考文献：

[1]Kukkonen J.The Art of Drill Plan Design[C]// Proceedings of World Tunnel Congress 2008-Underground Facilities for Better Environment and Safety.Agra,2008:1017-1023.

[2]Andersson K.Simulation of a Tunnel Drilling Sequence to Determine Loads on a Rock Drilling Equipment[C]//ADAMS User Conference.Rome, 2000:1-11.

[3]周友行, 何清华,谢习华.基于遗传算法的凿岩机器人孔序规划[J].机器人,2002,24(1): 62-65.

Zhou Youxing, He Qinghua, Xie Xihua. Application of Genetic Alogorithm to Bore Planning of the Tunnel Drilling Robot[J].Robot,2002,24(1): 62-65.

[4]周友行, 何清华.双臂凿岩机器人离散任务规划[J]. 中国机械工程, 2006, 17(13): 1334-1337.

Zhou Youxing, He Qinghua. Discrete Task Planning of Drilling Robot with Two Booms[J].China Mechanical Engnieering,2006,17(13):1334-1337.

[5]Woeginger G J.Exact Algorithms for NP-hard Problems:a Survey[M].Berlin:Springer Berlin Heidelberg, 2003.

[6]Applegate D L.The Traveling Salesman Problem: a Computational Study[M].Princeton:Princeton University Press, 2006.

[7]武元新.对偶四元数导航算法与非线性高斯滤波研究[D].长沙:国防科学技术大学, 2005.

[8]Brand M, Masuda M, Wehner N, et al. Ant Colony Optimization Algorithm for Robot Path Planning[C]//International Conference on Computer Design and Applications.Qinhuangdao,2010:436-440.

[9]Dorigo M, Gambardella L M. Ant Colony System: a Cooperative Learning Approach to the Traveling Salesman Problem[J].IEEE Transactions on Evolutionary Computation,1997,1(1): 53-66.

[10]Sariyildiz E, Temeltas H. A New Formulation Method for Solving Kinematic Problems of Multiarm Robot Systems Using Quaternion Algebra in the Screw Theory Framework[J].Turkish Journal of Electrical Engineering & Computer Sciences, 2012,20(4):607-628.

[11]Shoemake K. Animating Rotation with Quaternion Curves[J].ACM SIGGRAPH Computer Graphics. ACM, 1985, 19(3): 245-254.

[12]Kavan L, Collins S, Žára J, et al.Geometric Skinning with Approximate Dual Quaternion Blending[J]. ACM Transactions on Graphics,2010,27(4): 995-999.

[13]Bianchi L, Dorigo M, Gambardella L M, et al. A Survey on Metaheuristics for Stochastic Combinatorial Optimization[J]. Natural Computing an International Journal, 2009, 8(2): 239-287.

[14]李士勇.蚁群算法及其应用[M].哈尔滨：哈尔滨工业大学出版社,2004.

(编辑陈勇)

收稿日期：2015-01-27

基金项目：国家重点基础研究发展计划(973计划)资助项目(2013CB035504)

中图分类号：TP24

DOI：10.3969/j.issn.1004-132X.2016.13.010

作者简介：王恒升，男，1963年生。中南大学机电工程学院教授、博士研究生导师。主要研究方向为机电一体化及智能机器人。陈伟锋，男，1989年生。中南大学机电工程学院硕士研究生。王思远，男，1992年生。中南大学机电工程学院硕士研究生。

Drilling Sequence Planning Based on Screw Motion of End Lever of a Tunneling Rig Manipulator

Wang HengshengChen WeifengWang Siyuan

State Key Laboratory for High Performance Complex Manufacturing,Central South University,Changsha,410083

Abstract:One of the problems in the development of computerized tunneling rig is to make a drilling sequence according to a drill pattern design, which is the focus of this work. ACO algorithm was used to get a satisfactory sequence for a drill pattern,where the objective function was based on the trajectory length of screw motion of the end effector transported from one hole position to the next by the manipulator. The formulas were derived for the calculation of the screw motion parameters of the end effector with dual quaternion expressions. Simulations verify the algorithm of screw motion of the interpolation of the trajectory and the trajectory calculated is smooth and continuous. It turns out to be a practical drilling sequence resulting from the ACO algorithm for a prescribed drill pattern with two manipulators (right and left) of a 64-hole tunneling design.

Key words:drilling sequence; screw motion; dual quaternion; ant colony optimization(ACO) algorithm; screw linear interpolation; tunneling rig manipulator