基于滑模控制算法的风电系统变速变桨距控制研究

朱银珠, 米　阳, 杨慧霞

(上海电力学院 电气工程学院, 上海　200090)



基于滑模控制算法的风电系统变速变桨距控制研究

朱银珠, 米阳, 杨慧霞

(上海电力学院 电气工程学院, 上海200090)

为改善系统恒功率输出运行区域内的动态性能,基于趋近律方法设计了滑模多变量控制器,将发电机转矩加入风电系统与桨距角同时调节,不但能保证发电机功率和转速稳定在额定值附近,而且可以降低传动系统扭转力矩波动和桨距角活动频率,在提高风电电能质量的同时可以减少系统机械部分的压力.最后利用Matlab对高风速下系统多变量与单变量控制策略进行了仿真对比,突出多变量控制策略的优越性;并将提出的滑模控制与PI控制进行仿真对比分析,以验证本文控制算法的有效性.

风力发电系统; 变速变桨距; 滑模控制

由于风能清洁无污染,取之不尽用之不竭,已成为近年来最具竞争力的可再生能源.但由于风能具有能量密度低、随机性和不稳定性等特点,且风力发电机组是复杂多变量非线性不确定系统,因此风电机组的控制技术是系统安全高效运行的关键.随着风力发电机组的大型化以及风能渗透进电能市场的必然性,提高风能转换率和降低风力发电成本至关重要,高风速下风电机组的控制已成为风力发电的关键技术之一.

高风速下典型的功率调节控制方案是将桨距角作为风电系统的唯一控制输入变量,发电机转矩的调节大多用于低风速条件下追寻最大风能利用率,而在高风速时保持在其额定值[1].桨距角的功率调节能力受限于其变化率,有滞后延迟反应,当遇到急速变化的风速时不能快速响应;发电机的转矩控制较快,但当其应用于受限制的输出功率和转速时,容易出现稳定性问题.单变量控制器无法很好地满足调节输出功率和转子速度等多个目标的需求[2-4].当这两个控制一起工作时,在变速模式下,控制发电机的转矩能够减少桨距角执行机构的局限性产生的影响,改善瞬态响应和稳定性问题.这种多变量控制系统同时调节电磁发电机转矩和风轮机桨距角,能够有效降低传动系统扭动转矩和桨距执行机构的疲劳度及部件之间的摩擦,延长其使用寿命和降低故障的发生,同时提高风能系统的电能质量.然而,多输入多输出系统会导致控制设计更加复杂,而且由于风力发电系统中包含大量的非线性和不确定环节,使得传统的PI控制调节效果变差,很难实现预期的控制目标.

目前已有部分文献利用智能控制方法研究高风速下变速变桨距(Variable Speed Variable Pitch,VSVP)风力发电系统的控制问题[2-8].文献[4]为滑模多目标变桨距控制,能够有效抑制载荷并保持机组转速恒定,但是桨距角变化率较大.文献[8]为多变量控制模型预测控制技术,较好地平滑了输出功率,但是以牺牲较大的转速波动为前提.文献[9]利用滑模控制(Sliding Mode Control,SMC)技术对高风速下的风电系统进行单变量桨距角控制,该方案起到了平滑转速和减少桨距角活动频率的效果,但控制设计相对复杂且与PI相比并没有特别突出的优势.文献[10]对变速变桨距风电系统进行了积分滑模控制,但高于额定风速时仍只采用单变量桨距角控制,较其他控制方法没有特别突出的优势.这些研究工作虽在一定程度上解决了系统不确定性的影响,但也存在控制复杂、鲁棒性差等问题.

滑模控制策略针对非线性和不确定系统具有较强的鲁棒性和抗干扰性等优点,可用来处理风电系统中风能扰动的变化和发电机变化率受限等问题.但由于滑模控制器的设计是基于模型的,所以建立适当的模型对于控制器的设计非常关键.对于风电系统,特别是变速变桨距多变量风电系统,其控制器的设计更加复杂.建立包含不确定扰动的线性化模型,既可以准确逼近原系统,又可以方便控制器的设计和应用.本文基于滑模控制理论,提出风力发电系统的多变量控制策略:建立风力发电系统的机理模型,并在稳定的工作点对模型进行线性化;设计滑模变速变桨距多变量控制器;对变速变桨距与变桨距控制策略进行仿真对比分析,说明变速变桨距风电系统的优越性;将设计的滑模控制器与典型PI控制器进行仿真对比分析,表明该控制策略在调节风机转速时可有效地平滑输出功率,并可降低传动系统扭转力矩波动及桨距角活动频率,对风力的变化扰动具有良好的鲁棒性.

1　风力发电系统的建模

1.1风力发电机系统模型

变速变桨距风力发电系统的结构原理如图1所示[3].风力涡轮机模型由风力机模型、传动系统模型、发电机模型、变桨距执行机构模型4个部分组成.

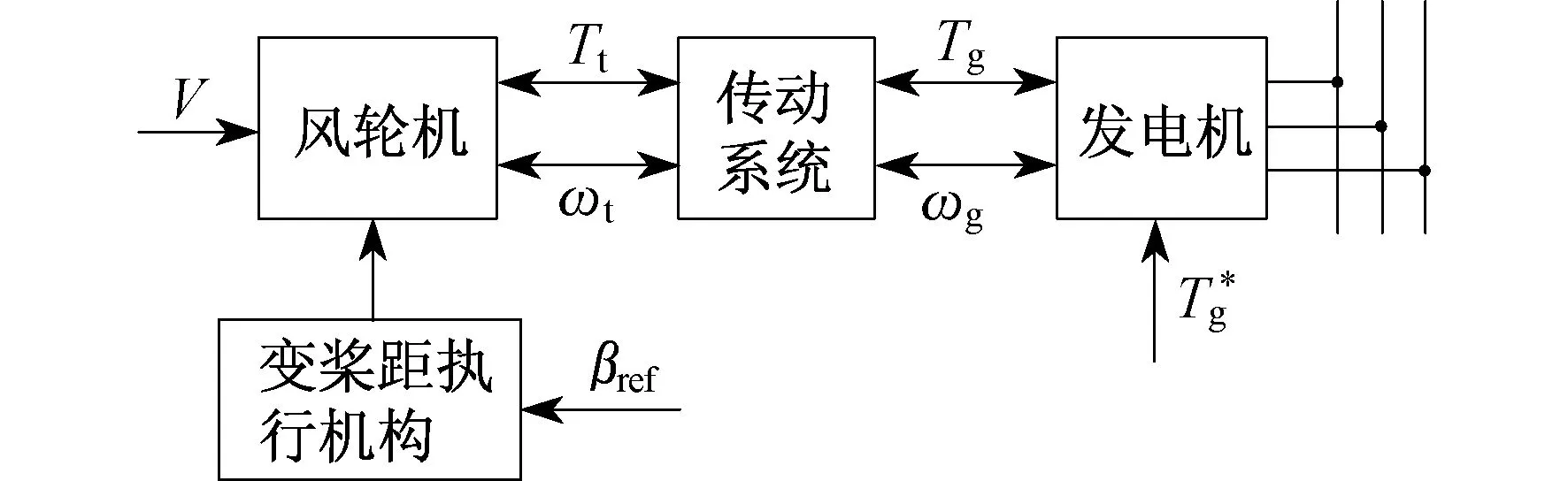
图1　变速变桨距风力发电系统的结构原理

风力发电系统描述风轮将风能转换为动能并通过风力涡轮机转子向机械功率的转换.

(1)

式中:Pt——风力机输出功率;

Tt——风轮转矩;

ρ——空气密度,取1.225 kg/m3;

R——风轮半径;

V——风速;

ωt——风轮的角速度;

β——桨距角;

λ——叶尖速比,λ=ωtR/V;

CP(λ,β)——风能利用系数,是关于β和λ的非线性函数[6].

传动系统连接风轮机和发电机,是将风轮机叶片的气动扭矩传输到发电机轴的机械部件.传动系统设备质量的高低会影响风力发电机的输出功率.模型的复杂性取决于特定系统,本文用两阶柔韧传动系统表示[6].

(2)

传动系统扭动转矩表达式为:

(3)

式中:Jt,Jg——风轮机和发电机的转动惯量;

i——传动比;

ωg——发电机的角速度;

Tg——发电机的转矩;

ks,Bs——传动轴的弹性系数和阻尼系数;

θtw——轴扭转角.

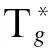
(4)

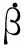
(5)

风速模型是Kaimal频谱[11].其基本数据如下:额定风速为12.5 m/s,切出风速为27.5 m/s.仿真结果如图2所示.

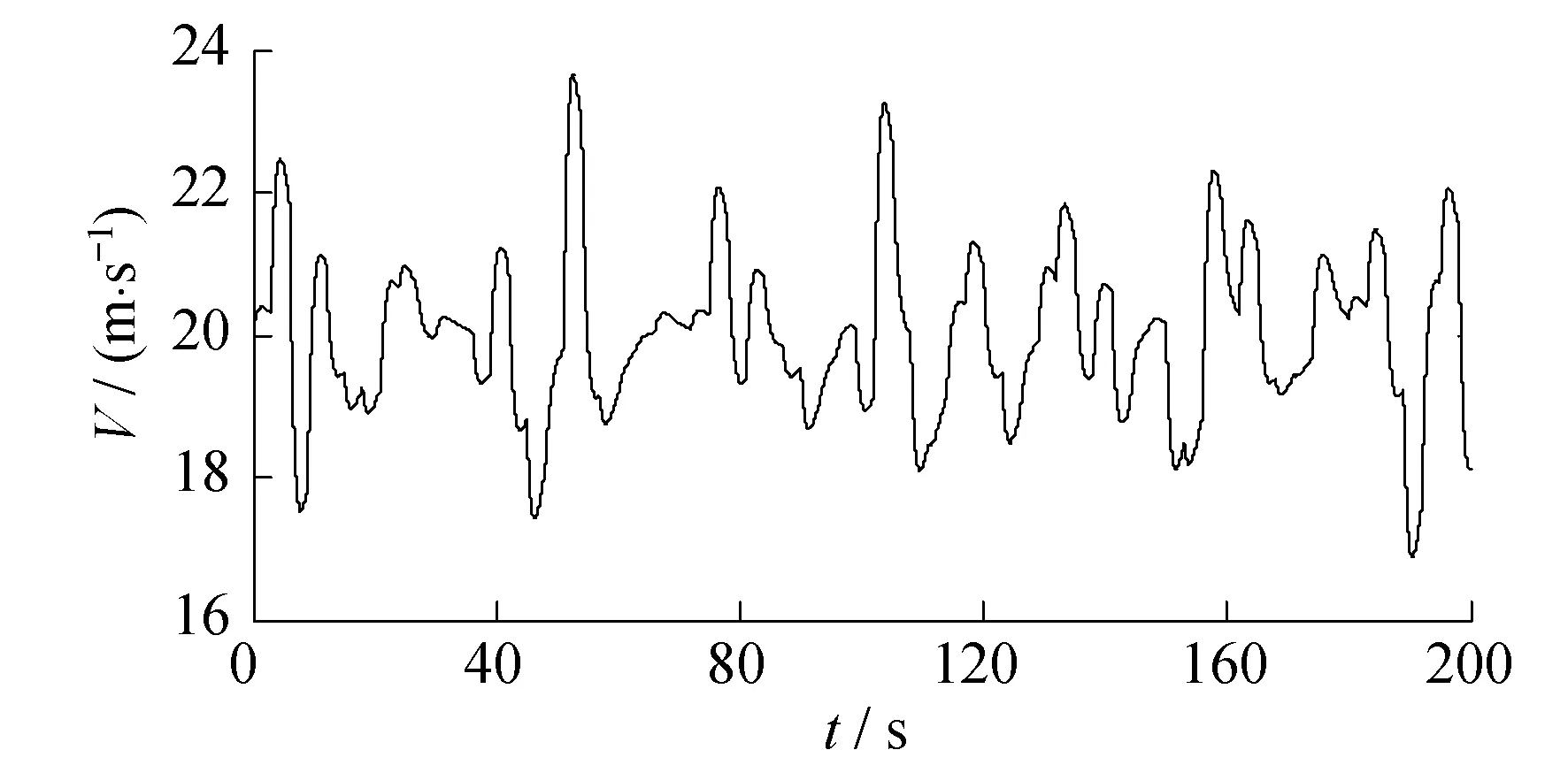
图2　风速仿真结果

1.2风力发电系统模型的线性化

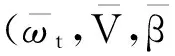
(6)

(7)

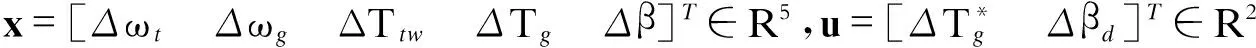
因此,线性化状态空间模型为:

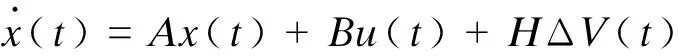
(8)

其中:

2　滑模控制器的设计

对非线性不确定系统而言,滑模控制是一种非常有效的鲁棒控制方法,其非线性表现为控制的不连续性.其基本原理为:通过设计切换函数s(t)和控制率u(t),使得系统状态轨迹可以从任意初始值达到切换面并保持在滑动模态附近[12].

为了方便滑模控制器的设计,定义:

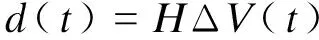
从而式(8)可以表示为:

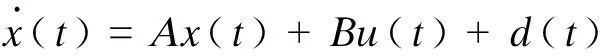
(9)

为了证明的需要,给出如下假设:

假设1存在已知的正函数β(t),使得‖d(t)‖≤β(t),‖*‖表示欧几里德范数;

假设2系统矩阵(A,B)是可控的.

2.1切换面设计

针对式(9)设计切换面s(t)满足方程:

s=Cx

(10)

其中切换增益矩阵C∈R2×5由极点配置[13]得到,选择矩阵C使得矩阵CB非奇异.

式(8)已经是简约型,故系统的状态方程展开后可以转换为:

(11)

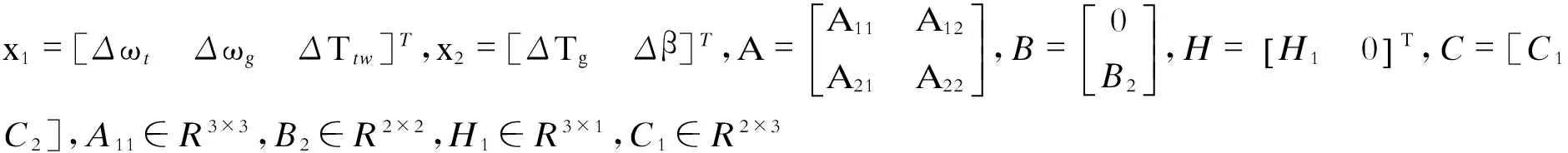
当系统到达滑模模态时,切换函数满足下列条件:

(12)

因此,系统滑模方程可以表示为:

(13)

由系统的性质可知,如果(AB)可控,(A11A12)是可控阵对,则存在状态反馈增益K,可以对矩阵(A11-A12K)的极点进行任意配置,根据所期望的极值点,求得相应的K,使得系统滑动模态是有界稳定的.

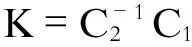
(14)

根据上述步骤,可以得到满足期望极点集的矩阵C,非奇异矩阵C2可以任取,若取C2=I,则C=[KI].

2.2系统的稳定性证明

当系统达到滑动模态时满足:

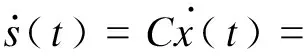
CAx(t)+CBu(t)+Cd(t)=0

(15)

可得到等效控制:

(16)

将式(16)代入式(9),得到系统滑动模态下的等价方程为:

(17)

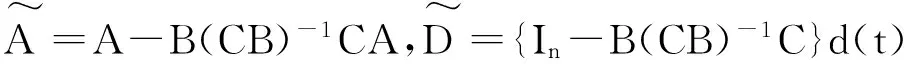
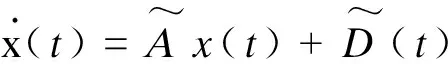
(18)

构造李雅普诺夫函数:

(19)

对v(t)求导并将式(18)代入,得:

(20)

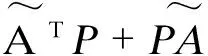
Q——给定的正定对称矩阵.

式(20)可归纳为:

因为λmin(Q)>0,由定理1可知,对于所有的t,当x∈Bc(η)时,系统是稳定的.其中,Bc(η)是以x=0为球心,η为半径的封闭球面B(η)的补.

2.3控制器设计

有风速波动的不确定系统方程(9)满足假设,利用指数趋近律[13]设计变结构控制器:

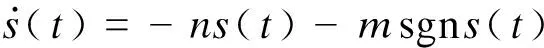
(21)

式中:n,m——正常数;

sgn——符号函数.

定理2若设计滑模控制器满足方程:

(22)

则系统满足到达条件.

证明由式(10)和式(21)可得:

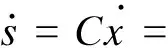
C{Ax+Bu+d}=-ns-msgns

(23)

滑模控制系统框图如3所示.假设所有状态变量可直接测量,实际应用时可通过设计状态观测器获得[1].

图3　滑模控制系统示意

3　实验仿真和结果分析

3.1高风速下变速变桨距风力发电系统与变桨距风力发电系统的仿真分析对比

为了更好地说明高风速下变速变桨距(VSVP)风力发电系统的优越性,本文利用PI控制对两者进行了仿真对比.VSVP是两个独立调节发电机功率和速度的分散PI控制器,如图4所示.

变桨距(VS)只对桨距角进行PI控制,转矩保持为额定值不变.功率控制器的参数为:Kp=0.000 08,Ki=0.000 05.转速控制器的参数为:Kp=500,Ki=67.PI控制器参数的调节运用Ziegler-Nichols整定方法[12].

图5为VSVP与VS风力发电系统仿真结果对比(截取时间为100～200 s).仿真风速为如图2所示的平均风速为20 m/s的随机波形.由图5中4个参数的输出比较可以看出,变速变桨距系统在保持输出功率(图5b)平滑稳定的同时,可以明显降低转速(图5a)波动,同时对传动系统扭转力矩(图5c)的输出波动也起到了一些平滑效果.因此,VSVP可在保证风电电能质量的情况下抑制转速和扭动转矩的波动,较单独的变桨距系统对风速的变化扰动具有更好的鲁棒性.

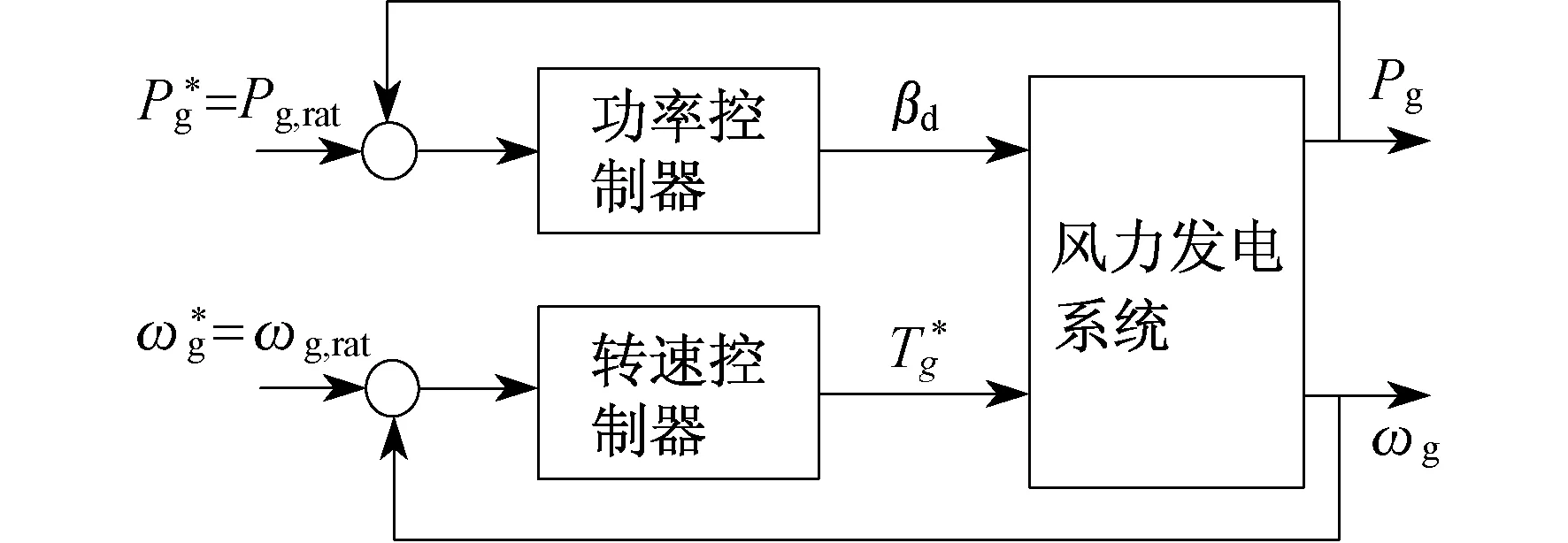
图4　高于额定风速的控制方案

3.2高风速下变速变桨距风力发电系统SMC与PI的仿真分析对比

滑模控制器的参数为:

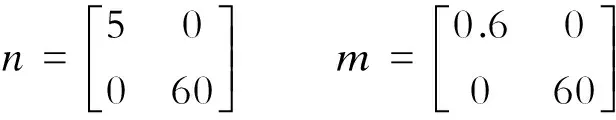
风速仍为如图2所示的平均风速为20 m/s的随机波形.图6为滑模和PI控制器的仿真结果对比(截取时间为100～200 s).由图6可以看出,滑模控制器在发电机转速(图6a)与PI控制器相差不大的同时,输出功率(图6b)更加平缓,而且传动系扭转力矩(图6c)的波动也明显减少.桨距角变化率(图6d)均在系统需求范围内,但相比PI控制,SMC控制策略下的桨距角变化率较平缓且没有突出尖峰.

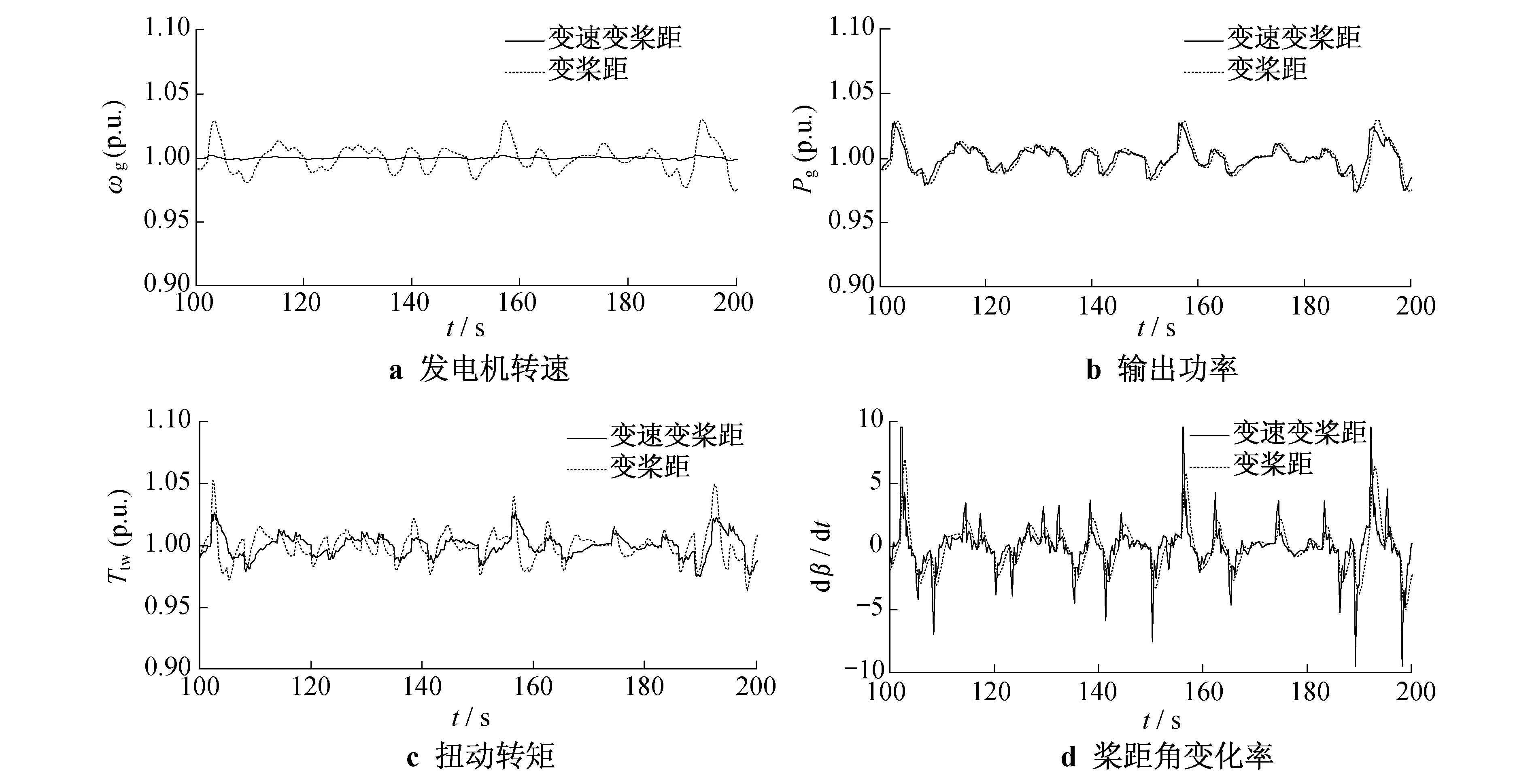
图5　VSVP与VS风力发电系统仿真结果对比

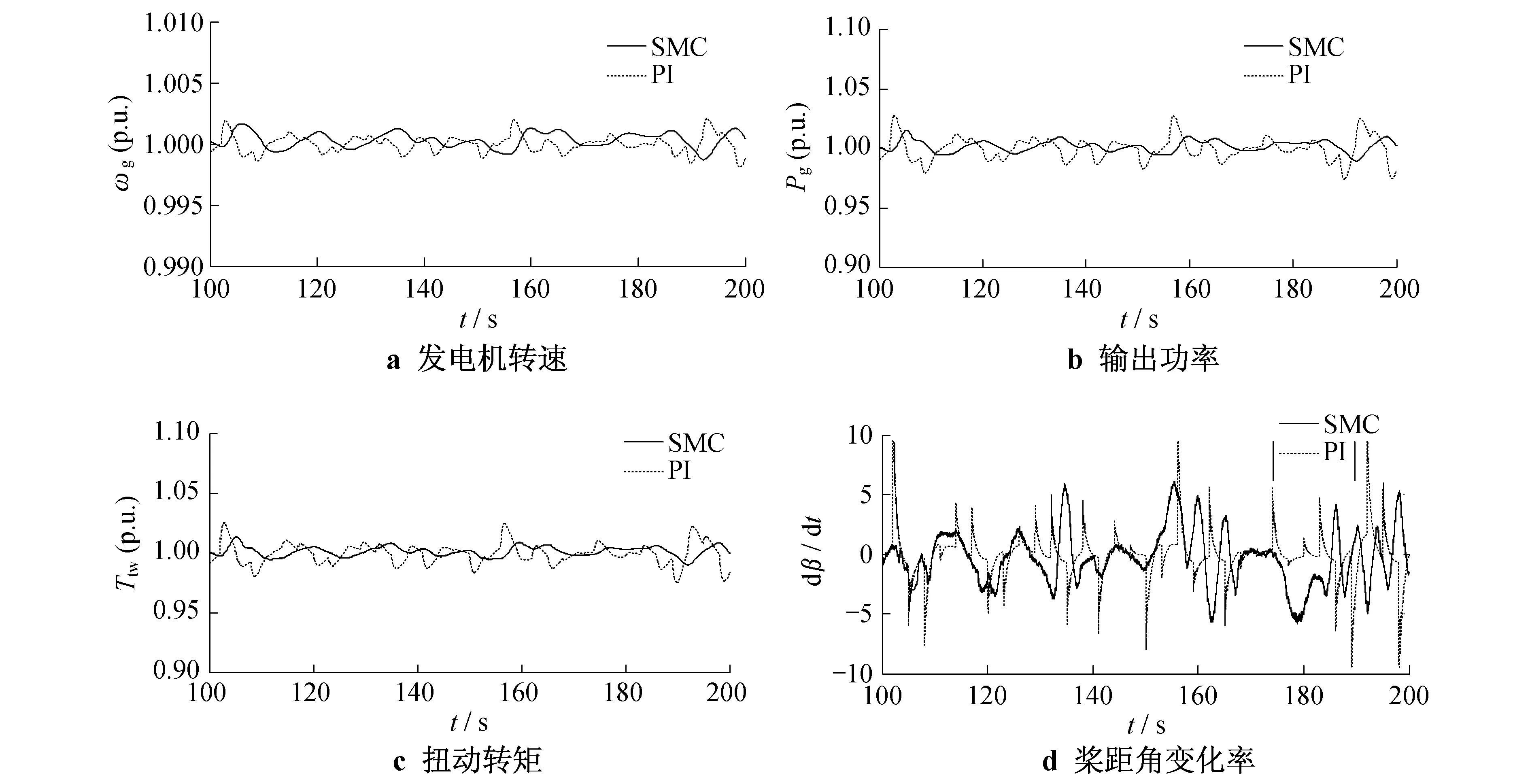
图6　系统滑模和PI控制器的仿真结果对比

由此表明,SMC控制策略下的风电系统,在维持风电系统输出功率有更好稳定性的同时,传动系统扭转力矩波动和桨距角活动频率都有所降低,不仅提高了风电能质量,而且有效地减少了桨距角系统的疲劳度和机械系统的压力,减小部件间的摩擦,有助于延长系统机械部分的寿命,降低故障的发生率.而且滑模控制桨距角的变化率变小,却没有影响风电系统功率的输出特性.

4　结　语

本文针对高风速下的风力发电系统提出了一种基于滑模控制技术的多变量控制策略.该方法根据系统在工作点附近的多变量线性化模型,基于极点配置方法设计线性切换函数,并采用指数趋近律的方法设计控制率.从仿真结果可以看出,基于变速变桨距的多变量控制策略能够更好地满足对于系统转速、转矩及功率等多个目标的平滑效果.另外,相比传统的PI控制器,滑模控制器在功率平滑和发电机的转速之间达到了较好的平衡,同时降低了传动系扭转力矩波动和变桨距执行机构的活动,并且在保持良好性能的同时,还可以保持系统的变量在安全操作范围内,这对改善电能质量及增加系统机械部分的使用寿命都产生了很好的效果.

[1]叶杭.风力发电机组的控制技术[M].北京:机械工业出版社,2011:132-189.

[2]BOUKHEZZARA B,LUPUA L,SIGUERDIDJANEA H,etal.Multivariable control strategy for variable speed variable pitch wind turbines[J].Renewable Energy,2007,32(8):1 273-1 287.

[3]CAMBLONG H.Digital robust control of a variable speed pitch regulated wind turbine for above rated wind speeds[J].Control Engineering Practice,2008,16(8):946-958.

[4]肖帅,杨耕,耿华.抑制载荷的大型风电自己滑模变桨距控制[J].电工技术学报,2013,28(7):145-150.

[5]BOSSANYI E A.The design of closed loop controllers for wind turbines[J].Wind Energy,2000,3(3):149-163.

[6]MUHANDO E B,SENJYU T,YONA A,etal.Disturbance rejection by dual pitch control and self-tuning regulator for wind turbine generator parametric uncertainty compensation[J].IET Control Theory Appl.,2007,1(5):1 431-1 440.

[7]LESCHER F,ZHAO J Y,BORNE P.Robust gain scheduling controller for pitch regulated variable speed wind turbine[J].Studies in Informatics and Control,2005,14(4):299-315.

[8]SOLIMAN M,MALIK O P,WESTWICK D T.Multiple model MIMO predictive control for variable speed variable pitch wind energy conversion systems[J].IET Renewable Power Generation,2010,2(5):124-130.

[9]秦斌,周浩,杜康,等.基于RBF网络的风电机组变桨距滑模控制[J].电工技术学报,2013,28(5):37-41.

[10]SARAVANAKUMAR R,JENA D.Validation of an integral sliding mode control for optimal control of a three blade variable speed variable pitch wind turbine[J].Electrical Power and Energy Systems,2015,69:421-429.

[11]王耀南,孙春顺,李欣.用实测风速校正的短期风速仿真研究[J].中国电机工程学报,2008,28(11):94-100.

[12]朱海锋.PID控制器参数自整定方法研究[D].广州:中山大学,2005.

[13]高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996:90-149.

(编辑胡小萍)

Study of Variable Speed Variable Pitch Controller for WindPower Generation Systems Based on Sliding Mode Control

ZHU Yinzhu, MI Yang, YANG Huixia

(School of Electrical Engineering, Shanghai University of Electric Power, Shanghai200090, China)

To improve the dynamic performance in the operation region of constant power output,multivariable control strategy using a sliding mode control technique is proposed by the reaching law method,adding the generator torque as the other control variable of wind power generation system with blade pitch angle to be controlled simultaneously.The addition of generator torque control can not only guarantee generator power and generator speed stable around its rated value,but minimize torsional torque fluctuations in the drive train and pitch actuator activity,and improve the quality of the electrical power and reduce the pressure of the mechanical parts of the system at the same time.Multivariable and monovariable control strategy under high wind speed are simulated on Matlab,the comparison results highlight the advantages of multivariable control strategy.The performance of the proposed SMC strategy is simulated and compared with PI control method,verifying the validity of control algorithm.

wind power generation system; variable speed variable pitch; sliding mode control

10.3969/j.issn.1006-4729.2016.03.013

2015-11-25

简介：朱银珠(1991-)，女，在读硕士，安徽宿州人.主要研究方向为风力发电系统的建模与控制.E-mail:578861692@qq.com.

上海绿色能源并网工程技术研究中心项目(13DZ2251900).

TM614

A

1006-4729(2016)03-0267-07