基于遗传模拟退火算法的最大功率点跟踪研究

王亚楠, 康英伟, 郑鹏远, 彭道刚

(1.上海电力学院, 上海　200090; 2.上海发电过程智能管控工程技术研究中心, 上海　200090)



基于遗传模拟退火算法的最大功率点跟踪研究

王亚楠1,2, 康英伟1,2, 郑鹏远1,2, 彭道刚1,2

(1.上海电力学院, 上海200090; 2.上海发电过程智能管控工程技术研究中心, 上海200090)

通过分析太阳能光伏发电系统的工作特征和现有的最大功率点跟踪(MPPT)方法,提出了一种基于遗传模拟退火算法的光伏发电系统MPPT方法.该算法将遗传算法和模拟退火算法相结合,通过将局部搜索过程引入遗传算法,从而使两种算法的搜索能力得到互相补充.针对某光伏发电系统的MPPT问题,通过仿真,将遗传模拟退火算法和遗传算法进行比较.仿真结果显示,遗传模拟退火算法和传统的遗传算法相比,能更快速、精确地跟踪到光伏系统的最大功率点.

光伏发电; 最大功率点跟踪; 遗传模拟退火算法

太阳能取之不尽、用之不竭,光伏电池可以将资源无限、清洁干净的太阳辐射能转换为电能,因此太阳能光伏发电技术成为新能源和可再生能源技术的重要发展方向[1].由于光照强度和环境温度是变化的,光伏电池的输出电压也会随之变化,但是在某一时刻光照强度和环境温度确定时,某一特定的输出电压值使得光伏电池的输出功率达到最大.因此,为了有效提高光伏电池的使用效率,需要通过控制技术实现光伏发电的最大功率点跟踪(Maximum Power Point Tracking,MPPT).

目前,最大功率点跟踪的传统方法有功率扰动观察法、增量电导法、爬山法和间歇扫描法等[2],但都存在一些不足,如系统在最大功率点附近会产生振荡、步长的选择会影响跟踪的速度以及动态跟踪精度不高等[3].此外,还有一些智能优化方法,如模糊控制、神经网络[4]、遗传算法等.虽然目前智能方法还存在理论不够成熟、实时性欠缺等问题,但其具有动态和稳态性能较好、可明显改善光伏系统的跟踪速度及有效减弱环境因素对光伏阵列的影响等优点.随着MPPT方法研究的逐步深入,智能方法的应用也会越来越普遍[5].

遗传算法(Genetic Algorithm,GA)是一类以Darwin自然进化论与Mendel遗传变异理论为基础的、具有自适应能力的、全局性的概率搜索算法[6].在最大功率点跟踪中,使用遗传算法,能够快速有效地搜索到最大功率点.但对于复杂的优化问题,它仍存在着缺点,如搜索空间大、搜索时间较长、局部搜索能力较差、易出现“早熟”收敛的情况等[7].在大型并网发电系统中,由于光伏电池板方阵占地面积可达几平方公里[8],其输出的特性曲线十分复杂,使用传统的遗传算法得到的跟踪效果难以令人满意,因此对其进行改进十分必要.

文献[9]提到模拟退火法(Simulated Annealing,SA)是一种模拟高温金属降温热力学过程的随机组合优化方法.在初始温度足够高、温度下降足够慢的条件下,能以概率1向全局最优值收敛.文献[10]提到,模拟退火算法具有较强的局部搜索能力,但它却不能使优化搜索过程进入到最有希望的区域.遗传算法的局部搜索能力较弱,但在把握搜索整体过程方面却具有优势.基于此,本文尝试结合使用这两种算法,取长补短,以求能达到更好的追踪效果.

1　光伏发电系统模型

1.1光伏电池的模型及简化

利用光伏电池的光生伏特效应原理,在一定的光照强度下,可以把每片光伏电池单元看作是一个恒流源与一只正向二极管的并联回路,其等效电路模型如图1所示.

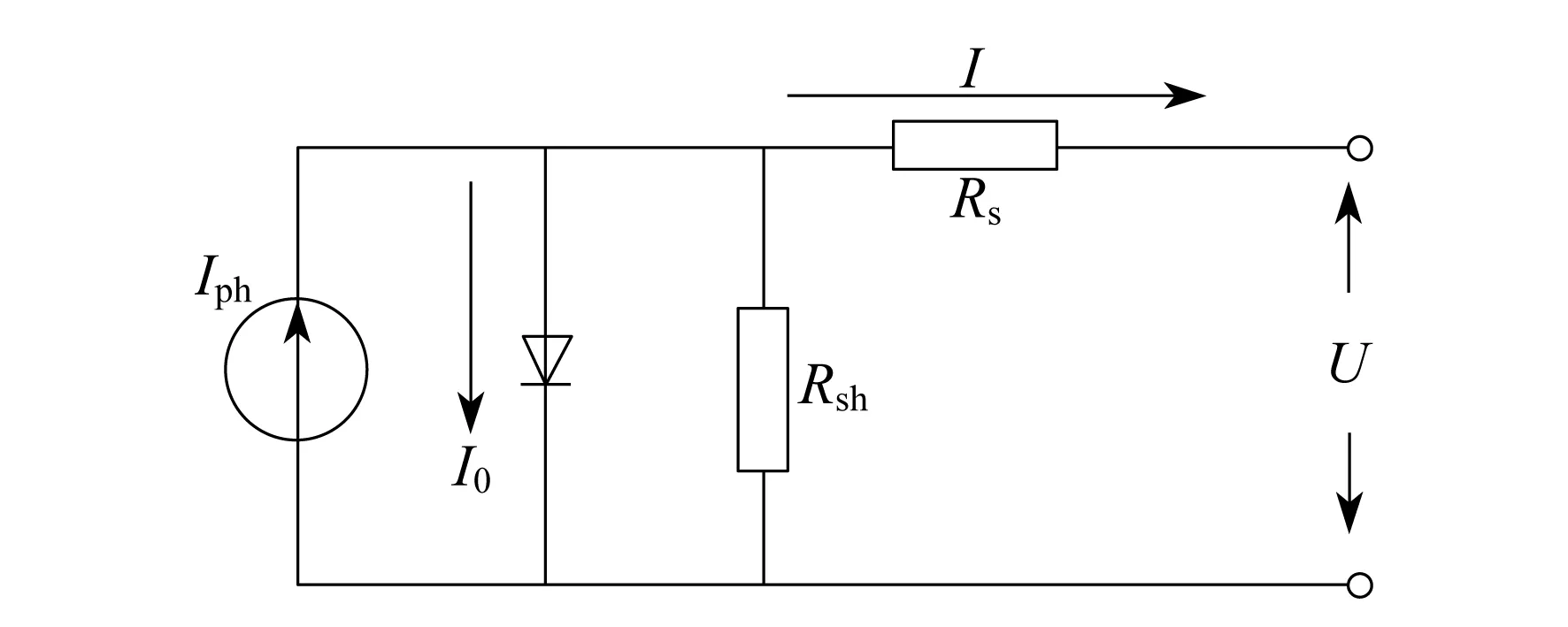
图1　光伏电池等效电路

由图1可见,由于光伏电池的电极表面层有横向电流流过,故在等值电路中应串联一个电阻Rs.Rsh为分路电阻,补偿由于PN结(PN junction)缺陷造成的漏电流I0,其方向和Iph相反.负荷电阻上流过的电流为I,则此时光伏电池的输出电流可表达为[11]:

(1)

式中:Iph——光生电流;

I0——流过二极管的反向饱和漏电流;

Rs——串联等效电阻;

Rsh——分路电阻;

U——太阳能输出电压;

q——单位电荷,q=1.6×10-19C;

k——玻尔兹曼常数,k=1.38×10-23J/K;

T——电池温度;

n——二极管指数.

Iph和I0是随环境变化的量,需要根据具体的光照强度和外界温度来确定,其计算式分别为[12]:

(2)

(3)

式中:Isc——标准日照、标准温度(光照强度为1 000 W/m2,温度为25 ℃)时的短路电流;

ht——温度系数,取6.4×10-4;

T——光伏电池的温度;

Tref——标准电池温度;

a——常数,取1.336×104;

b——常数,取整为235;

S——光照强度;

Sref——标准光照强度.

由式(2)和式(3)可知,Iph和I0难以确定,并且电池厂家提供的技术参数中并不包括这两项,因此在工程中不便于分析和利用.因此,简化光伏电池的数学模型十分必要,从而使其更利于工程的实际应用.工程用的光伏电池数学模型在式(1)的光伏电池U-I特性基础之上,做以下处理:

(1) 一般情况下,可忽略(U+IRs)/Rsh项,因其远小于光电流I;

(2) 可假设Iph=Isc,因为二极管的正向导通电阻远大于Rs.

定义最大功率点处的电压和电流分别为Um和Im.在开路状态下的电压和电流分别为Uoc和零.则此光伏电池的U-I方程可简化为:

(4)

可解得:

(5)

(6)

日照强度和电池温度改变时,再次计算Isc,Uoc,Im,Um.然后求出C1和C2,即得新的U-I特性曲线[13]如下:

(7)

(8)

(9)

(10)

(11)

(12)

式中:d——常数系数,取0.002 5 (℃)-1;

g——常数系数,取0.5;

h——常数系数,取0.002 88 (℃)-1;

DS,DT——光照强度和温度的变化量;

Uoco,Isco——开路电压和短路电流的初始值;

Imo,Umo——最大功率点处电流和电压的初始值.

在此选用文献[14]中的光伏电池的电气参数:最大功率点处电压Um选为19.2 V,电流Im选为5.32 A,开路电压Uoc选为22.6 V,短路电流Isc选为5.67 A.外界条件如下:温度为25 ℃,光照强度在200～1 000 W/m2之间.得到光伏电池的电流-电压和功率-电压输出特性曲线,如图2所示.

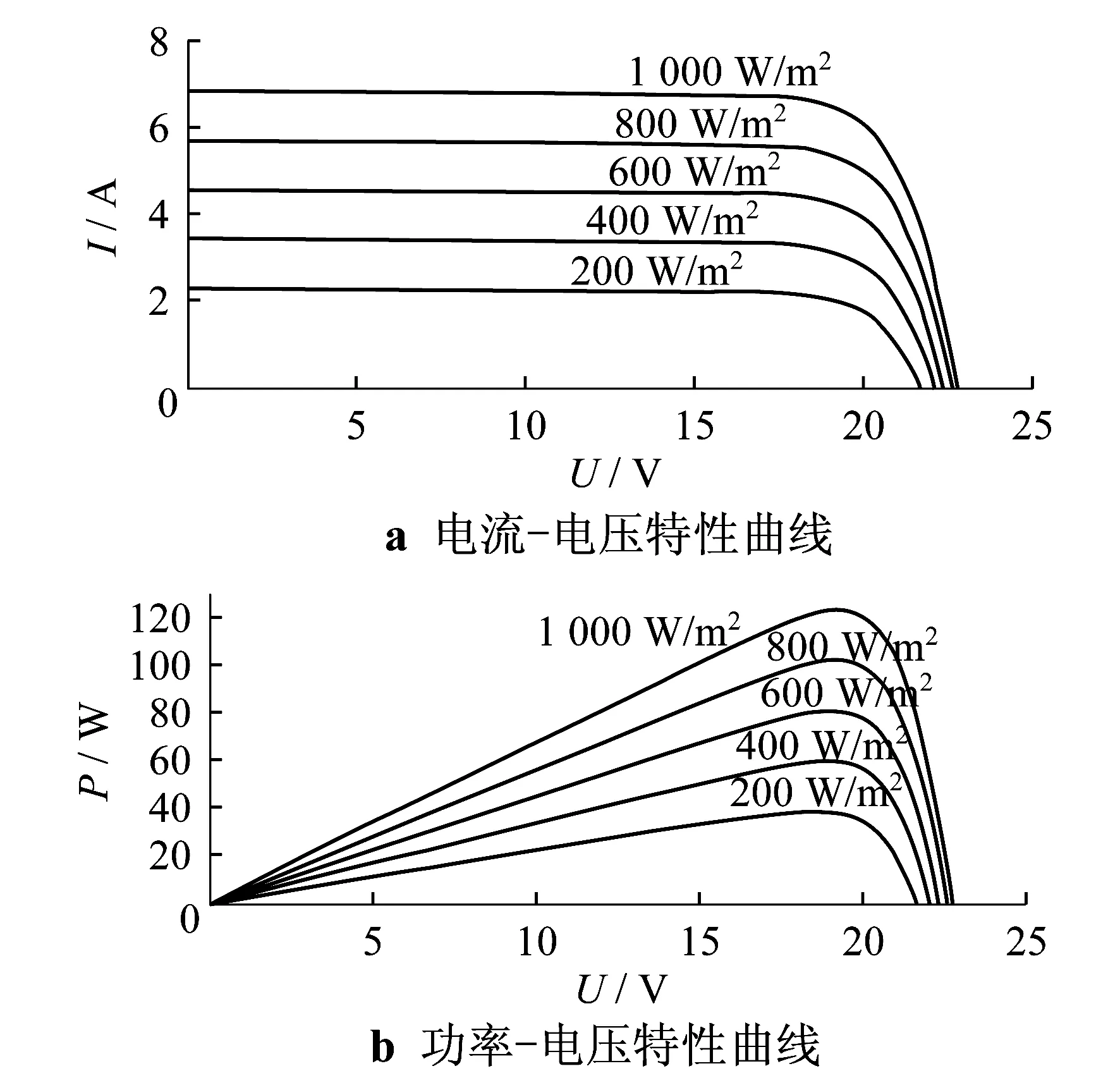
图2　光伏电池仿真输出曲线

由图2可知,光伏电池的U-I特性表现出很明显的非线性,这是由于受到光伏电池自身内部模块结构等参数及外界环境因素的影响所致.分析光伏组件的输出特性可得出:当电压取值较低时,光伏电池具有恒流源特性,而在接近开路电压UOC时,光伏电池则表现出恒压源的特性;随着光照的增强增大,短路电流也随之增大,而开路电压则随温度的升高而降低.在光照和温度确定的工作环境条件下,光伏电池输出特性曲线上存在惟一的点M,该点即是光伏电池的最大功率输出点,其对应于功率-电压曲线的最大值点.

1.2Boost变换器模型

本文选用Boost变换器作为光伏电池板方阵的MPPT控制电路,图3为选用Boost变换器的光伏发电系统结构图.

对该变换器的状态空间模型进行线性化处理[15]后所得模型如下:

(13)

式(13)中B的计算式为:

(14)

此外

(15)

式中:D——占空比,且0≤D≤1;

U——状态变量.

当Lc和Cs的值确定后,ΔU主要由UTC的变化决定.通过调整UTC的大小就可以改变U的值.由此可知,要实现光伏发电系统输出最大功率,可以通过改变占空比D来控制光伏电池的工作点.

图3　光伏发电系统结构示意

2　基于遗传模拟退火的MPPT算法

遗传模拟退火算法[16]是从一组随机产生的初始解(初始群体)开始全局最优解的搜索过程,它先通过选择、交叉、变异等遗传操作来产生一组新的个体,然后再独立地对所产生出的各个个体进行模拟退火过程,以其结果作为下一代群体中的个体,这个运行过程被反复迭代,直到满足终止运行的条件.

本文将遗传算法和模拟退火算法相结合来进行最大功率点的跟踪.具体的思想是全局搜索过程采用改进的遗传算法来进行,使优化后的点迅速到达最大功率点区域附近,然后局部精细寻优过程采用模拟退火算法进行,直到搜索过程达到一定的精度要求为止.该算法的主要步骤如下:

(1) 设置系统初始数据和控制参数.控制参数包括初始温度T0,终止温度Te,退火系数r和总的升温次数L;

(2) 给定初始解.选取占空比D作为决策变量并进行编码,考虑到0≤D≤1,因此采用二进制编码.随机生成M个个体的初始群体P(t),令升温次数累计g1=0,并定义如下变量:操作代数v,交叉概率PC和变异概率Pm;

(3) 输出功率P=IU作为MPPT控制研究的目标函数,又因其值总为非负,在此直接将此目标函数作为遗传模拟退火算法的适应度函数,即E(X)=P;

(4) 设定控制温度初值T=T0;

(5) 对种群P(t)中的各个个体进行两两随机配对.之后对其中的每一对个体组进行交叉和变异运算,由两个父代个体p1,p2生成两个子代个体c1,c2;

(6) 对由父代个体和子代个体所组成的两个个体组,即p1和c1,p2和c2,以概率p接受父代个体为下一代群体中的个体,以概率(1-p)接受子代个体为下一代群体中的个体,替代P(t)中的原有个体.其中:

(16)

式中:fp,fc——父代个体和子代个体对应的目标函数值;

(7) 令k=k+1,并降低控制温度,令t=tr.判断是否达到终止温度Te,如果达到,则转至(8),否则转至(5);

(8) 修正升温次数,令g1=g1+1;

(9) 判断升温次数是否到达限值L,若达到则输出此时的优化结果,否则转至(4).

图4给出了该算法的执行流程.

从上述内容可知,将模拟退火算法引入到遗传算法中,在优选下一代群体中的个体时加入了一定的“扰动”来保持种群的多样性,既能加强位串之间的竞争,又能加快遗传算法的搜索速度,最终解决了遗传算法易陷入局部最优的问题,并朝着全局最优的方向搜索.遗传模拟退火算法混合策略是一种两层并行搜索的结构.内部层次上,在不同温度下混合算法串行并依次进行遗传算法和模拟退火算法的搜索,这是一种两层串行结构.外部层次上,使用遗传算法提供的并行搜索结构,使模拟退火算法转化成为并行模拟退火算法.因此,混合算法始终在进行着种群并行优化.

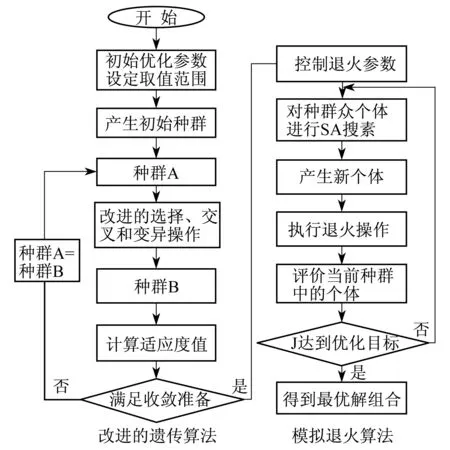
图4　GASA优化流程

3　仿真分析

分别对遗传模拟退火算法和遗传算法两种MPPT算法进行仿真,通过比较,考察新算法的性能.在Matlab/Simulink中建立仿真模型,其中MPPT控制模块采用S-函数来实现.

选用文献[17]所述的仿真模型的参数,即:Lc=6 mH,CS=45 μF,Cd=1 000 μF,负载为纯电阻负载R=100 Ω.在算法中设定占空比D的上界为1,下界为0,初始种群P(t)包含M=40个个体,操作代数v取100,精度s取0.01,交叉概率PC取0.8,变异概率Pm取0.01.初始退火温度T0设置为5,终止温度Te设置为0.005.降温系数r选为0.9.总升温次数L设置为30.算法将每一代中的最佳个体适应度即最大功率值进行保存并输出.设置工况在标准条件下,即光照强度为1 000 W/m2,温度为25 ℃.光伏电池的初始工作点为24 W,该条件下最大功率点为125 W.分别用遗传模拟退火算法和传统的遗传算法进行仿真,得到的运行结果对比图如图5所示.

通过图5中两种算法的仿真结果对比可以发现,两种控制算法都能跟踪到最大功率点,但遗传模拟退火算法的曲线跟踪速度更快,经过0.131 2 s,在第30代左右时搜索结果趋于稳定,功率达到的最大值为124.989 9 W.而传统遗传算法的曲线经过0.216 8 s,在第50代左右时搜索结果趋于稳定,功率达到的最大值为123.039 2 W.由此可见,基于遗传模拟退火算法的MPPT方法在速度和精度上具有更好的跟踪效果.

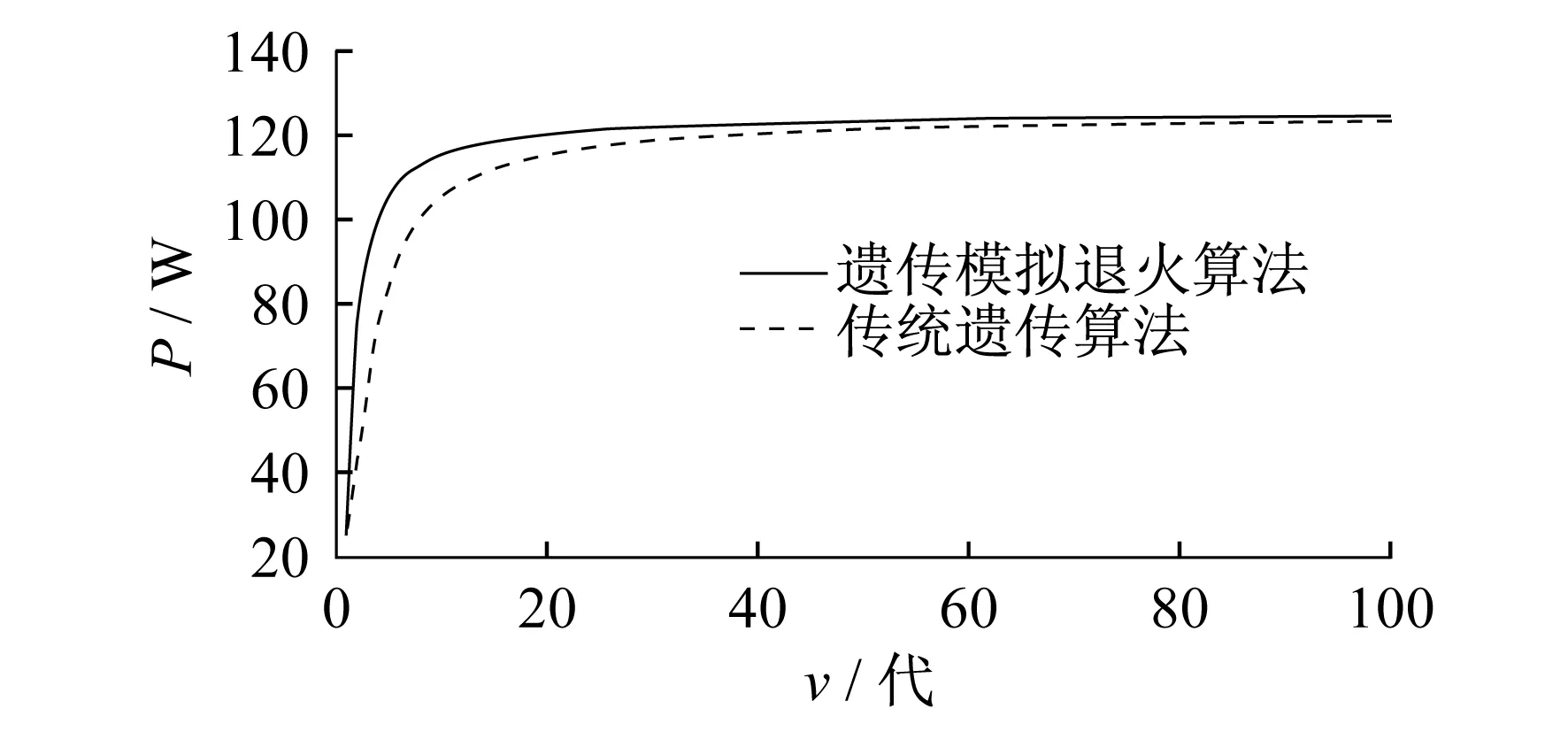
图5　两种算法仿真结果对比

4　结　语

本文将遗传算法和模拟退火算法相结合提出了一种新的MPPT算法,并通过仿真,将其和遗传算法进行比较,验证了设计前的预想,即:遗传模拟退火算法通过逐步保留更优解,使得每一代运行结果优于上一代,在误差允许的范围内,可以用较少的遗传代数获得满意的结果,节约运行时间,使得种群更快地搜索到全局最大功率点.与传统的遗传算法相比,在快速和精确上有了一定的提高.

[1]李安定,吕全亚.太阳能光伏发电系统工程 [M].北京:化学工业出版社,2012:156-160.

[2]高林.基于遗传算法的最大功率点跟踪[J].控制工程,2012,6(4):5.

[3]周林,武剑,栗秋华,等.光伏阵列最大功率点跟踪控制方法综述[J].高电压技术2008,34(6):1 145-1 154.

[4]石俊,陈丁.改进的光伏发电系统MPPT预测算法的研究[J].计算机仿真,2014,31(11):127-131.

[5]程启明,程尹曼,汪明媚,等.光伏电池最大功率点跟踪方法的发展研究[J].华东电力,2009,8(37):1 300-1 305.

[6]边霞,米良.遗传算法理论及其应用研究进展[J].计算机应用研究,2010,7(27):2 425-2 439.

[7]葛继科,邱玉辉,吴春明,等.遗传算法研究综述[J].计算机应用研究,2012,5(10):6-11.

[8]佘世杰,何慧诺.光伏水泵系统中CVT及MPPT控制比较[J].太阳能学报,2006,33(6):25-31.

[9]王彦,王超,刘宏立.模拟退火遗传算法在多用户检测技术中的应用[J].电子技术应用,2011,37(4):102-105.

[10]艾芊.现代电力系统辨识人工智能方法 [M].上海:上海交通大学出版社,2012:363-364.

[11]李丽芳,江冰,吉正洵,等.光伏发电系统MPPT控制仿真模型[J].计算机仿真,2015,32(4):116-120.

[12]刘东冉,陈树勇,马敏,等.光伏发电系统模型综述[J].电网技术,2011,35(8):47-52.

[13]王长江.基于MATLAB的光伏电池通用数学模型[J].电力科学与工程,2009,25(4):11-15.

[14]杨金孝,朱琳.基于Matlab/Simulink光伏电池模型的研究[J].现代电子技术,2011,34(24):192-195.

[15]王岩.光伏发电系统MPPT控制方法的研究[D].北京:华北电力大学,2007.

[16]陈小平,顾雪平.基于遗传模拟退火算法的负荷恢复计划制定[J].电工技术学报,2009,24(1):171-176.

[17]张锋,惠晶.基于极值搜索算法的光伏系统MPPT控制[J].电力电子技术,2014,48(2):6-9.

(编辑桂金星)

Research of Maximum Power Point Tracking Based on Genetic Simulated Annealing Algorithm

WANG Yanan1,2, KANG Yingwei1,2, ZHENG Pengyuan1,2, PENG Daogang1,2

(1.Shanghai University of Electric Power, Shanghai200090, China; 2.Shanghai Engineering Research Center of Intelligence Management and Control for Power Process, Shanghai200090, China)

By analyzing the working characteristics of the solar photovoltaic power generation system and the Power Point Tracking Maximum(MPPT)method,a new MPPT method based on genetic simulated annealing algorithm is proposed.The algorithm combines genetic algorithm and simulated annealing algorithm,and the local search process is introduced into genetic algorithm so that the search ability of the two algorithms is complementary to each other.For the MPPT problem of a photovoltaic power generation system,through simulation,the genetic simulated annealing algorithm results are compared with the simulation results of genetic algorithm.The simulation results show that compared with the traditional genetic algorithm,the genetic simulated annealing algorithm can track the maximum power point of the PV system quickly and accurately.

photovoltaic power generation; maximum power point tracking; genetic simulated annealing algorithm

10.3969/j.issn.1006-4729.2016.03.010

2015-09-29

简介：王亚楠(1990-),男,在读硕士,山东泰安人.主要研究方向为光伏发电,微电网技术.E-mail:wangyanan1990@126.com.

上海市自然科学基金(15ZR1418600); 上海市科学技术委员会工程技术研究中心资助项目(14DZ2251100).

TM615.2;TP13

A

1006-4729(2016)03-0252-05