航空倾斜摄影系统多相机姿态安装误差检校
冯雁飞,张云生 ,杜守基
(中南大学 地球科学与信息物理学院,湖南 长沙 410083)
航空倾斜摄影系统多相机姿态安装误差检校
冯雁飞,张云生 ,杜守基
(中南大学 地球科学与信息物理学院,湖南 长沙 410083)
针对航空倾斜摄影系统多相机间相对关系的姿态误差,提出一种利用下视影像密集匹配点云约束的联合平差多相机姿态安装误差检校方法。文中方法以共线方程为基础,通过联立倾斜立体像对连接点、下视影像密集匹配点云数据提供的高程约束虚拟观测值,采用非线性最小二乘SQPM算法求解倾斜影像的外方位元素改正数,从而解算下视相机与倾斜相机间的姿态安装误差。为了保证连接点可靠性,提高虚拟观测值的有效性,采用下视影像密集匹配的点云约束倾斜影像立体连接点匹配和分布优化过程。利用SWDC-5倾斜摄影系统获取的数据进行实验,通过原始姿态检校参数将下视影像生成的密集点云投影至倾斜立体影像上,在像方有22个像素左右的误差,采用文中方法检校后,像方误差减少到0.29个像素。
航空倾斜摄影系统;检校;联合平差;SQPM算法
倾斜航空摄影的出现改变了传统摄影测量方式,为我们提供了更详尽的多角度空间影像信息[1-3]。倾斜航空摄影技术采用5个镜头同时获取下、前、后、左、右5个方向影像数据,外加GPS/IMU系统获取下视相机的空间位置和姿态信息,其他4个相机的姿态和方位可以通过相机间的相对安装关系推理[4-5]。但下视相机和倾斜相机在飞行过程中,有可能存在曝光不同步,以及受到安装工艺的影响,易导致相机之间的关系检校参数存在一定的误差,从而影响后续的三维建模或者纹理映射等工作[6]。
传统的安装误差检校,主要针对下视相机和POS系统之间的安装误差,可以采用检校场进行检校;或者在平差过程中,在控制点约束下,顾及这个安装误差,利用POS数据辅助的光束法平差来进行检校[7-8]。在检校场数据有限的情况下,如果有激光点云等辅助数据,可以使用激光扫描数据来检校安置角误差,达到配准激光点云数据和同步影像的目的[9-10]。
当前的摄影测量系统处理倾斜摄影系统获取的下视影像的技术和工艺已日趋成熟,因此,本文以下视影像自动空三的结果为基础,采用密集匹配方法获取下视影像密集点云,然后以该点云为约束条件,通过联合平差的方法检校下视影像和倾斜影像之间的安装误差。
1 基于联合平差的检校方法
1.1检校流程
本文基于联合平差的检校流程如图1所示,一共分为以下3个步骤:
1) 下视影像密集匹配点云约束的倾斜影像立体像对SIFT匹配。首先通过SIFT匹配获取重叠区域的同名点[11],然后利用 RANSAC 算法剔除可能的错误匹配点[12]。
2) 同名点分布优化。根据联合平差的要求,对同名点的分布进行优化。
3) 联合平差。构建误差方程,采用最小二乘间接平差原理进行平差迭代求解参数,实现下视影像与倾斜影像间相对位置关系的检校。
1.2联合平差模型
本文联合平差模型的误差方程包括如式(1)所示的两类误差方程。
(1)

1.3SQPM算法
非线性函数的经典最小二乘平差是用线性函数模型的方法把非线性函数在参数的概略值处对其进行泰勒级数展开,忽略高次项后按照最小二乘法求解。该方法的局限性在于参数的概略值必须接近参数的平差值[13],否则线性化过程中存在着难以忽略的模型误差,造成求解参数不在真实值附近收敛或者造成发散,难以求解。
SQPM(SequentialQuadraticProgrammingMethod,序列二次规划方法) 算法[14,15]又称为基于二次规划的投影Lagrange方法,是一种带约束极值算法。SQPM的Hesse矩阵恒等于2P,为常数阵,无需迭代进行修正计算,采用SQPM算法求解时避开了棘手的修正Hesse矩阵的繁琐计算。数学模型为
(2)
该模型对概率值的要求只要是在参数平差值邻近较宽的连续、平滑、单调、可微区间内的任意一点Xk处。
(3)
1.4高程约束
对于下视影像密集匹配生成的点云数据内插出的DSM(Digital Surface Model),若下视相机与倾斜相机间相对关系不含误差,则利用共线方程前方交会求出的连接点物方坐标应该和利用下视影像匹配得到点云生成的DSM内插物方坐标的高程值在误差范围内接近。由于相对关系存在误差,导致由下视影像外方位元素以及相对关系推导的倾斜影像初始外方位元素不准确,从而倾斜影像前方交会求出的高程值和下视影像密集匹配点云生成DSM内插求出的高程值存在较大差值。本文方法以这个高程的差值作为虚拟观测,实现平差后倾斜影像连接点的高程值接近下视影像密集匹配点云DSM内插的高程。
如图2所示,L,R为倾斜相机的影像,V点云是下视影像密集匹配得到的点云,同名点x-x′对应的物方点为A(X,Y,Z)。若倾斜影像外方位元素准确,则A点的高程应该等于周围点云内插出的高程Zinter,即
(4)
由于倾斜影像的外方位元素存在误差,因此,式(5)改写为误差方程式为
(5)
式(5)即为密集匹配点云高程约束的虚拟观测方程,Z0为倾斜影像连接点使用初始外方位元素前方交会计算的初始高程值。当连接点位于建筑物边缘或植被区域时,内插的高程精度会下降。由于采用了连接点前方交会的高程和内插的高程值作为虚拟观测,因此,为了保证虚拟观测能够正确约束联合平差,本文只选择位于点云分布平滑区域内的同名点作为平差的连接点。
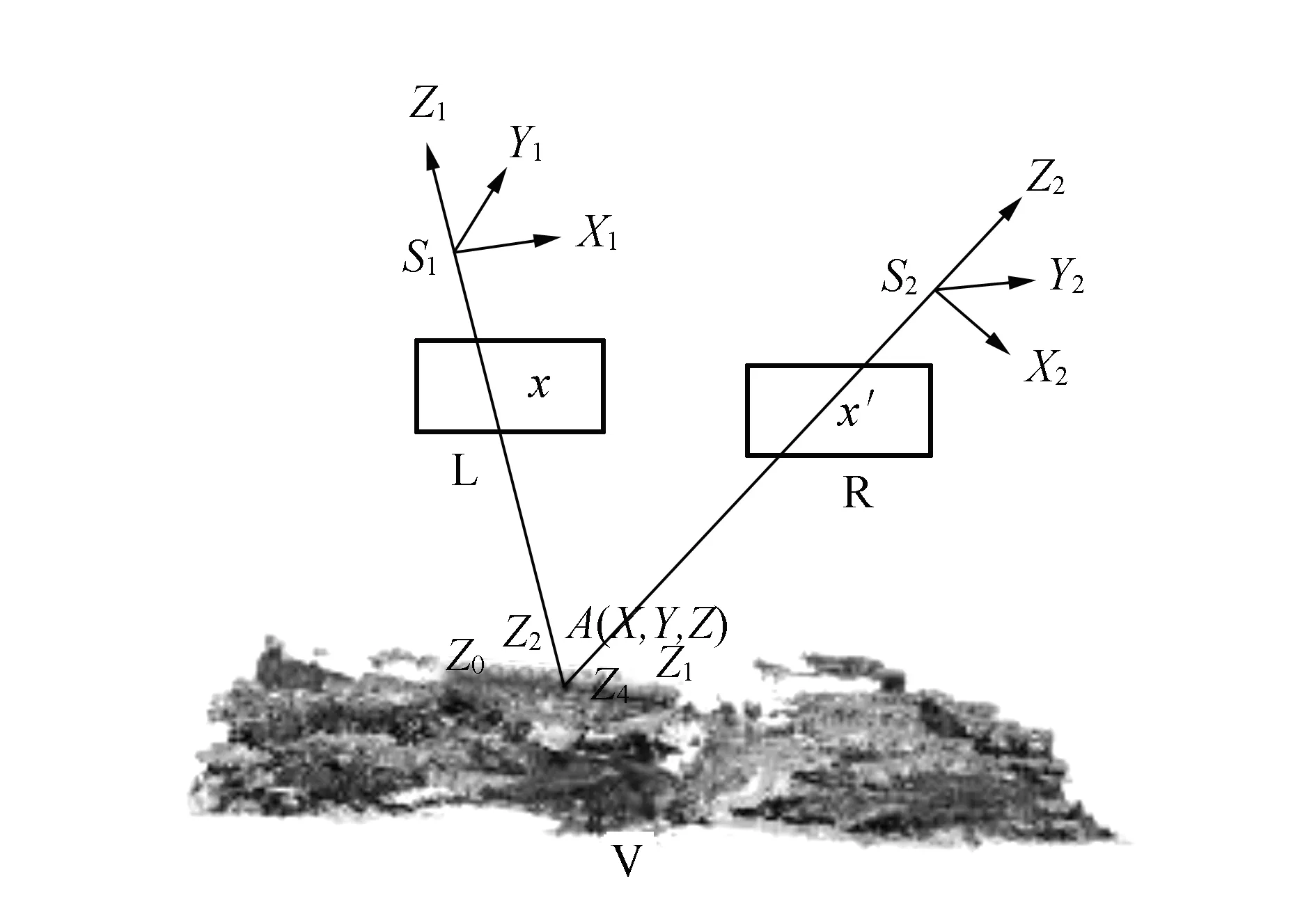
图2 点云高程约束
1.5点云辅助的SIFT特征匹配与优化
连接点的提取和优化是本文基于联合平差进行数字影像和点云配准的关键所在,手工量测同名点往往耗费大量的时间。经典SIFT匹配不仅耗时,而且分布受到纹理的影响,不符合本文连接点的要求。因此,本文利用点云来约束SIFT特征匹配主要步骤如下:
1) 将点云数据投影至立体影像上,根据投影点计算立体影像的重叠区域。
2) 在立体影像上的重叠区域提取立体影像的SIFT特征点并进行匹配,并且采用双向匹配法进一步保证匹配可靠性。
3) 基于相对定向的误差剔除。虽然基于SIFT的特征点匹配能够取得大量的同名点,并且经过双向匹配后,错误匹配得到很大程度抑制,但依然存在有少量的错误匹配,因此,本文结合RANSAC算法以及立体像对的核线几何约束,计算基础矩阵,来过滤掉可能的错误匹配[10]。
4) 同名点优化。本文联合平差需要的同名点周围应有大量的点云,才能保证每次迭代结果落在可靠区域。因此,检查初始同名点以R(实验中R取50个像素)为半径的圆形区域内是否存在一定数目点云,并且点云的高程标准差是否小于阈值δ(δ取0.1 m)。由于不确定系统误差的分布情况,因此,在检查周围点的分布时,同名点周围的4个象限都需要有激光点云存在。通过以上步骤,筛选出合适的同名点后,再在每个均匀格网中选择一个同名点作为最后参与平差的连接点。
1.6权值确定
式(1)中,连接点可以认为是等权观测,因此,P1设为单位矩阵。方程2有强制约束作用,它能够让前方交会求出的三维点高程的Z值强制约束至它的理论真实值位置,通过多次迭代,进一步约束,最终使前方交会求出的高程值逐步和真值接近。根据先验权值和具体实验得出方程2的权值P2比方程1的权值P1大2个数量级方程能够更好地收敛。
2 实验与分析
2.1实验数据
为了验证本文方法,本文采用了SWDC-5系统获取的影像进行实验,该系统下视E相机的主距50.688 mm,选用的C相机的主距是82.252 mm,像元大小6.0 μm。图3(a) 为下视影像经过密集匹配得到的点云数据,图3(b)和图3(c)为C相机所获得的一个倾斜立体像对。密集匹配的点云数据一共有32,383,134个点,相机参数经过了严格检校,影像已经过畸变差改正和主点平移,影像大小为8 176像素×6 132像素。
为了便于后续结果分析,用CloudCompare点云处理软件人机交互的方式选择如图4所示的3个的数据块。其中图4(a)描述了3个数据块在影像上的大致区域,图4(b)、(c)、(d)分别为选择的数据块点云Ⅰ、Ⅱ、Ⅲ的示意图。标记区域Ⅰ位于平坦的地面,标记区域Ⅱ位于不规则的楼顶,标记区域Ⅲ位于棚状弧形结构的楼顶。通过选择3种不同位置、不同结构的点云数据块,旨在证明本方法的有效性。

图4 标记区域点云
2.2连接点提取结果
对图3(b)、(c)所示的立体像对,利用SIFT单向匹配共匹配出2 778对同名点,经过双向匹配剔除了454对同名点,剩余2 324对同名点。利用RANSAC方法剔除可能错误的匹配后,剩余1 817对同名点,结果如图5所示。
在匹配的基础上,保留同名点周围40个像素以内、4个象限都有下视影像密集匹配点云投影点,且这些点的高程标准差小于0.2 m的同名点,余下107对同名点。经过格网分布优化之后,最终保留32对同名点,图6为最终同名点分布图。

图5 RANSAC后同名点
2.3检校结果
为了验证检校结果,将图4(b)、(c)、(d)所示的点云采用检校前和检校后的外方位元素数据分别投影至倾斜影像上,得到的结果如图7所示。其中,检校之前的结果采用红色点标记,检校后的投影结果采用绿色点标记。从图7可以看出,检校之前,投影点与影像的屋顶套合存在误差,约为23个像素大小的偏移。检校之后,从绿颜色的投影结果可以看出,点云投影结果和影像严格套合,且在左右影像都能严格套合,表明本文方法的可行性。

图6 连接点分布优化结果





图7 检校前后对比
图7可以明显地发现无论左右影像,经过检校后,下视影像密集匹配点云可以投影到倾斜立体像对的相应位置上。
2.4精度验证与分析
为了进一步验证本文方法,在下视密集匹配点云数据辅助下,通过人机交互的方式,在倾斜立体像对上选择了19对同名点。然后比较利用检校前后的外方位元素前方交会的高程与点云数据内插高程的差值dZ,以及前方交会后,将三维点投影至原始立体影像上分别计算至左右影像的投影差dl和dr,并统计最大值max,最小值min以及均方误差rmse,结果如表1所示。从表1可以看出,检校前,检查点在左影像上的投影误差最大值为24个像素,最小值为20个像素,均方根误差为22个像素;在右影像上的最大投影误差为26个像素,最小值为19个像素,均方根误差为23个像素;检查点的高程误差均方误差为2.436 m。采用本文方法进行检校,左影像的投影误差均方差仅为0.27个像素,右影像为0.36个像素,高程方向的均方误差为0.038 m。结果表明,本文方法可以有效提高精度。
2.5实验补充
为了验证本文方法的可行性,选用了SWDC-5系统D相机方向的一个立体像对做了对比实验。图8为D相机得到的立体像对,图9为用D相机的一个立体像对做实验,其中图9(a)描述了3个数据块在D相机一张影像上的大致区域,图9(b)、(c)、(d)分别为选择的数据块点云Ⅰ、Ⅱ、Ⅲ的示意图。

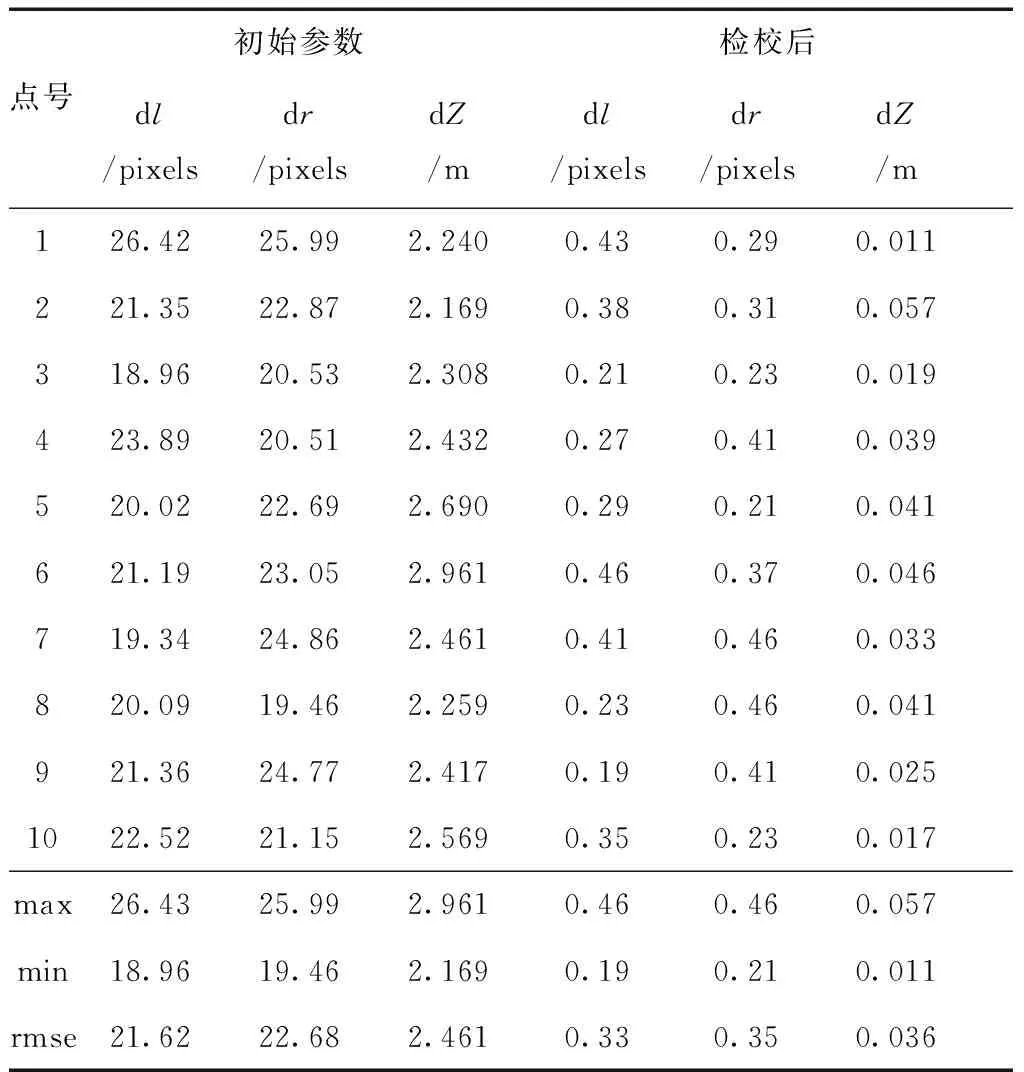
表1 结果对比

图8 实验数据
通过图10的左右影像检校前后投影对比图,可以发现该方法在D相机方向的立体像对经过检校后取得了理想的投影结果。 对D相机立体像对实验结果进行精度分析,从表2可以看出,检校前,检查点在左影像上的投影误差最大值为26个像素,最小值为19个像素,均方根误差为21个像素;在右影像上的最大投影误差为26个像素,最小值为19个像素,均方根误差为23个像素;检查点的高程误差均方误差为2.461 m。采用本文方法进行检校,左影像的投影误差均方差仅为0.33个像素,右影像为0.35个像素,高程方向的均方误差为0.036 m。

图9 标记区域点云






图10 检校前后对比
点号初始参数检校后dl/pixelsdr/pixelsdZ/mdl/pixelsdr/pixelsdZ/m126.4225.992.2400.430.290.011221.3522.872.1690.380.310.057318.9620.532.3080.210.230.019423.8920.512.4320.270.410.039520.0222.692.6900.290.210.041621.1923.052.9610.460.370.046719.3424.862.4610.410.460.033820.0919.462.2590.230.460.041921.3624.772.4170.190.410.0251022.5221.152.5690.350.230.017max26.4325.992.9610.460.460.057min18.9619.462.1690.190.210.011rmse21.6222.682.4610.330.350.036
3 结 论
针对航空倾斜摄影系统下视相机与倾斜相机间相对关系姿态误差,本文提出了一种基于联合平差的检校方法。实现了航空倾斜摄影系统多相机间相对位置关系的误差检校,该方法不需要在下视影像和倾斜影像间匹配同名点。对于倾斜立体像对,通过图7和图10检校前后投影对比图,可以看出C、D相机方向的立体像对所属标记区域的投影在相机检校前无论左、右影像均不能投影至正确位置,经过检校后,C、D相机的点云可以准确投影至正确位置。通过表1和表2连接点的精度分析,可以得到检校前左右影像的投影误差值均在20个像素以上。采用本文方法进行检校后,左、右影像的投影误差均方差均小于0.5个像素,高程方向的均方误差为0.040 m左右。通过对比实验可以看出本文方法检校后,倾斜影像的外方位元素相对初始外方位元素精度得到很大提高,可以满足后续密集匹配以及纹理映射等工作的需求。
[1]王卿,郭增长,李豪,等.多角度倾斜摄影系统三维量测方法研究[J].测绘工程,2014,23(3):10-14.
[2]曲林,冯洋,支玲美,等.基于无人机倾斜摄影数据的实景三维建模研究[J].测绘与空间地理信息,2015,38(3):38-39.
[3]刘力荣,左建章,岳贵杰.SWD-5倾斜摄影建筑物纹理自动映射方法[J]. 测绘科学,2015,40(8):68-71.
[4]SIMMONS G,KARBO N. Aerial imagery from different angles[J].Professional Surveyor,2007,27(5): 18-23.
[5]RUPNIK E,NEX F,TOSCHI I,et al. Aerial multi-camera systems: Accuracy and block triangulation issues[J].ISPRS Journal of Photogrammetry and Remote Sensing,2015,101: 233-246.
[6]QTAISHAT K,SMITH M,PARK D. Direct georeferencing and UltraCamD misalignment calibration [C].ASPRS conference,Portland,USA,2008.
[7]姚娜,林宗坚,任超锋,等.顾及同步差的POS系统视准轴误差检校[J].武汉大学学报(信息科学版),2013,38(2): 181-18.
[8]袁修孝. POS 辅助光束法区域网平差[J].测绘学报,2008,37(3):343-348.
[9]钟良,马洪超,管海燕,等.利用安置角检校进行机载LiDAR点云数据与同步影像快速配准[J].武汉大学学报(信息科学版),2011,36(9): 1035-1038.
[10] 刘凤英,王冬,陈天恩,等.三维相机检校场标志点图像坐标提取方法[J].测绘工程,2015,24(7):48-52.
[11] LOWE D.Distinctive Image Features from Scale-invariant Keypoints [J].International Journal of Computer Vision,2004,60(2): 91-110.
[12] FISCHLER M,BOLLES R. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography [J].Communications of the ACM,1981,24(6): 381-395.
[13] 范东明.非线性最小二乘参数平差迭代算法[J].测绘学院学报,2001,18(3): 173-175.
[14] HAN S P. A globally convergent method for nonlinear programming[J].Journal of optimization theory and applications,1977,22(3): 297-309.
[15] HAN S P. Superlinearly convergent variable metric algorithms for general nonlinear programming problems[J].Mathematical Programming,1976,11(1): 263-282.
[16] WU B,ZHANG Y,ZHU Q.A Triangulation-Based Hierarchical Image Matching Method for Wide-Baseline Images [J].Photogrammetric Engineering & Remote Sensing,2011,77(7): 695-708.
[责任编辑:刘文霞]
Calibration method for installation attitude error between multi-cameras of airborne oblique photogrammetry system
FENG Yanfei, ZHANG Yunsheng, DU Shouji
(School of Geosciences and Info-Physics, Central South University, Changsha 410083,China)
Aiming at the attitude parameter error between multi-cameras of airborne oblique photogrammetry system, this paper proposes a method based on combined adjustment which uses the dense matching point cloud from nadir image for a constraint. This method is based on collinear equation, by integrating tie points, virtual observation from point cloud data derived from nadir image based on dense matching as an elevation constraint, and using the principle of least-squares adjustment with SQPM algorithm to solve the corrections of exterior orientation elements of oblique images. Then high-precision attitude parameter can be obtained.To ensure the reliability of the tie point, and the effectiveness of virtual observations, the point cloud derived from dense matching is used for constraining tie point matching and distribution optimization processing. Images from SWDC-5 oblique photography system are used for experiments. By projecting the point cloud data from nadir image and using dense matching to stereo oblique images wih the initial attitude parameter, there are about 22 pixels error in image space. After calibration based on the proposed method, the error is reduced to 0.29 pixels.
airborne oblique photogrammetry system; calibration; combined adjustment; SQPM algorithm
10.19349/j.cnki.issn1006-7949.2016.08.011
2015-04-11;
2015-08-31
冯雁飞(1989-),男,硕士研究生.
P231
A
1006-7949(2016)08-0045-08

