基于自适应Kalman滤波的边坡变形预测研究
胡自全,何秀凤
(1.西安市地下铁道有限责任公司,陕西 西安 710018;2.河海大学 卫星及空间信息应用研究所,江苏 南京 210098)
基于自适应Kalman滤波的边坡变形预测研究
胡自全1,2,何秀凤2
(1.西安市地下铁道有限责任公司,陕西 西安 710018;2.河海大学 卫星及空间信息应用研究所,江苏 南京 210098)
摘要:研究Kalman滤波和自适应Kalman滤波算法,结合边坡监测点的运动模型将其应用于边坡变形监测动态数据变形预测。利用小湾水电站二号山梁高边坡GPS监测数据进行实验研究。结果表明,自适应Kalman滤波在边坡三维形变预测及变形速率估算方面有很好的预测结果。
关键词:自适应Kalman滤波;变形监测;边坡;变形预测
使用Kalman滤波处理动态数据能够有效消除随机干扰噪声,取得接近真实的数据信息[1]。变形监测过程中,变形体均处于一个动态变化的过程[2-3],获得的监测数据,除包含变形过程中各监测试块变形体的变化状态外,还有各种干扰噪声。当采用Kalman滤波实时处理变形监测所获得实时数据,能够得到较好的效果[4-5]。近年来,工程界在多方面开展了关于Kalman滤波的研究工作,特别是在变形监测领域得到了广泛的应用[6-7]。
Kalman滤波方程在应用过程中要求函数模型和随机模型可靠,估计方法合理。但是,变形监测过程中变形体一般都是无规则运动,因此,构造精确的函数模型非常困难。Kalman滤波应用中一般是基于验前统计信息来获取随机模型先验信息,在难以精确表征当前物理显示和观测显示新的情况下,任何统计信息都有可能失真[8-10]。在Kalman滤波过程中,由估计过程自适应地调整、更新先验信息的算法即是自适应Kalman滤波[1]。
1Kalman滤波方程
Kalman滤波算法的系统状态方程和观测方程的离散化形式为[3]
(1)
并有
(2)
式中:Xk为k时刻系统的状态向量,Φk,k-1为k-1到k时刻的系统状态转移矩阵,Γk,k-1为k-1到k时刻系统状态噪声输入矩阵,Ζk为k时刻系统观测向量,Hk为k时刻系统的观测矩阵,Wk-1为k-1时刻动态噪声向量,Vk为k时刻系统观测噪声[3]。根据最小方差线性递推估计,可以推算得到标准Kalman滤波的递推公式[3]。
状态预测向量为
(3)
其协方差阵
(4)
新息向量及其协方差矩阵
(5)
(6)
Kalman滤波增益矩阵
(7)
状态估计向量的协方差阵
(8)
状态估计向量
(9)
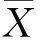
2自适应Kalman滤波算法
自适应滤波解的极值形式为[1]
(10)
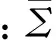
(11)
(12)
求得
(13)
(14)
代入观测方程
(15)
代入式(14)得
(16)
令新的增益矩阵为
(17)
状态参数自适应滤波解
(18)
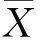
(19)
可写成
(20)
3监测点运动模型
3.1状态方程
例如边坡监测点i在时刻t的位移量为si(t),变形速率为vi(t),把变形速率作为一阶Markov随机过程,可得方程[4]
(21)
其中τ为相关时间常数。设监测点三维形变量及其速率状态向量为
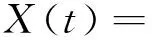
(22)
并有
(23)
式(21)可写为
(24)
将式(24)离散化得
(25)
有
(26)
(27)
3.2观测方程
考虑边坡监测点i在t时刻的观测方程为[3]
(28)
设
(29)
观测方程离散化为
(30)
其中
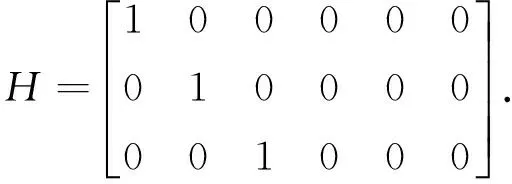
(31)
4试验研究与结果分析
小湾水电站2#山梁GPS变形监测网由2个基准点和14个边坡监测点组成[11],见图1。基准点B1位于右岸、B2位于左岸;监测点TP-25、TP-22、TP-30、TP-36、TP-29A、TP-35联接在一台GPS多天线控制器上,TP-01、TP-04、TP-09、TP-14、TP-15、
TP-18、TP-29、TP-33接在另一台GPS多天线控制器[12-13]。2个基准点和14个边坡监测点使用4台NOVATEL GPS接收机和4套GPRS无线数据传输终端。该系统自2004-06建成运行,至今获得了大量的观测数据。
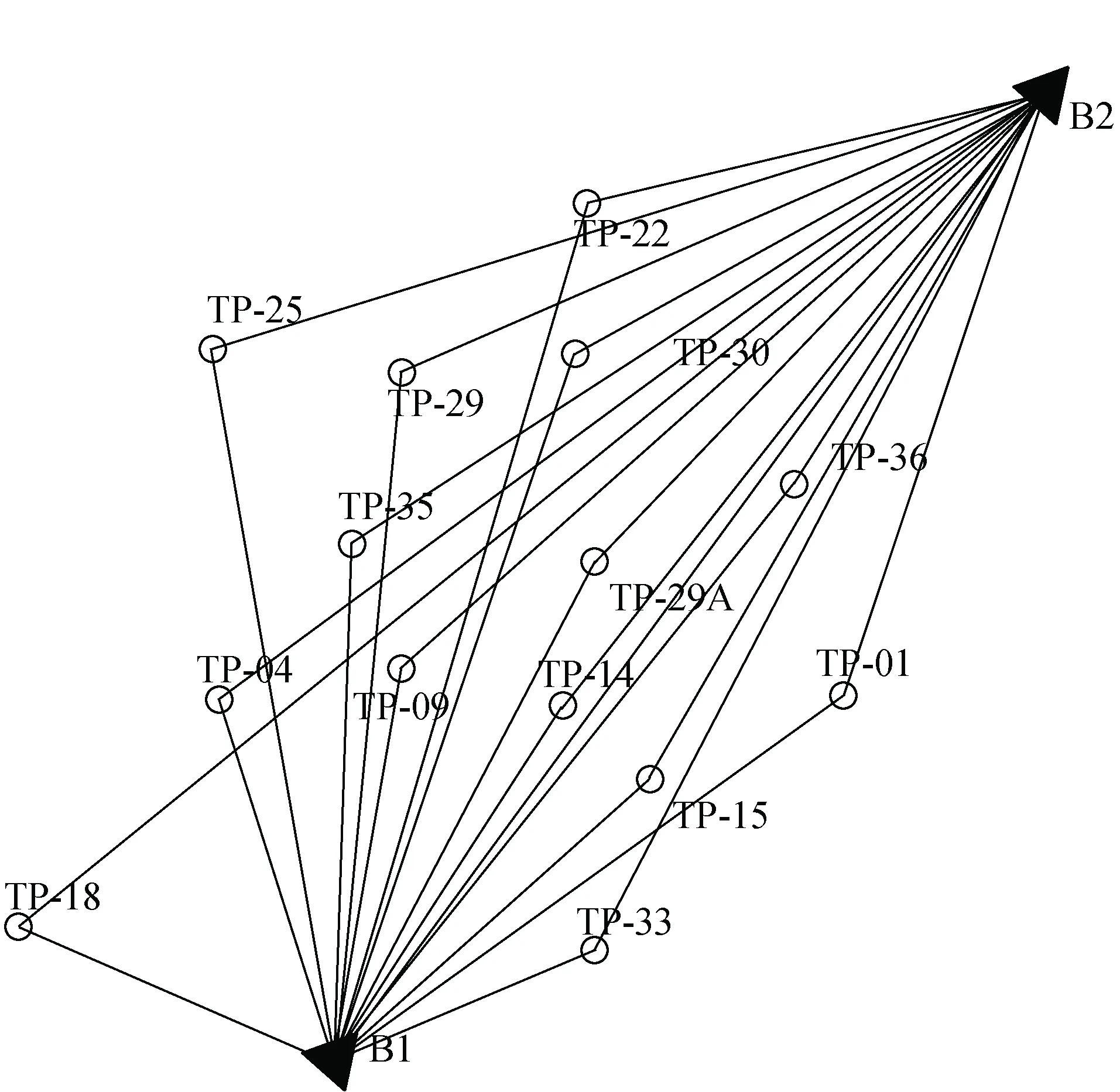
图1 小湾水电站二号山梁GPS监测网示意图
本文选取TP-29、TP-30、TP-35和TP-36 4个监测点,2004-06-15—2006-09-16共800 d 1600期的观测数据,部分数据见图2。
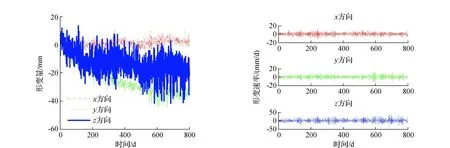
图2 TP-30点原始监测数据时间序列图
应用Kalman滤波及自适应Kalman滤波,建立监测点的运动模型的状态方程和观测方程,选取初始值,确定最优自适应因子,估计其形变量及形变速率,部分结果如图3、图4所示。并根据参数估值的均方误差(MSE)估计滤波的精度[1,13-15],结果见表1、表2。
从图3、图4可以看到,Kalman滤波和自适应Kalman滤波三维形变滤波曲线经过短暂的抖动后逐渐趋于平稳,最后接近某一稳定值。大部分数据在经过15 d即30组数据的情况下就达到了稳定,表明模型收敛速率快,趋于平稳。其中,自适应Kalman滤波的收敛速率快于Kalman滤波,滤波曲线较为平滑,且自适应Kalman滤波的三维形变速率滤波曲线的收敛速度和稳定性显然优于Kalman滤波。
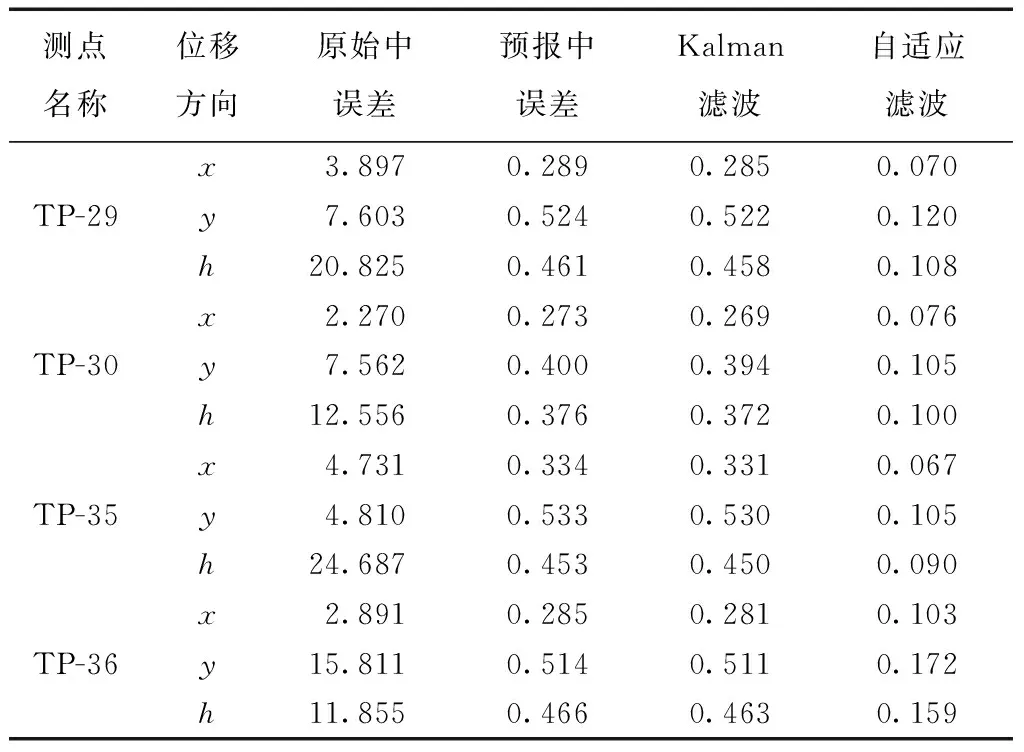
表1 监测点滤波前后变形量中误差 mm
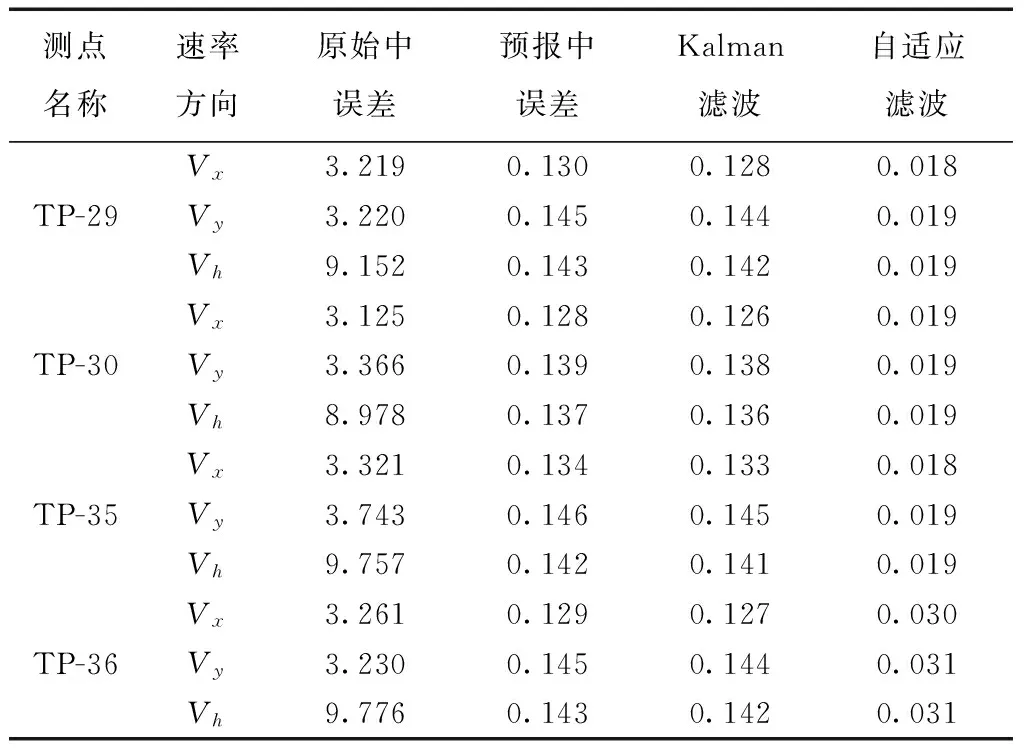
表2 监测点滤波前后变形速率中误差 mm/d
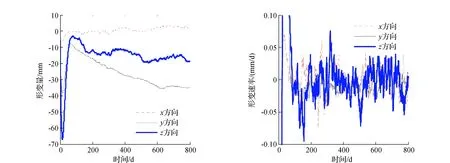
图3 TP-30点Kalman滤波结果
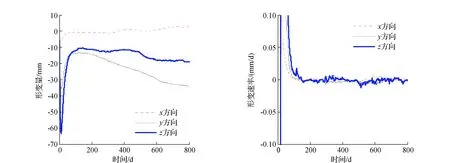
图4 TP-30点自适应Kalman滤波结果
由表1、表2知,相对于原始值的中误差,预报值和Kalman滤波值的中误差在三维位移方向和速度方向上都有明显提高。自适应Kalman滤波较Kalman滤波精度更高,尤其在三维速度方向上的精度。也反映出了与图形直观分析一致的特性,即自适应Kalman滤波方法处理变形监测的动态数据的精度和稳定性优于Kalman滤波方法。
5结束语
采用合理的理论方法对边坡变形时序数据进行建模,并预测监测点的形变量及形变速率,是变形监测的重要目的之一。在动态的变形监测系统中自适Kalman滤波在控制状态方程异常信息随状态参数估值和均方误差影响方面均有较好的效果。利用小湾水电站二号山梁高边坡4个GPS监测点监测数据进行的实验研究表明,自适应Kalman滤波较标准Kalman滤波在边坡三维形变预测及变形速度估算上都有更高的预测精度和稳定性。
参考文献:
[1]杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.
[2]刘祖强 张正禄 邹启新 等.工程变形监测分析预报的理论与实践[M].北京:中国水利水电出版社,2008.
[3]华锡生,田林亚.安全监测原理与方法[M].南京:河海大学出版社,2007.
[4]何秀凤.变形监测新方法及其应用[M].北京:科学出版社,2007.
[5]贾东振.基于GPS多天线技术的滑坡监测系统设计与实现[D].南京:河海大学,2006.
[6]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2003.
[7]尹晖.时空变形分析与预报的理论和方法[M].北京:测绘出版社,2002.
[8]杨元喜.动态自适应滤波解的性质[J].测绘学报,2003,32(3):198-192.
[9]杨元喜.论动态自适应滤波[J].测绘学报,2001,30(4):293-298.
[10] 王冰,隋立芬,吴江飞,等.基于状态矩阵卡尔曼滤波的姿态估计算法研究[J].测绘工程,2013,22(5):21-24.
[11] 何秀凤 华锡生.GPS一机多天线变形监测系统[J].水电自动化与大坝监测,2002,26(3):34-37.
[12] 贾东振,何秀凤,桑文刚.小湾水电站高边坡GPS变形监测数据库管理信息系统开发[J].水电自动化与大坝监测,2005,29(6):40-42.
[13] 胡自全.基于GNSS的边坡变形监测与预报方法研究[D].南京:河海大学,2010.
[14] 许阿裴,归庆明,韩松辉.Kalman滤波模型中三种残差的比较[J].黑龙江工程学院学报(自然科学版),2008,22(2):22-25.
[15] 袁曼飞,靳洁,刘钰.基于Sage-Husa自适应kalman滤波的磁悬浮陀螺转子信号处理[J].测绘与空间地理信息,2015,38(4):59-60.
[责任编辑:刘文霞]
DOI:10.19349/j.cnki.issn1006-7949.2016.08.008
收稿日期:2015-04-29
基金项目:国家自然科学基金资助项目(50579013);国家自然科学基金委员会和二滩水电开发有限责任公司雅砻江水电开发联合研究基金资助项目(50579110)
作者简介:胡自全(1983-),男,工程师.
中图分类号:P228;TU196
文献标识码:A
文章编号:1006-7949(2016)08-0033-05
Prediction of slope deformation based on adaptive Kalman filtering
HU Ziquan1,2,HE Xiufeng2
(1.Xi’an Metro Co.,Ltd,Xi’an 710018,China;2.Institute of Satellite Navigation and Spatial Information System,Hohai University,Nanjing 210098,China)
Abstract:It presents the Kalman filter and the adaptive Kalman filtering algorithm.Combined with the establishment of monitoring movement of the slope model,this algorithm is applied to the slope monitoring data dynamic deformation prediction.The experiment uses GPS monitoring data on the 2nd ridge slope of Xiaowan Hydropower Station,which shows that the adaptive Kalman filtering in the slope three-dimensional deformation prediction and rate estimation has a good predictive result.
Key words:adaptive Kalman filtering;deformation monitoring;slope;deformation prediction

