基于K-Medoid聚类算法的GPS坐标转换研究

王　伟，黄　腾，葛　文，曹晓桢，张浩然

(1.河海大学 地球科学与工程学院，江苏 南京 210098；2.国家基础地理信息中心，北京 100830)



基于K-Medoid聚类算法的GPS坐标转换研究

王伟1，黄腾1，葛文1，曹晓桢1，张浩然2

(1.河海大学 地球科学与工程学院，江苏 南京 210098；2.国家基础地理信息中心，北京 100830)

摘要：对GPS网约束平差时，GPS控制网的精度与坐标系统转换控制点的位置选择有关。通过实验分析得出，整个网的检核点与相应的转换控制点总距离越远，坐标转换后网的精度越低。在此基础上，提出使用K-Medoid聚类算法，通过计算机程序自动寻找用于计算坐标系统转换参数的最佳控制点，并将文中方法运用于某大桥GPS控制网的控制点选取，通过工程实例验证了基于K-Medoid聚类方法的GPS坐标系统转换的可行性。

关键词：K-Medoid算法；GPS网；基线解算；网平差；坐标转换；精度评价

GPS定位技术[1]的平面精度能达到1～2 mm，甚至能达到亚毫米级。实际工程中，需要对GPS接收机直接获取的WGS-84坐标进行转换，得到GPS网点的工程独立坐标。目前,常用转换方法的主要技术路线如下：在测区选取2个或2个以上的转换控制点，联测高等级的点，利用四参数模型[2]或七个参数模型[3-4]，计算得到GPS网的WGS-84坐标系与地方独立坐标系之间的转换参数，再对GPS网进行约束平差，获取GPS控制网的工程独立坐标。已有研究表明[5]，在基线质量良好的情况下，若转换控制点选取不合理，会导致整个网扭曲变形，改变网点误差的分布规律，从而使相应的方差与协方差模型产生变化，降低GPS网精度。行业相关规范中对转换控制点的选择并没有明确规定，实际工程一般根据经验来选择，但是并不能保证选取的转换控制点是合适的。本文针对上述问题，将机器学习中的K-Medoid算法(K中心点算法)引入到控制点选取中，优化控制点选取方案，从而获得最佳控制点，提高GPS网的精度。

1K-Medoid聚类算法

聚类是将数据对象分组为多个类或簇，划分原则是在同一个簇中的对象之间具有较高的相似度，而不同簇中的对象差别较大，每一个类可以通过一些特征来描述。K-Medoid聚类算法[6]选用簇中位置最中心的对象作为代表对象，试图对n个对象给出k个划分，代表对象称为中心点，其他对象被称为非代表对象。在K-Medoid聚类算法中，可以把过程分为以下2个步骤：

1)建立。寻找k个中心点作为初始的类中心点。

2)交换。对于所有的可能的对象进行分析，找到交换后可使得非代表对象到该对象的欧氏距离和最小的对象，代替原中心点。

2GPS网精度评价

2.1Chi-SquareTest

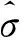
(1)

对母体方差σ2进行假设检验的方法，称为χ2检验法。

2.2Tau-test

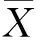
(2)

检验正态母体的数学期望。GPS基线解算中，Tau检验一般用来检验参与平差的基线是否存在粗差[7]。

2.3QA检验

三维无约束平差后计算的基线向量中误差应满足预设值。QA检验[7]通过，表示基线向量中误差满足期望值。

3工程概况

临海高等级公路灌河大桥总体呈东西走向，横跨灌河，测区范围东经119°45′～119°50′，北纬34°23′～34°25′，北部位于连云港市境内，南部位于盐城市境内，线路总长约7.5 km。测区内地势平

坦，海拔2 m左右，因灌河南北两部分测区之间通行极为不便，布设GPS施工期控制网，等级GPS测量主要技术要求见表1。主桥、GH-1标引桥、GH-2标引桥GPS控制网测量点位缩略图分别见图1～图3。

图1　主桥GPS测量点位略图

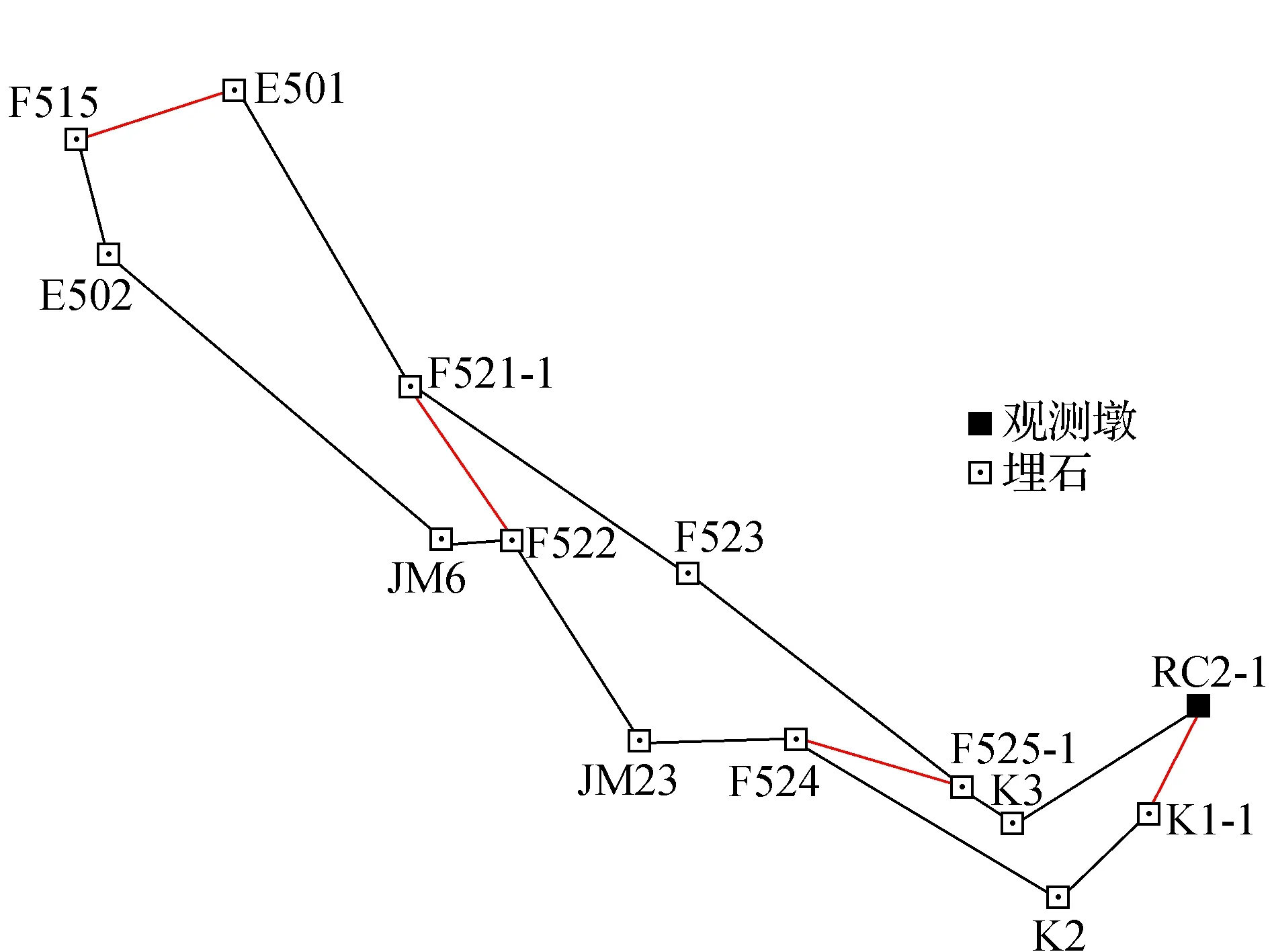
图2　GH-1标引桥GPS测量点位略图

图3　GH-2标引桥GPS测量点位略图

等级卫星高度角/(°)同时观测有效卫星数/个平均重复设站数/(次/点)时段长度/min数据采集间隔/sGDOP值三等≥15≥4≥2≥905～15≤6

特大型桥梁的施工期一般在2年以上，施工周期长，控制点使用频繁。由于该桥梁工程施工区域通常地质条件较差，周围作业机械较多，控制点不稳定因素较多，易受到破坏，因此，需定期对点位的稳定性进行检核，并进行修正。若坐标转换控制点不稳定，则需重新选取转换控制点。

4基于K-Medoid聚类算法的坐标转换的精度模拟分析

为了解决网的精度及点位误差大小与转换控制点位置的关系问题，利用计算机进行数据模拟，采用控制变量的方法，只研究控制点的偶然误差对网精度的影响。模拟过程如下：

2)灌河大桥三等GPS网要求最弱点点位中误差≤±5 cm，在测量平差学科中，有如下极限误差理论：

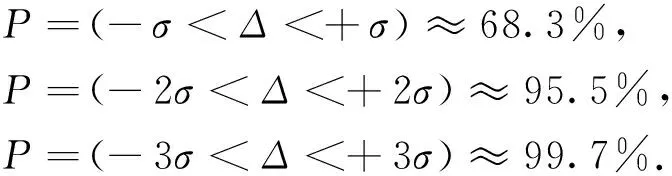
(3)

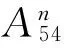
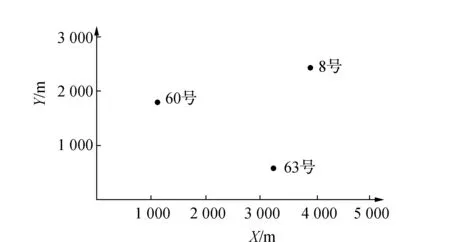
图4　K-Medoid算法选取的转换控制点

4)按如下公式计算2个不同转换模型下的点位误差。得到点位精度对比图(见图6)，选取最大点位误差、最小点位误差、小于两倍中误差比例、大于两倍中误差比例作为评价指标，得到精度分析表(见表2)。

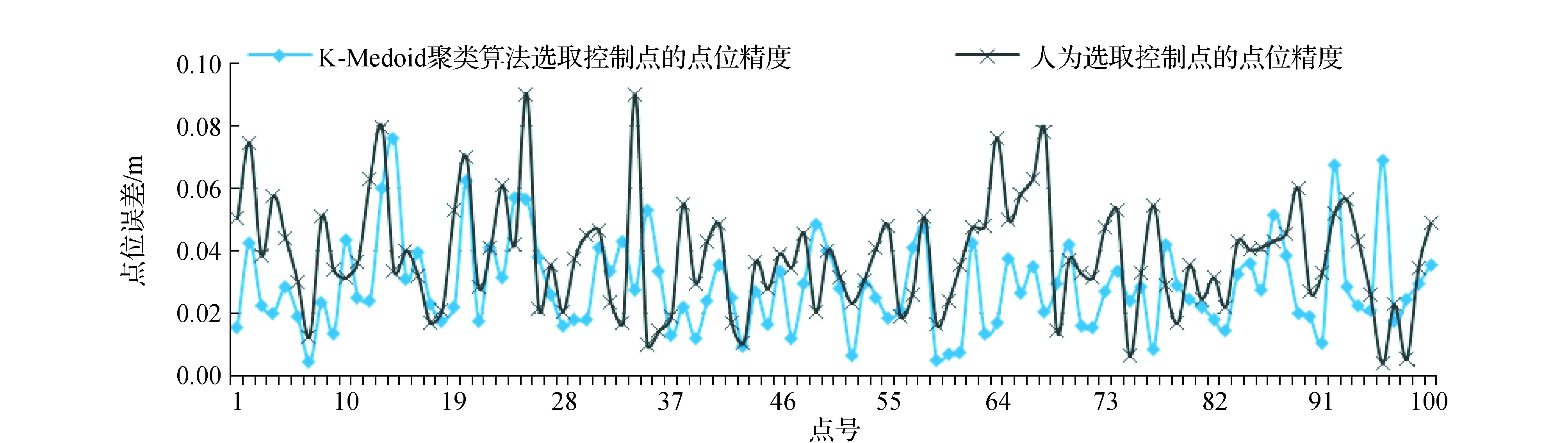
图6　K-Medoid聚类算法与人为选取转换控制点点位误差比较

(4)

(5)

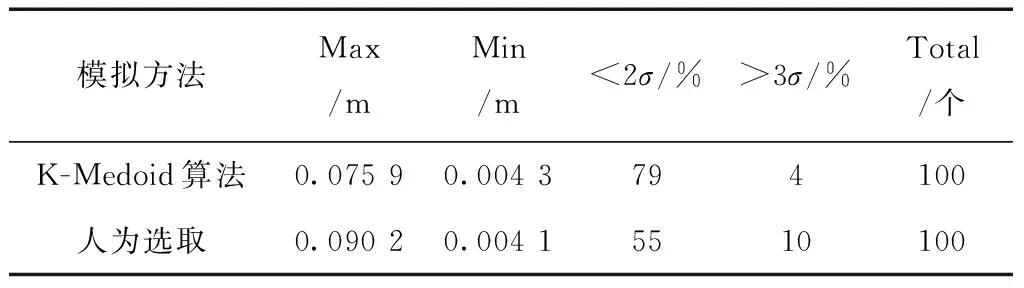
表2　K-Medoid聚类算法与人为选取转换控制点精度分析

5工程实例分析

5.1GPS数据预处理

5.1.1数据文件预处理

本实验利用Ashtech solution软件对基线进行基线处理。由于不同数据处理软件有各自特定的数据格式，在数据处理前，需将GPS数据观测文件转换为RINEX数据格式。

5.1.2基线解算及质量检核

基线解算过程主要分以下3步：①解算整周未知参数和基线向量浮动解；②将整周未知数固定成整数；③将整周未知数作为已知值，求解基线向量固定解。

基线解算完毕后对基线解算结果进行质量检核[8]。内容包括同步环检核、异步环检核以及复测基线检核等，保证基线质量合格后，对GPS网进行平差。

5.1.3三维无约束平差

进行网格坐标系(北京54高斯投影后的平面坐标系)下的无约束平差，获取测区内各GPS控制点的北京54平面坐标。将生成的各控制点的北京54平面坐标以电子表格的形式存档，作为K-Medoid聚类算法聚类的原始数据。

5.2基于K-Medoid聚类算法的转换控制点选取

K-Medoid聚类方法的实现借助于MATLAB，按照K-Medoid聚类的思想编写程序。为了体现实验方法的科学性，将整个处理过程分为以下2步：

1)三维无约束平差后，分别对各控制点的北京54平面坐标的三维空间坐标和二维平面坐标的聚类，共分成3类。为防止出现局部最优解，选取不同的初始点重复试验。试验结果显示，当重复聚类次数超过20次后，得到的聚类结果唯一；无论选用三维坐标还是二维坐标进行聚类，最终选出的聚类中心一致，依次是JM13、JM2-1、F524，其具体位置如图7所示，聚类之后各个点的分类情况见图8。

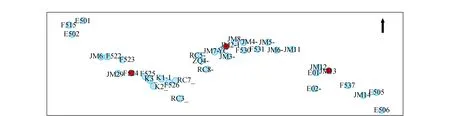
图7　转换控制点点位分布图

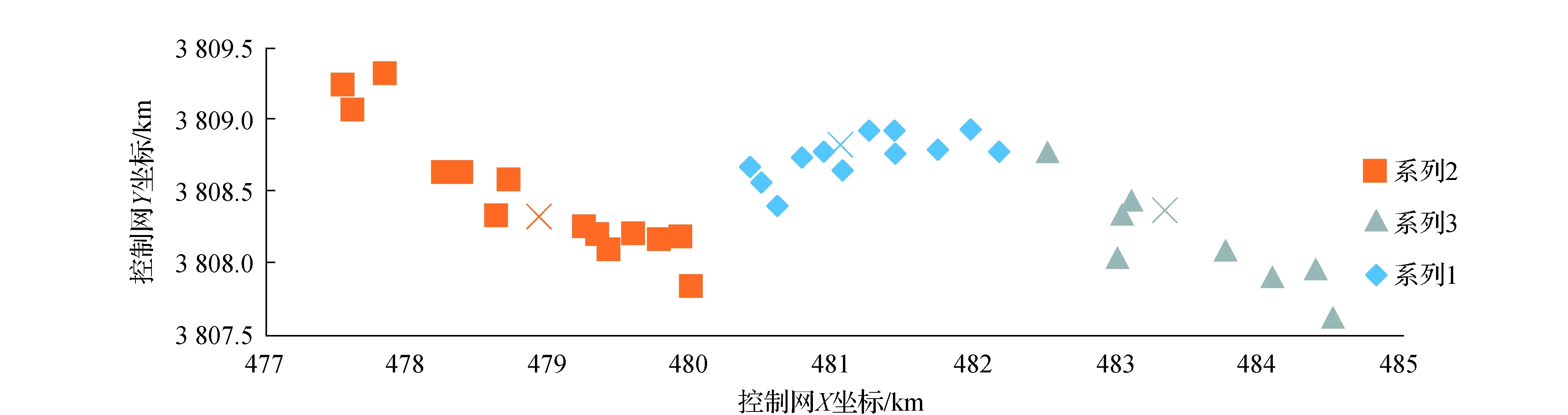
图8　控制点分类结果，以相同图例表示同一类控制点

2)选取聚类得到的JM13、JM2-1、F524这3个点作为转换控制点，对控制网进行约束平差。在网平差结束后，应对网平差结果进行检验，网平差的检验主要通过改正数、中误差以及相应的数理统计检验结果等项来评价。利用Ashtech solution软件的“Ashtech Network Adjustment Package”网精度评价模块提供的各项精度指标，对网精度进行评判，三维约束平差后的各项网精度指标如表3所示。

表3　三维约束平差网精度指标

平差结果显示，利用K-Medoid聚类算法找出转换控制点并进行在当地坐标系下约束平差后，该工程实例GPS网精度符合各项限差要求，网的各项精度指标得到保证。

6结论

利用K-Medoid聚类算法，通过计算机程序实现GPS网最佳转换控制点选取的方法，能够保证坐标转换控制点均匀分布于控制网，对测区域形成整体控制，从而能保证GPS网精度。灌河大桥施工期控制网的实例验证了基于K-Medoid聚类方法的GPS坐标系统转换的可行性，可为其他工程实例提供参考。

参考文献：

[1]徐绍全.GPS测量原理及应用[M].武汉：武汉大学出版社，1998.

[2]韦铖，马文双，李明君.工程测量中平面坐标转换软件设计及应用[J].测绘工程，2013，22(4):76-79.

[3]田桂娥，宋利杰，尹利文，等.地方坐标系与CGCS2000坐标系转换方法的研究[J].测绘工程，2014，23(8):66-69.

[4]王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学，2007，27 (2):43-46.

[5]陶叶青，杨娟，赵强.控制点因素对GPS坐标系统转换精度的影响[J].北京测绘，2012(1)：5-7.

[6]KAUFLNAN L，ROUSSEAUW P J.Finding Groups in Data：An Introduction to Cluster Analysis[J].Journal of the American Statistical Association，1990.

[7]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社，2003.

[8]王瑞.GPS基线精度分析及控制网的方差分量估计研究[D].南京：河海大学，2005.

[责任编辑：刘文霞]

DOI:10.19349/j.cnki.issn1006-7949.2016.08.006

收稿日期：2015-04-27

作者简介：王伟(1991-)，男，硕士研究生.

中图分类号：P228.4

文献标识码：A

文章编号：1006-7949(2016)08-0024-05

A study of GPS coordinate transformation theory based on the algorithm of K-Medoid

WANG Wei1，HUANG Teng1，GE Wen1，CAO Xiaozhen1，ZHANG Haoran2

(1.School of Earth Science and Engineering，Hohai University，Nanjing 210098，China；2.National Fundamental Geographic Information Center，Beijing 100830，China)

Abstract：When conducting the constraint adjustment of GPS network，the accuracy of GPS control network is related to the choice in the location of the conversion control points of the coordinate system.Through the experimental analysis，the paper reaches a conclusion：the longer the total distance of the checking points and conversion control points are，the lower precision of the network is.Based on this conclusion，the algorithm of K-Medoid is used to find the best conversion control points and applying this to the GPS network of a certain bridge can prove the feasibility of this method.

Key words：algorithm of K-Medoid；GPS network；baseline processing；network adjustment；transformation of coordinate；evaluation of precision