K-GM(1，1)模型在岩体变形监测中的应用

马符讯，席瑞杰，徐　南

(1.武汉大学 卫星导航定位技术研究中心，湖北 武汉 430079；2.武汉大学 测绘学院，湖北 武汉 430079；3.清华大学 地球系统科学研究中心，北京 100084)



K-GM(1，1)模型在岩体变形监测中的应用

马符讯1，席瑞杰2，徐南3

(1.武汉大学 卫星导航定位技术研究中心，湖北 武汉 430079；2.武汉大学 测绘学院，湖北 武汉 430079；3.清华大学 地球系统科学研究中心，北京 100084)

摘要：传统GM(1，1)模型存在着长期预测效果差、模型精度不高等问题，卡尔曼滤波能够排除建模过程中随机干扰因素，滤波值能够反映更真实的数据情况。为了能更好地提高变形监测的预测精度，基于传统GM(1，1)模型和卡尔曼滤波，提出K-GM(1，1)模型，利用该模型对岩体变形监测数据进行建模预测，并与传统GM(1，1)模型预测结果进行对比分析，结果表明，K-GM(1，1)模型具有较高的预测精度，可作为变形监测的一种新方法。

关键词：卡尔曼滤波；GM(1，1)模型；预测；变形监测

1基于卡尔曼滤波的灰色模型

1.1传统GM(1，1)模型

设某系统原始观测序列：X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)}，X(0)一次累加生成X(1)序列：X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)}，其中

(1)

当X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)}是时间t的连续可微函数并满足一阶微分方程：

(2)

式中：参数a为发展系数，表征系统的发展走势；参数b为灰色作用量，表征数据变化的关系。

则GM(1，1)的时间响应函数

(3)

最后通过累减得到预测值：

(4)

1.2K-GM(1,1)模型

卡尔曼滤波是一种通过对被提取信号有关的观测量的算法估计得出所需信号的滤波方法。离散系统的卡尔曼滤波的动态方程和量测方程

(5)

(6)

式中：xk,ωk-1分别为k时刻的状态变量和动态噪声;φk,k-1为k-1时刻到k时刻的状态转移矩阵；zk,Hk,vk分别为k时刻的观测向量、量测方程系数矩阵和量测噪声。

离散线性系统的状态估计问题本质上就是根据观测向量z1,z2,…,zk的数学模型，求得第tj时刻的状态向量xk最优估值的问题，一般分为3种情况：

卡尔曼滤波过程的求解结果为

(7)

(8)

其中

Jk=

变形监测工程中，通常影响因素较多且相对复

杂，变形时间序列中不仅存在白噪声，可能还存在着有色噪声，从而产生建模误差。本文构建的K-GM(1,1)模型，设定卡尔曼滤波过程的状态参数为监测点的位移量及其位移速度，设定动态噪声为监测点的位移加速度，故卡尔曼滤波动态方程为

式中：xk,vk,ak分别为监测点的位移量，位移速度和加速度;ωk-1为动态噪声;tk-1表示时间。K-GM(1,1)模型处理流程如图1所示。

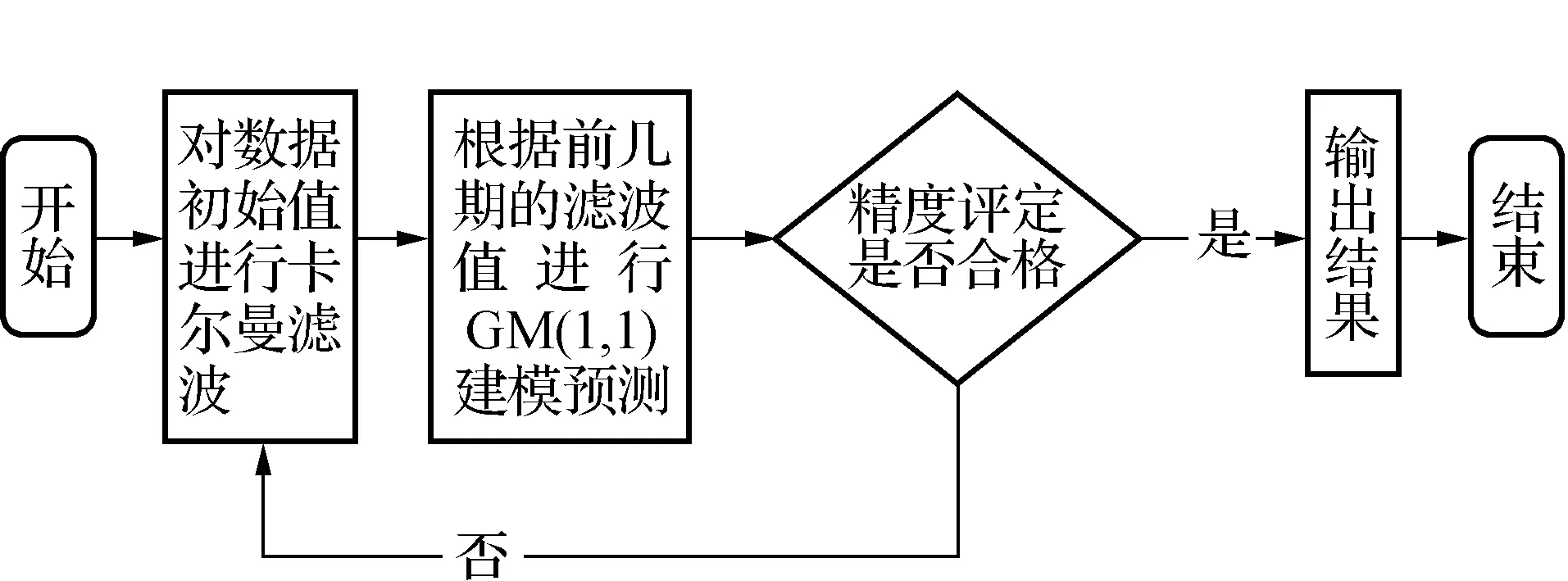
图1　K-GM(1,1)模型处理流程

2工程实例

为保证隧道建成后洞口岩体的安全性，于2014年开始对其进行健康监测，监测周期为1个月，同时为验证K-GM(1，1)模型的有效性，本文以某隧道出口洞顶岩体监测点2014年前11期的沉降监测值为例,如表1 所示，其中前5期的实测值为原始序列，试验过程为首先利用卡尔曼滤波对其建模数据进行处理，剔除随机扰动误差的影响，再运用灰色理论对滤波值进行建模，并预测后6期的变形发展趋势，最后计算实测值与预测结果的残差，验证模型的可靠性。

表1　某岩体监测点2014年前11期的沉降监测值

2.1传统GM(1,1)模型预测

首先选取原始观测序列的前5期进行建模，再利用传统的GM(1,1)模型对后6期数据进行预测，通过计算求得原始观测值和预测值的残差，对预测结果进行评估。传统GM(1,1)模型预测结果如表2所示。

由表2可以看出，传统的GM(1,1)模型预测精度总体良好，但存在随预测时间增加，预测精度下降的情况，传统的GM(1,1)模型在长期预测方面模型的预测精度不能得到很好的保证，不能反映岩体最真实的变形规律和变形趋势。

表2　传统GM(1,1)模型预测

2.2K-GM(1,1)模型预测

表3　原始序列的卡尔曼滤波结果

由表3可以看出，滤波值由第二期开始收敛，协方差基本也稳定在0.001以内，同时其变化趋势为越来越小，逐渐趋近于0。在此基础上，本文再利用传统GM(1,1)模型对前5期的卡尔曼滤波值进行建模预测，后6期的预测结果如表4所示。

表4　K-GM(1,1)模型预测　mm

图2　K-GM(1,1)模型与传统GM(1,1)模型预测值比较

图2所示为传统GM(1,1)模型与K-GM(1,1)模型预测值对比结果，从图2中可以看出，K-GM(1,1)模型预测精度总体良好，优于传统GM(1,1)模型的预测精度，但随着预测时间的增加，该模型也呈现了预测精度下降的趋势，这与GM(1,1)的模型特点有关，卡尔曼滤波的作用只是剔除建模数据中的干扰因素，并不能排除预测过程中的误差源。K-GM(1,1)模型的预测值相比传统GM(1,1)模型更接近真实的变形值。因此，经过改进K-GM(1,1)模型可以更好的反映岩体的变形规律和变形趋势。

3结论

本文利用卡尔曼滤波和传统GM(1,1)模型构造出K-GM(1,1)模型，利用该模型对岩体变形数据进行分析预测，并与传统GM(1,1)模型的预测结果进行对比分析，结论：K-GM(1，1)模型的预测精度优于传统的GM(1，1)模型，但依然存在着长期预测精度低的问题，这与传统GM(1,1)的模型原理有关，今后可引入自适应动态调节因子，建立动态GM(1,1)模型解决该问题。总之，本文提出的K-GM(1,1)模型程序实现简单，预测精度高，具有更好的预测效果，故K-GM(1，1)模型在岩体变形预测中具有较高的应用价值。

参考文献：

[1]邓聚龙.灰色系统基本方法[M].湖北：华中工学院出版社,1987.

[2]李日云,王利,张双成.灰色预测模型在高层建筑物沉降预测中的应用研究[J].地球科学与环境学报,2005,27(1)：23-26.

[3]甘月云,陈星,付军,等.基于灰色预测GM(1，1)模型的城镇生活需水量预测[J].水电能源科学，2012(9):40-42.

[4]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2010.

[5]喜文飞,史正涛.基于卡尔曼滤波的动态灰色理论模型研究[J].测绘工程,2014,23(3):24-27.

[6]吴彦,张铎强,徐南.反向灰色模型的初值优化在道路沉降中应用[J].测绘工程,2014,23(12)：60-62.

[7]INCE C D,SAHIN M.Real-time deformation monitoring with GPS and Kalman Filter[J].Earth Planets and Space,2000,52(10)：837-840.

[8]王琦,孙华,李伟华，等.卡尔曼滤波在变形监测数据处理中的应用[J].工程地球物理学报,2009,6(5):658-661.

[9]文鸿雁,周吕,韩亚坤，等.基于卡尔曼滤波的GM(1,1)模型在高铁隧道沉降变形分析中的应用[J].大地测量与地球动力学,2014,34(1):88-91.

[10] 任远军，李龙，石宁，等.改进的 GM(1，1) 模型在大坝变形预测中的应用[J].测绘工程，2015,24(6)：61-64.

[11] 姜刚,杨志强,张贵钢.卡尔曼滤波算法的灰色理论模型在变形监测中的应用[J].测绘科学,2011,36(4):19-21.

[责任编辑：李铭娜]

DOI:10.19349/j.cnki.issn1006-7949.2016.08.010

收稿日期：2015-05-07；修回日期：2015-06-25

基金项目：国家自然科学基金资助项目(41374033)

作者简介：马符讯(1992-)，男，硕士研究生.

中图分类号：F291.1

文献标识码：A

文章编号：1006-7949(2016)08-0042-03

Application of K-GM(1，1)model to the deformation monitoring of rocks

MA Fuxun1，XI Ruijie2，XU Nan3

(1.Research Center of GNSS,Wuhan University,Wuhan 430079,China；2.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China；3.Center of Earth System Sciences，Tsinghua University,Beijing 100084,China)

Abstract：There are some problems in the tradition GM(1,1) forecast models such as the bad effect in the long term prediction and the low accuracy and so on.Therefore,Kalman filter method has the advantage of eliminating random interference factors in the process of modeling,and the filtered data can reflect the real situation of the project.In order to improve the prediction accuracy of deformation monitoring,this paper proposes to use the K-GM (1,1) model,based on the GM (1,1) model and Kalman filter,and to analyze the rock mass deformation monitoring data.The results indicate that comparing with the GM(1,1) model,the K-GM(1,1) model can achieve a higher prediction accuracy,which can be used as a new method for deformation monitoring.

Key words：Kalman filtering;GM(1，1)；forecast；deformation monitoring