阻尼特性对超高层混合结构的振动响应分析

杨全胜刘 唤(上海联创建筑设计有限公司郑州分公司 河南 郑州 450000 商丘工学院 土木工程学院 河南 商丘 476000）

阻尼特性对超高层混合结构的振动响应分析

杨全胜1刘 唤2
(1上海联创建筑设计有限公司郑州分公司 河南 郑州 450000 2商丘工学院 土木工程学院 河南 商丘 476000）

混合结构体系由于自身的复杂性和特殊性，到目前为止结构的等效阻尼比尚未有较为科学、有效、普遍认可的取值方法或者计算方法。针对超高层混合结构，应用Etabs有限元软件对其进行动力分析，在构建阻尼矩阵时，通过采用黄本才教授的复阻尼计算方法所得的各阶振型阻尼比以及分别采取其他各种阻尼比值作为不同的计算工况，以黄本才教授的复阻尼计算方法所得的各阶振型阻尼比为准，对比分析出阻尼特性对超高层混合结构的动力响应影响，结果表明对同一超高层混合结构，即使阻尼比相差约1%时，也会引起结构体系振动响应相对误差20%左右的变化，相差约2%时，更是达到了40%的变化。

混合结构、超高层、等效阻尼比、动力响应、相对误差

0.引言

混合结构体系由于能够综合利用钢结构以及钢筋混凝土结构两者的优点，因此在超高层工程中得到越来越广泛的应用。然而这一类结构体系由于自身的复杂性和特殊性，结构的阻尼比尚未有较为科学、有效、普遍认可的取值方法或者计算方法。目前在超高层混合结构工程实际应用中，其阻尼比主要通过实测结果来获取。当然也有大量的工程通过较为简便的方法来确定，如按高规取折算阻尼比或者根据 Rayleigh阻尼模型确定等，显然不同的计算方法所得到的阻尼比值也不一样。众所周知，阻尼是影响结构动力响应最为重要的因素之一，其正确与否将直接关系到抗震分析结果的可靠性。本章应用Etabs有限元软件建立深圳某超高层建筑的计算分析模型，

以黄本才教授的复阻尼计算方法为准，分别采取其它不同的阻尼比值进行结构的动力响应分析，进而对比分析出阻尼特性对超高层混合结构的动力响应影响，为今后科学计算混合结构的等效阻尼比提供科学的参考。

1 工程背景

深圳某投资大厦位于深圳市南山区高新区填海六区01-11地块，占地面积5159.01平方米，容积率：15.64，底层平面布置图分别见图1所示。该大厦为一栋地下三层、地上四十四层的超高层建筑，总建筑高度186米。其总建筑面积为93043.75平方米：其中计容积率面积：80700.52平方米（商业用房面积：4750.00平方米，食堂面积：3250.00平方米，工业研发用房面积：70363.04平方米，骑楼：468.71平方米，避难区：1868.77平方米），地下停车位：600个。

图1 底层平面布置图Fig.1 The analysis model of ANSYS

该建筑采用框筒结构，周边采用X型斜网支撑结构。抗震设防烈度为7°，0.1g，场地特征周期Tg=0.45，周期折减系数为0.9，振型组合采用CQC法，方向组合采用SRSS法。

2 计算分析

2.1 有限元模型及振型信息

图2 Etabs计算模型Fig.2 The analysis model of ANSYS

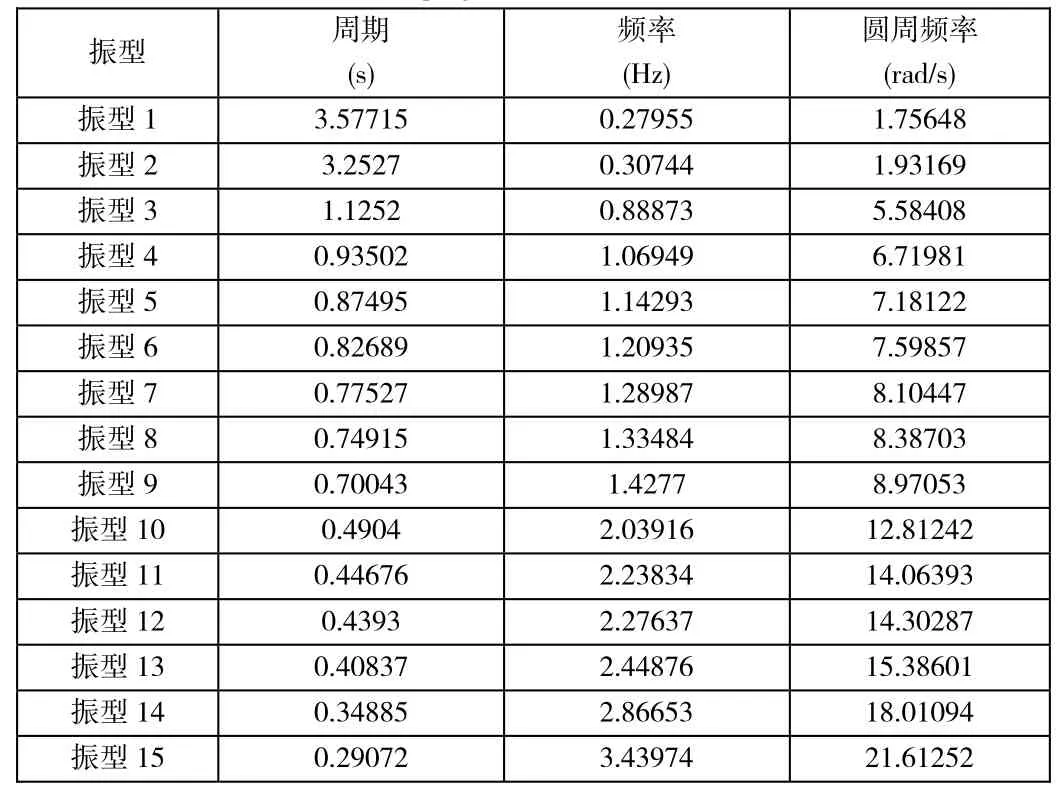
表1 超高层混合结构的振型信息Tab.1 each order modal damping ratio calculated

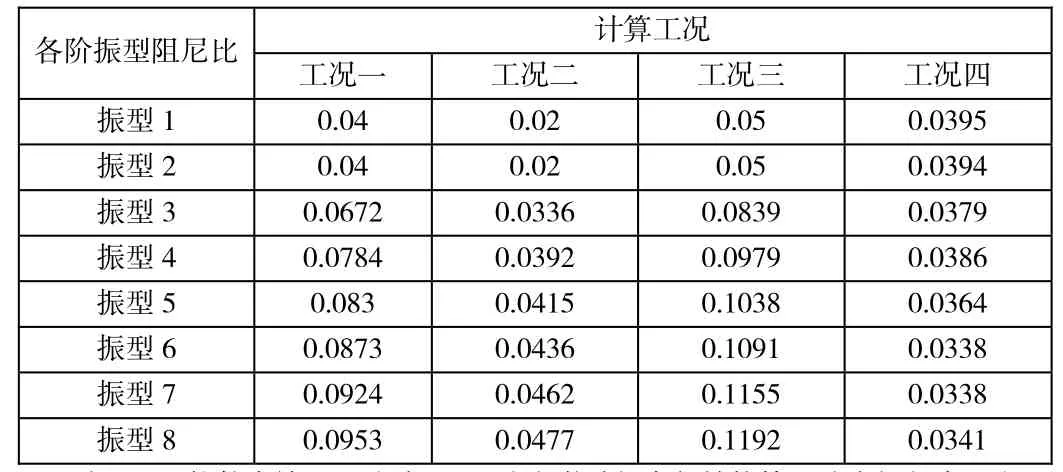
表2 各计算工况的各阶振型阻尼比Tab.2 each order modal damping ratio calculated

应用Etabs有限元软件建立的有限元模型如下所示：论来确定结构的阻尼作为不同的计算工况。其中工况一、工况二、工况三分别假定结构的前两阶振型阻尼比为0.04、0.02、0.05，根据文献[5] Rayleigh阻尼的计算方法分别确定结构体系的振型阻尼比，工况四根据黄本才教授[13]的基于复阻尼理论的阻尼比计算方法来确定结构的阻尼比，各计算工况具体如表2。

在Etabs软件中输入正弦波，通过改变激励频率与结构第一阶自振频率1之比β来观察采用不同的阻尼比对计算该混合结构的动力响应的差别，这里β分别取为0.8、0.9、1.0、1.1、1.2、1.3。

2.3 结构动力响应误差分析

这里取结构混合结构顶部和底部的动力响应峰值来分析，并以第4种计算工况为准，分别计算另外三种工况的阻尼模型所引起的相对误差，其计算公式为

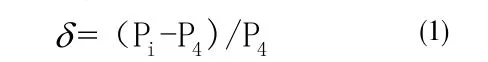
其中， Pi 为第i种计算工况对应的响应峰值，i=1，2，3； 容积效率[%]容积效率与压力的关系工况对应的响应峰值。

2.3.1 结构顶层动力响应误差

对于结构的顶部，由于假定楼板在平面内的刚度为无限大，这里取计算模型中的1624点的加速度和位移来分析，具体如图3、图4所示。

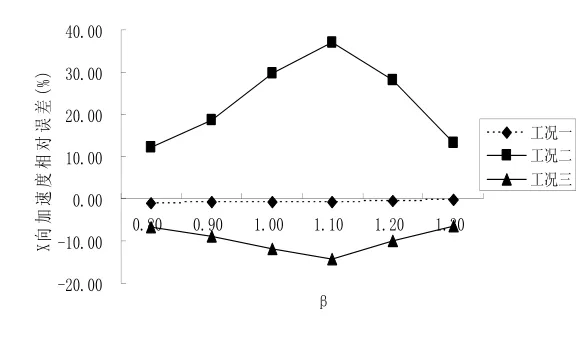
图3 X向加速度相对误差比较Fig.3 The analysis model of ANSYS

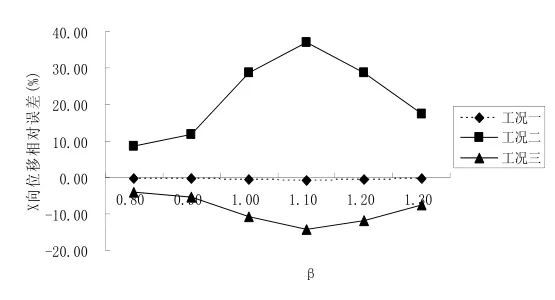
图4 X向位移相对误差比较Fig.4 The analysis model of ANSYS

2.3.2 结构底层动力响应误差

图5 X向基底抗剪相对误差比较

Fig.5 The analysis model of ANSYS

图6 Y向基底抗剪相对误差比较

Fig.6 The analysis model of ANSYS

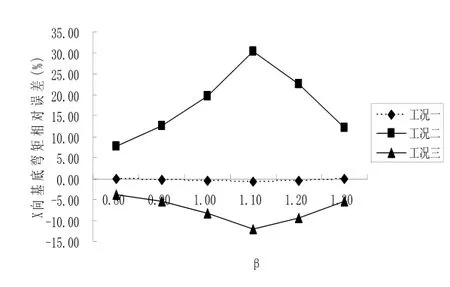
图7 X向基底弯矩相对误差比较Fig.7 The analysis model of ANSYS

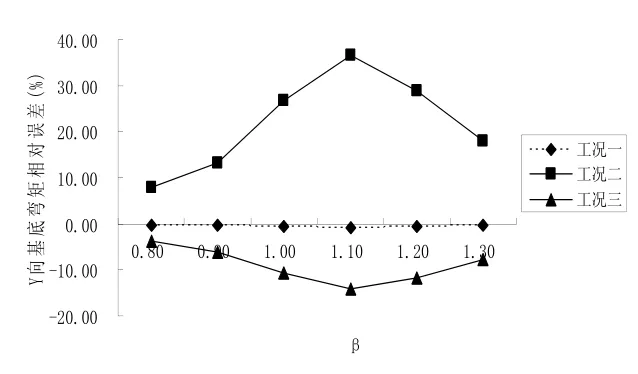
图8 Y向基底弯矩相对误差比较Fig.8 The analysis model of ANSYS

2.3.3 对比分析

从以上的关系图中可以看出：

(1) 工况二与工况四输入的阻尼比值仅相差 2%，但工况二计算的振动响应相对误差较大，峰值接近40%，而工况三与工况四输入的阻尼比值仅相差1%，工况三计算的振动响应相对误差的峰值也接近20%，均已超过计算误差所允许的范围，因此对同一混合结构，阻尼比极小的差异将会引起结构体系振动响应较大的变化。

(2) 工况一与工况四相比所计算输入的前两阶阻尼比均在 4%左右，两者仅相差约 0.5%，高阶振型阻尼比相差较大，然而所得的振动响应误差也均在 1%范围内，满足结构计算误差在5%范围内的要求，表明该混合结构前两阶振型的阻尼比约为4%，而且前两阶振型的阻尼比对于整体结构的耗能起主要作用。

(3) 当β约为1.1时，三种计算工况的振动响应误差均达到峰值，表明此时较为接近结构的共振频率，因此由共振法[14]同样可以求出混合结构的阻尼比。

3 结论

本章应用Etabs有限元软件对某一超高层建筑进行动力分析，在构建阻尼矩阵时，通过采用黄本才教授的复阻尼计算方法所得的各阶振型阻尼比以及分别采取其他各种阻尼比值作为不同的计算工况，以黄本才教授的复阻尼计算方法所得的各阶振型阻尼比为准，对比分析出阻尼特性对超高层混合结构的动力响应影响，为今后科学计算混合结构的等效阻尼比提供科学的参考。主要结论如下：

(1) 对同一超高层混合结构，阻尼比极小的差异将会引起结构体系振动响应较大的变化，即使阻尼比相差约1%时，也会引起结构体系振动响应20%的变化，相差2%时，更是达到了40%的变化。

(2) 对该超高层混合结构阻尼比取为4%时，振动响应误差均在1%范围内，基本满足结构设计的要求。

(3) 当激励频率与结构第一阶自振频率之比约为1.1时，激励频率接近结构的共振频率，振动响应误差达到峰值，随着激励频率远离共振频率，结构体系的响应误差也越来越小。

References:

[1]李国强，周向明，丁翔.高层建筑钢-混凝土混合结构模型模拟地震台试验研究[J].建筑结构学报，2001，22(2)：2-7.

[2]周国伟，张志强等.混合结构时程分析中的阻尼比计算研究[J].振动与冲击，2012，31(16)：117-127.

[3]黄方林，何旭辉，陈政清等.识别结构模态阻尼比的一种新方法[J].土木工程学报，2002，35(6)：20-23，31.

[4]林凡伟.轻木–混凝土混合结构振动台试验阻尼识别研究[D].上海：同济大学大学土木工程学院，2008：36-39.

[5]楼梦麟，康帅，殷琳.阻尼效应的振动台模型试验研究[J].同济大学学报（自然科学版），2012，40(3)：402-407.

[6]Clough R W,Penzien J. Dynamics of structures[M]. 3rd Edition. Berkeley，California，USA: Computers and Structures,Inc.,2003:52-61.

[7]Fritzen C P. Identification of Mass，Damping, and Stiffness Matrices of Mechanical Systems[J].Journal of Vibration and Acoustics,1986,108(1):9-16.

The Analysis of Super High-rise Mixed Structure on the Influences of Calculating Model Based on Different Damp

Uses finite element software Etabs to carry out dynamic analysis for the super high-rise hybrid structure, uses damping ratio of each order vibration mode got by calculation method of complex damping presented by professor Huang ben-cai, and adopts other types of damping ratio as different calculating conditions when constructs the damping matrix, compares the influence of damping on the dynamic response of super high-rise hybrid structure based on damping ratio calculated by the method presented by professor Huang ben-cai. The results show that structural vibration response changes about 20% even if the damping ratio differs about 1% , and the change reaches 40% when the damping ratio differs about 2% for the same super high-rise composite structure.

composite structure;super high-rise;equivalent damping ratio;dynamic response;relative error

TU311.3

B

1007-6344（2016）06-0298-02