主轴-球轴承系统的非线性频响研究

农胜隆，高尚晗

（1.广西科技大学鹿山学院，广西 柳州 545616；2.广西科技大学 机械工程学院，广西 柳州 545006）

因摩擦因数小、承载特性好，角接触球轴承广泛应用于高速机床电主轴系统。随着电主轴转速及精度要求的不断提高，需要对电主轴-角接触球轴承系统的非线性动态特性进行更深入的研究。

轴承参数对系统非线性动态特性的影响吸引了众多研究者的注意［1］。文献［2-3］将Hertz方程引入球轴承-转子整体系统模型中，研究轴承配置对主轴支承刚度的影响，发现轴承预紧力越大，支承刚度也越大，系统的固有频率也相应增大。文献［4-5］对球轴承支承刚性转子的稳定性问题进行了系统研究，通过相轨迹、庞卡莱映射及功率谱等描述了系统的周期、拟周期、混沌及分岔等振动响应特性，发现轴承内外圈的表面波纹度及钢球数量对转子系统的稳定性及动态响应均有较大影响，钢球表面波纹度的影响可忽略不计。游隙是引起系统非线性动态响应的关键因素，通常用于补偿主轴高速转动时出现的热膨胀。文献［6］对非线性轴承游隙影响下的Jeffcott转子系统进行研究，发现其振幅随轴承径向游隙增大而减小。

钢球与内外圈之间为点接触［5］，可采用非线性非光滑的Hertz接触力进行建模。因此，系统研究了Hertz接触力作用下，轴承负游隙对系统非线性振动响应的影响，为进一步提高主轴-球轴承系统的稳定性提供一定的理论基础。

1 Bernoulli-Euler梁模型及边界条件

电主轴结构如图1所示，当主轴高速旋转时，转子的柔性振动响应特征明显。可根据电主轴结构特点，将转子简化为连续梁模型，如图2所示，轴承1位于第1段转子末端的A点，轴承2位于第1段与第2段转子之间的B点。采用Bernoulli-Euler连续梁模型对高速电主轴转子-轴承的振动响应进行研究，角接触球轴承及转子的参数见文献［7］。

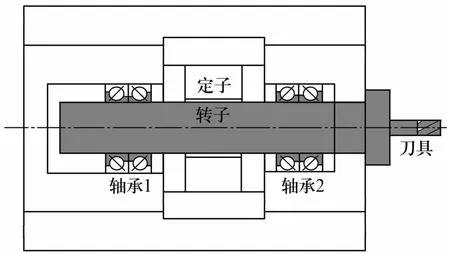
图1 电主轴结构示意图Fig.1 Structure diagram of motorized spindle

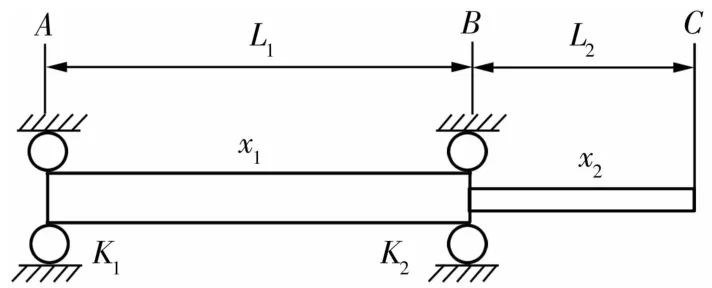
图2 主轴-球轴承简化模型Fig.2 Simplified model of spindle-ball bearing

为使系统的研究结果具有通用性，需要对系统振动响应偏微分方程组及其边界条件进行量纲一化，由此引入以下量纲一的量:为量纲一的转子轴向坐标;为量纲一的转子横向振幅；x为转子的轴向坐标；y为转子的横向振幅；e为转子不平衡量；L为转子长度；ω为转动频率；t为时间；ωs为计算频率；E为弹性模量；I为转子的横截转动惯量；ρ为转子密度；A为转子的横截面积；η为量纲一频率；δ为转子单位长度截面系数；r0为转子截面系数；为量纲一的径向游隙；Gr为径向游隙；λ为截面系数比；下标1，2分别表示图2所示简化模型的第1，2段转子；即

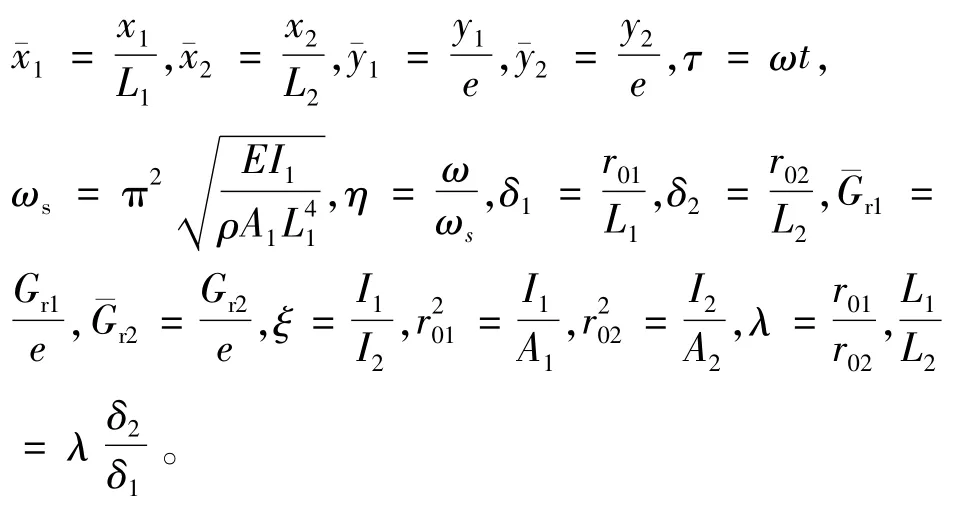
若不考虑剪切变形及转动惯量的影响，对于图2的二阶Bernoulli-Euler连续梁模型，其振动响应的偏微分方程组为

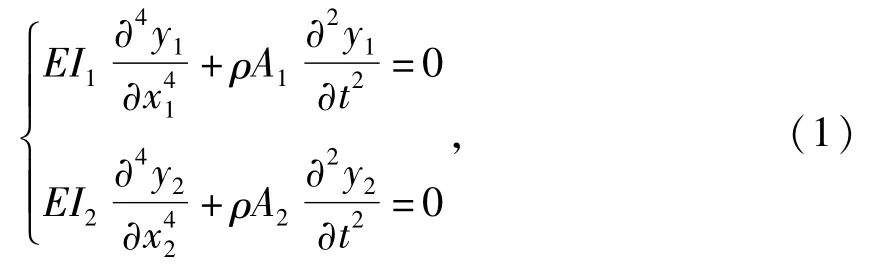
则量纲一的偏微分方程组为

根据Hertz弹性理论［4］，球轴承支承力为

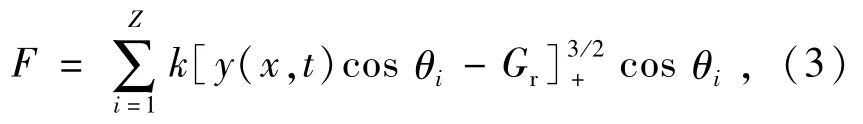
式中：k为钢球与内外圈的接触刚度；θi为第i个钢球的相位角；Z为钢球个数。由此可知，球轴承支承力具有非线性非连续特性，而该特性会引起电主轴-球轴承系统产生复杂的非线性响应。

（1）式描述连续梁所固有的振动特性。而整体转子-轴承系统的动态响应则需要引入边界条件来确定［8］，边界条件即为转子运动边界上方程的解应该满足的条件。由（3）式及文献［8］中连续梁的边界条件表达式可知，2阶连续转子在A点的边界条件为

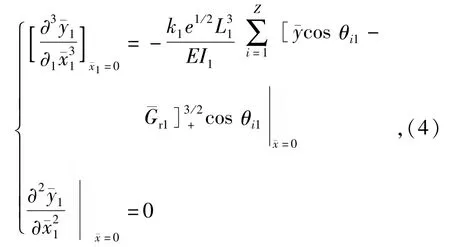
点B的边界条件为

式中：Fe为转子的不平衡力。

C点的边界条件为

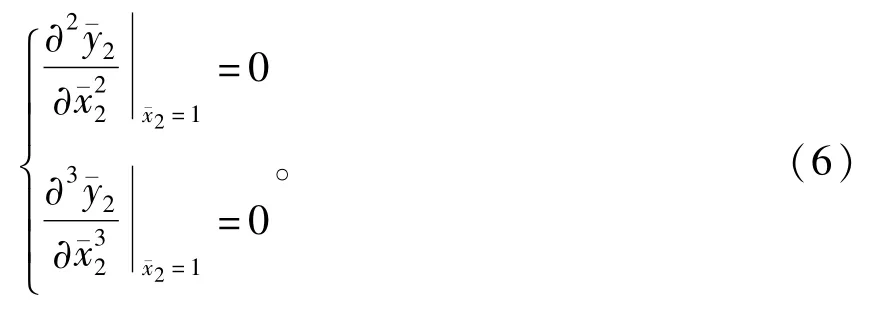
2 特征方程

引入

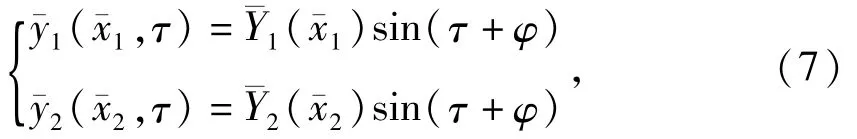
式中：φ为转子响应相位角。

将（7）式代入（6）式，消去sin（τ+φ），得

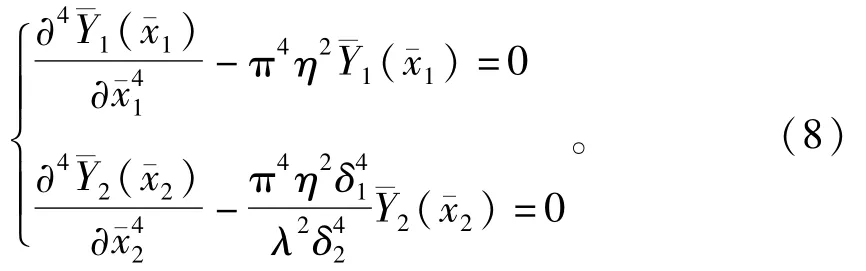
定义系数如下

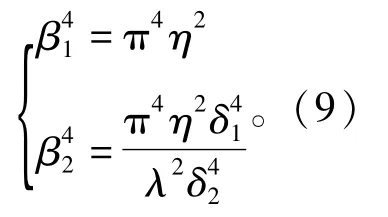
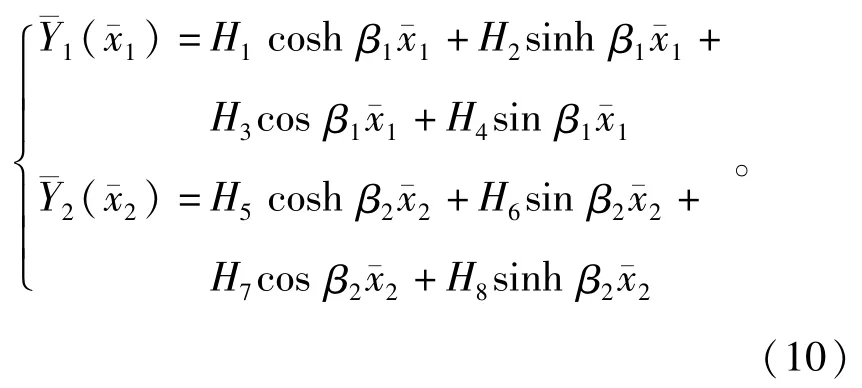
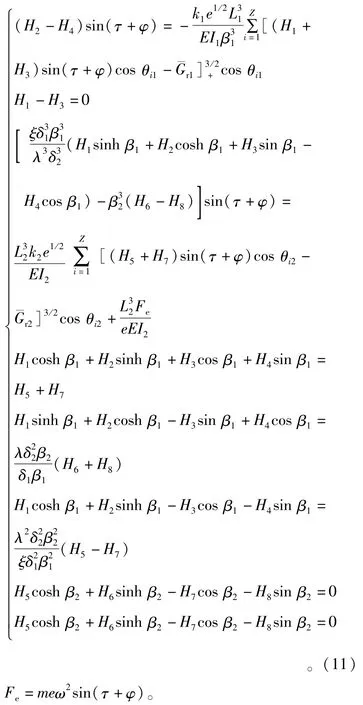
通过求解（11）式，可得到不同的频率η下的函数H1～H8，进而求得确切的系统方程模态函数，最终得到系统的频率响应曲线。

令

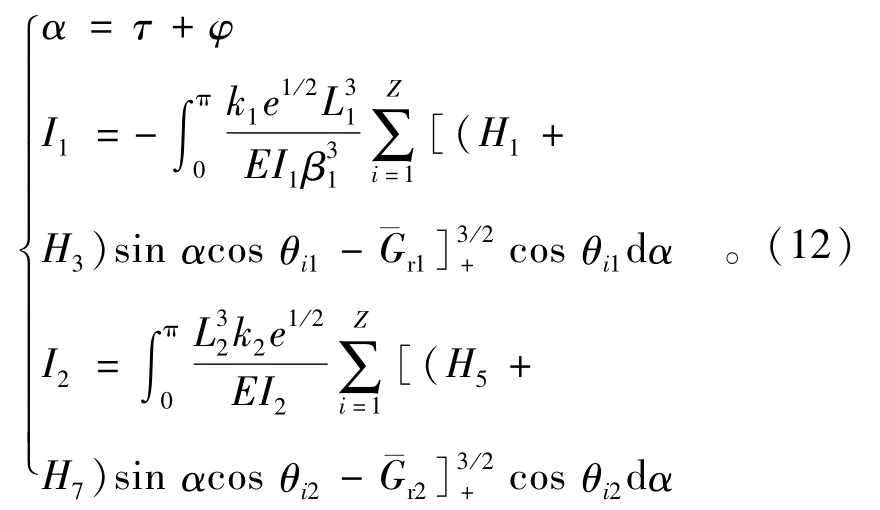
特征方程组（11）式可通过平均法求得，即在0～π范围内对α进行积分，得系统特征方程组为

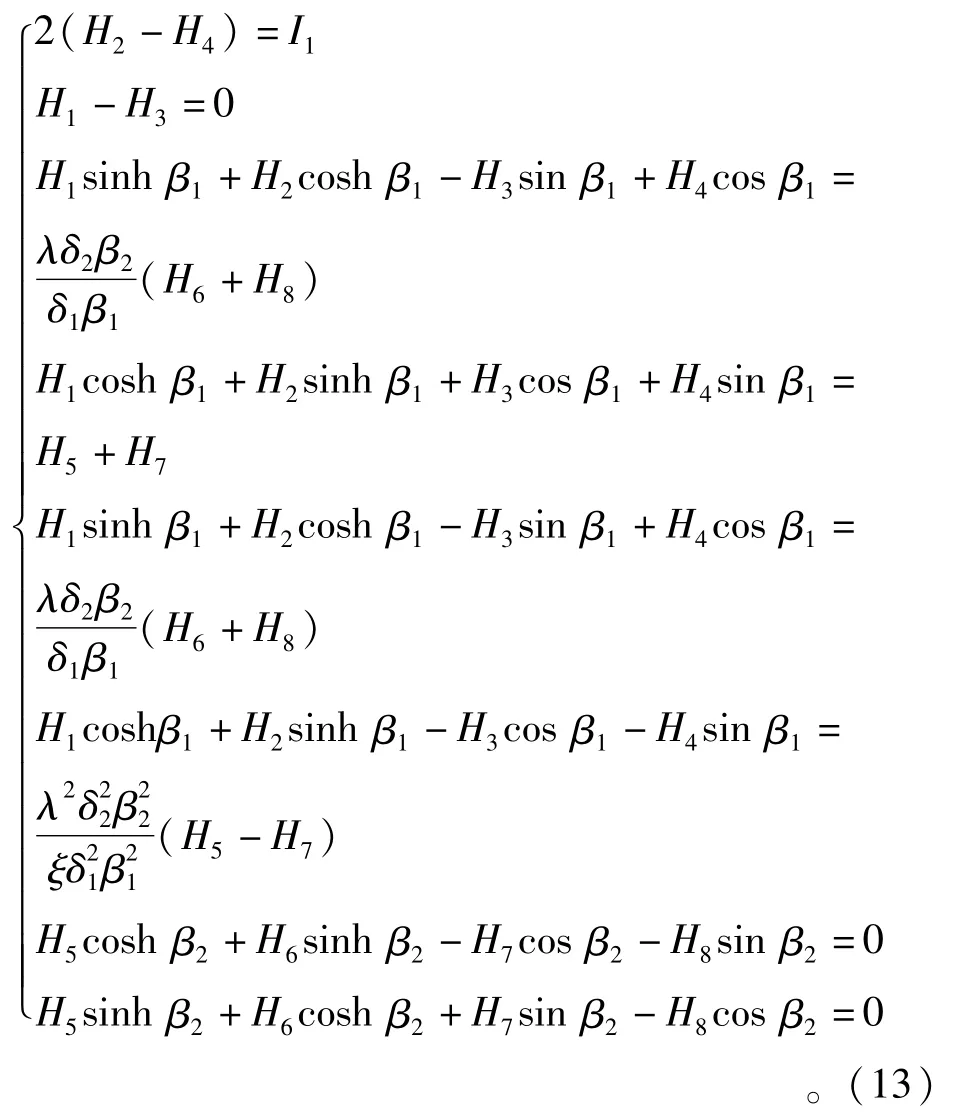
转子-轴承系统连续梁模型与有限元模型的频响曲线如图3所示。角接触球轴承的线性刚度表达式与文献［7］相同，且轴承预紧力Fa＝200 N。由图可知，连续梁模型与有限元模型固有频率的误差在1.2%以内，其误差在允许范围之内，说明文中所建立的连续梁模型是可靠的。有限元模型的固有频率比连续梁模型大，是由于连续梁模型的柔性大，其固有频率较小。

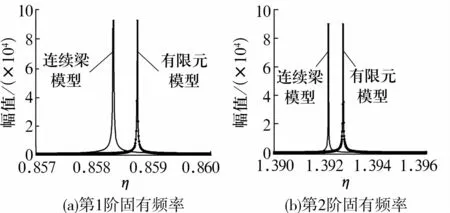
图3 连续梁模型与有限元模型频响曲线Fig.3 Frequency response curves of continuous beam model and finite element model

由于系统的边界条件具有非线性非连续特性，因此，转子-轴承系统的特征方程组（13）式是非线性非连续方程组，其系统频响曲线会表现出复杂的非线性振动响应特征。

3 计算结果

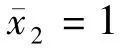
轴承1游隙固定在-5，轴承2游隙变化时，系统第1阶固有频率附近的频响曲线如图4所示。由图4a可知，当系统频率η较小，并离第1阶固有频率（M1点）较远，系统的振动响应稳定，1个η值对应1个振幅；当η接近第1阶固有频率时，系统频响曲线向右弯曲，在M2点处，1个η值对应3个幅值，系统响应明显呈现非线性。若减小轴承负游隙值，系统频响曲线如图4b所示，右弯曲之前有短暂左弯曲现象，但在其非线性响应区域，1个值仍对应3个幅值。继续减小轴承负游隙值（图4c），系统频响曲线的左弯曲幅度更大，出现了1个值对应5个幅值的非线性响应区域。由图4可知，轴承负游隙值减小，系统的第1阶固有频率会增大，非线性频响曲线右弯曲的幅度会降低。

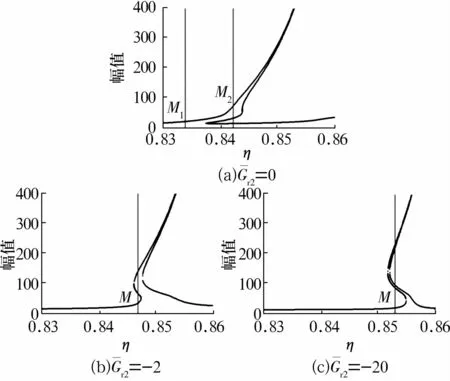
图4 轴承2游隙变化时，系统第1阶固有频率附近的频响曲线Fig.4 Frequency response curves near the first natural frequency of system with clearance variation of bearing 2

当轴承1与2的游隙都为0时，系统的频响曲线如图5所示，其频响曲线会出现交叉，但图3中未出现该现象。由此可知，频响曲线的交叉是由于球轴承的非连续支承特性引起的。若想避免交叉，则需减小轴承负游隙值，即削弱轴承非连续特性的影响。

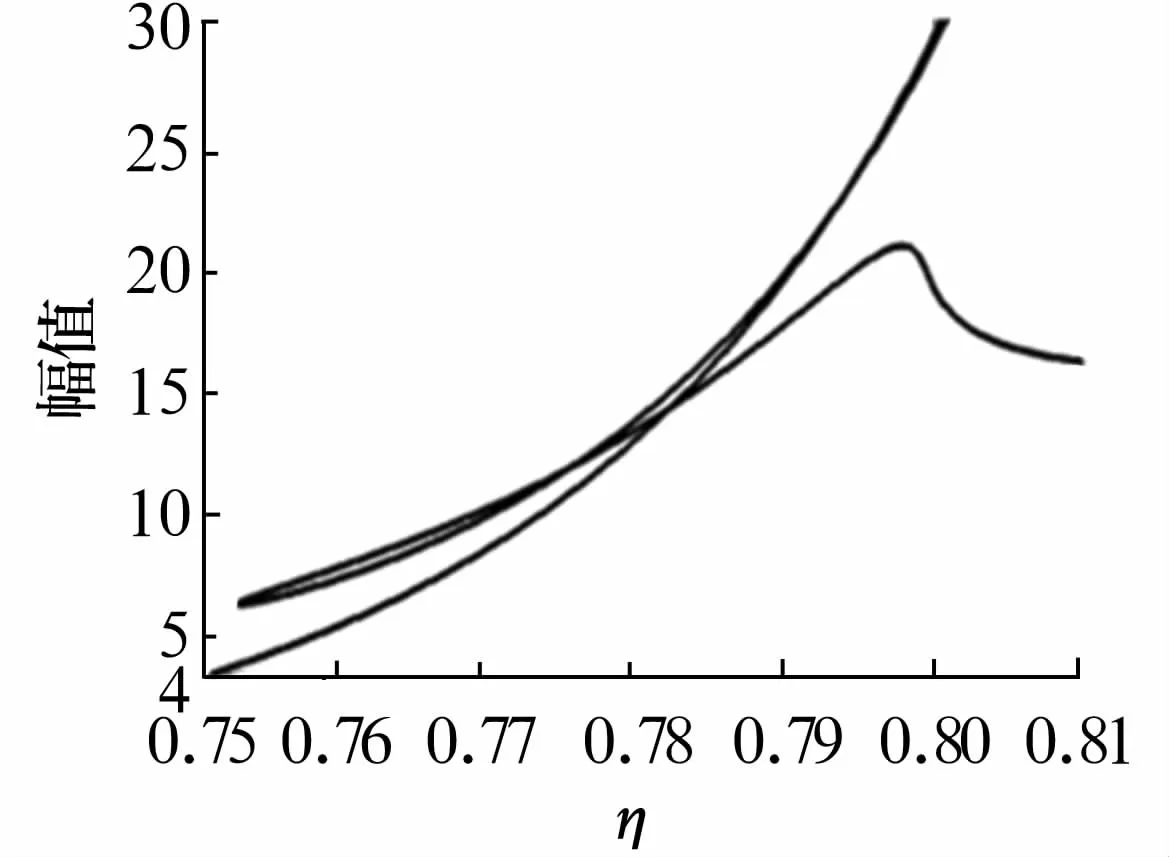
图5 ＝＝0时，系统的频响曲线Fig.5 Frequency response curves of system with＝＝0

轴承1游隙固定在-5，轴承2游隙变化时，第2阶固有频率附近的频响曲线如图6所示，该曲线同样表现出明显的硬刚度特性。与第1阶固有频率处的非线性频响曲线特性类似，当轴承负游隙值较大时，第2阶固有频率附近出现1个值对应3个幅值的非线性响应区域（图6a）；减小轴承负游隙值，会出现1个值对应5个幅值的非线性响应区域（图6b）。随轴承负游隙值减小，频响曲线的多值区域减小，其背骨线向右弯曲的程度也随之降低。

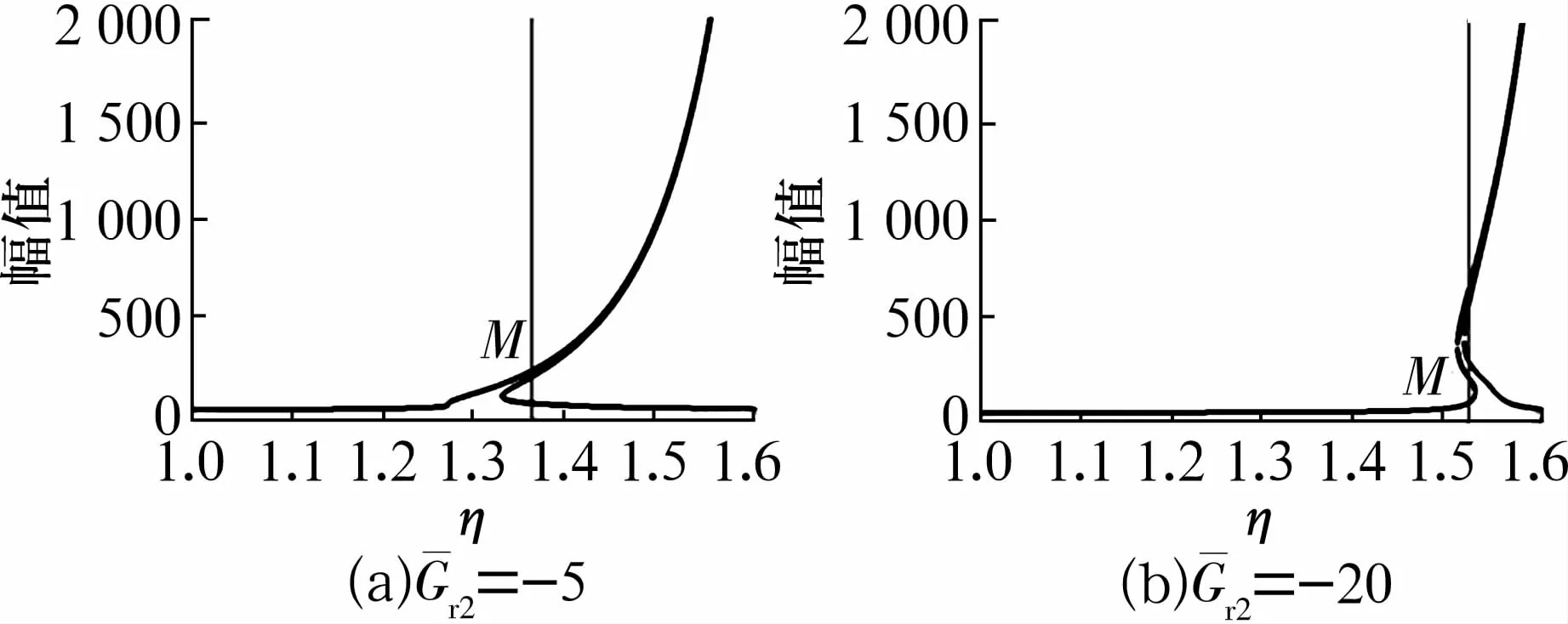
图6 轴承2游隙变化时，系统第2阶固有频率附近的频响曲线Fig.6 Frequency response curves near the second natural frequency of system with clearance variation of bearing 2

由以上计算结果可知，当轴承负游隙值较大时，轴承的非线性及非连续特性较为明显，背骨线向右弯曲的幅度较大，其响应的非稳定区域也较大；减小轴承负游隙值，钢球及套圈的接触区域增加，轴承的非线性及非连续特性相应减弱，背骨线向右弯曲的幅度减小，非稳定区域也同样减小。

4 结束语

由于轴承非线性非连续Hertz支承特性的影响，系统频响曲线呈现硬刚度特性。随着轴承负游隙值减小，系统的硬刚度特性相应减弱，故可通过减小轴承负游隙值来减小非线性响应区域。由于钢球与内外圈之间的非连续点接触，主轴系统的频响曲线中还会出现交叉现象。分析结果为角接触球轴承的设计分析提供了参考。