高精密球轴承保持架间隙的仿真分析

孙朝阳，马小梅，4，唐强，葛世东，4，刘良勇

（1.洛阳轴研科技股份有限公司，河南 洛阳 471039；2.河南省高性能轴承技术重点实验室，河南 洛阳 471039；3.滚动轴承产业技术创新战略联盟，河南 洛阳 471039；4.军工轴承技术创新团队，河南 洛阳 471039；5.北京控制工程研究所，北京 100086）

位标器陀螺转子系统所用的高精密球轴承承载小、应用环境清洁度高，其失效形式往往不是疲劳失效，而是运转不稳定导致的精度失效，轴承的运转稳定性已成为制约该类轴承使用寿命的关键技术。

保持架通常是轴承结构中最薄弱的环节，轴承运转失稳一般都会反映到保持架上。实践表明，只要解决了保持架运转稳定性问题，也就解决了轴承的运转稳定性难题，故国内外学者纷纷将研究聚焦于此问题上。文献［1］通过试验验证了航天用轴承方形兜孔保持架适用于边界润滑条件，而圆形兜孔保持架更适用于充分润滑条件；文献［2］认为改变兜孔间距可以减小轴承力矩噪声；文献［3］提出通过减小兜孔间隙／引导间隙，可以有效降低保持架因不稳定运动引起的噪声；文献［4］通过试验得出了适用于动量轮轴承保持架的最佳引导间隙和兜孔间隙；文献［5］通过正交优化试验得出了适用于陀螺马达轴承保持架的最佳引导间隙和兜孔间隙；文献［6］通过试验得出了适用于专用电机轴承的最佳保持架间隙比；文献［7］认为在规定的工况条件下，保持架不稳定性与兜孔间隙和引导间隙有明确的相关性；文献［8］以喷油润滑条件下的发动机轴承为研究对象，编制了球轴承刚柔多体动力学分析程序，实现了柔体保持架的动态性能仿真；文献［9］运用盒维数理论来判定保持架的运转稳定性，并分析了轴承结构参数对保持架运转稳定性的影响。上述分析均针对特定轴承，通用性不足，缺乏沟道涂油润滑方式下的非金属保持架动态性能影响方面的仿真研究。

1 保持架动力学数学模型

轴承在运转过程中，保持架、钢球均具有6个自由度，保持架运动受钢球与保持架间作用力（法向碰撞力、切向摩擦力）、引导挡边与保持架引导面间作用力（法向碰撞力、切向摩擦力）、润滑油对保持架的作用力的综合影响［10］。任何一个小的激振力，都会对保持架的动态性能产生影响。因此，能否精确求解保持架的实际受载决定保持架动态性能仿真结果的可信度。

考虑到位标器陀螺转子系统用轴承润滑方式为沟道涂油润滑，计算模型中可以忽略润滑油对保持架的作用力。建立保持架受力模型时，需对钢球与兜孔间碰撞力、摩擦力和保持架与套圈引导面间的碰撞力、摩擦力进行精确求解。

2个滚动零件间的相对滑动速度引起的润滑剂与滚动零件之间的摩擦力，又称拖曳力。轴承转动时钢球-沟道间的拖曳力是钢球发生加速、减速、打滑、偏斜的关键因素，从而影响到保持架的运转稳定性。因此，计算钢球与保持架的受力，首先需明确钢球与沟道间的拖曳力的计算模型。润滑剂在高压接触区中受速度、温度、载荷条件的综合影响，具有非常复杂的物理特性，拖曳力的计算一直以来都是一个难点，文中拖曳力计算模型引用了文献［11］的研究成果。

1.1 钢球与保持架兜孔间的相互作用

轴承在运转过程中，钢球与兜孔中心的位置差会导致钢球与兜孔间产生作用力。在径向平面内，兜孔中心Op超前于钢球中心Ob（如Op1超前Ob1）和滞后于钢球中心Ob（如Op2滞后Ob2）的情况如图1所示。

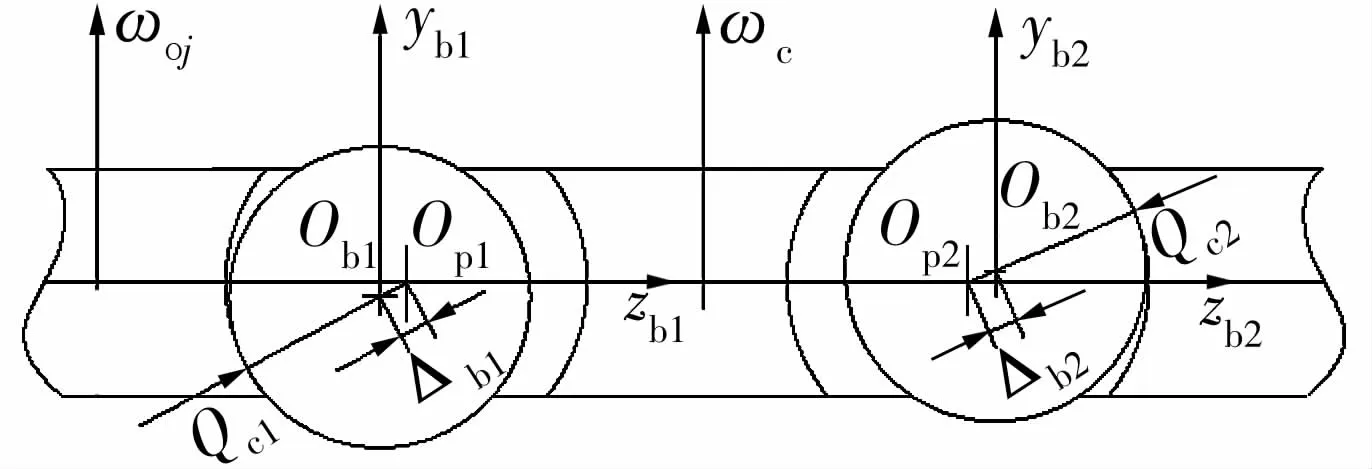
图1 钢球中心和保持架兜孔中心的位置关系Fig.1 Positional relationship between ball center and cage pocket center

图中：ωoj为第j个钢球的公转角速度；ωc为保持架公转角速度；Op超前时，ωoj小于ωc，保持架兜孔推动钢球，Δbj为正；Op滞后时，Δbj为负，钢球推动保持架兜孔表面。

位标器陀螺转子系统用轴承为超薄壁轴承，保持架材料为聚酰亚胺，壁厚为0.75 mm，宽度为2.2 mm，计算钢球与兜孔之间的法向力需综合考虑保持架薄壁特征、非金属材料特性以及润滑状态。钢球与兜孔之间法向力为

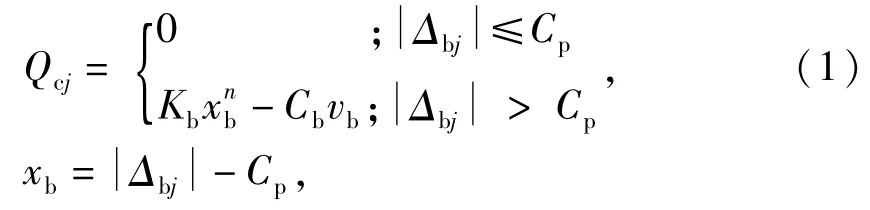
式中：Cp为保持架兜孔间隙；Kb为钢球与兜孔间的接触刚度，其值可由有限元法求得；xb为钢球与兜孔的接触深度；n为接触力指数，文中取1.5；Cb为接触阻尼，文中取接触刚度的1%；vb为钢球与兜孔接触时钢球的速度。钢球与兜孔间摩擦力Fcj＝μQcj，摩擦因数μ取0.02。

1.2 套圈引导面与保持架之间的相互作用

套圈引导面与保持架之间的法向力为

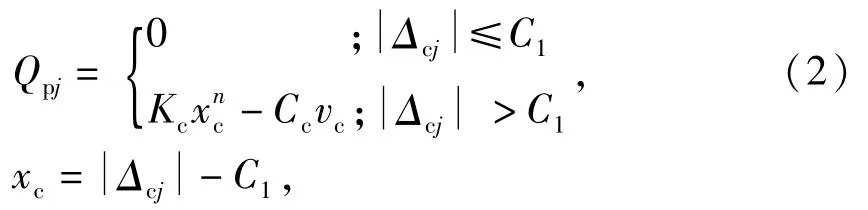
式中：C1为保持架引导间隙；Kc为保持架的结构刚度，可由有限元法求得；Δcj为保持架中心与轴承中心的距离；xc为保持架与套圈引导面间的接触深度；Cc为保持架结构阻尼，取结构刚度的1%；vc为保持架与引导面接触时保持架的速度。在计算保持架与引导面间摩擦力时，摩擦因数取0.02。

2 仿真结果及分析

以46／24.4型深沟球轴承为例进行动力学仿真分析，轴承结构参数见表1，钢球及保持架的材料参数见表2。保持架引导方式为外圈引导。假设轴承工作的环境温度为25℃，外圈转速为7 200 r／min，径向载荷为 Fr＝0 N，轴向载荷为Fa＝5.0 N。

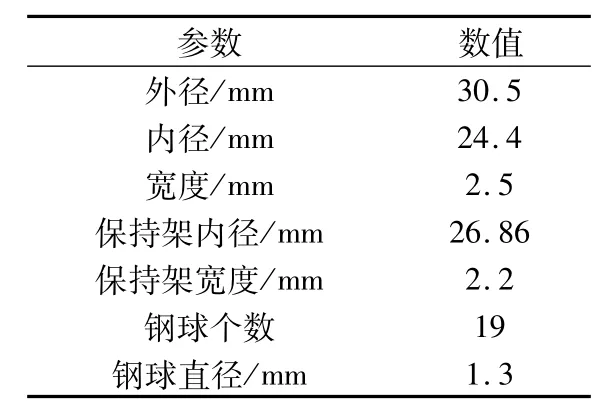
表1 轴承结构参数Tab.1 Structural parameters of bearing

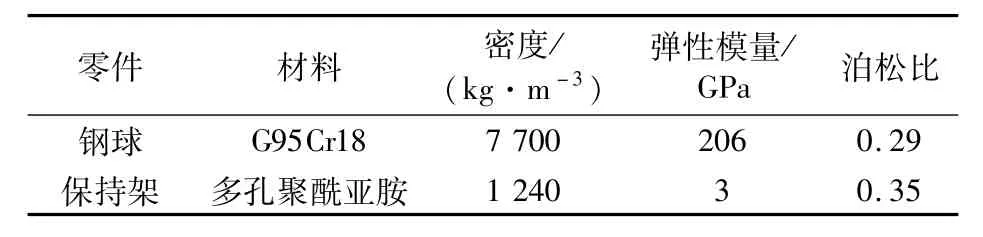
表2 材料参数Tab.2 Materials parameters

2.1 间隙对保持架打滑率、冲击力的影响

保持架打滑率反映了保持架实际转速与理论转速间的差值，打滑率越小，保持架实际转速与理论转速越接近，钢球与沟道间的滚动成分越多，滑动成分越少，由滑动导致的摩擦与磨损越小，越利于保持架运转稳定。

12种不同的兜孔间隙、引导间隙组合下，轴承保持架的打滑率、轴承引导面与保持架间的冲击力的计算结果见表3。

根据打滑率和轴承引导面与保持架间的冲击力，对方案的优化结果分别为：f＞d＞c＞k＞h和a＞k＞l＞i＞h，综合考虑这2个优化指标，方案 k最优。

2.2 间隙对保持架质心轨迹的影响

在表3的间隙组合下，保持架质心在径向平面内的运动轨迹如图2所示。由图可知：纯轴向载荷下，保持架质心轨迹为圆形；引导间隙越大，保持架质心轨迹半径越大，且轨迹半径约为引导间隙的一半。保持架质心从起始（轴承中心）位置处进入轨迹圆的难易程度及质心轨迹的发散程度均可以反映该间隙下保持架的运转稳定性，图2a，2b，2c，2f，2i，2j，2l中，保持架质心自起始位置进入轨迹圆前轨迹十分紊乱，图2e，2h的质心轨迹较为发散，只有图2k的保持架质心进入轨迹圆较为“容易”，且轨迹圆非常规则。因此，从质心轨迹发散程度、进入轨迹圆难易程度2个角度综合评价，方案k最优，该结论从侧面说明了优化结果的正确性。

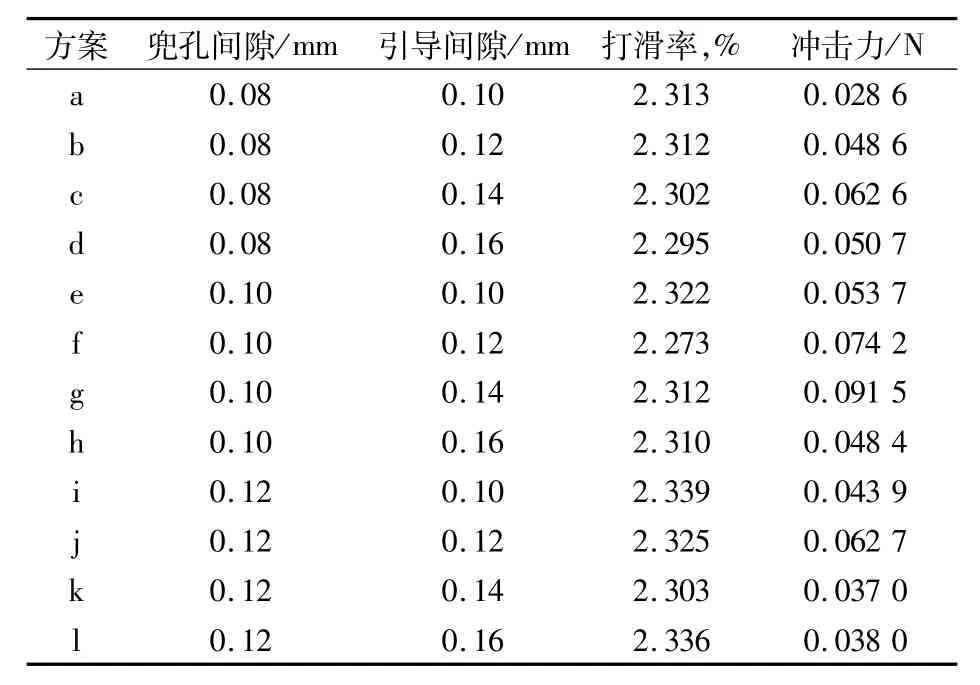
表3 不同间隙下保持架的打滑率、冲击力Tab.3 Slip ratio and impact force of cage under different clearances

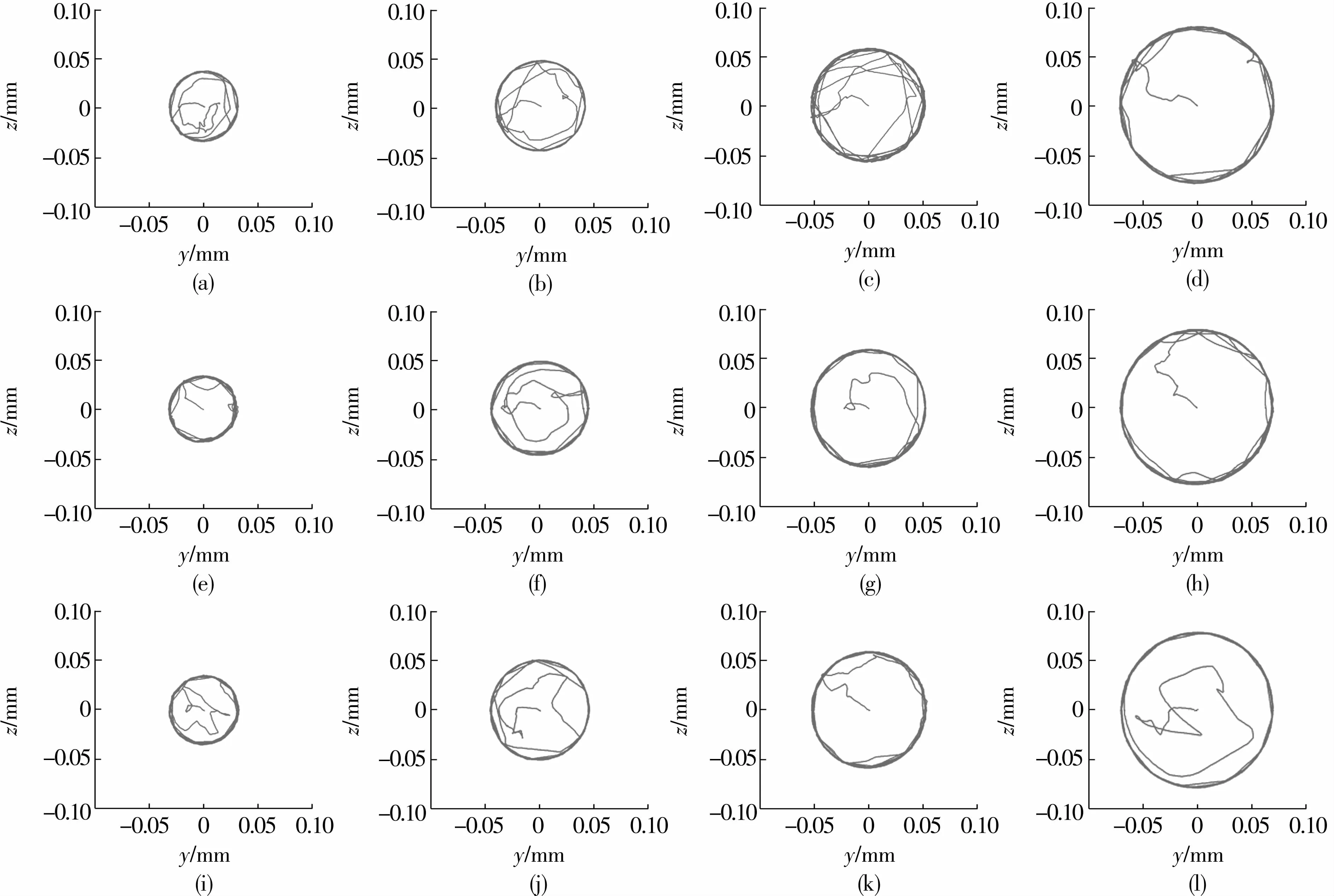
图2 不同间隙下保持架径向平面内的质心轨迹Fig.2 Mass center trajectory of cage in radial plane under different clearances

3 试验验证

为验证仿真分析的正确性，结合现有轴承振动-寿命试验台，分别选用方案h、方案k进行轴承动态性能对比试验。

装入2种保持架后轴承振动如图3所示，由图可知，方案k的最大和最小振动值分别为58.8，57.6 dB，波动范围为2.08%；方案h的最大和最小振动值分别为61.7，59.3 dB，波动范围为4.05%。与方案k相比，采用方案h时的轴承振动值和波动范围较大。

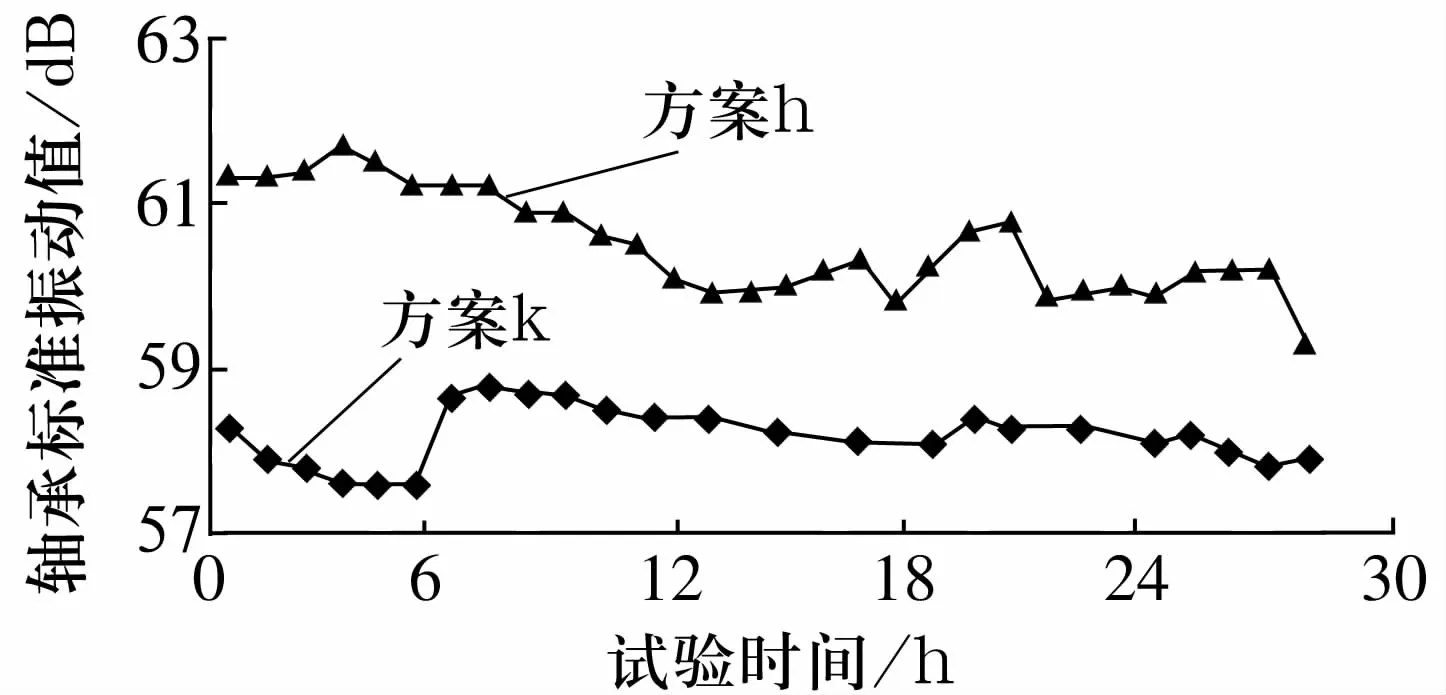
图3 方案h，k下轴承振动值变化趋势Fig.3 Variation trends of bearing vibration value under plan h，k

试验后保持架的磨损如图4所示，方案k保持架磨损较轻，而方案h保持架外径面、兜孔处磨损较严重，说明采用方案k轴承的运转稳定性要全面优于方案h。由于试验轴承套圈、钢球完全一致，2种试验结果的差异由保持架间隙不同造成，因此，可认为仿真分析是正确的。

图4 试验后保持架磨损图Fig.4 Diagram of cage wear after experiment

4 结束语

以位标器陀螺转子系统用球轴承为研究对象，考虑非金属保持架的薄壁特性，结合有限元分析方法，建立了沟道涂油润滑方式下球轴承非金属保持架动力学仿真数学模型。分析了保持架兜孔间隙、引导间隙对保持架动态性能的影响规律，据此优化了保持架兜孔间隙、引导间隙，并通过试验验证了仿真分析的正确性，为该类轴承保持架的动态性能分析提供了参考。研究不足之处在于仿真模型中简化了轴承钢-聚酰亚胺的摩擦因数，后续有待进一步研究。