改进的VMD方法及其在转子故障诊断中的应用

刘尚坤，　唐贵基

(华北电力大学 能源动力与机械工程学院，河北保定 071003)



改进的VMD方法及其在转子故障诊断中的应用

刘尚坤，唐贵基

(华北电力大学 能源动力与机械工程学院，河北保定 071003)

摘要：针对转子系统油膜失稳的诊断问题以及变分模态分解(VMD)的端点效应问题，提出一种利用互信息准则进行波形匹配和端点延拓的改进VMD方法，并通过分析各分量的Hilbert谱诊断油膜失稳状态.结果表明：该方法具有良好的多分量信号分解能力和端点效应抑制效果，能有效诊断出油膜涡动的发生时刻以及发展变化特点；当单盘转子发生1阶油膜振荡时，频谱中转频和振荡频率的幅值突出，同时会出现与两者相关的组合频率成分，对准确、可靠地诊断油膜失稳具有重要意义.

关键词：转子故障诊断； 油膜失稳； 变分模态分解； 端点效应； 时频分析

油膜失稳是大型汽轮发电机组在启停和运行中需要高度关注的问题，一旦油膜涡动转化为油膜振荡，会使机组产生共振，可能导致各部件松动甚至轴系毁坏.因此，准确诊断早期故障并采取措施对设备安全稳定运行具有重要意义.

转子系统油膜失稳的实质是发生了自激振动，通常由半速油膜涡动演变为油膜振荡[1]，在此过程中振动信号常表现出非平稳、非线性的特点，如何提取振动信号中各个分量的时频分布信息是故障诊断的关键[2].Guo等[3]采用希尔伯特-黄变换(Hilbert Huang Transform，HHT)分析了横向裂纹转子的瞬态响应特性；向玲等[4]利用HHT分析了汽轮发电机组轴系扭振的时频特征，但由于经验模态分解 (Empirical Mode Decomposition, EMD)存在模态混叠、过包络和欠包络等问题，从而影响HHT的分析效果[5]；唐贵基等[6]采用希尔伯特振动分解(Hilbert Vibration Decomposition，HVD)诊断了转子系统油膜涡动故障，但没有讨论故障早期识别问题以及油膜振荡时的频率特征；滕伟等[7]采用Gabor变换成功提取了实际汽轮机振动信号半速涡动频率，但Gabor变换的时频窗是不变的，难以同时保持对信号中高频部分和低频部分的高分辨率.

Dragomiretskiy等[8]提出了一种新的多分量信号自适应分解方法——变分模态分解(VMD)，该方法采用迭代方式搜寻变分模型最优解来确定每个分量的中心频率及带宽，最终自适应地实现信号的频域剖分以及各分量的分离.笔者尝试将其应用于转子系统油膜失稳故障分析，针对VMD存在的边界效应影响分析精度问题，利用互信息准则通过波形匹配和端点延拓对其加以改进，并对分解得到的各分量进行Hilbert变换得到时频图，然后根据时频分布特征判断油膜涡动的发生时刻和发展变化特点以及分析转子油膜振荡的频谱特征.

1变分模态分解

VMD将本征模态函数(IMF)定义为一个调幅-调频信号，即

(1)

VMD模型的构造和求解涉及3个重要概念: 经典维纳滤波、Hilbert变换和频率混合.

假设多分量信号f由K个有限带宽的IMF分量uk组成，且各IMF的中心频率为ωk，VMD方法建立的约束变分模型为

(2)

式中：{uk}表示分解得到的K个IMF分量集合，{uk}={u1,…,uK}；σ(t)为脉冲函数;{ωk}表示各分量的中心频率集合,{ωk}={ω1,…,ωK}.

该模型建立过程中，首先对每个uk(t)进行Hilbert变换得到解析信号并计算单边谱，再乘以指数函数e-jωkt，将所估计的uk(t)的中心频带调制到基频带上，最后计算该调制信号梯度的平方L2范数，估计出各模态信号带宽.

为求上述约束变分问题的最优解，需将其转换为非约束变分问题，为此引入如下形式的增广Lagrange函数：

(3)

式中：α为二次项的惩罚参数；λ为Lagrange乘子;〈·〉表示内积运算.

利用乘子交替方向算法求解上述问题，不断更新各分量及其中心频率，最终求得的式(3)的鞍点即为原问题的最优解，而所有的分量可从频域中通过式(4)获得：

(4)

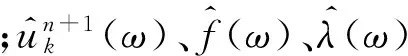
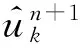
(5)

VMD方法具体实现过程如下：

(2)n=n+1，开始循环.

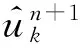
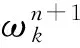
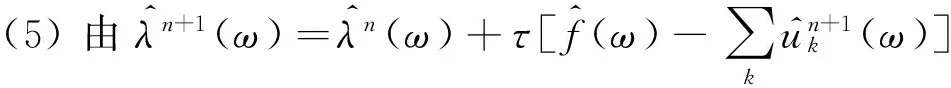
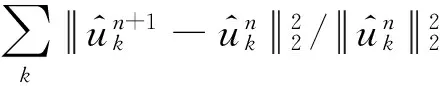
VMD方法的信号分解结果主要受分量个数K和惩罚参数α的影响[9]，由于实际待分析的信号各不相同，如何对VMD方法的参数进行自适应选择仍在讨论之中.本文K、α的设定值是选择不同设定下的最佳分解效果.

2基于互信息准则的VMD端点效应改进

虽然VMD方法采用非递归的方式分解出各分量，但由于信号的截断以及Hilbert变换的使用均会产生边界效应，影响分析精度，而解决边界效应的一般方法是对信号进行边界延拓.互信息(MI)由信息论中熵的概念引申而来，采用2个随机变量间不确定度的差值来表示，能够表明其统计相关性.互信息I(X,Y)的表达式如下：

(6)

式中：H(Y)为Y的熵；H(Y|X)为已知X时Y的条件熵.

式(6)表明，X与Y的相关性越强，条件熵H(Y|X)越小，则互信息I(X,Y)越大[10].将其用于判断原信号中子波形间的相关程度，并取互信息值最大的子波形为最佳匹配波形，然后对其进行信号边界延拓，解决端点效应问题.具体步骤如下：

(1) 设离散信号x(t)有n个样本数据，其中有m个极大值点{M1，M2，…，Mm}和p个极小值点{N1，N2，…，Np}.如图1所示，以左边界第一极值点为极大值点为例，选取左端点S1到第2个极值点N1间的波形为研究对象，记为W1.

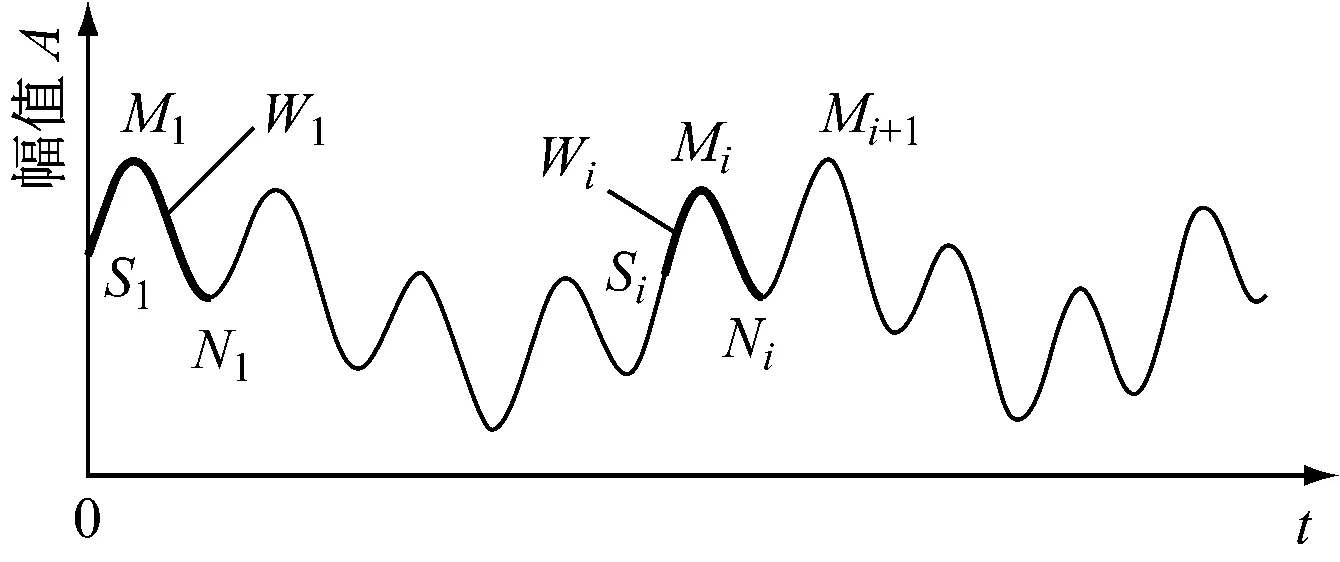
图1　波形匹配示意图

(2) 分别以Mi(2≤i≤m)作为与M1的位置对应点，截取与W1等长的子波Wi，即保证Mi在Wi中相对Si的时序位置与M1在W1中相对S1的时序位置一致，如图1中粗实线所示.

(3) 然后计算Wi与W1的互信息值Ii，并作为各个子波形与W1的匹配系数，取匹配系数最大的子波Wi作为W1的最佳匹配波形，将该子波Wi前适当长度的数据延拓到x(t)左侧.

(4) 利用同样的原理延拓信号的右边界.

(5) 将延拓后的信号进行VMD分解，根据原信号长度及其在延拓后信号中对应的位置截取数据.

采用改进VMD方法进行故障诊断的主要步骤如下：

(1) 利用互信息准则对原信号进行波形匹配和端点延拓以解决端点效应问题，再进行VMD分解，得到K个IMF分量.

(2) 通过Hilbert变换分别计算这K个IMF分量的瞬时幅值和瞬时频率，根据原信号的长度及其在延拓信号中对应的位置截取时频分析结果.

(3) 分析Hilbert谱中的各频率特征，判断是否存在故障特征频率，以实现故障诊断.

3仿真信号分析

构造1个多分量信号x(t)，其中分量x1(t)为频率接近的2个正弦信号，同时含有调频信号x2(t)以及在2个不同时间段频率单一的和信号x3(t)，如式(7)所示.图2为各分量及合成信号x(t)的时域波形.图3为直接利用VMD方法(K=5，α=1 500)进行分解得到的各个分量的Hilbert谱.由图3可知，VMD方法能较好地把频率接近的250 Hz与270 Hz、调频分量以及频率突变分量进行有效分离，但各个分量也出现了明显的端点效应，影响分析精度.图4为采用本文改进的VMD方法处理端点效应后分析得到的Hilbert谱.由图4可知，各个分量的端点效应得到了较好的抑制.

(7)

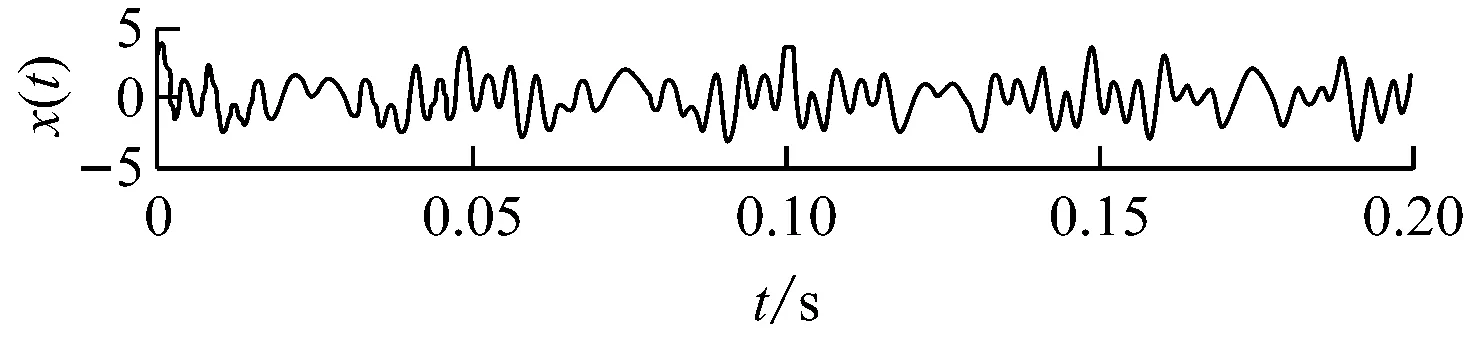
图2　仿真信号的时域波形

为了验证本文方法的效果，图5给出了采用HHT进行分解得到的各个分量.由图5可知，x1(t)中频率接近的2个正弦分量没有得到分离，同时分离的x2(t)的调频信息不够明确，虽然x3(t)的突变频率能基本识别，但检测出的各个分量之间均出现了不同程度的模态混叠，较本文方法分析效果差.

图3　VMD方法直接分析仿真信号得到的Hilbert谱

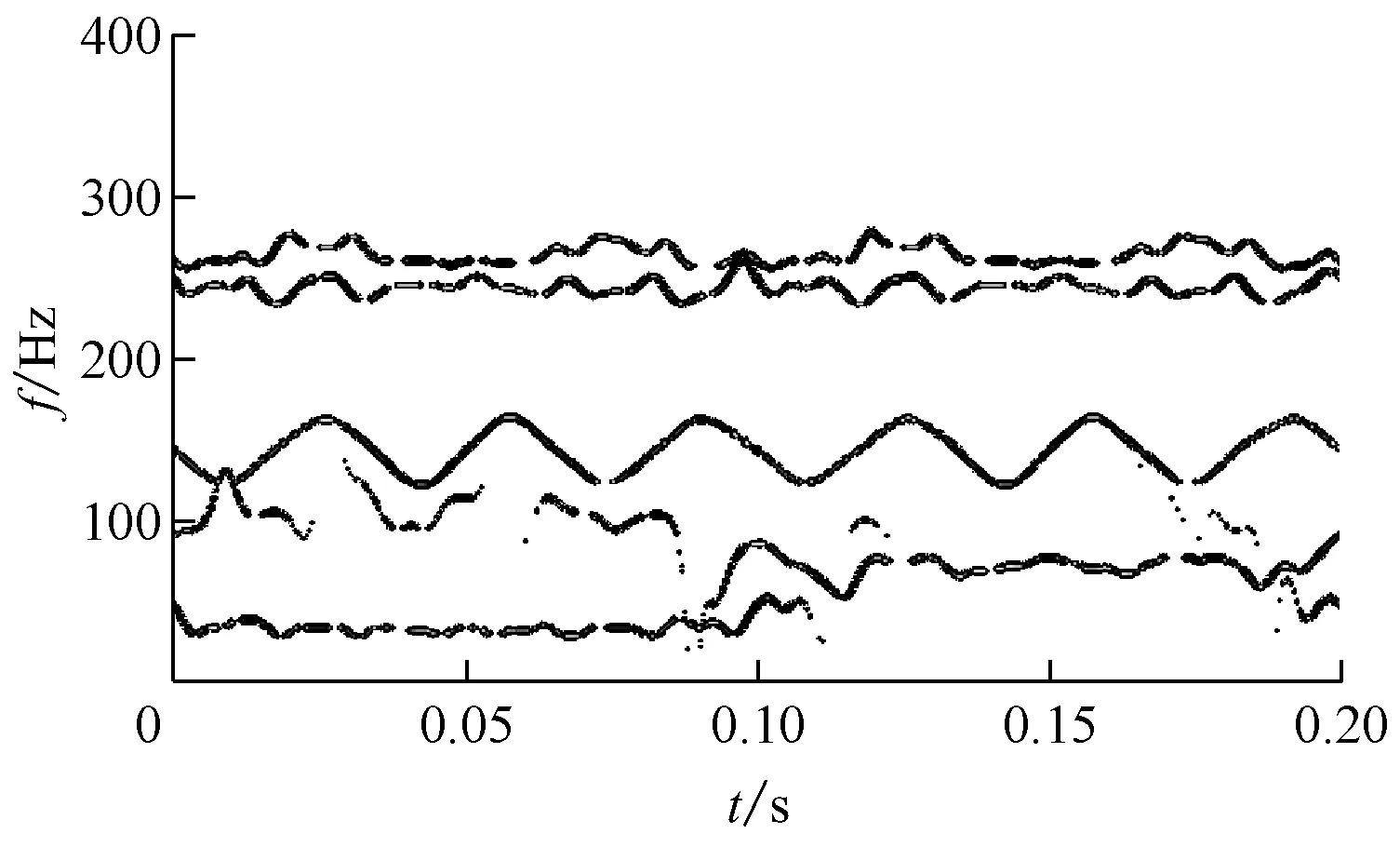
图4　改进VMD方法分析仿真信号得到的Hilbert谱

图5　HHT分析仿真信号得到的Hilbert谱

4油膜失稳试验分析

试验装置采用Bently RK-4转子系统故障模拟实验台，配有信号前置适配器、转速控制调节装置和进行油膜失稳所需的轴承和油泵系统，能实现油膜涡动和油膜振荡试验.在单盘转子两侧安装电涡流传感器以测量转轴径向振动位移，由美国Iotech公司生产的ZonicBook/618E采集转子在升速过程中的振动信号，采样频率为1 280 Hz.经多次试验，转子实验台在转速为1 650 r/min附近发生油膜涡动，在3 750 r/min附近发生油膜振荡，振荡频率约为31 Hz，取转子各试验状态下2 048个采样点加以分析.

4.1油膜涡动分析

图6为早期油膜涡动的时域波形和频谱图.由图6可知，时域波形中没有发生明显的变形，频谱图中只有转频27 Hz突出，不能明确诊断是否发生了油膜涡动.采用改进VMD方法(K=5，α=500)对该时段信号进行VMD分解后的Hilbert谱如图7所示.从图7可以看出，转频27 Hz幅值突出，650点之前为油膜涡动尚未完全形成阶段，之后涡动频率稳定在13 Hz，在1 700点后又发生了涡动频率波动，明确显示了油膜涡动的发生时刻和发展过程，且涡动早期幅值较小，同时图中还出现了幅值较小的2倍转频成分，端点效应也得到了较好的抑制.图8给出了采用VMD方法直接分析早期油膜涡动得到的Hilbert谱，图中存在较为明显的端点效应问题.

(a) 时域波形

(b) 频谱图

图7　改进VMD方法分析早期油膜涡动得到的Hilbert谱

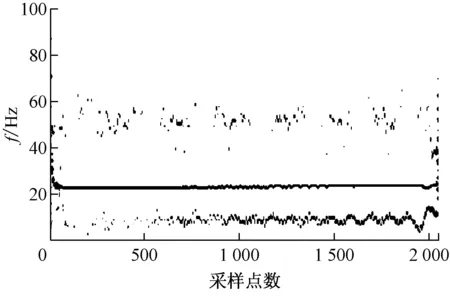
图8　VMD方法直接分析早期油膜涡动得到的Hilbert谱

图9为后期油膜涡动的时域波形和频谱图.从图9可以看出，时域波形发生了较明显的变形，频谱图中只能显示涡动频率21 Hz的幅值超过转频44 Hz的幅值，而且缺少时间信息.图10为采用改进VMD方法分析后期油膜涡动得到的Hilbert谱.从图10不仅能看出涡动频率21 Hz的幅值较转频44 Hz的幅值突出，而且能够表明幅值和频率随时间的变化情况.图10中同时出现了涡动频率与转频的小幅值和频率成分.

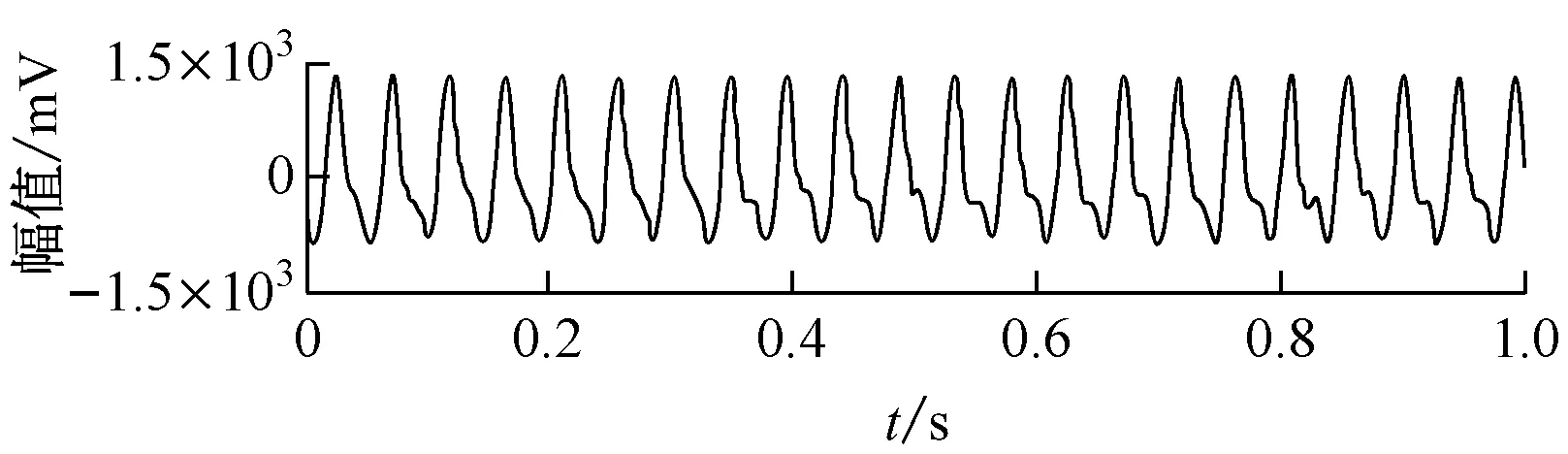
(a) 时域波形

(b) 频谱图

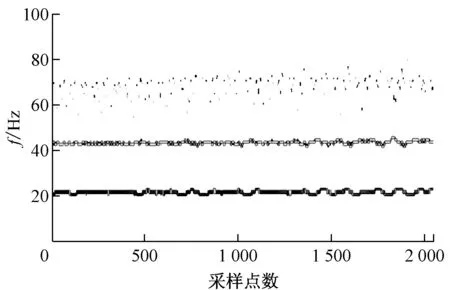
图10　改进VMD方法分析后期油膜涡动得到的Hilbert谱

4.2油膜振荡分析

试验中当转速上升至4 560 r/min时，转子系统表现出共振明显的油膜振荡现象，时域波形和频谱图如图11所示.图12为采用改进VMD方法(K=9，α=300)分析得到的三维时频图，其中转频1X(表示1倍转频，即76 Hz)和振荡频率fw(30.5 Hz)的幅值突出.同时图12中存在1/2fw(15 Hz)、1X-fw(45 Hz)、1X+fw(106 Hz)、1X+3/2fw(121 Hz)和2X(155 Hz)频率成分，据此能准确可靠地诊断转子发生了油膜振荡，而图11频谱图中只有转频和振荡频率的幅值突出，只能初步诊断发生了油膜振荡.由图12可知，单盘转子在1阶油膜失稳时，频率成分以转频1X和振荡频率fw为主，同时会出现与两者相关的组合频率成分.此频谱特征与双盘转子在两圆盘受同向偏心载荷时的1阶油膜振荡频谱特征[11]相似，这是因为两者所受载荷等效.图13为采用VMD方法直接分析油膜振荡得到的三维时频图.图13中虽然也能够分解得到各个分量，但都出现了不同程度的端点效应问题.

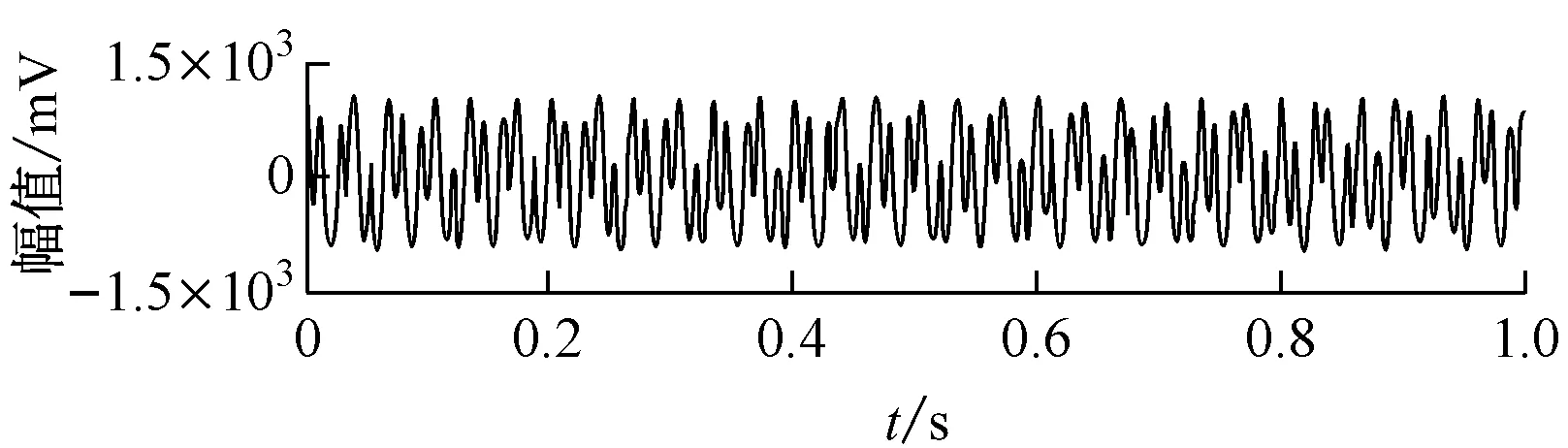
(a) 时域波形

(b) 频谱图

图12　改进VMD方法分析油膜振荡的三维时频图

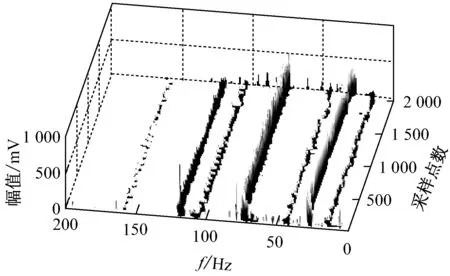
图13　VMD方法直接分析油膜振荡的三维时频图

为了进一步对比分析效果，图14给出了采用HHT分析油膜振荡得到的Hilbert谱.从图14可以看出，其中3处出现了明显的模态混叠，虽然分析出振荡频率30.5 Hz及其二分频15 Hz频率成分，但转频出现明显的调制现象，其他组合频率也不能分解出来，比本文方法的分析效果差.

5结论

(1) VMD作为一种新的多分量信号分解方法，采用频域非递归的迭代求解方式，能有效避免模态混叠问题，对其端点效应采用互信息准则选取匹配子波形段并进行边界延拓，然后结合时频图有效诊断出油膜失稳故障.对比分析结果表明，改进的VMD方法优于HHT分析方法，具有一定的工程应用价值.

图14　HHT分析油膜振荡得到的Hilbert谱

(2) 单盘转子发生1阶油膜振荡时的频谱中除主导频率(转频和振荡频率的幅值较突出)外，还会出现与两者相关的组合频率成分，其频谱特征与双盘转子在两圆盘受同向偏心载荷时1阶油膜振荡的频谱特征基本相同，对提高油膜振荡诊断的准确性和可靠性有重要意义.

参考文献：

[1]唐贵基，向玲，朱永利. 基于HHT的旋转机械油膜涡动和油膜振荡故障特征分析[J]. 中国电机工程学报，2008, 28(2):77-81.

TANG Guiji, XIANG Ling, ZHU Yongli. Fault analysis of oil whirl and oil whip based on Hilbert Huang transform for rotor system[J]. Proceedings of the CSEE, 2008, 28(2): 77-81.

[2]URBANEK J, BARSZCZ T, ANTONI J. Time-frequency approach to extraction of selected second-order cyclostationary vibration components for varying operational conditions[J]. Measurement, 2013, 46: 1454-1463.

[3]GUO D, PENG Z K. Vibration analysis of a cracked rotor using Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2007, 21(8): 3030-3041.

[4]向玲，杨世锡，唐贵基，等. 汽轮发电机组轴系扭振的时频特征分析[J]. 动力工程学报, 2011, 31(9): 649-654,671.

XIANG Ling, YANG Shixi, TANG Guiji,etal. Time-frequency analysis on torsional vibration of turbo-generator shafts[J]. Journal of Chinese Society of Power Engineering, 2011, 31(9): 649-654, 671.

[5]向玲，鄢小安. 汽轮机转子故障诊断中LMD法和EMD法的性能对比研究[J]. 动力工程学报, 2014, 34(12): 945-951.

XIANG Ling, YAN Xiaoan. Performance contrast between LMD and EMD in fault diagnosis of turbine rotors[J]. Journal of Chinese Society of Power Engineering, 2014, 34(12): 945-951.

[6]唐贵基，庞彬. 基于改进的希尔伯特振动分解的机械故障诊断方法研究[J]. 振动与冲击, 2015, 34(3): 167-171.

TANG Guiji, PANG Bin. Research for a mechanical fault diagnosis method based on improved Hilbert vibration decomposition[J]. Journal of Vibration and Shock, 2015, 34(3): 167-171.

[7]滕伟，安宏文，马志勇，等. 基于时频滤波的汽轮机半速涡动故障成分提取[J]. 振动与冲击，2015, 34(3): 178-182.

TENG Wei, AN Hongwen, MA Zhiyong,etal. Semi-speed oil whirl fault component extraction of steam turbine based on time-frequency filtering[J]. Journal of Vibration and Shock, 2015, 34(3): 178-182.

[8]DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014，62(3): 531-544.

[9]唐贵基，王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报，2015, 49(5): 73-81.

TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi'an Jiaotong University, 2015, 49(5):73-81.

[10]唐勇波，桂卫华，彭涛，等. 基于互信息变量选择的变压器油中溶解气体浓度预测[J].仪器仪表学报，2013, 34(7): 1492-1498.

TANG Yongbo, GUI Weihua, PENG Tao,etal. Prediction method for dissolved gas concentration in transformer oil based on variable selection of mutual information[J]. Chinese Journal of Scientific Instrument, 2013, 34(7): 1492-1498.

[11]马辉，李辉，唐玉生，等. 两种不同载荷形式下转子系统油膜失稳的数值研究[J]. 振动工程学报，2013, 26(1): 105-111.

MA Hui, LI Hui, TANG Yusheng,etal. Numerical research on oil-film instability in a rotor system under two types of load conditions[J]. Journal of Vibration Engineering, 2013, 26(1): 105-111.

Application of Improved VMD Method in Fault Diagnosis of Rotor Systems

LIUShangkun,TANGGuiji

(School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China)

Abstract：To diagnose the oil film instability of rotor systems and to solve the problem of end effect occurring in variational mode decomposition (VMD), an improved VMD method was proposed based on mutual information criterion to match the waveform and to extend the endpoints, so as to judge the instability status of the oil film by analyzing the Hilbert time-frequency spectrum of each component. Results show that the proposed method has strong decomposition capability to multi-component signals and has good inhibiting ability on the end effect, which is able to diagnose the occurrence moment and subsequent development of oil whirl. When the first-order oil whip occurs in a single disc rotor, the rotation frequency and whip frequency would become prominent in the spectrum, with simultaneous occurrence of their combination frequency components. Above research results may serve as a reference for accurate diagnosis of oil film instability.

Key words：rotor fault diagnosis; oil film instability; variational mode decomposition; end effect; time-frequency analysis

收稿日期：2015-08-07

修订日期：2015-09-09

基金项目：河北省自然科学基金资助项目(E2014502052)；中央高校基本科研业务费专项资金资助项目(2014MS156，2015XS120)

作者简介：刘尚坤(1979-),男，河北阜城人，讲师，博士，研究方向为机械设备状态监测与故障诊断.电话(Tel.)：0312-7523442；

文章编号：1674-7607(2016)06-0448-06中图分类号：TH165+.3

文献标志码：A学科分类号：470.30

E-mail：lsk1213@163.com.