基于锁相环电源噪声引起的周期抖动分析

朱　剑

(西安电子科技大学 电子工程学院，陕西 西安 710071)



基于锁相环电源噪声引起的周期抖动分析

朱剑

(西安电子科技大学 电子工程学院，陕西 西安 710071)

摘要针对电源噪声在时钟电路的锁相环中引起的抖动问题，通过分析周期抖动和相位抖动与电源噪声间的关系，提出了用于预测电源噪声引起的锁相环抖动峰峰值的计算公式。文中预测的抖动峰峰值与HSPICE的仿真结果间的误差最大为3%，说明了文中公式的有效性。

关键词锁相环；电源噪声；周期抖动

锁相环的工作原理[1-4]早在30年代就被提出，其本质上就是一个闭环反馈的控制电路。锁相环电路实现的功能是使输出信号(反馈信号)和输入信号(参考信号)在相位与频率上实现同步，它为系统的其他部分提供了一个干净而且稳定的时钟输出信号。锁相环可以产生倍频或分频输出时钟，被广泛应用于串行通信系统中。随着集成电路工作频率不断提升，锁相环的工作频率越来越高，电源噪声也逐渐增大[5]。然而从始至终，它的基本电路原理框架从未发生变化，最根本的理论依然是自动控制理论。因为闭环反馈系统达到百分之百的稳定是不可能的，总是存在一定的波动，加之电源噪声的影响，锁相环产生的抖动从自动控制原理角度来看也是无法规避的。本文通过采用贝斯特的《锁相环设计、仿真与应用》书中的锁相环模型[6]，建立锁相环的HSPICE模型[7]，深入探讨电源噪声对锁相环电路抖动的影响。由周期抖动表达式推出相位抖动表达式，可以利用周期抖动来计算相位抖动，并通过测量压控振荡器的抖动模拟数据对表达式的有效性进行了验证。接着提出了不同频率电源噪声引起的周期抖动表达式，说明周期抖动和电源噪声有着良好的线性关系。

1锁相环模型

锁相环由4个基本部分组成:鉴相器+电荷泵、低通滤波器、压控振荡器和分频器。框图如图1所示。鉴相器用于鉴别输入信号和反馈信号间的相位差，使反馈信号和输入信号在相位与频率上实现同步。电荷泵的作用是将鉴相器输出的数字信号变换为一个稳定模拟的输出电压，这个电压通过低通滤波器之后进入压控振荡器的工作频率[8]。低通滤波器用于滤除电荷泵输出信号中的高频分量，得到低频且近似于直流的控制信号。压控振荡器的关键性能参数有：中心频率、调节线性度、调节范围、电源与共模抑制、输出振幅、输出信号纯度、功耗等[9]。压控振荡器对噪声非常敏感，理想压控振荡器的输出频率是其输入电压的线性函数。电源噪声会影响压控振荡器的输出频率，进而影响输出信号的抖动值。

2周期抖动表示相位抖动的公式推导

图2所示为抖动[10]时钟波形和理想时钟波形进行对比，得到相位抖动的表达式为

Δtn=tn-Tn

(1)

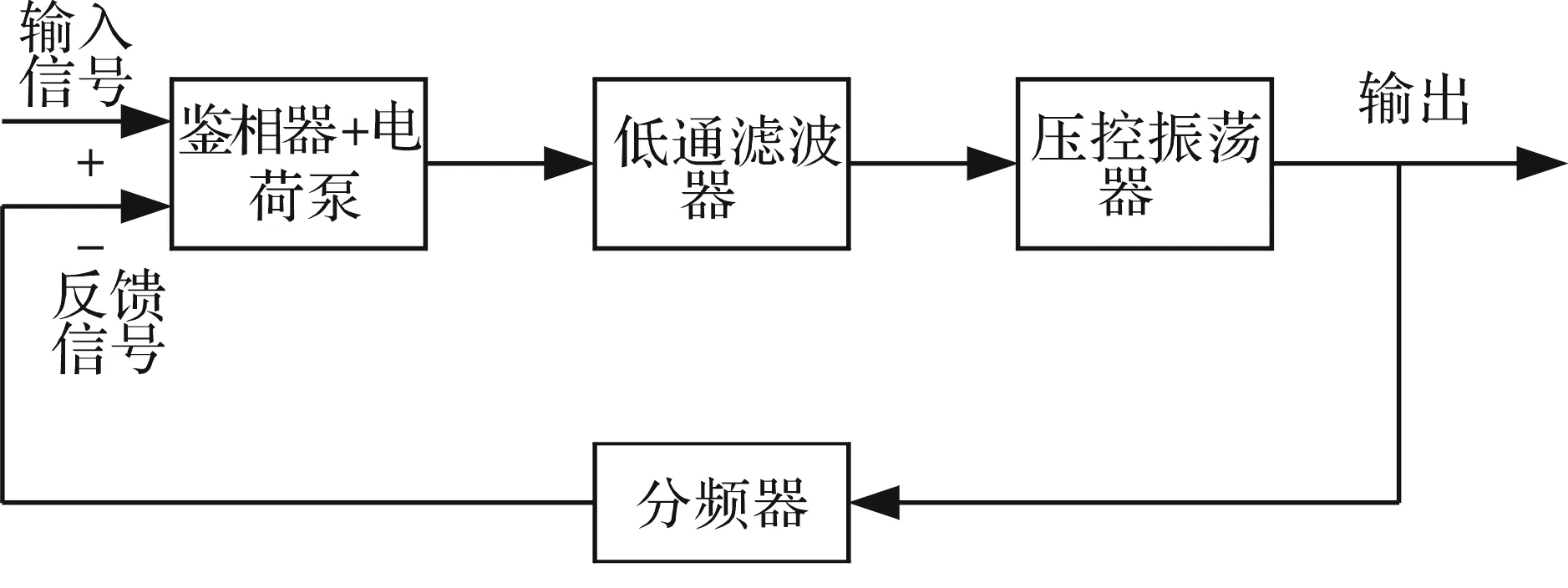
图1　锁相环结构

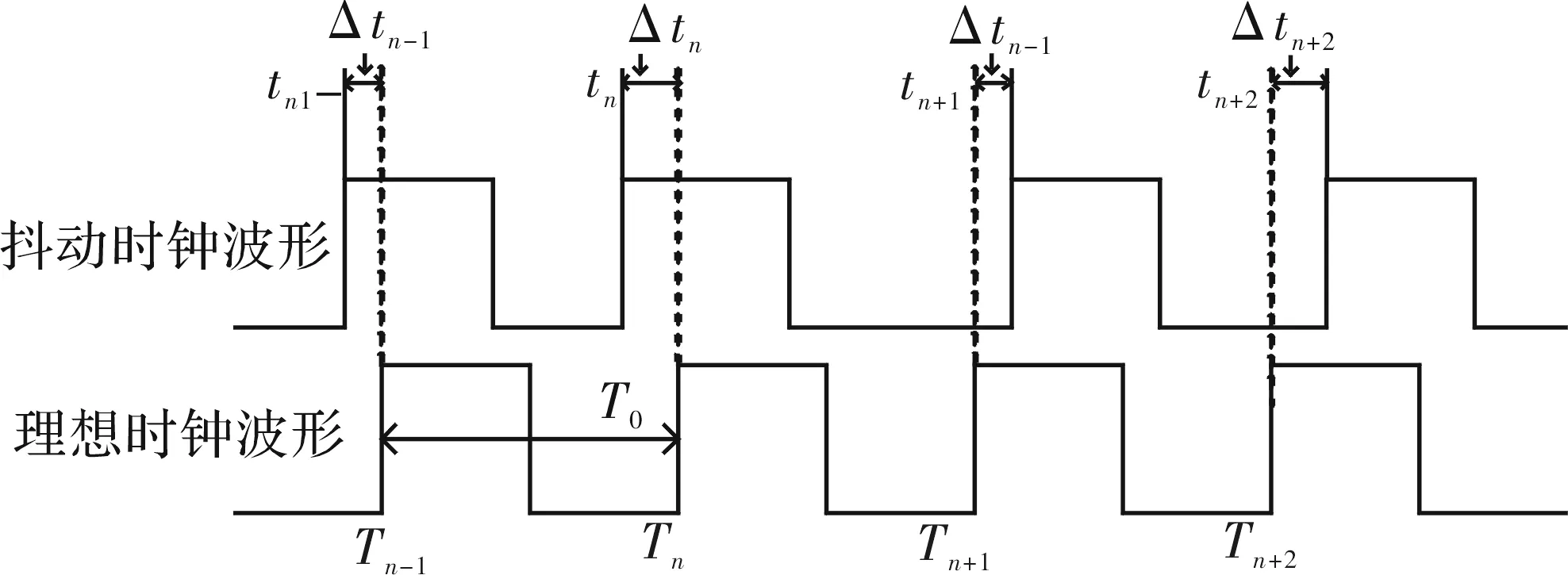
图2　抖动示意图

周期抖动的定义为

Δtpn=(tn-tn-1)-T0=

(tn-Tn)-(tn-1-Tn-1)=Δtn-Δtn-1

(2)

由上式可知，相位抖动可由周期抖动进行表示。根据式(2)，n时刻相位抖动的值为

(3)

其中，Δt1≠Δt2≠Δt3≠Δt4…≠Δtn，如果这些相位抖动相等，则周期抖动为零。图2中的抖动时钟波形的眼图如图3所示。

根据眼图的形成原理，在图3中信号眼图的抖动峰峰值表达式如下

J=max(ΔtRi)-min(ΔtRi)，i=1,2,…,n

(4)

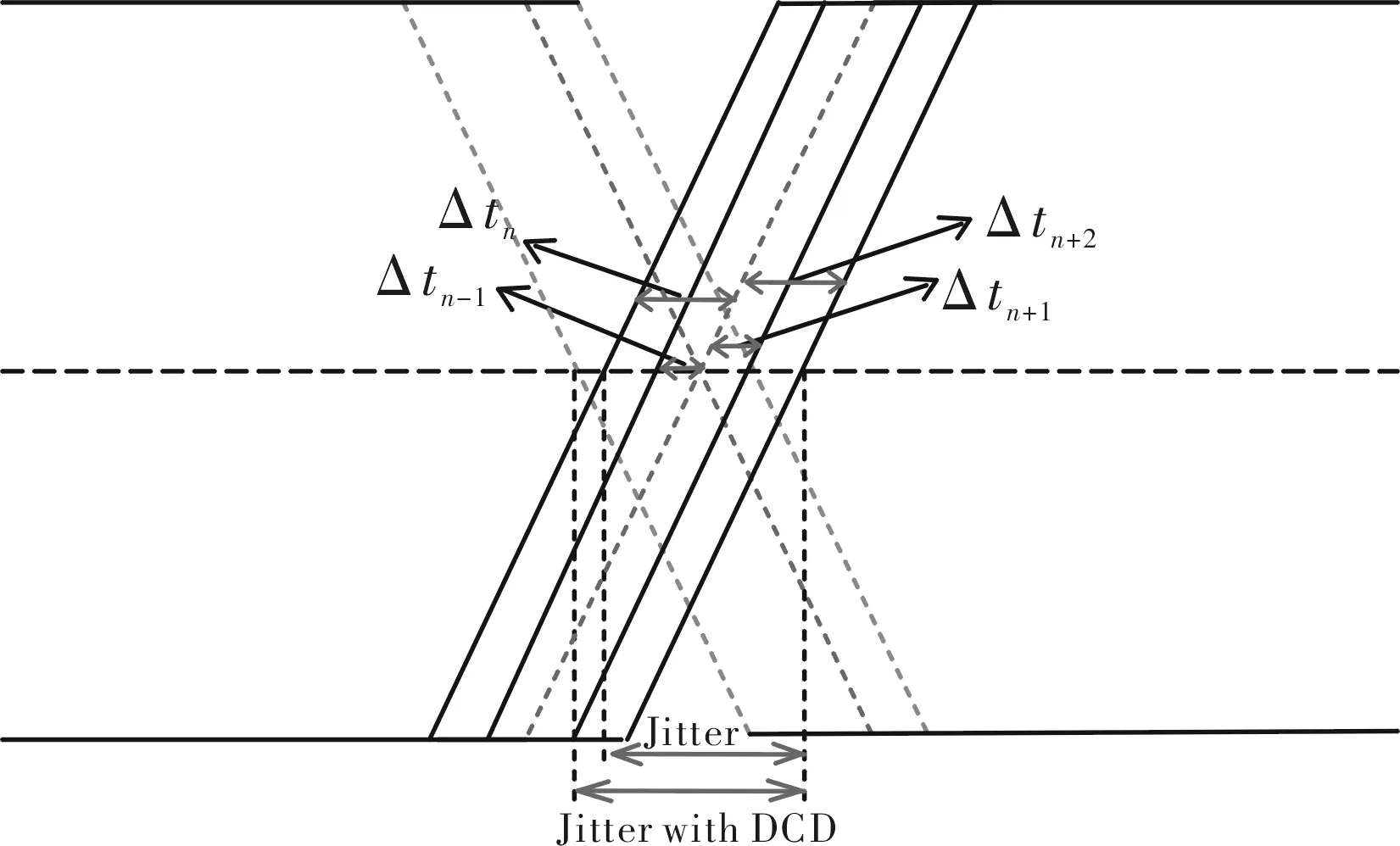
图3　时钟抖动的眼图

其中，ΔtRi表示信号上升边的周期抖动累计和；n表示上边的个数；J表示眼图中抖动峰峰值。其中占空比失真(DCD)能够影响眼图中抖动的大小，如图3所示。当存在占空比失真的时候，式(4)可以用式(5)来表示

J=max(ΔtRi,ΔtFi)-min(ΔtRi,ΔtFi)i=1,2,…,n

(5)其中，ΔtFi代表了下降边的周期抖动累计和。当占空比失真被减弱到可以忽略的时候，可以用式(4)来计算眼图中的抖动峰峰值。联合式(3)和式(4)，可得到

(6)

由式(6)可知，抖动峰峰值可以由相位抖动进行计算。当锁相环的工作频率为400MHz，电源噪声的频率为50MHz时，HSPICE仿真和由式(6)计算得到的锁相环输出信号的周期抖动峰峰值如表1所示。通过表1中的数据可以看出式(6)的正确性。

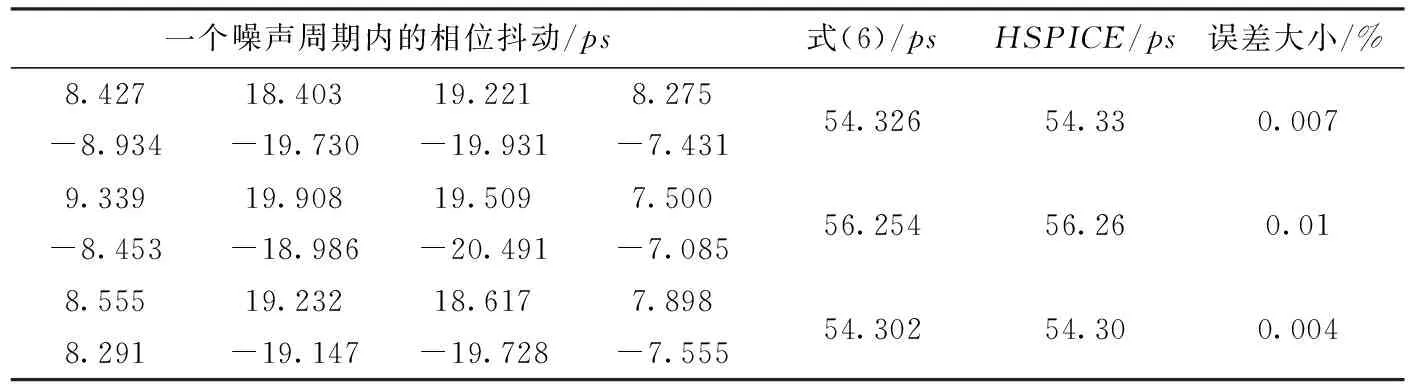
表1　HSPICE仿真结果和式(6)求得的周期抖动峰峰值

3电源噪声和周期抖动的关系

为得到电源噪声与抖动峰峰值间的关系，先研究压控振荡器中电源噪声和相位抖动间的关系，因为当设置压控振荡器的电源噪声为一个恒定值时，电源噪声是影响抖动的主要因素。

电源噪声、相位抖动和周期抖动的波形图如图4所示。为更容易地观察相位抖动和电源噪声间的关系，将相位抖动和周期抖动的幅度放大K倍，并且去除电源噪声和抖动间的相位差。从图4中可以看出周期抖动和电源噪声间具有良好的线性关系。

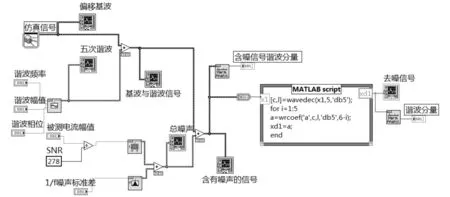
图4　抖动、周期抖动和电源噪声波形图

电源噪声是影响压控振荡器输出信号抖动的主要因素。然而，锁相环是一个复杂的非线性系统，有许多的因素导致抖动的产生。在闭环锁相环中，影响抖动的非理想因素除了电源噪声还有压控振荡器的控制信号。图5所示为闭环锁相环输出波形的眼图。仿真时间为10μs，电源参考电压的值是1V。电源噪声是频率为25MHz，振幅峰峰值为60mV的正弦信号，锁相环的工作频率为400MHz。当眼图采样时间为5μs时，抖动峰峰值为63ps，如图5(a)所示;当把眼图的采样时间调整为0.02μs时,抖动峰峰值为54.2ps，如图5(b)所示，闭环锁相环的抖动随着工作时间的延长而变大。

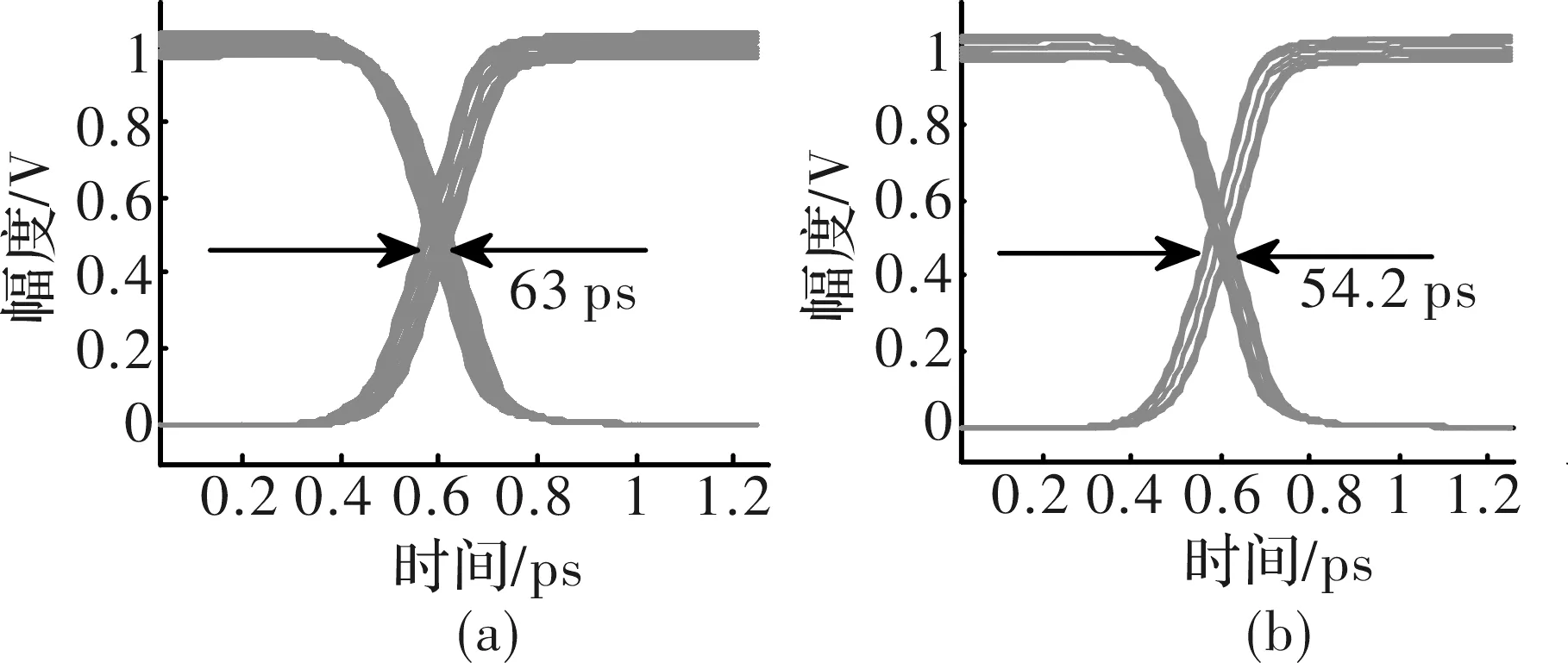
图5　锁相环输出波形的眼图

压控振荡器的控制电压也是影响锁相环抖动的一个因素，如果控制电压是不平滑的，并且有大的波动，对锁相环的抖动会有较大的影响。如图5所示，压控振荡器控制电压的波动会使锁相环的总抖动比一个噪声周期内大得多，图6所示为锁相环输出信号抖动随压控振荡器的控制电压变化趋势，从图中可以看出，锁相环输出信号的相位抖动随压控振荡器控制电压的波动产生剧烈变化。

图6　压控振荡器的控制电压对锁相环相位抖动的影响

图7所示为锁相环的周期抖动和压控振荡器控制电压的关系。从图中可以看出锁相环的周期抖动不会随着压控振荡器控制电压的变化有明显变化。

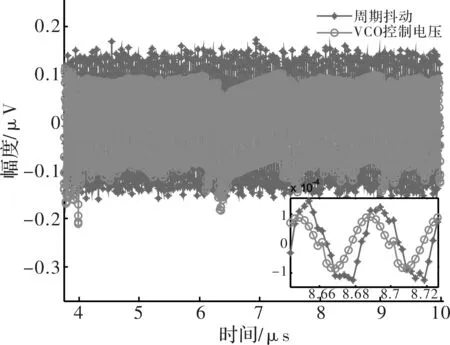
图7　锁相环的周期抖动与控制电压

定义一个系数K，它表示的是周期抖动和电源噪声幅度的比值。显然当电源噪声某点的值接近于零时，这个比值将会接近于无穷大，此时系数K没有意义，正如图5所示。为确保预测的准确性，删除电源噪声和周期抖动接近于零的数值，即将较大的系数K设置为零。设置后计算得到系数K的平均值如图8所示。

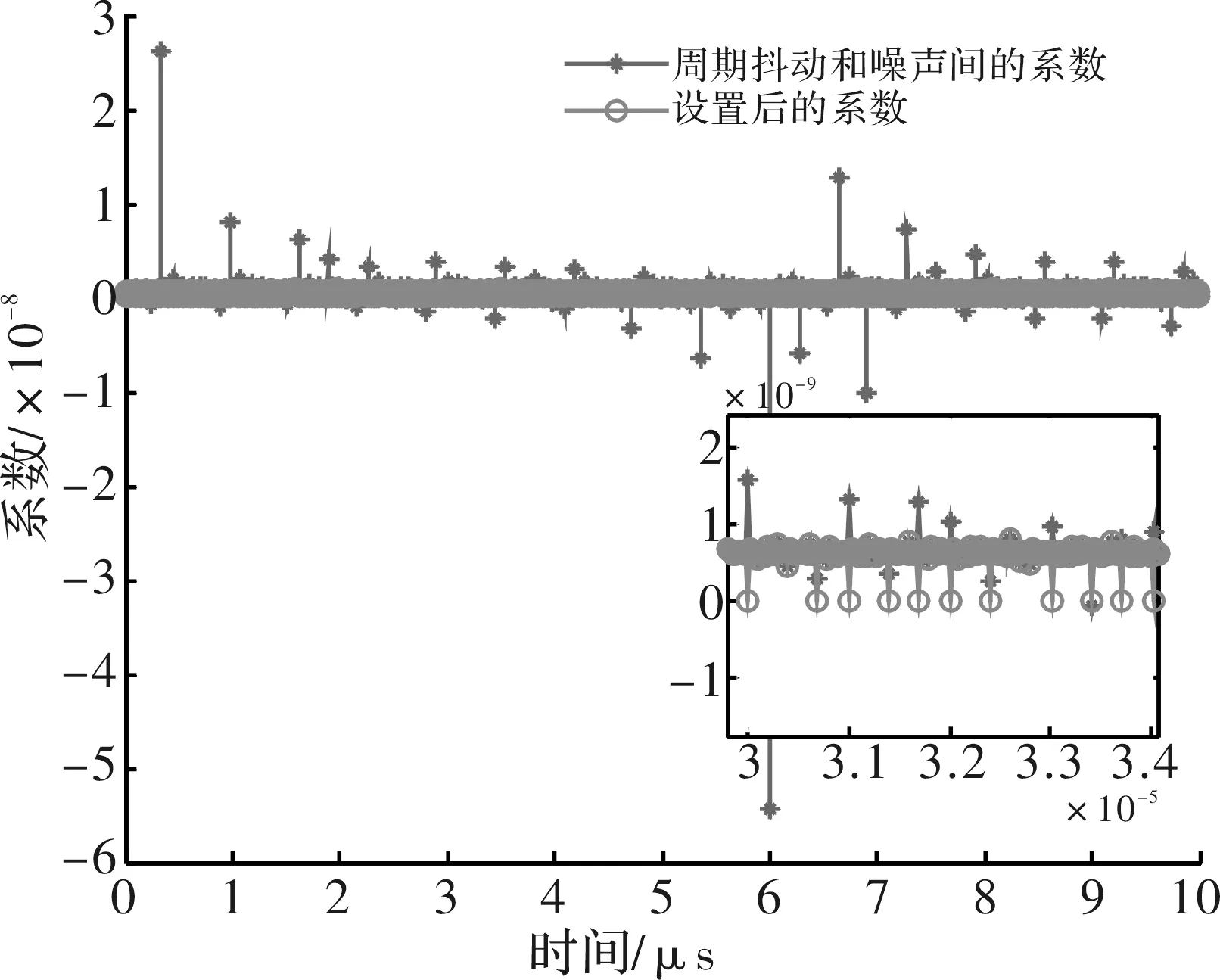
图8　周期抖动和电源噪声的比值系数

系数K能应用于预测不同电源噪声下的周期抖动。当电源噪声是由不同频率的正弦波累加所成时，周期抖动计算公式如下

(7)

其中，n是具有不同频率的电源噪声数量；fi表示不同电源噪声的频率；Tvco表示压控振荡器的振荡周期；k表示一个常系数；m表示不同电源噪声频率fi的最小公倍数与Tvco的比值；φ表示电源噪声和压控振荡器输出信号的相位差；Ai表示电源噪声的振幅。

将式(7)代入式(6)，得到抖动峰峰值。表2中显示了将通过式(6)和式(7)得到的抖动峰峰值与通过HSPICE仿真得到的抖动峰峰值的对比，其中Vpp是正弦电压噪声的峰峰值，表中的数据说明了式(7)的正确性。

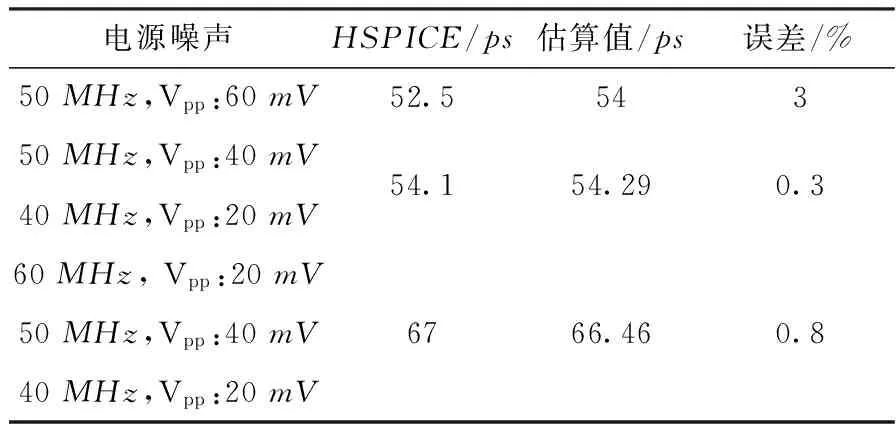
表2　HSPICE仿真抖动峰峰值和用本文方法结果的对比

4结束语

抖动是衡量锁相环性能的重要参数，在高速电路设计中对抖动的研究变得越来越重要，特别是抖动和电源噪声之间的线性关系。本文通过公式推导得到用周期抖动表示相位抖动的公式。通过分析锁相环输出信号与周期抖动可知周期抖动和电源噪声具有良好的线性关系，并不受压控振荡器控制电压波动的影响。周期抖动和电源噪声近似的线性关系可以用来准确预测锁相环输出信号的抖动峰峰值。通过对比HSPICE仿真和本文计算的抖动峰峰值，说明了文中方法的有效性。

参考文献

[1]魏建军.快速锁定的低功耗电荷泵锁相环[J].华南理工大学学报,2009,37(9):71-76.

[2]王照峰,王仕成,苏德伦.锁相环电路的基本概念及应用研究[J].电气应用,2005,24(8):46-48.

[3]陈文焕.电荷泵锁相环的基础研究[D].成都:电子科技大学,2005.

[4]鲁昆生,王福昌.电荷泵锁相环设计方法研究[J].华中理工大学学报,2000, 28(1):62-64.

[5]EricBogatin.信号完整性与电源完整性分析电源完整性分析[M].2版.李玉山,刘洋,译.北京:电子工业出版社,2015.

[6]贝斯特.锁相环设计、仿真与应用[M].5版.北京:清华大学出版社,2007.

[7]Synopsys.HSPICE®Simulationandanalysisuserguide[M].Ameria:Synopsys,2007.

[8]姚婧婧,赵红东,毛键,等.锁相环电路中压控振荡器的分析与设计[J].电子设计工程,2011,19(24):177-180.

[9]房庆艳.压控振荡器的设计与优化[D].哈尔滨:哈尔滨工程大学,2009.

[10]李鹏.高速系统设计:抖动、噪声与信号完整性[M].李玉山,译.北京:电子工业出版社,2009.

Analysis of Period Jitter Induced by Power Supply Noise of Phase Locked Loop

ZHUJian

(SchoolofElectronicEngineering,XidianUniversity,Xi’an710071,China)

AbstractIn terms of the jitter in phase locked phase loop caused by the power supply noise, the equation used to predict the peak-to-peak jitter induced by power supply noise is presented through analyzing the relation between the power supply noise, the phase jitter and the period jitter. The maximum error between the results predicted by the equation presented in this paper and simulated by HSPICE is 3%, which verifies the accuracy of this equation.

Keywordsphase clocked loop; power supply noise; period jitter

收稿日期:2015- 11- 13

作者简介:朱剑(1990-),男,硕士研究生。研究方向：电源完整性等。

doi:10.16180/j.cnki.issn1007-7820.2016.07.030

中图分类号TN911.8

文献标识码A

文章编号1007-7820(2016)07-102-04