基于萤火虫算法的变步长语音信号盲源分离
栾先冬,徐 岩
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
基于萤火虫算法的变步长语音信号盲源分离
栾先冬,徐岩
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
摘要针对传统的自然梯度算法对语音信号进行盲源分离时,算法存在收敛速度和稳态误差的矛盾。文中提出一种新的变步长自然梯度算法,利用荧火虫算法对自然梯度算法的步长调整,使算法的步长随信号的分离度变化,并通过计算机仿真验证了该算法的有效性,算法的分离效果更好,收敛速度更快,且稳态误差更小。
关键词萤火虫算法;变步长;盲源分离
盲源分离[1-2]是指在不知道源信号和混合方式条件下,根据源信号的统计特性从观测信号中恢复出源信号的过程。最典型的例子就是鸡尾酒会[3]问题。作为当今信息处理领域中研究的热点,随着其理论和技术的不断发展和成熟,已在语音信号分离与识别[4]、图像处理与识别[5]、生物医学信号处理[6-7]等领域有着广泛应用。
独立成分分析[8](Independent Compo-nent Analysis,ICA)作为盲源分离的一种主要方法,先假设源信号间相互独立,再对观测信号进行某种非线性变换,使各输出信号间尽可能的相互独立。目前ICA中有许多有效的算法,如扩展Infomax算法[9],FastICA[10],自然梯度算法[11]等。其中以自然梯度算法最为著名。
Amari在随机梯度算法的基础上,从黎曼空间的角度出发,提出了自然梯度算法[12]。事实上,自然梯度算法的稳定性更强,分离效果更好。学习步长和非线性函数的选取影响自然梯度算法的性能,因此选择一个理想的步长是关键。当传统的自然梯度算法对语音信号盲分离时,步长通常被设定为一个固定常量,设定过大虽然收敛速度快,但影响算法的稳定性,甚至不能收敛;过小虽增加一定的稳定性,但收敛速度慢,不能满足人们的要求。本文提出了一种基于萤火虫算法的变步长自然梯度算法,通过用萤火虫算法去优化自然梯度算法中的步长,使选择的步长不断变化且达到信号的最大分离度,从而更快、更好地分离观测信号。
1盲源分离问题
1.1盲源分离的基本模型
盲源分离问题的一般模型如图1所示。

图1盲源分离框图
S(
t
)=[S
1
(
t
),S
2
(
t
),…S
n
(
t
)]
T
为
n
个语音源信号,X(
t
)=[X
1
(
t
),X
2
(
t
),…X
n
(
t
)]
T
为
n
个传感器接受到的观测信号,忽略噪声和传输延迟的影响,即线性瞬时无噪声混合模型。则观测信号与源信号之间的关系为
X(t)=AS(t)
(1)
式中,A是一个n×n的非奇异矩阵,模拟传输信道的参数。盲源分离问题的实质就是在混合矩阵A和源信号St未知的情况下估计分离矩阵W,使X(t)通过W后输出各分量尽可能相互独立的Y(t)即
Y(t)=WX(t)=WAS(t)
(2)
输出的Y(t)为源信号S(t)的估计。
1.2自然梯度算法
能否找到最佳的分离矩阵W是盲源分离问题的关键。为此人们用互信息最小化、最大似然估计法、信息极大化等许多不同的方法求得最优解。依据自然梯度算法的定义,所有方法可总结为相同的迭代表达式
Wk+1=Wk+u(I-φ(Y)YT)Wk
(3)
式中,k为迭代次数;Wk为k次的分离矩阵;u为步长(学习率);I为单位矩阵;φ(Y)为非线性函数,与源信号的概率密度有关,不同的信号分布采用不同的非线性函数,由于所研究的算法针对语音信号的盲源分离,绝大数语音信号服从亚高斯分布,因此本文采用 。
2萤火虫算法
剑桥学者Yang在2009年提出萤火虫算法[13-14](Firefly Algorithm,FA),是模拟自然界中萤火虫发光行为的随机优化算法。利用其发光特性和趋光特性向亮度更高的位置移动,进而找到最大亮度的萤火虫位置。与遗传算法和粒子群算法相比,萤火虫算法具有使用简单、鲁棒性强、易于实现等特点,收敛速度更快、搜索全局最优解的能力更强且不易于陷入局部极值,从而使寻优结果更准确。目前已被应用到装配序列规划问题[15]、图像分割处理[16]等方面。
亮度和吸引度是萤火虫算法的两个重要参数。亮度体现了萤火虫所处位置的优劣并决定其移动方向;萤火虫移动的距离则由吸引度决定。不断地更新亮度和吸引度使被优化的目标达到最佳位置。
萤火虫的相对荧光亮度为
I=I0×e-γrij
(4)
其中,I0为萤火虫的自身最大荧光亮度(r=0 ),其大小取决于目标函数,目标函数值越大其自身亮度就越亮;γ为光强吸收系数,传播介质的吸收和萤火虫个体间距离的增加使荧光逐渐减弱,rij为萤火虫个体i和j之间的空间距离。
萤火虫的吸引度为
(5)
其中,β0为最大吸引度,即萤火虫间距离为零时的吸引度。被吸引后,萤火虫i根据式(6)向荧火虫j移动,更新自身的位置
Xi=Xi+β×(Xj-Xi)+α×(rand-0.5)
(6)
其中,Xi,Xj为萤火虫i和j所处空间的位置;α为步长因子,是[0,1]上的常数;rand为[0,1]上服从均匀分布的随机因子。萤火虫移动的距离主要由吸引度的大小决定。亮度高的萤火虫向亮度低的萤火虫移动。在萤火虫位置的更新过程中加入扰动项α×(rand-0.5)可扩大搜索区域,防止过早陷入局部极值点。所有萤火虫个体在经过多次的扰动后都聚集在亮度最高的萤火虫的位置上,从而找到最优解。
3变步长自然梯度算法
3.1目标函数的选取
取

(7)
式中, ‖·‖为Frobenius范数;ΔWk定性上表示的是信号的分离的状态:若信号的分离状态差,则ΔWk值越大;反之ΔWk值越小。当ΔWk=0时,信号得到完全分离。由式(7)可知信号的分离状态与步长u的大小有关。因此,可通过对ΔWk的控制选择合适的u。
3.2算法原理
初始化萤火虫个体的个数及位置,个数表示步长参数的数量;位置表示所选步长参数的大小。将ΔWk作为萤火虫算法的目标函数,通过最小化这个目标函数使得经过数次迭代后算法返回的值是亮度最大的萤火虫的位置,即达到最大分离度时的步长。
3.3算法步骤
(1)对观测信号白化和去均值处理。可减小计算量,提高算法精度;(2)初始萤火虫算法参数。萤火虫个体初始位置、萤火虫的个体数量M、最大吸引度β0、步长因子α、光强吸收系数γ、最大迭代次数T;(3)计算萤火虫的亮度并排序。计算每个萤火虫对应的ΔWk,将其值视为其亮度,排序后得到亮度最大的萤火虫位置;(4)判断迭代是否结束。判断迭代次数是否到达到最大迭代次数T,达到则转步骤(5),否则转(6);(5)输出亮度最大的萤火虫位置及其亮度,将得到的最大亮度的位置作为自然梯度算法的步长,对语音信号进行分离;(6)更新萤火虫位置。对已在最优位置的萤火虫进行一次随机扰动,故搜索次数加一次,转步骤(3)进行下一次移动。
4仿真实验及性能分析
4.1仿真实验
选取3路纯净的语音信号S1,S2,S3作为源信号来验证算法的可行性。计算机仿真后得到图2所示。再随机产生一个 阶的混合矩阵 ,与语音源混合后变成三路混合信号X1,X2和X3。仿真结果如图3所示。
选取固定步长为u=0.000 1;萤火虫个数M=50;萤火虫的初始位置U=0.000 5×rand(1,50);最大吸引度β0=1.0;光强吸收系数γ=1.0;步长因子α=0.000 2;最大迭代次数T=100。使用传统固定步长自然梯度算法和本文所提出的基于萤火虫算法的变步长自然梯度算法分别对混合信号进行分离,两种算法各自最大的迭代次数为300;初始化分离矩阵W=0.1×eye(3,3);计算机仿真的分离结果如图4和图5所示。

图2 语音源信号
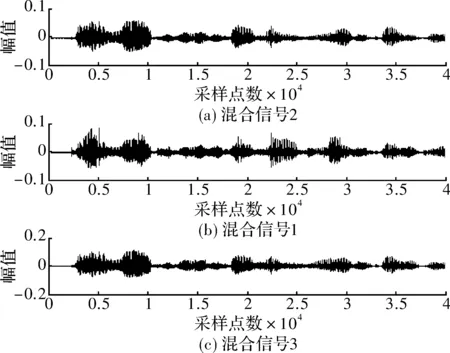
图3 混合信号
4.2性能分析
通过观察两种算法分离后得到的分离信号,如图4和图5所示,两种算法都能有效地分离出信号。由于ICA算法存在分离顺序和幅度的不确定性,因此暂时不考虑这两个因素。用萤火虫算法改进的变步长自然梯度算法得到的分离信号相比于固定步长的自然梯度算法更加接近原始语音信号。
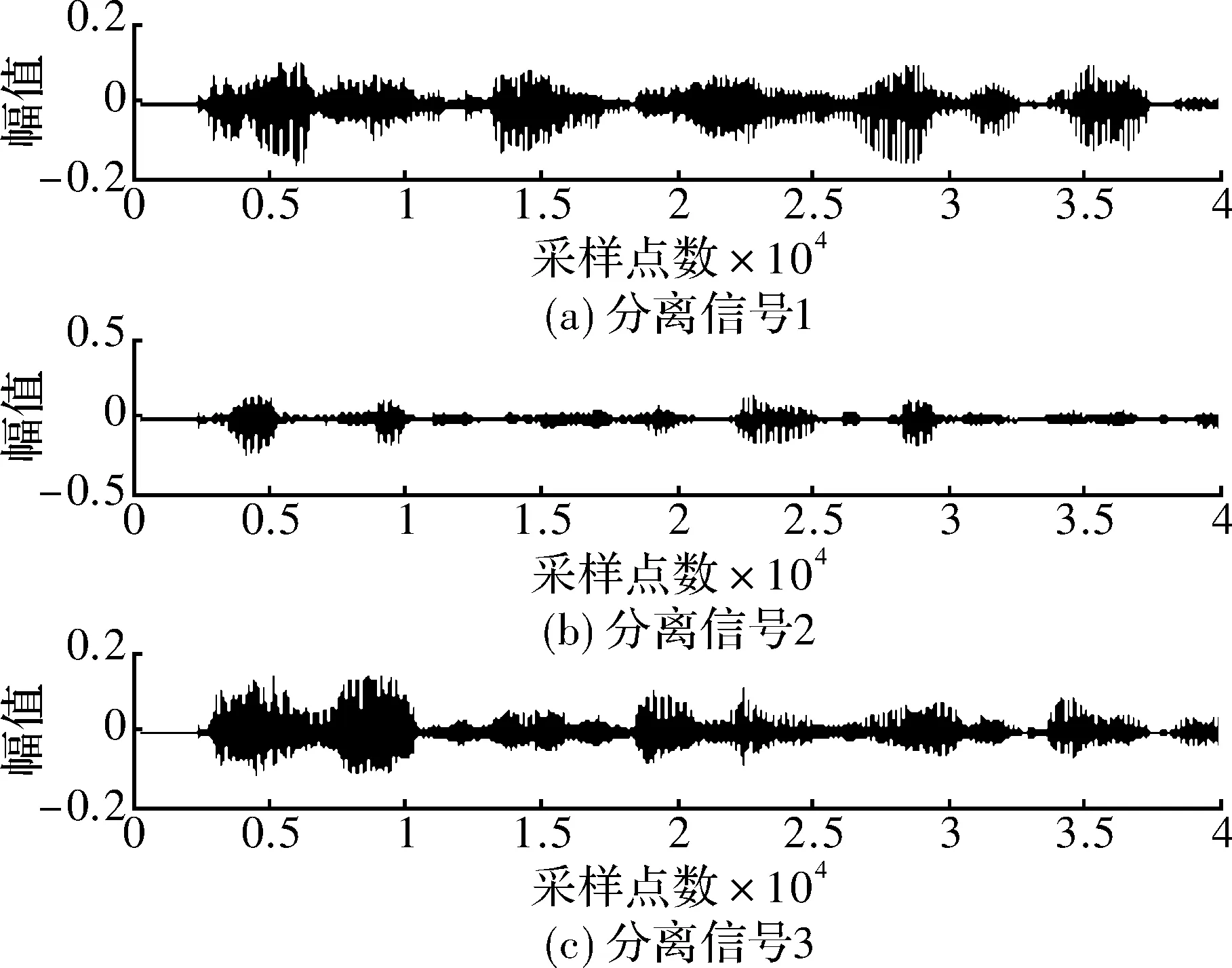
图4 固定步长分离信号
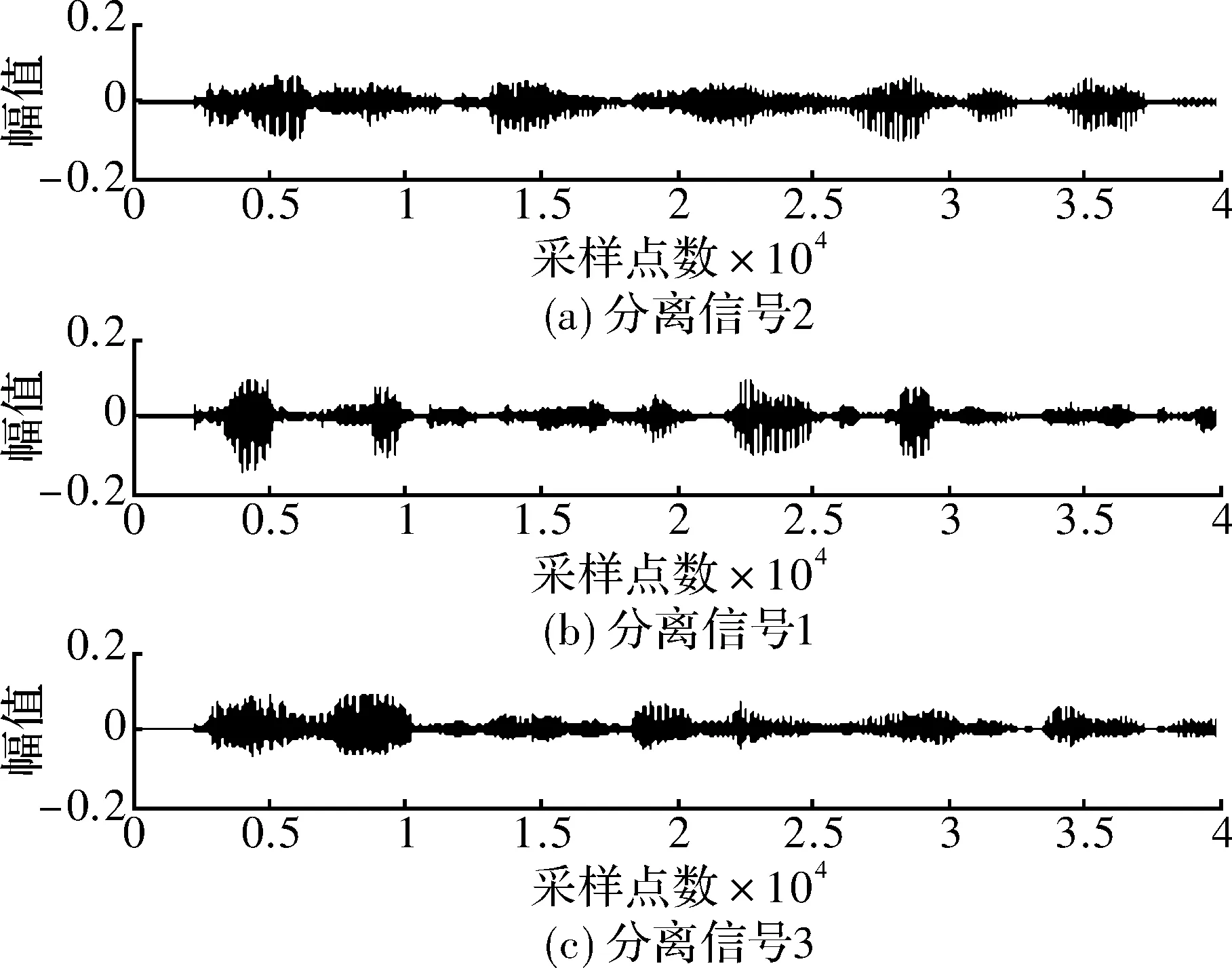
图5 萤火虫算法改进分离信号
通过具体的评价指标分析:本文选用分离后输出信号的串音误差E[17]来量化分离算法的性能。串音误差
(8)
式中,Pij为全局矩阵G的元素;G=W×A;maxk|Pij|表示G的第k行或列元素绝对值中的最大值。当信号得以精确分离时,理论上 的值应该为零,但实际上一般为较小的值。
通过仿真得到两种算法的串音误差E如图6所示。

图6 串音误差曲线图
两种算法独立运行30次,得到两种自然梯度算法达到收敛时的平均串音误差和平均迭代次数的结果如表1所示。

表1 两种自然梯度算法的性能比较
从两种算法的串音误差E可看出,本文提出基于萤火虫算法的变步长自然梯度算法与传统的固定步长的自然梯度相比,有更快的收敛速度和更小的串音误差,说明改进后的算法在语音信号的分离性能优于传统的自然梯度算法。
5结束语
本文提出了基于萤火虫算法的变步长自然梯度算法,与传统的固定步长自然梯度相比,该算法具有更理想的收敛速度和稳态误差,有效地解决了收敛速度和稳态误差的矛盾。理论分析和实验结果都表明该算法优于传统的固定步长自然梯度算法。由于本文所使用的是最基本的萤火虫算法,下一步可通过对其进行改进,进而优化算法性能,取得更好的效果。
参考文献
[1]Herault J,Jutten C.Blind separation of sources,Part I:an adaptive algorithm based on neuromimetic architecture[J].Signal Processing,1991,24(1):1-10.
[2]Pham D T.Blind separation of instantane-ous mixture of sources via an independent component analysis[J].IEEE Transations on Signal Prosessing,1996,44(11):2768-2779.
[3]Haykin S,Chen Z.The cocktail party problem[J].Neural Computation,2011,17(9):1875-1902.
[4]Choi C H,Chang W,Lee S Y.Blind source separation of speech and music signals using harmonic frequency depedent independent vector analysis[J].Elecronic Letters,2012,48(2):124-125.
[5]刘琚,张新刚,孙建德.一种基于ICA的图像水印方法[J].电路与系统学报,2003,8(3):55-59.
[6]马明,邹志斌,杨玉林,等.采用盲源提取和后小波滤波的胎儿心电图提取[J].仪器仪表学报,2010, 31(5):1096-1101.
[7]Hesse C W,James C J.On semiblind source separation using spatial constrains with applications in EEG analysis[J].IEEE Transations on Biomedical Engineering,2006,53(12):2525-2534.
[8]Lee T W,Girolami M,Sejnowski T J.Independent compontment analysis using an extended informax algorithm for mixed sub-Gaussian and super-Gaussian sources[J].Neural Computation,1999,11(1):417-441.
[9]马守科,何选森,许广廷.基于扩展Informax算法的变步长在线盲分离[J].系统仿真学报,2007,19(19):4513-4516.
[10] Hyvarinen A,Oja E.A fast fixed point al-gorithm for independent component analysis[J].Neural Computation,1997,9(7):1483-1492.
[11] 马建仓,冯冰,程存虎,等.自然梯度盲分离算法在振动信号处理中的应用[J].火力与指挥控制,2011,36(4):154-157.
[12] Amari S.Natural gradient works efficiently in learning[J].Neural Computation,1998,10(2):251-276.
[13] 刘长平,叶春明.一种新颖的仿生群智能优化算法:萤火虫算法[J].计算机应用研究,2011,28(9):3295-3297.
[14] Yang X S H.Firefly algorithms for mul-timodal optimization[C].CA,USA:In Stochastic Algorithms:Foundations and Applications,Lecture Notes in Computer Science,2009.
[15] 曾冰,李明富,张翼.基于改进萤火虫算法的装配序列规划方法[J].计算机集成制造系统,2014,20(4):799-806.
[16] 陈恺,陈芳,戴敏,等.基于萤火虫算法的二维熵多阈值快速图像分割[J].光学精密工程,2014,22(2):517-523.
[17] 李宗,冯志鹏,褚福磊.基于改进的串音误差的盲分离评价指标[J].振动与冲击,2012,31(18):85-88.
Variable Step-size Blind Sources Separation for Speech Sig-nals by Firefly Algorithm
LUAN Xiandong, XU Yan
(School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
AbstractTraditional natural gradient algorithm of blind source separation for speech signals is contradictions, which suffers errors between convergence speed and steady-state. A novel variable step-size algorithm is proposed to solve this problem. The step-size of traditional natural gradient algorithm is adjusted by the firefly algorithm to yield variable signals with the separation degree. Computer simulations verify the feasibility of this new algorithm, which offers better separation results with faster convergence and less steady-state errors.
Keywordsfirefly algorithm; variable step-size; blind source separation
收稿日期:2015- 11- 16
基金项目:国家自然科学基金资助项目(61461024)
作者简介:栾先冬(1991-),男,硕士研究生。研究方向:语音信号增强等。徐岩(1963-),男,教授。研究方向:盲信号处理等。
doi:10.16180/j.cnki.issn1007-7820.2016.07.002
中图分类号TN912.35
文献标识码A
文章编号1007-7820(2016)07-004-04

