基于dq变换的锁相环设计与仿真
何 攀, 席自强
(湖北工业大学 太阳能高效利用湖北省协同创新中心, 湖北 武汉 430068)
基于dq变换的锁相环设计与仿真
何 攀, 席自强
(湖北工业大学 太阳能高效利用湖北省协同创新中心, 湖北 武汉 430068)
针对一般锁相环在电网电压波动时存在锁相误差的问题,提出了一种基于dq变换的锁相环新方案,并对锁相环参数进行了整定。对于电网电压频率变化、相位变化以及谐波注入的影响,利用matlab进行了仿真分析。仿真结果表明,新方案有很好的跟踪效果,跟踪速度快,精度高,能较好实现相位锁定。
电压波动; dq变换; 锁相环
新能源技术的不断发展,使得越来越多的分布式电源接入电网中,能精确快速锁定电网电压的相位,对于需要并网运行的设备也变得越来越重要。锁相主要分为硬件锁相和软件锁相两种,由于硬件锁相精确度不高,容易受到干扰,所以现在广泛采用软件锁相技术,数字处理器的大规模发展,也使得软件锁相技术更易于实现[1-4]。
传统的锁相环采用过零锁相的方法,但在电压存在畸变的情况下,锁相效果不太理想;电压不平衡的状态下,可以通过傅里叶变换将基波成分和谐波成分分别提取出来,但必须采集完整的周期数据,不能实时计算[5-7]。
因此,本文根据坐标变换的原理[8],建立了三相电网电压在同步旋转坐标系下的系统模型,详细阐述了锁相环的结构及原理。并通过仿真验证了锁相环在电压波动时的跟踪效果。
1 算法模型
在三相电网电压平衡的情况下,三相电网电压全部为正序分量,其在abc坐标系下的表达式如下:
(1)
其中,Um为各相电压幅值,ω为电网电压角频率,φ为初始相角。
利用Clark变换,将式(1)中三相电压变换到两相静止αβ坐标系:
再利用Park变换,最终转换为dq坐标系下的直流分量Ud、Uq:
1.1同步坐标系锁相环原理
根据瞬时无功功率理论,将三相电压合成矢量在同步坐标系下进行分解,图1所示为同步旋转坐标系示意图,图中Us为三相电压合成矢量,与坐标轴的夹角为θ(θ=ωt),θ′为锁相环实际输出电压矢量与坐标轴的夹角,Ud、Uq分别为三相合成矢量在同步旋转坐标系下的d轴和q轴上的直流分量。
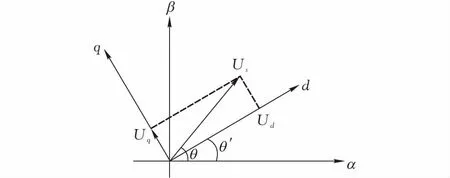
图 1 同步旋转坐标系向量图
此时对应的d轴和q轴上的直流分量Ud、Uq分别为:
通过输出电压角度的控制,使锁相输出电压U0逐渐接近电网电压Us,即可完成锁相,此时相位满足θ=θ′。三相电压经过dq变换后,正序分量的阶次降低为直流分量,负序分量阶次在原有基础上增加,通过设置合理的低通滤波器,使得直流分量通过,而负序分量和谐波得以滤除。从而在一定程度上,可以抑制负序分量和谐波对锁相环造成的影响。
1.2锁相环结构设计
由图2可以看出,锁相环的控制系统主要由一个低通滤波器、一个PI控制器和一个积分器组成。
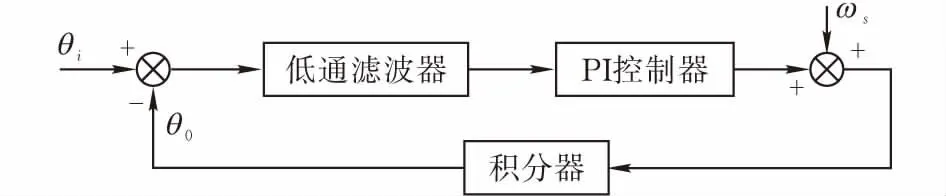
图 2 锁相环基本结构
当相位差较小时,sin (θ-θ′)可以近似等效为θ-θ′。因此,输入信号可由θi近似代替,输出信号为θ0。
三相电压Ua、Ub、Uc经过坐标变换后得到直流分量Ud、Uq,当锁相成功时,Uq值为0,若Uq值存在误差,则将Uq与参考值0比较,再将产生的误差信号经过PI调节器得到ωerr,再通过与电网理论角频率相加,并经过积分器得到相位θ,该相位即为坐标变换所需要的三角函数相位值。最终可以实现整个锁相环的闭环控制。实现过程如图3所示。

图 3 锁相环原理图
由图3可以得到,在理想条件下,系统的开环传递函数
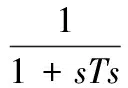
(2)
系统闭环传递函数
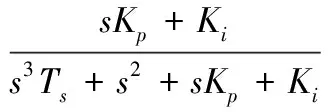
(3)
式(2)和(3)中,Kp为比例系数,Ki为积分系数,Ts为由于采样延迟而产生的等效惯性时间常数。通过合理选择各控制器的参数,综合考虑系统抗干扰能力、跟踪速度和稳定性的要求,可以使系统达到较好的平衡。
2 仿真分析
为了验证所提出的锁相环功能,在Matlab中搭建了锁相环的仿真模型,仿真采用的三相电网电压为380 V/50 Hz的理想电压源。
对于电压波动对锁相环造成的影响,分别设计了不同的电压波动情况,并对各种情况下的锁相环性能进行了测试。
如图4所示,在A相电压Ua初始相位为60°时,锁相环输出电压U0在两个周期后能准确锁定A相电压。如图5所示,在A相电压Ua初始相位为180°时,即与正常电压相位相反时,能在不到两个周期的时间内锁定A相电压。由此可以得出在三相电压平衡时,对于任意相位,锁相环均可有效锁定。
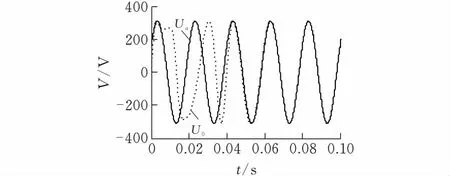
图 4 A相初始相位60°
如图6所示,此时电压Ua中含有30%的直流分量,频率不变。经过约两个周期的时间后,锁相环输出电压U0仍能准确跟踪Ua相位。

图 6 电压中含有直流分量
如图7所示,此时电压Ua中含有10%的5次谐波和20%的7次谐波,频率不变。在经过约两个半周期的时间后,锁相环最终成功锁定Ua相位。

图 7 电压中含有谐波分量
如图8所示,在系统运行至0.2 s时,电压Ua由50 Hz突变至150 Hz,幅值不变。经过0.04 s后,锁相环最终成功锁定Ua相位。可见系统能很好的应用于需要改变频率的变频场合。

图 8 频率突变
3 结论
本文对锁相环的基本原理进行了分析后,设计了锁相环的结构,并对所提出的锁相环进行了建模仿真。仿真结果表明,在三相电压平衡的条件下,锁相环能准确跟踪目标电压,并且不会受到初始相位的影响;在三相电压不平衡时,对于含有直流分量和谐波分量的情况,锁相环也能成功锁定相位,但会对锁相环跟踪性能造成影响,跟踪运行时间变长;在频率突变的情况下,锁相环也表现出良好的跟踪性能。
综上所述,本文提出的锁相环在电压存在相位变换、直流分量、谐波分量以及频率突变等情况下,均能准确跟踪目标电压,抗干扰能力强,能较好应用于并网条件恶劣的环境中。
[1] 王颢雄,马伟明,肖飞,等.双 d-q变换软件锁相环的数学模型研究[J]. 电工技术学报, 2011, 26(7): 237-241.
[2] 陈明亮,肖飞,刘勇,等. 一种正负序分离锁相环及其在并网型风力发电系统中的应用[J].电工技术学报,2011,28(8):181-186.
[3] Carugati I, Maestri S, Donato P G, et al. Variable sampling period filter PLL for distorted three-phase systems[J].IEEE Transactions on Power Electronics,2012,27(1):321-330.
[4] 刘海春,徐立智,谢少军.一种新的过零锁相方法[J].电力系统保护与控制,2010,38(19):147-150.
[5] 杜雄,刘延东,孙鹏菊,等.消除直流分量影响的并网变流器同步参考坐标系锁相环方法[J].电工技术学报,2013,28(12):24-31.
[6] 胡应占,郭素娜.适用于电网不平衡时的广义积分器锁相环设计[J].电力系统保护与控制,2014,42(11):148-154.
[7] Karimi-Ghartemani M. Linear, pseudolinear enhanced phased-locked loop (EPLL) structures [J]. IEEE Transactions on Industrial Electronics,2014,61(3):1464-1474.
[8] 洪小圆,吕征宇.基于同步参考坐标系的三相数字锁相环[J].电工技术学报,2012,27(11):203-210.
[责任编校:张岩芳]
DesignandSimulationofPhase-lockedLoopBasedondqTransform
HE Pan, XI Ziqiang
(HubeiCollaborativeInnovationCenterforHigh-efficiencyUtilizationofSolarEnergy,HubeiUniv.ofTech.,Wuhan430068,China)
Aiming at the problem of phase-locked error in the voltage fluctuation of the general phase-locked loop, a new scheme of phase-locked loop based on dq transform is proposed, and the parameters of phase-locked loop are set. For the voltage frequency conversion, phase change and the effect of harmonic injection, the simulation analysis is carried out by using matlab.The simulation results show that, the proposed phase-locked loop has good tracking performance, fast tracking speed and high precision, and can realise phase locking.
voltage fluctuation; dq transform; phase-locked loop
2016-08-15
何 攀(1991-), 男, 湖北仙桃人,湖北工业大学硕士研究生,研究方向为电力系统及其自动化
席自强(1960-),男,湖南东安人,工学博士,湖北工业大学教授,研究方向为电力系统及其自动化
1003-4684(2017)05-0093-03
TM464
A

