基于反正弦函数加速收敛的新型有源滤波器锁相环
李泓霖 郑 征
基于反正弦函数加速收敛的新型有源滤波器锁相环
李泓霖1,2郑 征1
(1.河南理工大学电气工程与自动化学院,河南 焦作 454000;2.华能沁北发电有限责任公司,河南 济源 459001)
为保证指定次谐波补偿有源滤波器(Active Power Filter,APF)取得更好的补偿效果,主要研究了有源滤波器的锁相环(Phase Locked Loop,PLL)技术。本文根据dq变换原理,提出了一种基于反正弦函数加速收敛的新型有源滤波器锁相环技术。该技术在误差范围内,可实现绝大部分相位偏移范围内的1次调节锁相。与传统的基于dq变换的锁相环技术相比,新型锁相环技术具有明显的速度优势和灵活性。最后,仿真与实验结果验证了上述分析的正确性。
有源滤波器;锁相环;反正弦函数;加速收敛
1 研究背景
随着工业的发展,大功率非线性负载在工业中被广泛应用,由非线性负载产生的谐波会引起电压、电流波形畸变、电气设备的共振和干扰、过早老化等问题。最常用于治理电流型谐波源的并联型有源电力滤波器,由于安装方便、补偿效果好、易于保持系统稳定等,成为电力电子技术领域的研究热点。
近年来,关于APF指定次补偿的研究多集中于谐波的提取方法与系统控制方法等方面,而对于锁相环技术的研究还有待加强。锁相环技术是整个APF补偿谐波的基础,锁相环响应速度的快慢直接影响APF的补偿效果。章梁磊[1]提出了一种单相软锁相环技术,但未对三相锁相环进行研究;黄颖姝、陈永强和俞博[2]等提出了一种过零锁相法,但不能解决电压畸变时锁相困难的问题;李林才和陈艳峰[3]在dq变换的基础上提出了一种动态计算锁相环PI参数的锁相环技术,但动态响应较慢、运算量较大;吉正华、韦芬卿和杨海英[4]对传统dq变换锁相环进行了改进,调整了滤波环节位置、取消了前向积分环节,使锁相环在动态相位跟踪及不平衡电压检测等方面的性能得到显著改善。
本文根据传统dq变换锁相环的原理,提出了一种基于反正弦函数加速收敛的新型锁相环技术。该锁相环技术运用查表的方法,将q轴分量先经反正弦处理再加权后作为p分量参与PI调节,此法可加快PI调节的收敛速度。与传统锁相环相比,新型锁相环具有更好的快速性与灵活性。最后,仿真与实验结果验证了上述分析的正确性。
2 APF指定次谐波补偿
2.1 APF指定次谐波补偿的基本原理
APF系统主要由两大方面组成:一方面是由电网电压和非线性负载组成的谐波源系统,其中由于非线性负载的存在,系统中产生大量的谐波电流;另一方面由谐波控制部分和谐波产生部分组成的谐波补偿系统,即有源滤波器。
APF指定次谐波补偿的基本原理是APF通过检测负载的某次谐波电流ir,并发出与负载某次谐波幅值相等、相位相反的电流ic,二者相互叠加,相互抵消。
2.2 指定次谐波的检测与控制
2.2.1 指定次谐波的检测。谐波电流的检测直接影响APF的补偿性能,主要检测方法有:基于离散傅立叶变换的检测方法、基于瞬时无功理论的检测方法和基于神经网络的检测算法等。本文在瞬时无功理论的基础上采用基于多同步旋转坐标变换的指定次谐波提取方法。
基于多同步旋转坐标变换的指定次谐波提取方法的原理是:首先检测三相负载电流,然后在三相静止坐标系下通过n次谐波同步旋转坐标变换使三相负载电流变换到n次谐波坐标系下,最后通过低通滤波器滤除交流部分,得到n次谐波在n次谐波坐标系下的d轴直流分量和q轴直流分量(注:θ为A相电网电压锁相环角度,n为指定次谐波次数)。n次谐波正序、负序变换公式分别如式(1)、式(2)所示:

现在以提取5次谐波电流为例,详细阐述指定次谐波多同步旋转坐标提取法。首先检测负载电流,然后通过5次谐波旋转坐标变换,使负载电流变换到5次谐波旋转坐标下,由于5次谐波电流为负序谐波,因此变换公式使用式(2),其中n=5。此时,在5次谐波旋转坐标下,除5次谐波直流量外,还有另外的谐波电流交流量,然后通过低通滤波器滤除交流谐波得到5次谐波电流的直流信息,即5次谐波电流的提取已经完成。其他次谐波电流的提取与之相类似,但要注意,6k+1次谐波为正序谐波,6k-1次谐波为负序谐波,其中k=1,2,3……。
以上坐标变换都是在指定次谐波坐标系下完成的,为统一控制,需要将n次谐波坐标下的直流量通过n次谐波坐标反变换转换到基波坐标下。n次谐波坐标反变换的正序、负序变换公式分别如式(3)、式(4)所示。

2.2.2.指定次谐波补偿的控制方法。APF的控制方法众多,常规的PI控制器控制简单,并能对直流恒定信号无静差地跟踪。但APF的参考电流是多个频率叠加的周期性信号,传统PI控制无法直接对参考电流做到无差跟踪。
对此,对传统PI控制进行了改进,采用基于PI调节的指定次谐波无静差控制。首先,使负载电流ir与APF补偿电流ic做差,其差值相当于系统电流;其次,将差值电流通过与指定次谐波同步的旋转坐标变换转化到dq坐标下,再通过低通滤波器求得指定次谐波在dq坐标下的直流分量;最后,对该直流分量进行PI调节。
电网电压通过PLL求得的角度θ是整个APF控制算法的基础。此角度不仅参与基波坐标系下的坐标变换,而且也参与谐波坐标系下的坐标变换,因此,求得锁相环角度的优劣直接影响APF的补偿效果。本文将传统的基于dq坐标变换锁相环技术与新型锁相环技术相比较,证明该技术的优越性。
3 基于dq变换的锁相环技术
基于dq变换的锁相环首先将三相电网电压做Clark、Park变换,得到两相旋转坐标系下的Ud与Uq两个直流分量,其中,θ为锁相环输出相位。
Clark、Park变换公式分别如式(5)、式(6)所示:

由式(5)、式(6)可计算得:
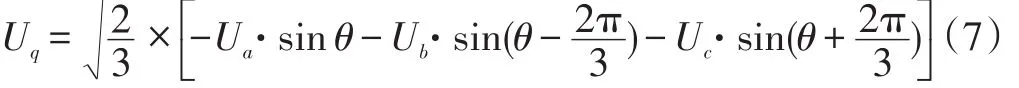
由式(7)可得出直流分量Uq的最终形式。分析(7)式可得:当θ与Ua相位大小相同时,Uq=0;当Ua相位超前锁相环输出相位θ时,Uq>0;当Ua相位滞后锁相环输出相位θ时,Uq<0。由于Uq为直流分量,所以,可通过PI调节将Uq调节为0,从而实现锁相环的锁相。
现如今,通常所用的PI调节为线性调节,基本调整原理式如(8)所示:

其中,Δθ是软锁相环相位调整增量,k1、k2分别为PI调节器中P和I的比例系数。
此调节方法的优点是参与的运算都是线性运算,因此在DSP中较容易实现。但其也有缺点,当角度范围较大时,需调节多次才能使Uq为0,而每次调节都需要进行Clark变换和Park变换。因此,此方法运算量较大,影响锁相环的锁相速度。
4 新型锁相环技术
为解决传统基于dq变换的锁相技术中PI调节收敛速度慢的问题,本文提出了一种使用反正弦函数加快PI调节收敛的算法。
由式(7)可得式(9),其中θ0为Ua的相位:

由式(9)可知,在锁相环的调节过程中,实际需要的角度增量即为sin-1Uq。因此,在反正弦函数计算精度理想的情况下,将传统PI调节(8)式中的P分量改为sin-1Uq,k1取1,取消I调节量,则可实现1次调节收敛。式(10)为改进后的PI调节公式:

但在实际的工业控制应用过程中,锁相环的功能往往通过DSP等嵌入式处理器来进行计算和实现,而反正弦函数是无法在DSP等嵌入式处理器中进行直接计算的,因此,往往采用如查表法、泰勒展开、CORDIC算法等方法来实现,后两种方法计算的精度较高,但迭代次数过多且耗时过长,并不适用于锁相环中的反正弦计算;查表法则简单快捷。本文所做的仿真中反正弦的计算正式采用了查表法。
由于查表法具有一定的误差,在某些角度上,1次调整可能达不到精度要求,所以,在实际应用中,仍然采用PI调节,具体公式如式(11)所示:

5 仿真与实验分析
5.1 仿真验证分析
为验证上述分析的正确性,搭建了Smulink仿真模型,仿真所用的负载为电感滤波型三相全桥不控整流电路,APF只补偿负载电流中的5、7、11、13次谐波,系统仿真参数如表1所示。

表1 系统仿真主要参数
本文在相同电网电压与负载的前提下,将新型锁相环与传统基于dq变换的锁相环分别应用于有源滤波器指定次谐波补偿,并从补偿后的电网电流波形和谐波电流畸变率两方面进行对比。
5.2 补偿后的电网电流波形的对比
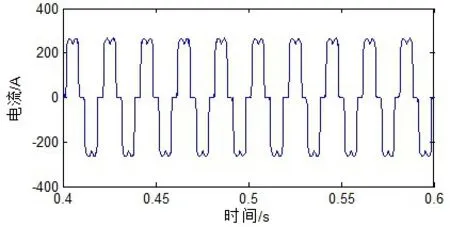
图1 APF补偿前的电网电流

图2 传统锁相环下APF补偿后的电网电流

图3 新型锁相环下APF补偿后的电网电流
图1 为APF补偿前的电网电流,图2为传统锁相环下APF补偿后的电网电流,图3为新型锁相环下APF补偿后的电网电流。对比图1与图2可知,当采用传统锁相环补偿电网谐波电流时,电网电流由于APF谐波补偿而趋于正弦,但依旧含有谐波含量;对比图2与图3可知,当采用新型锁相环补偿电网电流时,图3的波形比图2中的波形更趋于正弦,这证明:采用新型锁相环的有源滤波器具有更好的补偿效果,同时也说明新型锁相环具有较好的优越性。
5.3 电网电流谐波畸变率(THD)的对比
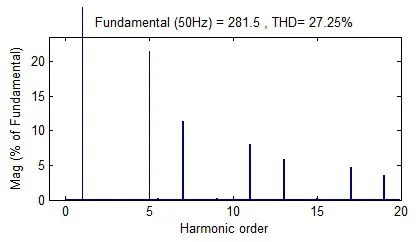
图4 APF补偿前的电网电流THD
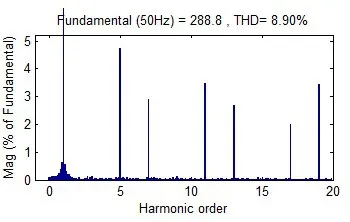
图5 传统锁相环下APF补偿后的电网电流THD

图6 新型锁相环下APF补偿后的电网电流THD
以上图4为APF补偿前的电网电流THD,图5为传统锁相环下APF补偿后的电网电流THD,图6为新型锁相环下APF补偿后的电网电流THD。对比图4与图5可知,当采用传统锁相环补偿电网谐波电流时,电网电流补偿后的THD值由27.25%下降为8.9%,即采用传统锁相环的APF也可补偿谐波电流;对比图4与图6可知,当采用新型锁相环补偿电网谐波电流时,电网电流补偿后的THD值由27.25%下降为6.26%;对比图5与图6可知,采用新型锁相环的APF具有更低的谐波畸变率,即证明采用新型锁相环的有源滤波器具有更好的补偿效果,同时也从侧面证明了(1)仿真的正确性。
6 结论
本文首先分析了有源滤波器指定次谐波补偿的基本原理、谐波提取方法和控制策略;然后对于控制策略中,锁相环的相位锁相分别从传统基于dq变换的锁相环和改进型的新型锁相环两方面出发,研究了基于反正弦函数加速收敛的新型锁相环优势;最后,搭建了有源滤波器指定次谐波补偿的仿真模型,分别比较了传统基于dq变换的锁相环和新型锁相环对于有源滤波器补偿效果的影响,分析表明:采用新型锁相环的有源滤波器具有更好的补偿效果,即证明了采用新型锁相环的优越性。
[1]章梁磊.一种单相软锁相环的改进算法研究[J].电子制作,2015(4):30-31.
[2]黄颖姝,陈永强,俞博,等.基于非线性PI控制器的三相锁相环实现[J].电气传动,2014(12):62-66.
[3]李林才,陈艳峰.基于PI调节的三相数字锁相环研究与实现[J].新技术新工艺,2012(2)65-69.
[4]吉正华,韦芬卿,杨海英.基于dq变换的三相软件锁相环设计[J].电力自动化备,2011(4):104-107.
New Active Power Filter Phase Locked Loop Based on Fast Convergence of Inverse Sine Function
Li Honglin1,2Zheng Zheng1
(1.College of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo Henan 454000;2.Huaneng Qinbei Power Generation Co.,Ltd.,Jiyuan Henan 459001)
In order to guarantee the compensation of APF Power Filter(APF),the PLL technology of ac⁃tive filter is studied.In this paper,based on the principle of dq transform,a new active filter phaselocked loop technique based on anti sinusoidal acceleration was proposed.In the range of error,this tech⁃nique can realize the 1 phase locking in most phase shift range.Compared with traditional PLL technology based on dq transform,the new PLL technology has obvious speed advantage and flexibility.Finally,simula⁃tion and experimental results verified the correctness of the above analysis.
APF;PLL;arcsin function;convergence acceleration
TM761
A
1003-5168(2017)10-0073-04
2017-09-01
河南省高等学校重点科研项目(17A470001);教育厅基础研究计划资助项目(15A470013)。
李泓霖(1988-),男,硕士,助理工程师,研究方向:电能质量、电力系统自动化等。

