带参数的五次Wang-Ball曲线的扩展*

张丹丹, 吴欢欢

(安徽广播电视大学 安庆分校，安徽 安庆 246001)



带参数的五次Wang-Ball曲线的扩展*

张丹丹, 吴欢欢

(安徽广播电视大学 安庆分校，安徽 安庆 246001)

摘要：定义了带3个形状参数α,β,γ的五次Wang-Ball型曲线；实现了五次Wang-Ball曲线到五次Said-Ball曲线及五次Bézier曲线的过渡，并具有五次Ball曲线的几何性质；分析了形状参数α,β,γ的几何意义，可对曲线的形状进行灵活的调整，并通过实例证明方法的有效性。

关键词：Wang-Bal曲线；Said-Ball曲线；Bézier曲线；形状参数；曲线设计

随着几何造型工业的发展，为了对曲线的形状进行调整，人们构造了Bézier曲线、B样条曲线、Ball曲线[1]。文献[2]介绍了两类新的Ball曲线，第一类介于Wang和Said曲线之间，第二类介于Bézier和Said曲线之间。文献[3]提出了三次Ball曲线的两种扩展，并分析了这两类曲线与Bézier曲线的关系。文献[4-5]提出了三次、四次Ball曲线的扩展，通过增加t的次数，得到的曲线具有Ball曲线类似的几何性质。文献[6-7]提出的四次、五次Wang-Ball曲线，包含了Wang-Ball与Said-Ball曲线之间的过渡曲线及Said-Ball与Bézier曲线之间的过渡曲线。

构造了带3个形状参数的五次Wang-Ball型曲线，曲线包含了五次Wang-Ball曲线到五次Said-Ball曲线及五次Bézier曲线的过渡曲线，具有Ball曲线类似的几何性质，并包含了文献[7]中的αB曲线。

1曲线的构造及性质

定义1对t∈[0,1]，1≤α≤3，α-2β-γ≥-2且α-β+γ≤1，称关于t的多项式

(1)

为带参数α,β,γ的五次Wang-Ball型基函数。

上述Wang-Ball基函数具有下列性质：

性质1非负性和规范性。对任意t∈[0,1]，1≤α≤3，α-2β-γ≥-2且α-β+γ≤1，wi5(t)≥0,i=0,1,2,3,4,5，且w05+w15+w25+w35+w45+w55=1。

性质2对称性。w05(t)=w55(1-t),w15(t)=w45(1-t),w25(t)=w35(1-t)。

性质3端点性质。

性质4单调性。当t∈[0,1]时，w05(t)、w55(t)关于α单调递减，w15(t)、w25(t)、w35(t)、w45(t)关于α单调递增；w05(t)、w55(t)关于β单调递增，w15(t)、w45(t)关于β单调递减；w05(t)、w55(t)关于γ单调递减，w15(t)、w45(t)关于γ单调递增。

性质5退化性。当α=3,β=3,γ=1时，五次Wang-Ball型基函数退化为五次Bernstein基函数；当α=1,β=0,γ=0时，五次Wang-Ball型基函数退化为五次Said-Ball基函数(图1)。

图1　五次Wang-Ball基函数图形(α=1,β=1,γ=1)Fig.1　Quintic Wang-Ball basis function graph (α=1,β=1,γ=1)

定义2给定6个控制顶点Pi∈Rd,d=2,3,i=0,1,2,3,4,5,1≤α≤3，α-2β-γ≥-2且α-β+γ≤1，对任意t∈[0,1]曲线

(2)

称式(2)为带形状参数的五次Wang-Ball型曲线。当α=3,β=3,γ=1时，曲线退化为五次Bézier曲线；当α=1,β=0,γ=0时，曲线退化为五次Said-Ball曲线；当β=γ=0时，退化为文献[7]定义的αB曲线。

图2给出了五次Wang-Ball曲线、五次Said-Ball曲线及五次Bézier曲线之间的过渡曲线。

图2　五次Wang-Ball、Said-Ball及Bézier曲线Fig.2　Quintic Wang-Ball、Said-Ball and Bézier curve

2形状参数的几何意义

(1) 当参数α、β固定，γ增大时曲线越来越靠近控制多边形。如图3(a)所示由内到外依次为α=3，β=1，γ=-3,-2.5,-2,-1.5,-1时的曲线。

(2) 当参数α、γ固定，β增大时曲线越来越扁平。如图3(b)所示由内到外依次为α=1，γ=1，β=2,1.75,1.5,1.25,1时的曲线。

(3) 当参数β、γ固定，α增大时曲线越来越靠近控制多边形。如图3(c)所示由内到外依次为β=1，γ=-1，α=1,1.5,2,2.5,3时的曲线。当固定其中一个参数，改变另外两个参数时，曲线的调整将更加的灵活，如图3(d)所示由内到外依次为β=-1，α=1,1.5,2,2.5,3，γ=-5,-4.5,-4,-3.5,-3。

图3　不同参数值的五次Wang-Ball型曲线Fig.3　Quintic Wang-Ball curves of different parameter values

3曲线拼接

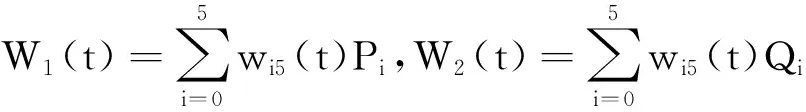
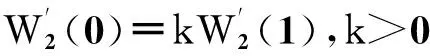
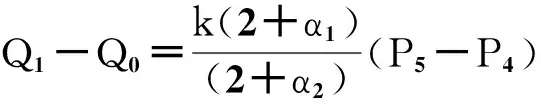
4应用实例

图4(a)由五次Wang-Ball曲线组成的开曲线

花瓣图形，曲线由内到外参数α=1,1.5,2,2.5,3，β=1，γ=-1。图4(b)由五次Wang-Ball曲线组成的闭曲线花瓣图形，曲线由内到外参数α=2，β=2,0,0，γ=1,-2,-1。

图4　花瓣图形Fig.4　Petal pattern

参考文献(References)：

[1] 施发中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2002,250-300

SHIFZ.ComputerAidedGeometricDesignandNon-UniformRationalB-spline[M].Beijing:HigherEducationPress,2002,250-300

[2] 邬弘毅.两类新的广义Ball曲线[J].应用数学学报,2000,23(2):196-205

WUHY.TwoNewTypesofGeneralizedBallCurves[J].JournalofAppliedmathematics,2000,23(2):196-205

[3] 严兰兰,梁炯丰,饶智勇.三次Ball曲线的两种新扩展[J].工程图学学报,2011,32(5):20-24

YANLL,LIANGJF,RAOZHY.TwoNewExtensionsofCubicBallCurve[J].JournalofEngineeringGraphics,2011,32(5):20-24

[4] 王成伟.三次Ball曲线的扩展[J].工程图学学报,2008,27(1):77-81

WANGCHW.ExtensionofCubicBallCurve[J].JournalofEngineeringGraphics,2008,27(1):77-81

[5] 王成伟.四次Wang-Ball曲线的扩展[J].工程图学学报,2009,30(1):80-84

WANGCHW.ExtensionofQuarticWang-BallCurve[J].JournalofEngineeringGraphics,2009,30(1):80-84

[6] 黄翠玲,黄有度.带双参数的四次Wang-Ball型曲线曲面[J].合肥工业大学学报,2012,35(10):1436-1440

HUANGCL,HUANGYD.QuarticWang-BallTypeCurvesandSurfaceswithTwoParameters[J].JournalofHefeiUniversityofTechnology,2012,35(10):1436-1440

[7] 严兰兰,张文,温荣生.两类形状可调五次广义Ball曲线 [J].工程图学学报,2011,32(6):16-20

YANLL,ZHANGW,WENRS.TwoClassesofQuinticGeneralizedBallCurveswithAdustableShape[J].JournalofEngineeringGraphics,2011,32(6):16-20

责任编辑：田静

doi:10.16055/j.issn.1672-058X.2016.0004.015

收稿日期：2015-02-02; 修回日期：2015-03-25.

*基金项目：安徽广播电视大学科研资金项目(QN15-01).

作者简介：张丹丹(1984-)，女，安徽安庆人，讲师，硕士研究生，从事计算机辅助几何设计研究.

中图分类号：TP391

文献标志码：A

文章编号：1672-058X(2016)04-0091-04

Extension of Quintic Wang-Ball Curve of with Parameters

ZHANGDan-dan,WUHuan-huan

(AnqingBranch,AnhuiRadioandTelevisionUniversity,AnhuiAnqing246001,China)

Abstract：A class of quintic Wang-Ball curve with three shape parameters α,β,γ is defined in this paper. This class of curve not only realizes the transition from quintic Wang-Ball curve to quintic Said-Ball curve and quintic Bézier curve, but also inherits the geometrical properties of quintic Ball curve. The geometrical meaning of shape parameters α,β,γ is analyzed and the shape of the curve can be adjusted flexibly. Some examples demonstrate the effectiveness of this method.

Key words：Wang-Ball curve; Said-Ball curve ；Bézier curve ；shape parameter; curve design