行星滚柱丝杠副螺纹牙均载设计方法研究

张文杰, 刘更, 佟瑞庭, 马尚君

(西北工业大学 陕西省机电传动与控制工程实验室, 陕西 西安　710072)



行星滚柱丝杠副螺纹牙均载设计方法研究

张文杰, 刘更, 佟瑞庭, 马尚君

(西北工业大学 陕西省机电传动与控制工程实验室, 陕西 西安710072)

摘要：为实现行星滚柱丝杠副(PRSM)的螺纹牙均载设计，使作用载荷尽可能在滚柱螺纹牙间均匀分布，从PRSM结构参数设计与螺纹精度设计2个层面展开研究。根据螺纹牙设计的弯曲与剪切强度条件与接触屈服条件，得到螺纹牙额定载荷与极限载荷计算方法以及PRSM参数设计准则。在参数设计层面，按照PRSM参数设计的一般流程，采用单因素方法研究了主要设计参数对载荷分布的影响规律，揭示了设计参数对载荷分布影响的基本规律，用于指导均载设计中参数优化。结果表明，各参数优化设计的关键是使丝杠、滚柱与螺母三者的轴段刚度有利于载荷均匀分布。在螺纹精度设计层面，研究了服从不同正态分布的随机螺距误差对载荷分布的影响，基于其影响规律，提出螺纹精度设计与公差带位置控制方法，实现PRSM螺纹牙均载设计。

关键词：行星滚柱丝杠副；载荷分布；均载设计；参数设计；精度设计；公差带

行星滚柱丝杠副(planetary roller screw mechanism,PRSM)作为一种滚动螺旋传动装置，以承载能力大的显著优势，兼之具有高精度及长寿命等优点，广泛应用于海事、石油、化工、冶金及机床等行业[1-3]。PRSM工作时主要依靠丝杠、滚柱与螺母之间螺纹牙的啮合进行运动与动力的传递，螺纹牙工作面承受交变载荷，螺纹牙参数设计对承载性能及寿命有重要影响。另外，承载后变形引起的螺距变化将导致载荷在螺纹牙间分布不均匀。PRSM螺纹牙载荷分布是其承载特性的重要体现，将直接影响其运转平稳性、承载能力及使用寿命。为了使载荷在螺纹牙间均匀分布，提高PRSM在上述传递动力场合的工作性能，需对其进行均载设计。对于螺旋传动装置，均载设计是指通过对产品受力状态的理论分析和实验研究，优化产品设计，把外加载荷较平均地分摊到每个受载滚动体及滚动体的每个螺纹牙，力争做到“无零载”、“无过载”的均衡动力传递[4]。

目前，国内外关于PRSM的理论研究已有较多成果。参数设计方面，靳谦忠等[5]基于对PRSM运动关系的分析，给出了基本设计参数的确定方法；Ma等[6]对PRSM设计参数进行了深入研究，总结出参数设计必须满足的8个条件；性能分析方面，目前的研究主要集中在运动学[7-8]、轴向刚度[9]、摩擦力矩[10]、动态性能[11]以及传动效率[7,10]等方面。

PRSM螺纹牙载荷分布研究已有一定基础：杨家军等[12]以Hertz弹性接触理论为基础，将滚柱作为整体，建立了刚度模型，得到了载荷分布曲线；Jan等[13]将滚动体等效成承受剪应力的矩形单元，建立了载荷分布计算模型，并与有限元解进行对比；Jones等[14]通过直接刚度法建立了PRSM轴向刚度的弹簧组模型，在此基础上得到了螺纹牙载荷分布，并分析了滚柱个数与滚柱螺纹牙个数对载荷分布的影响；马尚君等[15]基于滚柱的等效球假设，通过建立递推关系得到了PRSM载荷分布规律，并基于所建立的载荷分布模型进一步建立了PRSM摩擦热与效率模型；张文杰等[16]考虑多种变形与支撑方式等因素，基于变形协调关系与受力平衡关系建立矩阵方程，得到了PRSM滚柱螺纹牙在丝杠侧与螺母侧载荷分布规律，并分析了螺纹牙型参数对载荷分布的影响。上述研究都揭示了PRSM螺纹牙载荷分布不均现象并得到了其分布规律。然而，如何在设计过程中选取合适的参数，在满足螺纹牙强度条件的同时使所设计的PRSM具有较好的载荷分布特性，实现螺纹牙均载设计，未见相关研究。

PRSM螺纹牙均载设计包含2层含义。首先，在结构参数设计过程中，需尽可能选择使载荷分布较为均匀的参数；其次，在加工过程中可根据需要进一步对螺纹精度进行主动设计，通过控制螺纹牙初始接触状态，实现PRSM均载设计。

本文首先根据螺纹牙剪切与弯曲强度条件及螺纹牙接触屈服条件得到螺纹牙额定载荷与极限载荷计算方法，以此作为螺纹牙均载设计需满足的条件；其次，按照PRSM一般设计流程，分析主要设计参数对螺纹牙载荷分布的影响规律，并得到均载设计方法及参数设计准则；最后，分析了不同螺距精度下载荷分布波动情况，提出通过控制螺纹精度与公差带位置改善载荷分布不均现象。

1PRSM螺纹牙型设计准则

关于PRSM基本参数设计，文献[5-6]已有详细说明。然而，对于如螺距及滚柱螺纹牙个数等重要螺纹牙型参数的设计，目前并无相关方法与研究。螺纹牙型参数对PRSM载荷分布有很大的影响[16]，并且牙型参数需满足螺纹牙强度准则以防止螺纹牙根位置发生断裂；需满足螺纹牙接触屈服准则以保证螺纹牙的接触处于弹性阶段，不会发生不可恢复的塑性变形，以提高PRSM疲劳寿命。本文总结PRSM螺纹牙型设计需满足的2个准则，并得到螺纹牙额定载荷与极限载荷计算方法，用于指导均载设计中牙型参数的设计。

1.1螺纹牙强度准则

为建立PRSM螺纹牙强度准则，首先需分析丝杠、滚柱与螺母三者螺纹牙的啮合。如图1所示，点划线表示丝杠、滚柱与螺母的中径，实线分别表示其大径与小径。3个圆之间重叠的区域，即表示滚柱分别与丝杠和螺母可能的啮合区域。

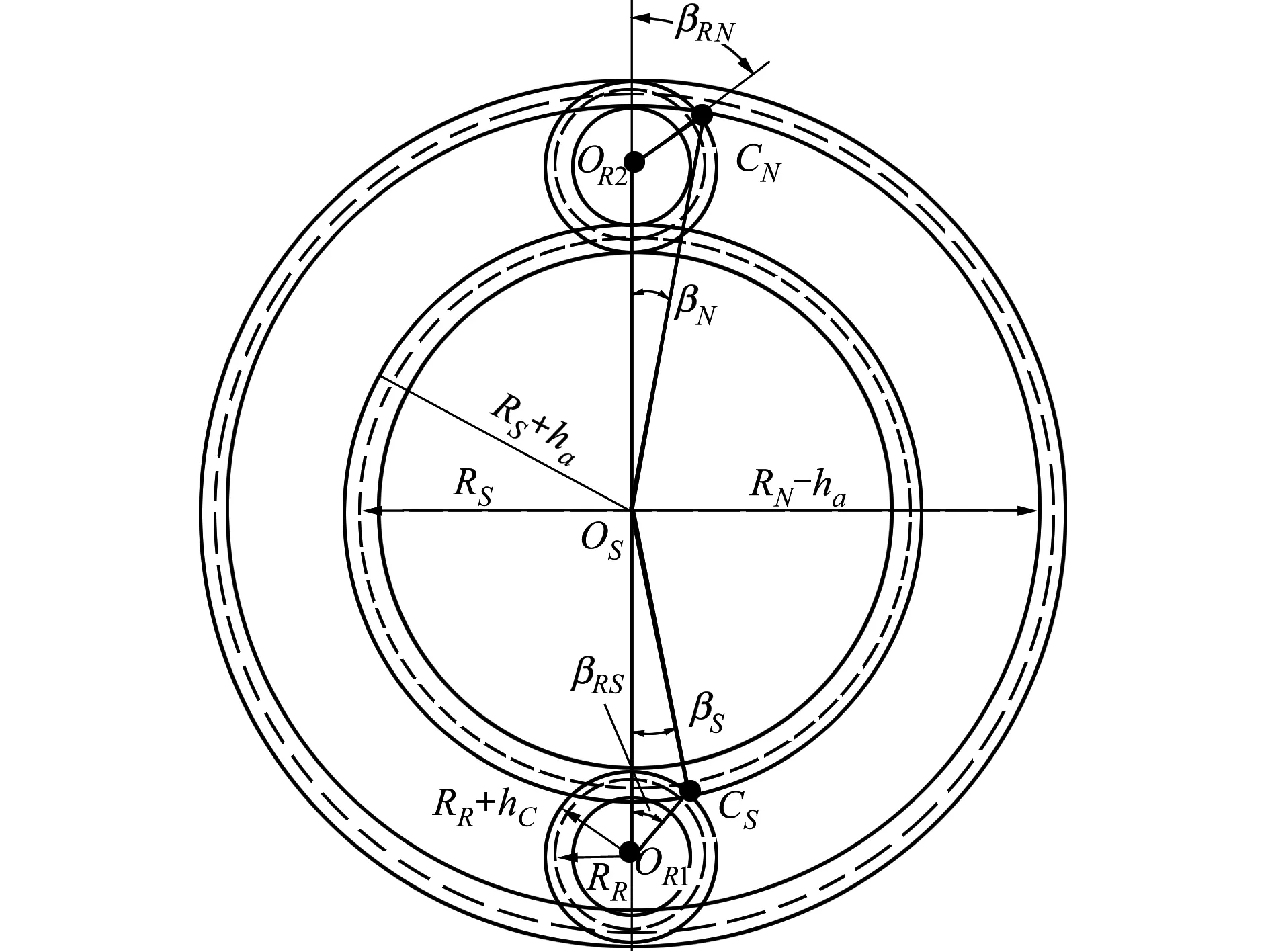
图1　PRSM螺纹啮合区域示意图

由图1中几何关系所示，在ΔOSOR1CS中,根据余弦定理得出

(1)

(2)

式中,βS为丝杠螺纹啮合半角、βRS为滚柱螺纹丝杠侧啮合半角。

在ΔOSOR2CN中,根据余弦定理得出

(3)

(4)

式中,βN为螺母螺纹啮合半角、βRN为滚柱螺纹螺母侧啮合半角。

图2　PRSM螺纹承载示意图

PRSM丝杠、滚柱与螺母间为点啮合,而啮合点附近区域的螺纹牙将因为承受载荷而发生弯曲与剪切变形。借鉴螺纹联接强度校核公式进行PRSM螺纹牙强度校核。将参与啮合的螺纹沿螺纹中径展开成如图2所示的悬臂梁形式[17],丝杠、滚柱或螺母螺纹牙承载部分的长度为

(5)

式中,βX为对应螺纹的啮合半角,RX为相应的螺纹名义半径。

螺纹牙危险截面m-m的剪切强度条件为

(6)

式中,τ为承载后螺纹牙底剪切应力,fa为螺纹牙承受的轴向载荷,c为螺纹牙根部厚度,l为螺纹牙承载部分长度,[τ]为材料的许用切应力。

螺纹牙危险截面m-m的弯曲强度条件为

(7)

式中,σ为承载后螺纹牙根弯曲应力,hf为螺纹牙底高,[σb]为材料的许用弯曲应力。

1.2螺纹牙接触屈服准则

由Hertz理论可知,两接触物体由于接触变形而产生的弹性变形量为[18]

(8)

公式(8)变形可得

(9)

两接触物体接触椭圆的长半轴与短半轴分别为

(10)

(11)

式中,a*与b*为与两接触体曲率函数相关的接触参数,可通过查表得到。

由公式(9)～(11)可得

(12)

对于接触椭圆区域,最大压应力在几何中心,其大小为

(13)

将(9)式、(12)式代入(13)式,并变形,得

(14)

由von Mises屈服准则[19]可知,其屈服极限为

(15)

式中,kst是与接触椭圆参数b/a有关的系数,取值介于0.30至0.33之间[20]。将(14)式、(15)式代入(9)式中得到螺纹牙不发生塑性变形的接触力

(16)

则PRSM螺纹牙不发生塑性变形的最大轴向力为

(17)

式中,αR为滚柱螺旋升角,θ为牙型角。

1.3螺纹牙额定载荷与极限载荷

定义PRSM螺纹牙额定载荷为某设计参数下螺纹牙不发生塑性接触变形以及破坏时可以承受的最大轴向载荷。定义螺纹牙极限载荷为螺纹牙不发生破坏时可以承受的最大轴向载荷。则由(6)式、(7)式及(17)式可得

(18)

(19)

式中,fc为螺纹牙额定载荷,fmax为螺纹牙极限载荷。

1.4PRSM参数设计准则

定义载荷分布不均系数为计算所得螺纹牙载荷与载荷均匀分布时螺纹牙载荷间的比值,即

(20)

式中,i为载荷分布不均系数,下标X可为S或N,分别表示丝杠侧和螺母侧,j表示螺纹牙序号,fave为螺纹牙平均载荷。

PRSM螺纹牙载荷分布规律是其设计参数的函数,max[iXj]为螺纹牙载荷分布不均系数最大值。显然,max[iXj]可以直观反映载荷分布不均匀的程度,其值越大,载荷分布越不均匀,并有

(21)

式中,等号右边括号内为PRSM全部设计参数,而列出的5个为影响最大的参数。在参数设计过程中,应使最大螺纹牙载荷小于螺纹牙极限载荷,即

(22)

式中,fmax为螺纹牙极限载荷。由于max[iXj]、fave、fmax三者都随着PRSM设计参数的变化而变化,因此,设计参数的确定需基于对传动性能、载荷分布等特性的综合考虑,再根据设计参数对载荷分布影响规律对各参数进行优化,直至螺纹牙载荷分布满足要求。

2PRSM均载设计方法之参数设计

本文采用一套承载能力为15 kN的PRSM,运用文献[16]建立的载荷分布分析模型,进行均载设计方法研究,基于各设计参数对螺纹牙载荷分布的影响规律,得到以均载为目标的各参数优化方向。PRSM结构参数如表1所示。在文中未做特别说明时,所有分析均以表1参数进行。PRSM中丝杠、滚柱与螺母材料均为GCr15，其弹性模量为212 GPa，泊松比为0.29。

表1　PRSM结构参数

2.1丝杠滚柱中径比k、滚柱个数z

PRSM丝杠中径与滚柱中径的比值k与丝杠螺纹头数的关系为[5]

(23)

式中,dS为丝杠中径,dR为滚柱中径,k为丝杠滚柱中径比,nS为丝杠螺纹头数。丝杠滚柱中径比k常见的取值及其与PRSM相关参数的关系如表2所示。其中,kSS/kSR为丝杠与滚柱轴段刚度比,其改变将会对PRSM螺纹牙载荷分布产生较大影响。

表2　丝杠滚柱中径比k与PRSM参数间的关系

选取k值分别为1、2、3,与之对应的滚柱个数为5、8、10,以及k值为4,与之对应的滚柱个数分别为9、12、15,进行载荷分布分析,结果如图3所示。

图3　不同k值下PRSM螺纹牙载荷分布

如图3a)与图3b)所示,丝杠侧载荷分布不均现象比螺母侧严重,随着k值的变大或滚柱个数的增多,丝杠侧与螺母侧载荷分布不均程度都将增加。另外,当选取较大k值时,滚柱与丝杠轴段刚度比较小,会使丝杠侧与螺母侧螺纹牙载荷间的相互影响作用变大。

由此可得,随着k值增大或滚柱个数z的增加,滚柱与丝杠的轴段刚度比将不利于载荷分布的均匀,但是随着可安装的滚柱个数逐渐增多,将降低单个滚柱、单个螺纹牙的载荷,有利于提高PRSM疲劳寿命。另外,丝杠、滚柱与螺母的螺纹头数、螺旋升角等参数会随着k值的变化而变化,将对PRSM啮合、传动效率及径向尺寸产生较大的影响。因此,设计时需综合考虑PRSM安装空间、传动特性及承载特性,选择合适的丝杠滚柱中径比k,待k值确定后通过进一步对其他参数的合理设计进行PRSM均载设计。

2.2螺距P

螺距是PRSM牙型参数中最重要的参数,将决定其它牙型参数。当丝杠中径与滚柱中径确定后,螺距的选择不仅对PRSM载荷分布有很大影响,也影响着螺纹零件加工成本的高低与精度控制的难易程度。选择不同螺距进行载荷分布分析,其结果如图4所示。

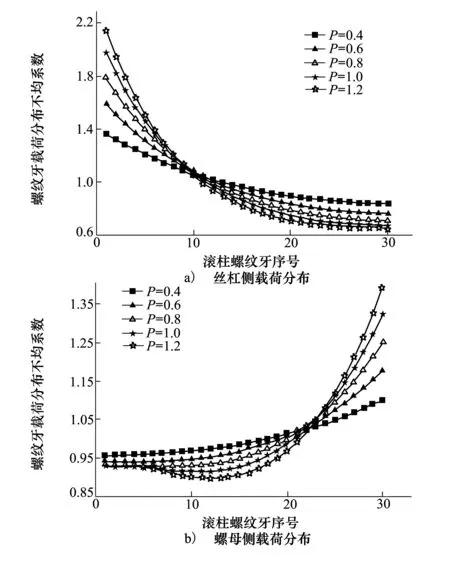
图4　不同螺距下PRSM螺纹牙载荷分布

如图4a)与图4b)所示,随着螺距的增大,丝杠侧与螺母侧的载荷分布不均程度都增加,丝杠侧从[0.83,1.36]变化为[0.64,2.13],螺母侧从[0.95,1.09]变化为[0.89,1.39]。另外,当螺距大于0.8以后,螺母侧载荷分布将出现明显的“两边大中间小”的现象。这是因为随着螺距的增大,丝杠与螺母轴段刚度变小,变形量增大,载荷分布不均匀程度增加,丝杠侧载荷与螺母侧载荷间的相互影响变大;同时丝杠、滚柱与螺母的轴段刚度变小,对丝杠侧与螺母侧载荷间的相互影响抵御能力降低。另外,由于一般情况下螺母的轴段刚度总是大于丝杠的轴段刚度,螺母侧对两侧载荷分布间的相互影响更加敏感,因此螺母侧载荷分布更容易出现“两边大中间小”的现象。

2.3滚柱螺纹牙个数n

螺距确定后,随之需要确定的参数就是滚柱螺纹牙个数。滚柱螺纹牙个数对PRSM载荷分布有着很大影响,已有研究表明,随着螺纹牙个数的增加,载荷分布不均匀程度增加。然而,过少的螺纹牙会使得螺纹牙平均载荷增大,使单个螺纹牙上接触应力太大,降低PRSM疲劳寿命。因此,需要通过研究给出螺纹牙个数设计的准则。给定螺纹牙个数分别为14、20、26、32、38,分析载荷分布,结果如图5所示。

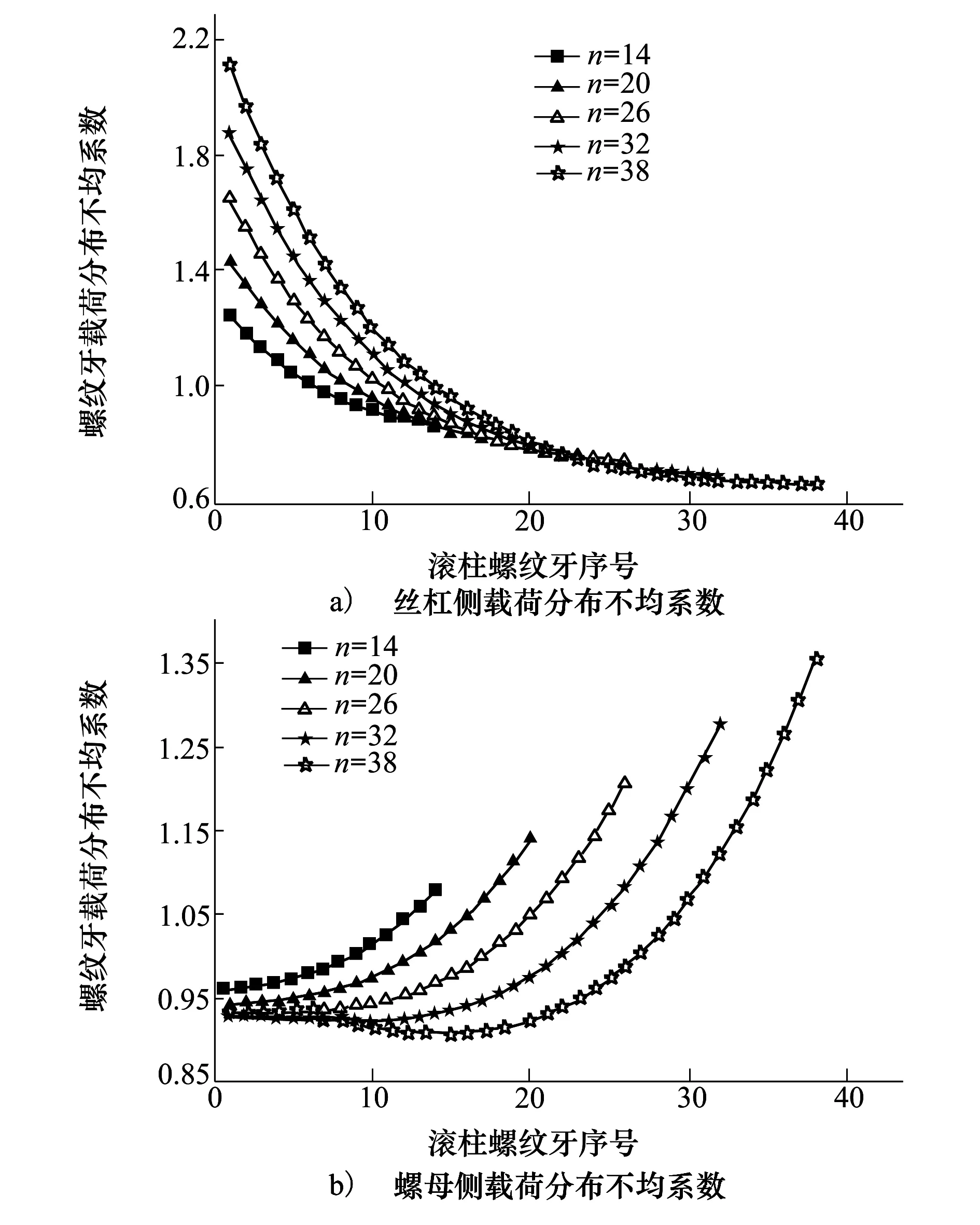
图5　不同螺纹牙个数下PRSM螺纹牙载荷分布

如图5所示,丝杠侧与螺母侧载荷分布不均匀程度都随螺纹牙个数的增加而增大,而丝杠侧载荷分布对螺纹牙个数的敏感性更大。另外当螺纹牙个数大于26以后,螺母侧载荷分布出现“两边大中间小”的现象。另外,滚柱螺纹牙个数也不能太少,使得单个螺纹牙承载太大。设计过程中需根据螺纹牙强度准则、接触屈服准则及PRSM参数设计准则判断螺距、螺纹牙个数等螺纹牙型参数是否合理。

2.4螺母外径Dout

螺母外径Dout决定PRSM径向尺寸的同时也影响载荷分布。为了在控制径向尺寸的同时得到较好的载荷分布,选择螺母外径Dout分别为26 mm、30 mm、35 mm、40 mm、45 mm,分析PRSM载荷分布,结果如图6所示。

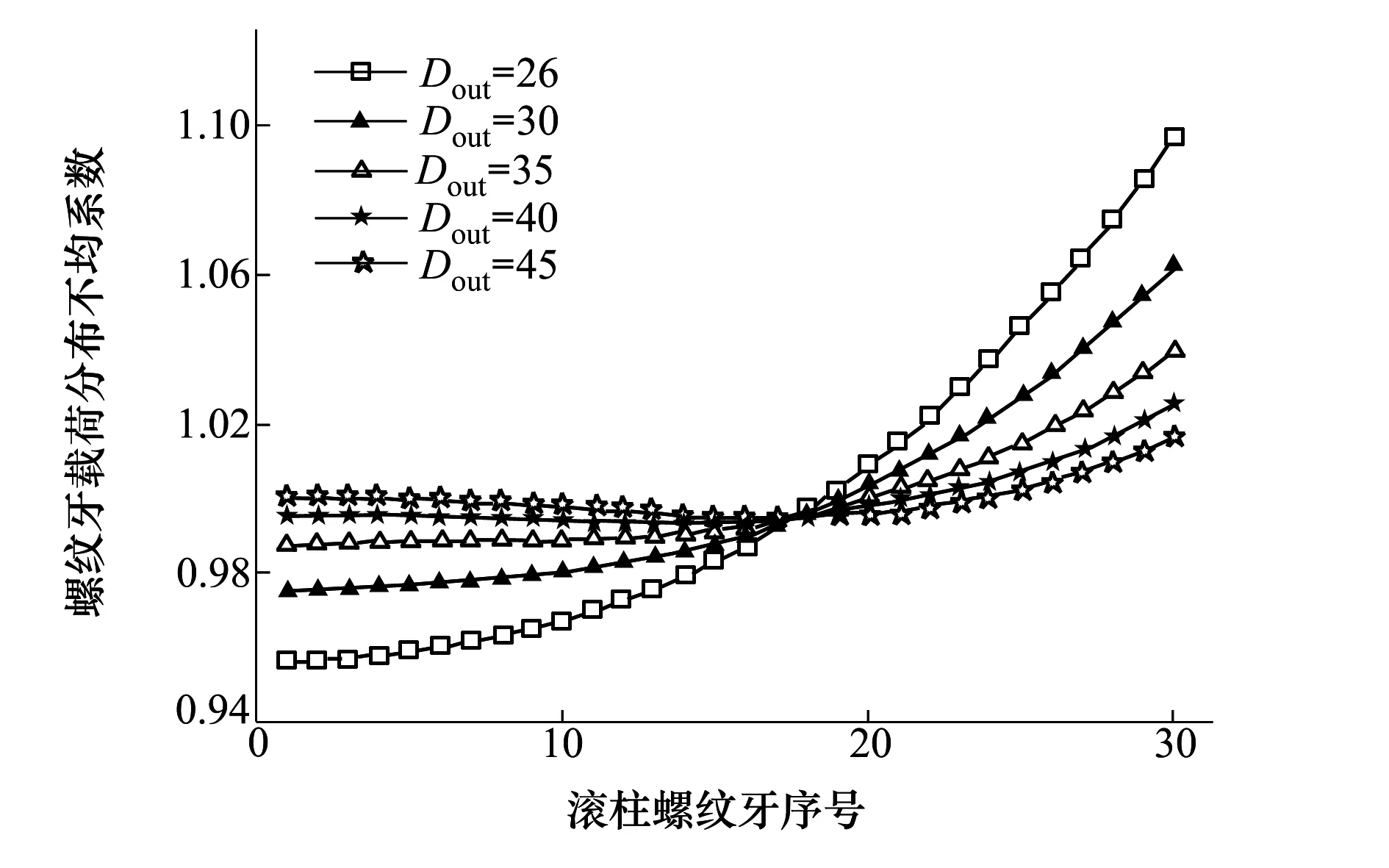
图6　螺母外径对螺母侧载荷分布影响

通过分析可知,螺母外径对于丝杠侧载荷分布影响很小,因此图6中仅给出螺母侧载荷分布的变化图。由图6可知,随着螺母外径的增大,螺母侧螺纹牙载荷分布趋于均匀;而当Dout大于40 mm以后,螺母侧载荷分布开始表现为“两边大中间小”。其原因是随着螺母外径的增大,螺母轴段刚度逐渐增大,载荷分布逐渐均匀;当螺母外径大于40 mm之后,螺母轴段刚度太大,变形困难,对于丝杠侧与螺母侧螺纹牙载荷间的影响更加敏感,导致出现“两边大中间小”的现象。

另外,尽管随着螺母轴段刚度的增大,螺母侧载荷分布区趋于均匀,但是螺母轴段刚度并非越大越好。否则,丝杠侧载荷分布不均,而螺母侧载荷分布均匀,后期通过加工精度与公差控制(3.2节),无法同时使两侧载荷趋于均匀。一般情况下,应使螺母外径保证螺母轴段刚度与丝杠轴段刚度在同一量级。

PRSM螺纹牙载荷分布不均现象是由于PRSM变形所产生的问题,由于轴段变形在轴向具有累积效果,而螺纹牙变形与接触变形发生在啮合点区域内,因此丝杠与螺母轴段变形对螺纹牙载荷分布起主导作用。要解决好载荷分布不均现象,即解决好轴段变形的问题,必须根据以上研究中各设计参数对PRSM螺纹牙载荷分布的影响规律,在设计过程对各参数进行优化与匹配设计。

3PRSM均载设计方法之精度设计

在理想设计条件下,丝杠侧与螺母侧螺纹牙在承受载荷后同时发生接触。然而,由于以螺距误差为主的螺纹误差的存在,滚柱与丝杠和螺母螺纹间的初始接触状态并不是理想的,即PRSM承载后,一部分螺纹先发生接触(承载),另一部分螺纹后发生接触(承载),甚至有的螺纹在满载情况下也不能接触,则发生所谓的“空载”。存在误差的情况下,丝杠、滚柱与螺母轴段刚度越大,螺纹间由误差引起的间隙越不容易被轴段变形补偿,则越容易出现过载与空载现象。因此,需根据PRSM丝杠、滚柱及螺母的轴段刚度对三者螺距误差进行控制,即进行精度设计。

3.1螺距精度控制

如图7所示,在随机给定的3组分别服从不同正态分布的螺距误差下,分析PRSM载荷分布,给出随机误差对于载荷分布的影响规律。

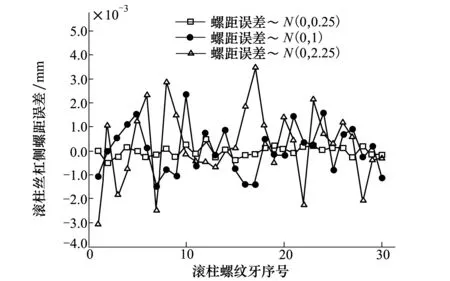
图7　滚柱螺距误差(丝杠侧)

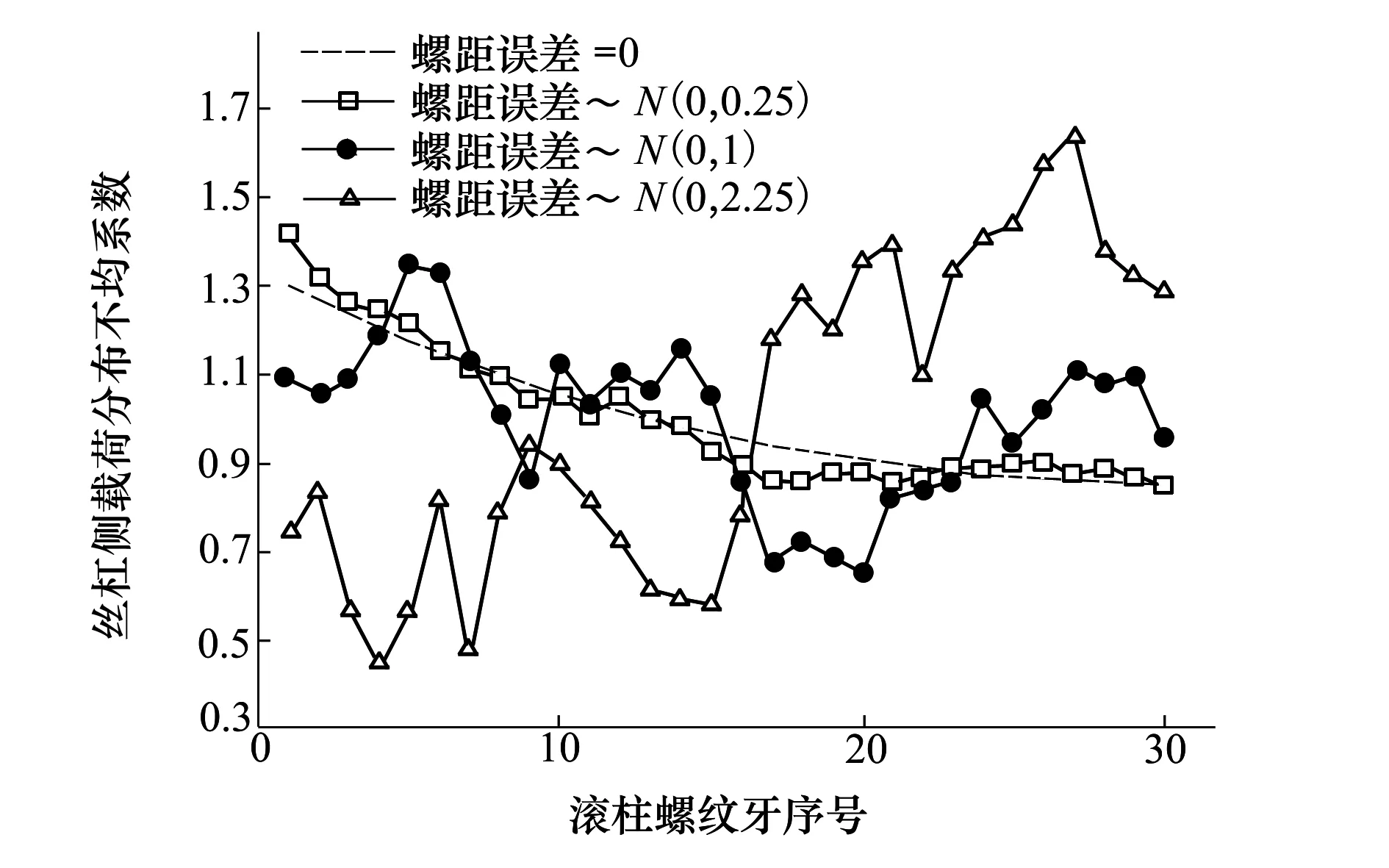
图8　不同螺距误差下丝杠侧载荷分布

图8所示为不同螺距误差下丝杠侧载荷分布,由图可知,当螺距误差服从不同正态分布时,丝杠侧载荷分布波动情况亦不相同。当螺距误差为正时,丝杠侧对应螺纹牙载荷上升;当螺距误差为负时,丝杠侧对应螺纹牙载荷下降。螺距误差的方差越大,载荷分布波动越大。当螺距误差服从N(0,0.25)时,载荷波动较小,其规律与未考虑误差时基本一致;当螺距误差服从N(0, 1)时,载荷波动较大,螺纹牙载荷分布不均现象加重;当螺距误差服从N(0, 2.25)时,载荷波动很大,第4、7个螺纹牙承载远小于平均载荷,而第26、27个螺纹牙载荷远大于平均载荷,出现“过载”,并且载荷分布变化趋势与未考虑误差时相反。另外,经过分析可知,由于在滚柱螺母侧,螺纹牙在与丝杠侧相反的牙侧接触,滚柱螺距误差对于螺母侧载荷分布的影响规律与丝杠侧相反。

本质上,螺距误差会对螺纹牙接触状态产生影响,进而影响载荷在螺纹牙间的分布,因此,PRSM螺纹零件需严格控制螺距误差。而载荷分布对于螺距误差的敏感性,会随着丝杠中径的增大或螺距的减小,即轴段刚度的增加而增加。因此,随着丝杠中径的增大,或随着螺距的减小,需提高螺纹加工精度,才能避免螺纹牙载荷出现太大波动。另外,螺距应该随着丝杠中径的增大而适当增大,以降低对丝杠螺距精度的控制要求。

3.2公差设计

显然,通过3.1节分析可知,螺距误差不仅会使螺纹牙载荷出现波动,也会使PRSM螺纹牙载荷分布基本规律发生根本改变。利用螺距误差对于螺纹牙载荷的影响规律,主动控制丝杠、滚柱与螺母的螺距精度及公差带位置,使得PRSM螺纹牙的初始接触状态有利于补偿丝杠与螺母轴段由于承载而产生的轴向变形,进而使载荷在PRSM螺纹牙间较均匀的分布,提高其使用寿命。公差的主动设计,与轴段刚度有直接关系,需根据PRSM额定载荷与承载后的轴段变形设计滚柱与螺母的精度等级与公差带位置。

如图9所示,根据分析给定丝杠侧与螺母侧螺距误差分别为服从N(0.15,0.25)和N(0.075,0.25)的随机误差,分析其载荷分布,结果如图10所示。由图10可知,在图9所示螺距精度设计下,PRSM螺纹牙载荷分布不均现象得到了较好的改善,丝杠侧与螺母侧载荷均呈现“两边大中间小”的分布规律,丝杠侧与螺母侧载荷分布不均系数区间分别为[0.96,1.08]与[0.98,1.02]。相比未进行精度设计时有很大改善。这是因为在图9所示的螺距误差下,丝杠、滚柱与螺母螺纹间的接触状态,可以较好的补偿丝杠与螺母由于承载而产生的轴段变形,使载荷分布变得均匀。

由此可见,为了使PRSM在丝杠侧与螺母侧的螺纹牙载荷趋于均匀,可以基于PRSM设计参数对丝杠,滚柱与螺母的螺距精度进行主动设计。由于丝杠的导程决定了PRSM系统导程,因此其螺距精度的控制应该最为严格,而滚柱与螺母的螺距公差带位置可以人为地进行调整,以期得到较好的载荷分布。

图9　丝杠侧与螺母侧螺距误差控制　　　　图10　公差主动控制下PRSM载荷分布

4结论

1) 本文基于PRSM牙型弯曲与剪切强度条件及接触屈服条件,得到螺纹牙额定载荷与极限载荷计算方法,基于此提出PRSM参数设计准则与螺纹精度控制方法,最终得到PRSM均载设计方法。PRSM设计时需综合考虑承载要求及传动要求等,基于均载设计方法进行参数设计、加工精度及公差带位置设计,使PRSM具有较好的载荷分布特性。

2) 研究得到PRSM丝杠滚柱中径比k值、滚柱个数z、螺距P、滚柱螺纹牙数n及螺母外径Dout对载荷分布的影响规律,并给出为保证载荷均匀分布的各参数的设计方法,其本质是通过参数设计,使丝杠、滚柱与螺母的轴段刚度匹配有利于载荷在螺纹牙间均匀分布。

3) PRSM螺纹零件需严格控制螺距误差,螺距精度越高,载荷分布波动越小,越不容易出现“过载”与“空载”的现象。载荷分布对螺距误差的敏感性随轴段刚度的增加而增加。因此,随着丝杠中径的增大,或随着螺距的减小,需提高螺纹加工精度,避免螺纹牙载荷出现太大波动。

4) 对螺纹牙螺距精度及公差带位置进行主动控制,使螺纹牙接触状态有利于补偿承载后丝杠与螺母的轴段变形,进而降低PRSM螺纹牙载荷波动并主动控制螺纹牙载荷分布规律,实现载荷分布的均化。精度要求及公差带位置需根据对PRSM承载后丝杠与螺母轴段累积变形量来确定。

参考文献：

[1]Brandenburg G, Brückl S, Dormann J, et al. Comparative Investigation of Rotary and Linear Motor Feed Drive Systems for High Precision Machine Tools[C]∥Proceedings of the Sixth International Workshop on Advanced Motion Control, Nagoya, Japan, 2000: 384-389

[2]Wang Hui, Tong Minhui, Zheng Pei. Research on Contact Strength between Roller Screw Pair on Hoisting Mechanism Applied in Deep Sea Crane[C]∥3rd International Conference on Applied Mechanics, Materials and Manufacturing, 2013: 2001-2005

[3]Boucher J Lutton. Roller Screws Crucial for Deep Sea Oil Rigs[J]. Ball Bearing Journal, 1985(12): 15-18

[4]黄祖尧. 绿色滚动功能部件在伺服进给系统中助推数控机床绿色制造[J]. 制造技术与机床,2013(3): 38-43

Huang Zuyao. Green Rolling Components in CNC Machine Tool Servo Feed System Boost Green Manufacturing[J]. Manufacturing Technology and Machine Tool, 2013(3): 38-43 (in Chinese)

[5]靳谦忠, 杨家军, 孙健利. 行星式滚柱丝杠副的运动特性及参数选择[J]. 制造技术与机床, 1998, (5): 13-16

Jin Qianzhong, Yang Jiajun, Sun Jianli. Motion Characteristics and Parameters Choosing of Planetary Roller Screw[J]. Manufacturing Technology and Machine Tool, 1998(5): 13-16 (in Chinese)

[6]Ma Shangjun, Liu Geng, Tong Ruiting, et al. A New Study on the Parameter Relationships of Planetary Roller Screws[J]. Mathematical Problem in Engineering, 2012(1): 1-29

[7]Velinsky S A, Chu B, Lasky T A. Kinematics and Efficiency Analysis of the Planetary Roller Screw Mechanism[J]. Mechanical Design, 2009, 131(1): 1-8

[8]Jones M H, Velinsky S A. Kinematics of Roller Migration in the Planetary Roller Screw Mechanism[J]. Mechanical Design, 2012, 134(1): 1-6

[9]马尚君, 刘更, 佟瑞庭, 等. 行星滚柱丝杠副轴向弹性变形的有限元分析[J]. 机械传动, 2012, 36(7): 78-81

Ma Shangjun, Liu Geng, Tong Ruiting, et al. Finite Element Analysis of Axila Elastic Deformation for Planetary Roller Screw[J]. Journal of Mechanical Transmission, 2012, 36(7): 78-81 (in Chinese)

[10] 马尚君,刘更,佟瑞庭. 行星滚柱丝杠副摩擦力矩及传动效率研究[J]. 哈尔滨工业大学学报, 2013, 45(11): 74-79

Ma Shangjun, Liu Geng, Tong Ruiting. The Frictional Moment and Transmission Efficiency of Planetary Roller Screw[J]. Journal of Harbin Institute of Technology, 2013, 45(11): 74-79 (in Chinese)

[11] 马尚君, 刘更, 周建星, 等. 行星滚柱丝杠副运转过程动态特性分析[J]. 振动与冲击, 2013, 32(3): 167-171

Ma Shangjun, Liu Geng, Zhou Jianxing, et al. Dynamic Characterisitic Analysis of Planetary Roller Screw in Operating Process[J]. Journal of Vibration and Shock, 2013, 32(3): 167-171 (in Chinese)

[12] 杨家军, 韦振兴, 朱继生, 等. 行星滚柱丝杠副载荷分布及刚度计算[J]. 华中科技大学学报, 2011, 39(4): 1-4

Yang Jiajun, Wei Zhenxing, Zhu Jisheng, et al. Calculation of Load Distribution of Planetary Roller Screws and Static Rigidity[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2011, 39(4): 1-4 (in Chinese)

[13] Jan Ryš, Lisowski F. The Computational Model of the Load Distribution Between Elements in Planetary Roller Screw[C]∥9th International Conference on Fracture & Strength of Solids, Jeju, Korea, 2013

[14] Jones M H, Velinsky S A. Stiffness of the Roller Screw Mechanism by the Direct Method[J]. Mechanics Based Design of Structures and Machines, 2014, 42: 17-34

[15] Ma Shangjun, Liu Geng, Tong Ruiting, et al, A Frictional Heat Model of Planetary Roller Screw Mechanism Considering Load Distribution[J]. Mechanics Based Design of Structures and Machines, 2015, (43): 164-182

[16] 张文杰, 刘更, 马尚君, 等. 不同安装方式下行星滚柱丝杠副载荷分布研究[J]. 西北工业大学学报,2015, 33(2): 229-236

Zhang Wenjie, Liu Geng, Ma Shangjun, et al. Load Distribution of Planetary Roller Screw Mechanism with Different Installations[J]. Journal of Northwestern Polytechanical University, 2015, 33(2): 229-236 (in Chinese)

[17] 濮良贵, 纪名刚. 机械设计[M]. 北京：高等教育出版社, 2006: 93-100

Pu Lianggui, Ji Minggang. Design of Machinery[M]. Beijing, China Higher Education Press, 2006: 93-100 (in Chinese)

[18] Johnson K. Contact Mechanics[M]. Cambridge University Press, 1985: 84-104

[19] 王仲仁, 苑世剑, 胡连喜, 等. 弹性与塑性力学基础[M]. 哈尔滨：哈尔滨工业大学出版社, 2007: 84-97

Wang Zhongren, Yuan Shijian, Hu Lianxi, et al. Fundamentals of Elasticity and Plasticity[M]. Harbin, Harbin Institute of Technology Press, 2007: 84-97 (in Chinese)

[20] Harris T A, Kotzalas M N. Rolling Bearing Analysis[M]. Fifth Edition. New York, Taylor & Francis Group, LLC, 2007: 104-120

收稿日期：2015-10-27基金项目：国家自然科学基金(51275423,51505381)、教育部高等学校博士学科点专项科研基金(20126102110019)、高等学校学科创新引智计划(B13044)与西北工业大学基础研究基金培育类项目资助。

作者简介：张文杰(1988—)，西北工业大学博士研究生，主要从事行星滚柱丝杠副设计、制造及其承载特性的研究。

中图分类号：TH132.1

文献标志码：A

文章编号:1000-2758(2016)03-0499-09

Thread Load Balance Design Method of Planetary Roller Screw Mechanism

Zhang Wenjie, Liu Geng, Tong Ruiting, Ma Shangjun

(Shaanxi Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi′an 710072)

Abstract:In order to achieve thread load balance design of planetary roller screw mechanism (PRSM), i.e. to make the applied load uniformly distributed among the threads of roller, two sections which include structural parameters design and thread tolerance design are studied in this paper. Firstly, two criteria are presented to guide the parameters design of thread form, which include intensity criterion and yield criterion of contact, and base on which, the rated load and limit load of thread and the criteria of parameter design are developed. Secondly, the effects of parameters of PRSM on load distribution are investigated by univariate analysis, and the nature of effect of parameters on load distribution are obtained. Results show that the nature of parameters optimal design is to search for a combination of shaft section stiffness of screw, roller and nut which can help to reach a uniform load distribution. Lastly, the effects of pitch deviations that obey normal distribution on load distribution are investigated, and approach of tolerance design are presented, which is identified to be effective to reach a uniform distribution of applied load among threads of roller.

Keywords:planetary roller screw mechanism; load distribution; load balance design; parameter design; precision design; tolerance zone