基于损伤力学模型的概率疲劳寿命预测方法

刘潇然, 孙秦

(西北工业大学 航空学院, 陕西 西安　710072)



基于损伤力学模型的概率疲劳寿命预测方法

刘潇然, 孙秦

(西北工业大学 航空学院, 陕西 西安710072)

摘要：基于金属结构危险点复杂应力状态下的疲劳损伤演化模型,利用材料的p-S～N曲线等对其部分损伤参数和材料参数进行概率化处理,提出了一种通过随机抽样计算危险点概率裂纹形成寿命的方法,讨论了损伤演化模型参数的基本概率特性以及相关性概念,采用拉丁超立方抽样方法实现了概率损伤参数的随机抽样,由此进行不同采样点的疲劳损伤累积,继而得到危险点的疲劳裂纹形成寿命。将损伤演化模型以UMAT子程序的形式嵌入ABAQUS软件系统中,给定结构模型及疲劳加载历程,即可用于复杂结构的疲劳寿命分析。结合铝合金2024-T3直耳片的疲劳试验,对其危险点的疲劳损伤及裂纹形成寿命概率分布进行了数值计算,初步表明了新算法模型的合理性。

关键词：损伤演化模型;概率裂纹形成寿命;拉丁超立方抽样;疲劳损伤累积

疲劳破坏是工程机械零构件失效的主要形式之一,现行的工程估算方法并不能深入探究其疲劳损伤的累积过程,因而预测精度偏低。现代损伤力学和有限元方法的结合可为复杂结构高应力危险点的疲劳损伤累积机理提供合理的数值计算方法,提高了疲劳寿命的预测精度。

连续损伤力学方法通过定义“损伤变量”来描述材料的疲劳行为,能够较好地反映“损伤使材料性能不断劣化”这一物理事实,在疲劳分析中得到了越来越多的应用[1-2]。损伤力学-有限元方法能够方便地实现材料内部损伤与其他状态变量(如应力、应变等)的关联,近年来在疲劳寿命的预测中得到了越来越多的应用,T.W.Kim等在J.L.Chaboche提出的损伤演化方程基础上进行了镍基合金的高温疲劳蠕变寿命预测[3];R.Desmorat等对准脆性材料的各向异性损伤模型和金属材料的高周疲劳双尺度损伤模型进行了研究,并给出了数值模拟方法[4];唐雪松等通过损伤力学-有限元方法对轴对称构件的疲劳寿命进行了预测[5];张淼等采用损伤力学方法预测了无扩口管路连接件的疲劳寿命[6]。

然而,上述研究大都属于确定性分析的范畴,对疲劳寿命的分散性考虑甚少,损伤演化方程参数仅通过中值S～N曲线拟合获取,并未考虑不同可靠度下的p-S～N曲线,获得的损伤演化方程中的参数是确定的值;另一方面,由于制造工艺等原因,相同材料的不同试件之间的某些力学参数也存在差异,如极限强度,上述研究并未考虑此对疲劳寿命的影响。确定性分析虽可以描述疲劳损伤失效的基本规律,但却不能体现疲劳寿命的概率特性,因此在疲劳寿命分析和计算中引入概率方法已成为必然[7-8]。

鉴于此,本文在修正的Lemaitre高周疲劳损伤演化方程的基础上,综合考虑以上因素对疲劳寿命分散性的影响,将损伤演化方程中的部分损伤参数及材料参数概率化,通过拟合p-S～N曲线获得损伤参数的概率特征,结合有限元软件建立了结构危险点高周疲劳寿命的概率计算模型。通过预估铝合金直耳片的寿命分布并与试验结果比较,说明了本方法的有效性。

1金属疲劳损伤的演化模型

近年来各国学者提出过很多不同的疲劳损伤演化模型,其中以法国学者Lemaitre于2005年提出的损伤演化方程应用最为广泛[9]。一个基于Lemaitre损伤演化方程的修正高周疲劳损伤演化方程如下所示[10]

(1)

式中,D为损伤变量,S为材料的损伤能量强度,s为描述损伤累积非线性的材料常数,E为弹性模量,σf为疲劳极限,细观三轴应力函数Rv为

(2)

式中,v为泊松比,σm为静水应力。

(1)式中,每个循环产生的累积等效塑性应变p为2(Δσ/E),PD为累积塑性应变门槛值,表示损伤并不是伴随着宏观塑性同时产生,而是当材料或者结构内部的能量累积到达临界值后才开始出现。

(3)

(4)

式中,R为应力比;c为与材料和构型有关的常数,铝合金光滑试样为1.60,铝合金缺口试样为1.40,结构钢光滑试样1.66,结构钢缺口试样2.16,钛合金光滑试样为1.66[11]。

此高周疲劳损伤演化方程可以很好地描述金属构件的疲劳损伤累积过程,本文将以此模型为基础针对疲劳寿命的概率计算方法展开研究。

2概率疲劳寿命的算法设计思想

(1)式以塑性应变损伤门槛值来判断损伤的产生,累积等效塑性应变p到达塑性应变损伤门槛值PD之前不产生疲劳损伤,之后损伤开始产生并不断累积,当损伤到达失效阈值Dc时材料发生破坏,失效判据如下所示

(5)

在材料力学性能试验时,相同条件下同类材料的不同试件得到的材料力学参数一般会有差异,但对于同一个试件应该只有一组确定的力学参数;材料损伤参数既然是材料力学性能劣化的一种表征,则应同其他材料力学参数一样具有上述性质。本文认为同类材料的损伤参数在不同试件之间的差异性才是疲劳寿命分散性产生的主要原因。

2.1材料损伤参数的概率化及获取方法

材料的部分损伤参数是服从一定概率分布的随机变量,称这些损伤参数为概率损伤参量。材料的弹性模量E和泊松比ν的分散性本身很小,在计算中做常数处理。因此本文将损伤演化方程中剩余的概率损伤参数分为以下3类:

1) 与损伤门槛值有关的:σu,m;

2) 与损伤演化有关的:σf,S,s;

3) 材料损伤失效阈值:Dc。

其中,σu和σf的概率特性可以通过材料的静力拉伸试验或者直接查相关手册获得,疲劳损伤失效阈值Dc可根据断裂应力σr与极限应力σu的值求出

(6)

可通过静强度断裂试验获得,对于金属材料Lemaitre建议取0.2～0.5[9]。

一般情况下高周疲劳损伤的非线性累积较弱,取s=1。对于剩余的2个参数m和S,当应力水平和其他参数确定时,由损伤演化模型可知材料疲劳寿命N是m和S的函数,即

(7)

另一方面,当应力水平确定时,疲劳寿命Nf又可以通过材料p-S～N曲线查到。m和S的取值应当使计算疲劳寿命N与实际疲劳寿命Nf尽可能的接近,据此可确定m和S的最优解应满足下式

(8)

在p-S～N曲线上取k个疲劳寿命Nf,采用SQP优化算法便可解得k组m和S的值,由于m和S之间可能并不独立,其相关性系数可通过对上述解得k组值进行相关性分析获得。该方法的前提是认为结构疲劳破坏寿命与其刚达到损伤阈值的寿命相同,忽略了裂纹扩展寿命,这在高周疲劳问题中是可以接受的。

最后,上述各概率损伤参数的分布特征均可通过概率分布假设检验获得。

2.2概率损伤参量的抽样技术

对于独立的概率损伤参量,选择合适的抽样方法即可进行抽样。本文采用的拉丁超立方抽样方法(LHS)能够避免一般蒙特卡罗方法大量重复的抽样工作,保证了样本采集的均匀性与唯一性,节省了抽样次数的同时也显著改善了数值模拟的精度,其过程如下[12-13]:

1) 对于任一随机变量X,首先确定对其抽样的次数n,然后将目标变量的概率分布函数分为n个互不重叠且概率相等的子区间,如图1所示。

图1　LHS抽样的子区间划分

2) 在每个区间内进行独立等概率抽样,且每个子区间内仅产生一个随机数,第j个区间内的随机数应满足下式

(9)

式中，u为[0,1]区间内均匀分布的随机数,Xj表示变量X的第j个子区间内的随机数。

3) 对随机数Xj进行累积分布函数反变换可得到变量X的随机样本。

由于参数S和m之间并不独立,因此需首先将其等效地转换成独立的正态分布之后才能进行抽样。目前常用的转换方法为Nataf转换[14],Nataf转换具有精度高和适用范围广的优点,其基本原理如下所示。

设有n维标准正态随机变量Y=(Y1,Y2,…,Yn)T,Y的相关系数矩阵为ρ0=(ρ0ij)n×n,相应的联合概率密度函数为

(10)

定义n维随机变量X=(X1,X2,…Xn)T,其相关系数矩阵为ρ=(ρij)n×n。根据等概率变换原则可得X和Y中的变量有如下函数关系

(11)

根据Nataf变换理论,利用隐函数求导法则可推导出变量X的联合概率密度函数为

(12)

根据相关系数定义及(11)式和(12)式可得变量X的相关系数与等效标准正态变量Y的相关系数有以下关系

(13)

当Xi和Xj的边缘分布函数及相关系数已知时,通过求解(13)式就可以确定等效相关系数。ρ0是一对称正定矩阵,对其进行Cholesky分解可得下三角矩阵Γ0,左乘Γ0的逆可将相关标准正态变量Y转化为独立标准正态变量U

(14)

至此,采用拉丁超立方抽样方法对独立标准正态变量U抽样,再对其进行上述变换的逆变换过程,即可得到对应的概率损伤参量的随机样本。

对各概率损伤参量按以上方法进行随机抽样,每组样本值即代表一个随机“试件”确定的损伤参数。

2.3疲劳损伤与有限元耦合算法

通过ABAQUS子程序UMAT将上节的损伤演化方程嵌入到有限元计算过程之中,通过考虑损伤值对材料弹塑性矩阵的影响,实现损伤与应力应变场的耦合,以反映材料损伤导致结构承载能力下降这一物理事实。

实现损伤与应力应变场耦合的具体方法如下:在一个循环结束后输出应力应变的同时利用损伤演化方程实时计算该次循环造成的损伤增量,之后更新损伤变量与寿命值,再将更新后的损伤值代入材料弹塑性矩阵Dep,这样在计算下次循环应力应变场时使用的是已经更新后的弹塑性矩阵Dep。当损伤累积到达失效阈值Dc后,通过将该单元材料属性中的弹性模量乘以一个趋零极小值来模拟该单元失效。考虑到疲劳循环次数一般比较大,如果每次循环后都计算一次损伤增量将耗费较长的计算时间,故在处理这一问题时作以下简化:在UMAT子程序内设一dN来表示计算中每个加载周期实际代表dN次循环(dN取值过小则需要较长的计算时间,过大又容易引入较大的计算误差,一般需依据预测寿命的量级来做调整,根据经验取材料疲劳寿命的1/20～1/50比较合适),任一单元到达损伤临界值时的加载周期数乘以dN就是该单元的计算疲劳寿命。

当结构和载荷条件一定时,计算每个随机“试件”的疲劳寿命便等同于独立完成一次数值疲劳试验,当“试件”数量足够大时统计多个“试件”的计算疲劳寿命便可获得其分布特征。

概率疲劳寿命算法的设计目标应使计算疲劳寿命的概率特征符合试验结果,算法的计算流程如下所示。

图2　概率疲劳寿命算法流程图

3试验验证

3.1试验件及试验结果

某直耳片试验件尺寸如图3所示。

图3　直耳片试件尺寸图

图中所标注尺寸单位为mm,耳片厚度为5.5mm,直耳片材料为铝合金2024-T3,弹性模量E取71 000Mpa,泊松比v取0.33。试验所加载荷谱如表1所示。

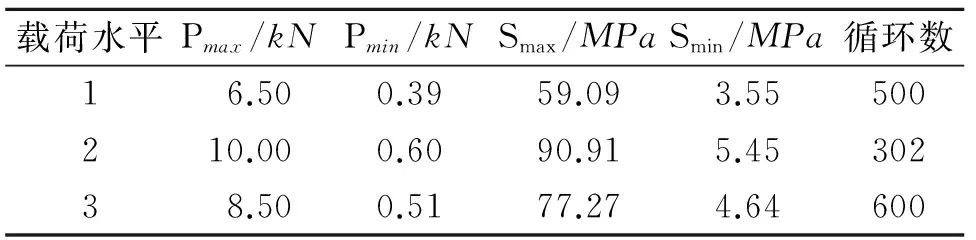
表1　直耳片疲劳载荷谱

试验机为MTS810.13±250kN电液伺服万能试验机,加载频率为20Hz,试验中耳片寿命为耳孔断裂时寿命。工程上一般认为疲劳寿命服从对数正态分布,试验结果及其对数均值和标准差如表2所示。

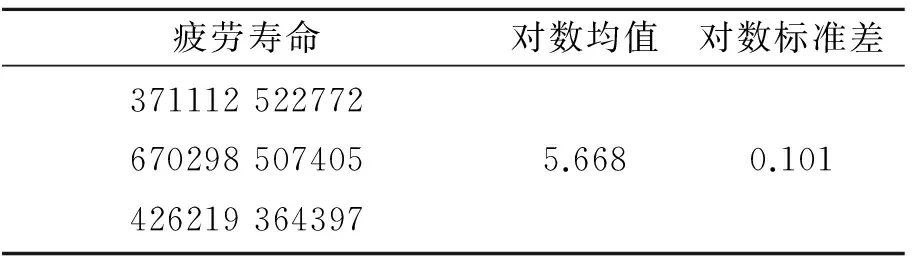
表2　直耳片疲劳试验结果

3.2建模及模型仿真

考虑耳片对称性沿长度方向选取一半建模如图4所示。模型左端面沿长度方向施加对称约束,其余2个方向位移约束,右端销钉上下表面施加切向载荷;销钉与孔内壁之间建立接触约束以保证应力能够通过接触面传递到耳片上的同时接触面之间又不发生穿透;网格划分采用8节点缩减积分体单元(C3D8R)。由于模型存在应力集中,故第一个达到损伤失效阈值的单元所加载循环数认为是构件危险点的裂纹形成寿命,这相当于将疲劳裂纹扩展一个单元长度时的寿命看成是结构危险点的裂纹形成寿命,疲劳裂纹剩余扩展寿命被忽略。如果单元过小,则忽略的扩展寿命越多,从而使得计算的寿命误差越大,单元过大,就会影响计算精度。一般情况下,裂纹扩展量达到0.5mm时,已经占据裂纹扩展寿命的大部分,而此时单元尺度的计算精度也较高,因此本文将孔边单元设定为0.5mm。

图4　直耳片有限元计算模型

对于铝合金2024-T3,损伤演化方程中概率损伤参量σu和σf的分布特征及其p-S～N曲线可通过现有资料[15]获得,S、m与损伤门槛值Dc的分布特征可通过(6)式和(8)式及分布假设检验获得,结果见表3,通过相关性分析得到S和m的相关性系数为0.348 4。

表3　铝合金2024-T3损伤参数分布特征

按照2.2节中的抽样技术,对上述概率损伤参量进行随机抽样,依次计算不同损伤参量样本组合对应的耳片危险点裂纹起始寿命,统计其分布特征,给出耳片计算裂纹起始寿命在不同置信度下的置信区间,并与试验数据进行对比以确定本文提出的概率疲劳寿命算法在工程应用中的可行性。表4分别给出了耳片计算疲劳寿命的对数均值和对数标准差。

表4　耳片计算疲劳寿命参数

由表2和表4可知,耳片计算疲劳寿命和试验疲劳寿命的对数均值误差为-0.26%,对数标准差误差为27.7%。两者的概率分布对比如图5所示。分别由计算值和试验值估计不同置信度下耳片疲劳寿命均值的置信区间临界值,计算结果见表5。

图5　计算疲劳寿命与试验疲劳寿命概率分布对比图

置信限阈值模型仿真试验90%上限734260683361下限27551831721295%上限805082734446下限25128129514899%上限967877848360下限209016255517

从表中结果可以看出,相同置信度下由模型计算得到的耳片疲劳寿命置信区间要比试验值的稍宽一些,这是因为计算疲劳寿命的对数标准差比试验值要大的缘故,说明此算法计算的疲劳寿命相对保守一些。除此之外,耳片的计算疲劳寿命与同等条件下的试验寿命相比,两者对数均值近似相等,而且试验疲劳寿命全部落在计算疲劳寿命的90%置信区间内,从统计学角度来讲精度已经很高,说明此方法可以较好地预测高周疲劳寿命的概率特性。

4结论

1) 在修正的高周疲劳损伤演化方程的基础上,将部分损伤参数及力学参数概率化,以铝合金2024-T3为例,通过拟合材料的p-S～N曲线得到损伤参数的概率分布特征。

2) 通过ABAQUS子程序UMAT将损伤演化方程嵌入到有限元计算过程之中,通过考虑损伤值对材料弹塑性矩阵的影响,实现损伤与应力应变场的耦合,以反映材料损伤导致结构承载能力下降这一物理事实,建立了疲劳寿命的概率计算方法。

3) 利用本文提出的数值方法对铝合金直耳片的疲劳寿命进行预估,数值计算结果与试验疲劳寿命的分布特征符合较好,表明该方法可以用于预测金属结构件的高周概率疲劳寿命。

参考文献：

[1]Van Do Vuong Nguyen, Lee Chinhyung, Chang Kyongho. High Cycle Fatigue Analysis in Presence of Residual Stresses by Using a Continuum Damage Mechanics Model[J]. International Journal of Fatigue, 2015, 70:51-62

[2]郭强, 郭杏林, 樊俊铃,等. 基于固有耗散的材料疲劳性能快速评估方法[J]. 力学学报, 2014, 46(6):931-939

Guo Qiang, Guo Xinglin, Fan Junling, et al. An Energy Approach to Rapidly Estimate Fatigue Behavior Based on Intrinsic Dissipation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 931-939 (in Chinese)

[3]Kim T W, Kang D H, Yeom J T, et al. Continuum Damage Mechanics Based Creep Fatigue Interacted Life Prediction of Nickel Based Superalloy at High Temperature[J]. Scripta Materialia, 2007, 57:1149-1152

[4]Desmorat R, Gatuingt F, Ragueneau F. Nonlocal Anisotropic Damage Model and Related Computational Aspects for Quasi-Brittle Materials[J]. Engineering Fracture Mechanics, 2007, 74(10):1539-1560

[5]唐雪松, 杨继运, 蒋持平,等. 轴对称构件疲劳寿命预测的损伤力学-附加载荷-有限元法[J]. 航空学报, 2002, 23(2):97-101

Tang Xuesong, Yang Jiyun, Jiang Chiping, et al. Damage Mechanics Additional Load Finite Element Method for Fatigue Life Prediction of Axisymmetrical Structural Members[J]. Acta Aeronoutica et Astronautica Sinica, 2002, 23(2): 97-101 (in Chinese)

[6]张淼, 孟庆春, 张行. 无扩口管路连接件疲劳寿命预估的损伤力学-有限元法[J]. 航空学报, 2009, 30(3):435-443

Zhang Miao, Meng Qingchun, Zhang Xing. Damage Mechanics Finite Element Method for Fatigue Life Prediction of Flare Free Pipeline Connection Assembles[J]. Acta Aeronoutica et Astronautica Sinica, 2009, 30(3): 435-443 (in Chinese)

[7]Xue Y. Modeling Fatigue Small Crack Growth with Confidence-A Multistage Approach[J]. International Journal of Fatigue, 2010, 32(7):1210-1219

[8]DuQuesnay D L, Underhill P R. Fatigue Life Scatter in 7xxx Series Aluminum Alloys[J]. International Journal of Fatigue, 2010, 32(2):398-402

[9]Lemaitre J, Desmorat R. Engineering Damage Mechanics[M]. Berlin, Springer, 2005:26-75

[10] 杨锋平, 孙秦, 罗金恒,等. 一个高周疲劳损伤演化修正模型[J]. 力学学报, 2012, 41(1):140-147

Yang Fengping, Sun Qin, Luo Jinheng, et al. A Corrected Damage Law for High Cycle Fatigue[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 41(1):140-147 (in Chinese)

[11] 刘建秀, 丁遂栋. 铝合金光试样非对称循环疲劳极限的估算[J]. 机械强度, 1999, 21(2):157-158

Liu Jianxiu, Ding Suidong. The Estimation of Nonsymmetry Cycle Fatigue Limits for Aluminum Alloy Smooth Specimens[J]. Journal of Mechanical Strength, 1999, 21(2):157-158 (in Chinese)

[12] 伍国军, 陈卫忠, 谭贤君,等. 基于拉丁超立方抽样的有限元可靠度程序开发及应用[J]. 岩土力学, 2015, 36(2):550-554

Wu Guojun, Chen Weizhong, Tan Xianjun et al. Program Development of Finite Element Reliability Method and Its Application Based on Latin Hypercube Sampling[J]. Rock and Soil Mechanics, 2015, 36(2):550-554 (in Chinese)

[13] 章晨璐, 赵晋泉, 罗卫华,等. 一种基于拉丁超立方采样的概率最优潮流算法[J]. 科学技术与工程, 2014, 14(14):49-53

Zhang Chenlu, Zhao Jinquan, Luo Weihua, et al. A Probabilistic Optimal Power Flow Calculation Method with Latin Hypercube Sampling[J]. Science Technology and Engineering, 2014, 14(14):49-53 (in Chinese)

[14] Der Kiureghian A, Liu P L. Structural Reliability under Incomplete Probability Information[J]. Journal of Engineering Mechanics, 1986, 112(1):85-104

[15] 中国航空材料手册编委会. 中国航空材料手册: 第3卷 铝合金、镁合金[M]. 北京: 中国标准出版社, 2002:297-308

Handbook of China Aeronautical Materials Editorial Committee. Handbook of China Aeronautical Materials: Vol. 3 Aluminum Alloy, Magnesium Alloy[M]. Beijing, Standards Press of China, 2002:297-308 (in Chinese)

收稿日期：2015-10-27

基金项目：国家自然科学基金(51375386)资助

作者简介：刘潇然(1990—)，西北工业大学博士研究生，主要从事飞行器结构疲劳行为研究。

中图分类号：V215.5+2

文献标志码：A

文章编号:1000-2758(2016)03-0424-07

The Prediction of Probability Fatigue Life Based on Damage Mechanics Model

Liu Xiaoran, Sun Qin

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:A method of predicting probabilistic crack propagation life through random sampling is proposed, which is based on fatigue damage evolution model under complex stress state for metal structures. Some damage parameters and material parameters are regarded as random variables through p-S～N curve. The probability properties of damage parameters are discussed. Latin hypercube sampling is used to generate random samples of these parameters. Fatigue damage accumulation process is simulated for different samples to get crack initiation life. When structure and load are determined, fatigue life for complex structure can be obtained by embedding damage evolution equation in ABAQUS. The probabilistic properties of fatigue life for aluminum alloys 2024-T3 straight lugs are obtained through this method which coincide well with fatigue test results, which shows the validity of the method.

Keywords:ABAQUS, aluminum alloys, crack propagation, damage evolution model, fatigue damage, fatigue damage accumulation, latin hypercube sampling, probability, probabilistic crack initiation life, random variables, sampling, stress