时滞依赖的中立型随机模糊系统的H∞控制问题

贾美多,苏亚坤,热贝嘉措

(1.锦州医科大学 公共基础学院，辽宁 锦州 121000； 2.渤海大学 数理学院，辽宁 锦州 121013)



时滞依赖的中立型随机模糊系统的H∞控制问题

贾美多1,苏亚坤*，2,热贝嘉措2

(1.锦州医科大学 公共基础学院，辽宁 锦州 121000； 2.渤海大学 数理学院，辽宁 锦州 121013)

摘要：研究了基于T-S模糊模型的中立型随机时滞系统的H∞控制问题.利用Lyapunov-Krasovskii泛函方法、Schur补引理和公式及并行分布补偿法(PDC),以线性矩阵不等式(LMI)形式给出了闭环系统H∞控制的新方法.最后，数值算例说明了该方法的有效性.

关键词：H∞控制；线性矩阵不等式(LMI)；中立型随机模糊系统；输入时滞

0引言

模糊系统和随机系统的控制问题被学者们广泛关注，过去的十多年中，关于这两个问题的结果已有很多文献报道.例如，随机系统控制理论与控制器设计得到了许多专家学者的关注〔1，2〕.文献〔3〕研究了时滞相关的随机系统的鲁棒镇定和H∞控制问题.状态时滞和滤波器设计问题已被文献〔4-5〕研究，文献〔6-9〕研究了常时滞和时变时滞的中立型随机系统的H∞控制问题.

1问题描述

考虑一类中立型T-S随机模糊时滞系统，定义模糊规则 如下：

IFθ1(t) is Ni1and … andθp(t) is Nip，THEN

d[x(t)-Dx(t-τ(t))]=[Ai(t)x(t)+Adi(t)x(t-τ(t))+B1i(t)u(t)+B1di(t)u(t-τ(t))

+Ev(t)]dt+[Hi(t)x(t)+Hdi(t)x(t-τ(t))+B2i(t)u(t)

+B2di(t)u(t-τ(t))]dω(t),

z(t)=Cix(t)+Cdix(t-τ(t))+B3iu(t)+B3diu(t-τ(t)),

x(t)=φ(t),∀t∈[-τ,0]

(1)

Ai(t)=Ai+ΔAi(t),Adi(t)=Adi+ΔAdi(t),B1i(t)=B1i+ΔB1i(t),B1di(t)=B1di+ΔB1di(t),

Hi(t)=Hi+ΔHi(t),Hdi(t)=Hdi+ΔHdi(t),B2i(t)=B2i+ΔB2i(t),B2di(t)=B2di+ΔB2di(t).

(2)

这里，i=1,2,…，N,M1,M2,N1i,N2i,N3i和N4i是适当维数的常矩阵；而F(·)：R→Rk×l是不确定矩阵满足FT(t)F(t)≤I.

最终中立型随机模糊系统可写为如下形式：

B1di(t)u(t-τ(t))+Ev(t)]dt+[Hi(t)x(t)+Hdi(t)x(t-τ(t))+

B2i(t)u(t)+B2di(t)u(t-τ(t))]dω(t)},

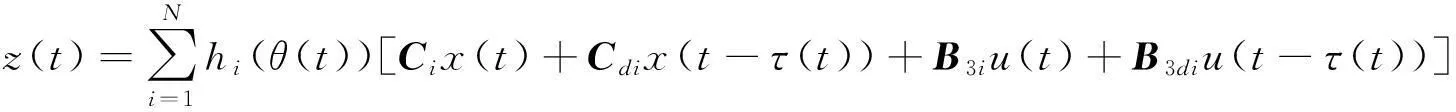
x(t)=φ(t),∀t∈[-τ,0]

(3)

引理〔10〕如果D和S是适当维数的实矩阵且W>0,对任意适当维数的矩阵x和y则有

2xTDSy≤xTDWDTx+yTSTW-1Sy

2主要结果

定理考虑中立型随机模糊时滞系统(3)，当v(t)≠0时，给定一个标量γ>0，如果存在矩阵Q>0,X>0,Yj和标量λ>0,使得下面线性矩阵不等式(LMI)成立，其中i,j=1,2,…，N，说明该系统在扰动衰减γ下是鲁棒随机稳定的.

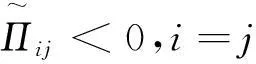
(4)

其中

随机模糊控制器设计为

(5)

证明构造如下形式的Lyapunov-Krasovskii泛函

(6)

B2i(t)u(t)+B2di(t)u(t-τ(t))]dω(t)}

(7)

B2di(t)u(t-τ(t))]TP[Hi(t)x(t)+Hdi(t)x(t-τ(t))+B2i(t)u(t)+B2di(t)u(t-τ(t))]}+

(8)

通过引理，得到

-2xT(t-τ(t))DTP[Ai(t)x(t)+Adi(t)x(t-τ(t))+B1i(t)u(t)+B1di(t)u(t-τ(t))+Ev(t)]

≤xT(t-τ(t))DTPDx(t-τ(t))+[Ai(t)x(t)+Adi(t)x(t-τ(t))+B1i(t)u(t)+

B1di(t)u(t-τ(t))+Ev(t)]TP[Ai(t)x(t)+Adi(t)x(t-τ(t))+B1i(t)u(t)+

B1di(t)u(t-τ(t))+Ev(t)]

(9)

通过(8-9)可以推断出

其中

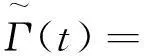
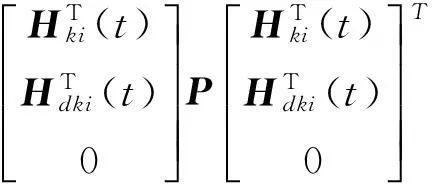
(10)

Aki(t)=Ai+B1iKj+ΔAki(t),Hki(t)=Hi+B2iKj+ΔHki(t),ΔAki(t)=ΔAi(t)+ΔB1i(t)Ki

ΔAki(t)=ΔAi(t)+ΔB1i(t)Kj，ΔHki(t)=ΔHi(t)+ΔB2i(t)Kj,Adki(t)=Adi+B1kiKj+ΔAdki(t),

Hdki(t)=Hdi+B2diKj+ΔHdki(t),ΔAdki(t)=ΔAdi(t)+ΔB1di(t)Kj,

ΔHdki(t)=ΔHdi(t)+ΔB2di(t)Kj

对(10)应用Schur补引理及引理得

(11)

Υ1=Ai+B1iKj,Υ2=Hi+B2iKj,Υ3=Adi+B1diKj,Υ4=Hdi+B2diKj

对式(11)前乘，后乘diag{P-1,P-1,I,I,I,I,I,I}

当t>0时定义

(12)

对(7)从0到t>0两边同时积分并取期望则有

(11)

把(13)代入(12)得

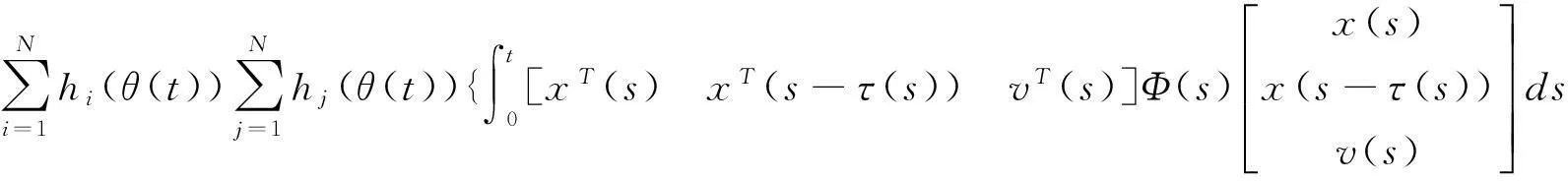
其中

很容易得到Φ(s)<0，所以J(t)<0，定理得证.

3数值算例

考虑中立型随机模糊系统(3)所给参数如下：

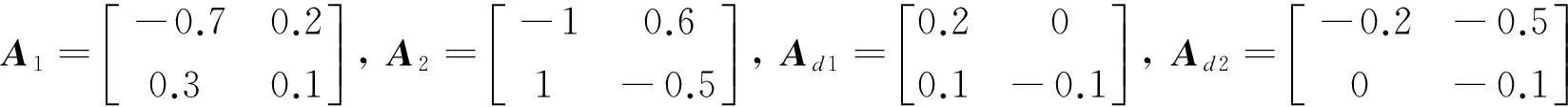
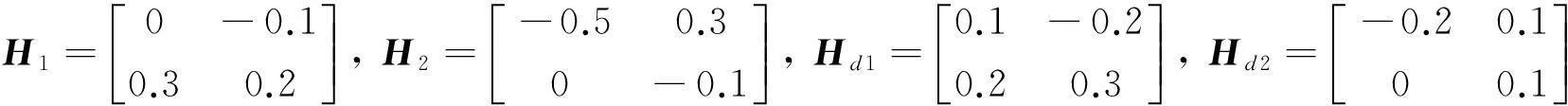
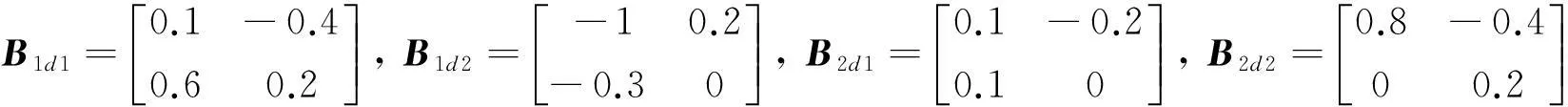
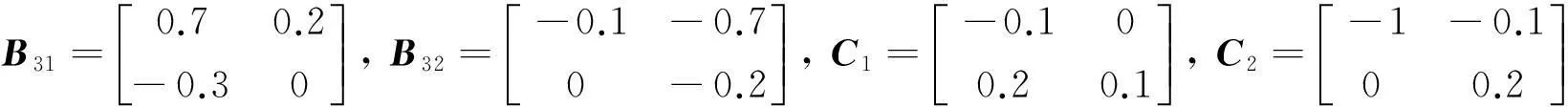
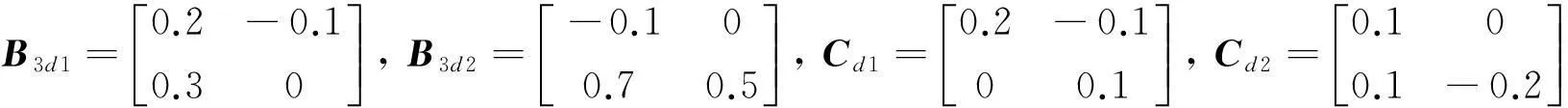
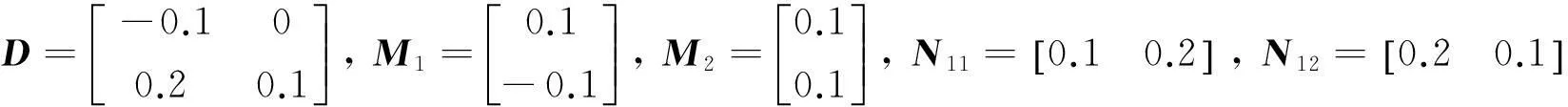
当γ=0.5时，运用LMI工具箱求解定理中的不等式，得到下面的解决方案

此时状态反馈控制器为

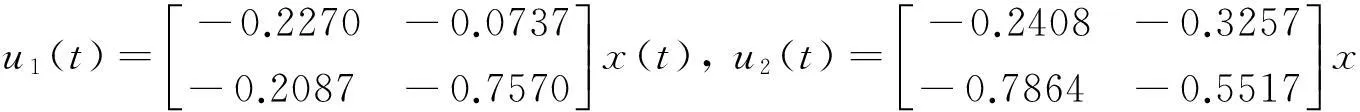
4结论

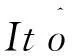
参考文献:

〔1〕蔡尚峰.随机控制理论〔M〕.上海: 上海交通大学出版社,1987.

〔2〕冯赞刚,郭治.随机控制〔M〕.北京: 国防工业出版社,1988.

〔3〕CHEN W H,GUAN Z H,LU X.Delay-dependent robust stabilization and H∞control of uncertain stochastic systems with time-varying delay〔J〕.IMA Journal Mathematical Control and Information,2004,21(3): 345-358.

〔4〕XU S,CHEN.T.Robust H∞control for uncertain stochastic systems with state delay〔J〕.IEEE Transactions on Automatic Control,2002,47(12): 2089-2094.

〔5〕CHEN B,CHEN W,WU H.Robust H2/H∞Global linearization filter design for nonlinear stochastic systems〔J〕,IEEE Transactions on Automatic Control,2009,56(7): 1441-1454．

〔6〕XU S Y,SHI P,CHU Y M.Robust stochastic stabilization and H∞control of uncertain neutral stochastic time-delay systems〔J〕.Journal of Mathematical of Analysis and Applications,2006,314(1): 1-16.

〔7〕CHEN G C,Wang X P.Robust H∞control for neutral stochastic uncertain systems with time-varying delay〔J〕.Journal of Systems Engineering and Electronics,2010,21(4): 658-665.

〔8〕XU S Y,Lam J,Yang C W.Robust H∞control for uncertain linear neutral delay systems〔J〕.Optimal Control Application Methods,2002,23(3): 113-123.

〔9〕苏亚坤，热贝嘉措.带有时变时滞的中立型随机系统的鲁棒镇定和H∞控制，渤海大学学报，2015,36(1): 24-31.

〔10〕WANG Y,XIE L,SOUZA C E D.Robust control of a class of uncertain nonlinear systems〔J〕.Systems and Control Letters,1992,19(2): 139-149.

Delay dependent H∞control for neutral stochastic fuzzy systems

JIA Mei-duo,SU Ya-kun,RE BEI Jia-cuo

(1.College Of Basic Science,Liaoning Medical University,Jinzhou 121000,China;2.School Of Mathematics And Physics,Bohai University,Jinzhou 121000,China)

Abstract：The problem of H∞control for neutral T-S stochastic fuzzy time-delay systems is discussed.By using the Lyapunov functional method,Schur complement lemma, formula and parallel distributed compensation(PDC),the closed loop system of H∞control is given by linear matrix inequality(LMI).Finally,numerical example shows that our method is efficient.

Key words：H∞control; Linear matrix inequality(LMI); neutral stochastic fuzzy systems with time-delay

收稿日期：2015-09-10.

基金项目：国家自然科学基金项目(No: 61403043).

作者简介：贾美多(1989-) ，女，助教，主要从事控制理论方面的研究.

通讯作者：jc335@qq.com.

中图分类号：TP13

文献标志码：A

文章编号：1673-0569(2016)02-0166-06