时变时滞的随机系统的L2-L∞滤波分析问题

王艳杰，闫玥岑，邓　雪，苏亚坤*，

(1.渤海大学 大学基础教研部，辽宁 锦州 121013； 2.渤海大学 数理学院，辽宁 锦州 121013；3.渤海大学 管理学院，辽宁 锦州 121013)



时变时滞的随机系统的L2-L∞滤波分析问题

王艳杰1，闫玥岑2，邓雪3，苏亚坤*，2

(1.渤海大学 大学基础教研部，辽宁 锦州 121013； 2.渤海大学 数理学院，辽宁 锦州 121013；3.渤海大学 管理学院，辽宁 锦州 121013)

摘要：研究了带有时变时滞的随机系统的L2-L∞滤波设计问题.选取适当的Lyapunov 泛函，引用自由权矩阵的方法，基于线性矩阵不等式的可解性提出了时滞相关的滤波器设计的充分条件.

关键词：L2-L∞滤波；线性矩阵不等式；随机系统；时滞

0引言

近年来，L2-L∞滤波受到了越来越多学者的关注，并且取得了丰硕的研究成果〔1-5〕,如在文献〔5〕中提到了通过建立适当的Lyapunov泛函,研究了带有常时滞的随机系统的L2-L∞滤波设计问题.

本文研究了带有时变时滞的随机系统的L2-L∞滤波设计问题.通过引用自由权矩阵，结合矩阵解耦及Schur补引理的方法，基于线性矩阵不等式的可解性提出了带有时变时滞的随机系统的L2-L∞滤波设计方法，使其应用更广泛.

1问题描述

考虑如下随机时滞系统：

(1)

其中x(t)∈Rn代表状态向量；v(t)∈Rp代表扰动输入且v(t)∈L2[0,∞)；y(t) ∈Rm是测量输出；z(t)∈Rq是可估信号；ω(t)是一维布朗运动，满足

ε{dω(t)}=0,ε{dω(t)2}=dt

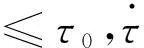
对(∑)系统，考虑下面的线性滤波器：

(2)

其中x(t)∈Rn是滤波状态，Af,Bf,Cf是需要设计的具有适当维数的滤波器矩阵.

令

综合(1-2)，可得如下滤波误差系统：

(3)

其中

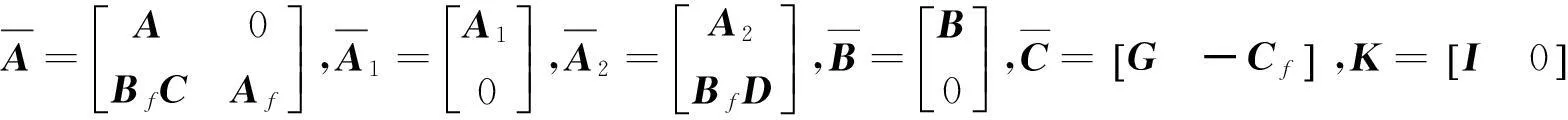
2主要结果

这部分将为随机时滞系统设计一个与时滞相关的L2-L∞滤波器，为此，首先提出了以下的结果：

定理1考虑随机时滞系统(∑).对于给定的标量γ>0，τ0>0，若存在矩阵P>0,Q>0,Z>0,M,H,使得下列线性矩阵不等式(4)成立，则称滤波误差系统(∑2)在任意的0≤τ(t)≤τ0下均方渐近稳定，并且满足L2-L∞滤波抑制条件：E{‖e‖∞}≤γ‖v‖2(γ>0,v∈L2〔0,∞)).

(4)

其中

(5)

证明在定理的条件下，首先证明误差系统的随机渐近稳定性，为此，我们考虑当v(t)=0时，

(6)

构造如下Lyapunov-Krasovskii泛函：

(7)

其中

(8)

通过伊藤微分公式，得

(9)

其中

(10)

记

ηT(t,α)=[ζT(t)ζT(t-τ(t))KTφT(α)KT]T

可以得到

其中

注意到

(11)

通过(9-11)可推出

通过(4)得到

通过Schur补引理给出

意味着

(12)

应用Schur补引理，得到

Ψ<0

(13)

下一步，考虑滤波误差系统L2-L∞性能指标，为此，在零初始条件下很容易看出

同样构造如(7)的Lyapunov-Krasovskii泛函并定义

其中t>0，可以得到

其中

φ(α)=Ax(α)+A1x(α-τ(t))+A2v(α)

对(4)应用Schur补引理，可以得到

J(t)<0

这意味着

通过Schur补引理，可以看出(5)满足

因此

由此说明不等式(5)成立，则滤波误差系统(∑2)满足L2-L∞性能指标.

现在，利用文献〔5〕类似的方法，给出L2-L∞滤波器时滞相关的充分条件.

定理2给定一个标量γ>0和随机时滞系统(∑).如果存在矩阵R>0,Q>0,Z>0,X>0.R1,R2,M,V,H满足以下线性矩阵不等式，则称L2-L∞滤波问题是可以解决的.

(14)

(15)

其中：

Δ1=RA+ATR+Q-M-MT

Δ2=RA+ATX+CTVT+R1+Q-M-MT

Δ3=XA+VC+ATX+CTVT+Q-M-MT

在此情况下，形如(2)的滤波器参数设计为

(16)

其中X1,Y1是任意的非奇异矩阵，满足

(17)

3结论

研究了带有时变时滞的L2-L∞滤波设计问题，通过构建适当的Lyapunov泛函，运用线性矩阵不等式，Schur引理，自由权矩阵以及矩阵解耦的方法，基于线性矩阵不等式得到了时滞相关的滤波器设计的充分条件.

参考文献：

〔1〕ZHANG B,LI Y.Exponential L2-L∞filtering for distributed delay systems with Markovian jumping parameters〔J〕.Signal Processing,2013,93(1): 206-216.

〔2〕KCHAOU,MOURAD,MANSOUR S,et al.Delay‐dependent stability and robust L2-L∞control for a class of fuzzy descriptor systems with time‐varying delay〔J〕.International Journal of Robust and Nonlinear Control，2013，23(3): 284-304.

〔3〕HUANG J,SHI Y,HUANG H,et al.L2-L∞filtering for multirate nonlinear sampled-data systems using TS fuzzy models〔J〕.Digital Signal Processing,2013,23(1): 418-426.

〔4〕CUI Y.L2-L∞Consensus control for high‐order multi‐agent systems with nonuniform time‐varying Delays〔J〕.Asian Journal of Control,2014,16(6): 1751-1759.

〔5〕XIA J,XU S,SONG B.Delay-dependent L2-L∞filter design for stochastic time-delay systems〔J〕.Systems & Control Letters,2007,56(9): 579-587.

L2-L∞filter design for stochastic system with time-varying delay

WANG Yan-jie1,YAN Yue-cen2,DENG Xue3,SU Ya-kun2

(1.Department of basic teaching,Bohai University,Jinzhou 121013,China;2.College of Mathematics and Physics,Bohai University,Jinzhou 121013,China;3.School of Management ,Bohai University,Jinzhou 121013,China;)

Abstract：The problem of L2-L∞filter design for stochastic system with time-varying delay is discussed in this paper.By adopting a suitable Lyapunov functional and introducing free-weighting matrix,a sufficient condition of delay-dependent L2-L∞filter design was given by linear matrix inequality(LMI).

Key words：L2-L∞filter； linear matrix inequality(LMI)； stochastic system; delay

收稿日期：2015-01-18.

基金项目：教育部人文社会科学规划基金项目(No:12YJA630023).

作者简介：王艳杰(1979-)，女，讲师，主要从事最优化理论及算法方面的研究.

通讯作者：380594753@qq.com.

中图分类号：TP13

文献标志码：A

文章编号：1673-0569(2016)02-0160-06