综合c-K条件岭估计及其优良性

王志福，刘佳瑞

(渤海大学 数理学院，辽宁 锦州 121013)



综合c-K条件岭估计及其优良性

王志福*，刘佳瑞

(渤海大学 数理学院，辽宁 锦州 121013)

摘要：对齐次等式约束的线性回归模型回归系数提出一个新的有偏估计-综合c-K条件岭估计.研究综合c-K条件岭估计的性质，并证明存在一定条件，使其在均方误差意义下优于约束最小二乘估计、条件岭估计、广义条件岭估计以及综合c-K条件岭估计.

关键词：综合c-K条件岭估计；线性回归模型；约束最小二乘估计；均方误差

0引言

下面为带有齐次线性等式约束的线性回归模型

(1)

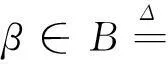
因为当设计矩阵X存在复共线性时，RLSE的均方误差会变得很大，性质很不理想.为改进RLSE，降低其均方误差，许多学者相继提出多种带齐次等式约束的有偏估计，并都得以证明这些估计是可容许估计且在均方误差意义下改进了RLSE〔2-5〕.宋永霞对无约束的线性回归模型

Y=Xβ+e,E(e)=0,Cov(e)=σ2In

(2)

1综合c-K条件岭估计定义及性质

定义1齐次等式约束线性回归模型回归系数的综合c-K条件岭估计为

HS-1,S=X′X.

引理1〔7〕在模型(1)下，W=W′,WSW=WSW′=W,其中

W=S-1-S-1H′(HS-1H′)-1HS-1

引理2〔7〕在模型(1)下，W为半正定矩阵，且W的秩为p-q.

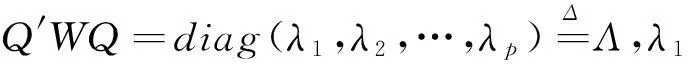
引理4〔9〕在模型(1)下，令α=Q′β=(α1，α2，…，αp)，则αp-q+1=αp-q+2=…=αp=0.

证明由于W为对称矩阵，且F(K)=diag(f1(k1),f2(k2),…fp(kp))为对称矩阵，故(QF(K)Q′W+cI)-1为对称矩阵，且(QF(K)Q′W+cI)-1W=W(QF(K)Q′W+cI)-1，则有

Q′W(QF(K)Q′W+cI)-1X′Y=Q′WQQ′(QF(K)Q′W+cI)-1X′Y=

ΛQ′(QF(K)Q′W+cI)-1X′Y

由Λ的定义可知性质4成立.

引入模型(1)的典则形式

(3)

其中Z=XQ，α=Q′β，L=HQ，从而Z′Z=Q′X′XQ=Q′SQ.故α的约束最小二乘估计(RLSE)为

Q′[S-1-S-1H′(HS-1H′)-1HS-1]-1QZ′Y=Q′WQZ′Y=ΛZ′Y

σ2(QF(K)Q′W+cI)-1[(QF(K)ΛQ′+cI)W(QF(K)ΛQ′W+cI)-W](QF(K)Q′W+cI)-1=σ2(QF(K)Q′W+cI)-1[(QF(K)ΛQ′)W(QF(K)ΛQ′)+2cWQF(K)ΛQ′+(c2-1)W]×(QF(K)Q′W+cI)-1

因为Q是正交矩阵，W≥0且fi(ki)≥0，则

(QF(K)ΛQ′)W(QF(K)ΛQ′)+2cWQF(K)ΛQ′+(c2-1)W≥0

2综合c-K条件岭估计的优良性

σ2tr(F(K)Λ+cI)-1Λ(F(K)Λ+cI)-1+‖[(F(K)Λ+cI)-1-I]α‖2=

根据以上证明，可以得出以下推论.

参考文献：

〔1〕王桂松.线性统计模型的理论及其应用〔M〕.合肥: 安徽教育出版社,1987.

〔2〕王志福,潘旭,金殊,等.假设检验原理及其应用〔J〕.渤海大学学报(自然科学版),2013,34(2): 101-105.

〔3〕栗丽,赵伟.王志福.在解决多重共线性问题上岭回归法比LS法的优越性〔J〕.渤海大学学报(自然科学版),2006,27(2): 124-126.

〔4〕林路.回归系数的综合岭估计〔J〕.数理统计与应用概率,1996,11(3)：179-184.

〔5〕王志福,范云.线性回归模型系数Stein估计的改进研究〔J〕.渤海大学学报(自然科学版),2009,30(3)：226-229.

〔6〕宋永霞.线性模型回归系数的一种有偏估计-综合c-K岭估计〔D〕.济南:山东大学，2014.

〔7〕史建红.约束线性回归模型回归系数的条件岭型估计〔J〕.山西师范大学学报(自然科学版),2001,15(4)：10-16.

〔8〕农丽秀,彭展声.约束线性回归模型回归系数的广义条件岭估计〔J〕.湘南学院学报(自然科学版),2008,29(5)：28-30.

〔9〕农丽秀.齐次等式约束线性回归模型回归系数的综合条件岭估计〔J〕.湖南师范大学(自然科学学报)，2012,35(2)：7-13.

The integrated c-K conditional ridge estimation and superiority

WANG Zhi-fu，LIU Jia-rui

(College of Mathematics and Physics，Bohai University，Jinzhou 121013，China)

Abstract：A new biased estimation of regression coefficient in a regression model with homogeneous equality constraints,the integrated c-K conditional ridge estimation,is proposed.The properties of the Integrated c-K conditional ridge estimation are studied,and under some conditions,it is proved that it′s better than the constrained least square estimation,the conditional ridge estimation,the generalized conditional ridge estimation and the integrated c-K conditional ridge estimation in the sense of the mean square error.

Key words：integrated c-K conditional ridge estimation; regression model; restricted least squares estimation; mean squares error

收稿日期：2015-08-10.

基金项目：国家自然科学基金项目(No:11671070).

作者简介：王志福(1960-),男,教授,主要从事应用概率与统计方面的研究.

通讯作者：liujiarui_169@163.com.

中图分类号：O212.2

文献标志码：A

文章编号：1673-0569(2016)02-0097-04