基于马尔柯夫模型的高校师资结构预测

高　路

(渤海大学 教改与教学质量评估中心，辽宁 锦州 121013)



基于马尔柯夫模型的高校师资结构预测

高路

(渤海大学 教改与教学质量评估中心，辽宁 锦州 121013)

摘要：教师是高校的主体，良好师资队伍结构是高校可持续发展的基础和前提.为了促进高校师资结构的合理配置,以马尔柯夫模型原理为基础，研究了预测过程并详细说明各步的计算方法；对某高校未来5年的师资结果进行预测和分析.结果表明，该预测模型可以有效地提高预测精度，由于系统各种状态的相互转移概率经常发生变化，该方法更适用于短期预测.

关键词：马尔柯夫模型；高校；师资结构；预测

0引言

马尔柯夫预测模型(Markov Forecasting Model)是根据俄国数学家马尔柯夫(A.A.Markov)的随机过程理论提出的一种市场预测方法.应用马尔柯夫链理论，根据研究对象的目前状态预测未来某个时刻或某个时期变动情况，是一种时间序列分析法.马尔柯夫模型作为一种预测技术已广泛应用于多个领域，包括音字转换、信息安全、词性自动标注和人力资源管理等〔1，2〕.

高校教师是国家的宝贵财富，是高等教育目标的实施者，高校教师水平决定着高校的教学与科研水平〔3〕.师资结构是影响高校教师队伍建设与发展的重要因素，合理的师资队伍结构对培养高质量人才具有重要作用.进入新世纪，国家高度重视高校师资队伍建设，建立了合理的职称评定制度和公平的绩效考核机制.很多高校也制定了科学的师资规划方案，积极探索改变师资结构的有效途径.目前高校的师资结构主要是由助教、讲师、副教授和教授构成.根据未来的教学和科研情况，对师资结构进行预测，解决高校教师培养的长远规划和实施问题.由于马尔柯夫链和马尔柯夫模型具有良好的数学基础作为支撑，所以它成为目前国内预测领域研究的热点问题.

本文基于马尔柯夫模型展开研究，进一步融合回归预测和最大期望算法(EMA，Expectation Maximization Algorithm)等优良算法，为高校师资结构预测提供一种新的解决思路.将预测结果作为高校教师引进和职称评定政策制定的依据，对促进高校师资结构的合理配置、提高教学科研水平等方面具有重要意义.

1马尔柯夫模型原理

状态是指客观事物可能出现或存在的状况，状态转移是指客观事物由一种状态到另一种状态的变化.对于一个系统，在由一种状态随机地转移至另一种状态的过程中，存在着转移概率，这种转移概率可以由前一种状态推算出来，而与该系统的原始状态和此次转移以前有限次数的转移无关，系统的这种状态转移称为马尔可夫过程(Markov Process)，是一类随机过程.

当状态和时间都处于离散状态时，这类特殊的马尔可夫过程也称为马尔柯夫链(Markov Chains).马尔可夫链是具有马尔可夫性质的随机变量的一个数列，通常用来建模排队理论和统计学中的建模，表达了两个随机变量之间的条件分布，不需要进行随机变量相关性分析〔4〕.由一种特定状态变化到另一种特定状态，就是过程实现了转移.最简单的情况只是两种状态之间转移，如图1所示.“状态1”保持“状态1”的概率为P11，“状态1”转移到“状态2”的概率为P12，“状态2”保持“状态2”的概率为P22，“状态2”转移到“状态1”的概率为P21.

马尔可夫链(Markov Chain)是具有马尔柯夫性质的随机变量序列.在当前状态已知的条件下，将来的状态可能与过去所处的状态A有关，也可能无关.若随机过程{x(t),t=0,1,2,…}的条件概率满足：

P{x(s)=j|x(t)=i,A}=P{x(s)=j|x(t)=i}

(1)

对于任何s>t及i=E,j=E成立，即与过去状态A无关，则称随机过程为马尔柯夫链.上述的这种特性称为无后效性.在较长时间下，该过程趋于稳定状态，与初始状态无关，称为稳定性.

如果系统的状态共有n种，系统由状态i一次转移到状态j的概率为pij，则系统一次转移概率的全体构成状态转移概率矩阵(State Transition Probability Matrix)，简称为概率矩阵，记为P，表示如下〔5〕：

(2)

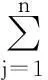
概率向量具有以下特点〔6-8〕：

(1)两个概率矩阵的乘积也是概率矩阵.

(2)概率矩阵的n次幂也是概率矩阵.

(3)当任一非零向量u=(u1,u2,…，un)左乘一方阵A后，结果仍为u.

(4)正规的马尔柯夫链是指经过若干次转移达到稳定状态后再转移时结果不会发生变化.这种稳定状态可以用行向量u表示：

u=(u1,u2,…,un),∑ui=1

(3)

行向量u也称为固定概率向量.

马尔可夫模型就在预测领域的应用就是通过对转移概率的研究确定变化趋势以预测未来.

2马尔柯夫模型预测过程

马尔柯夫模型预测过程共分为5步，如图2所示.

对图2各步描述如下〔9-11〕：

(1)构建状态空间.变量所有可能取值的集合称为“状态空间”.马尔柯夫链是具有马尔可夫性质的随机变量的一个状态序列,E1,E2,E3…，Ei的值是在时间i的状态，令e为过程中的某个状态，则：

P(En+1=e|E1=e1,E2=e2,…，En=en)=P(En+1=e|En=en)

(4)

存在n种状态的状态空间表示为：

E=[E1E2…En]

(5)

(2)构造概率矩阵.对于式(5)的n种状态空间，根据式(2)构造概率矩阵.

(3)确定状态矩阵.状态矩阵为预测对象的初始值，每种状态对应一个初始值，E0i表示第i种状态的初始值，则n种状态的状态矩阵表示为：

E0=[E01E02…E0n]

(6)

(4)预测数据计算.预测数据计算采用递推方法，第1期的预测值等于基期的状态矩阵乘以概率矩阵，第2期的预测值等于第1期的状态矩阵(预测值)乘以概率矩阵，……，第m期的预测值等于第m-1期的状态矩阵(预测值)乘以概率矩阵.第1期预测数据的计算公式为：

(7)

预测数据计算的递推公式为：

(8)

(5)预测结果分析.对预测结果进行分析，提出相应的政策与对策建议.

3预测实例与结果分析

现对某高校未来五年的师资结构进行预测.现行高校的师资结构从高级到低级分为“教授、副教授、讲师、助教”四种，每年都有一定比例的低一级职称向高一级职称晋升，但不能跃级晋升，即只能晋升一级；根据新的绩效考核管理办法，如果在某一级考核不合格，降到相临的下一级.各级职称每年都有一部分教师退休或调离.每年向社会招聘或引进一定数量的人员以补充教师队伍.按照马尔柯夫模型的预测过程预测如下：

(1)构建状态空间E.根据以上的描述，系统状态空间为E={E1,E2,E3,E4,E5,E6}，其中，E1表示招聘或引进，E2表示教授，E3表示副教授，E4表示讲师，E5表示助教，E6表示退休或调离.

(2)构造概率矩阵P.根据历史统计数据得到概率矩阵.为了数据表达清晰，概率矩阵采用表格的方式，如表1所示.

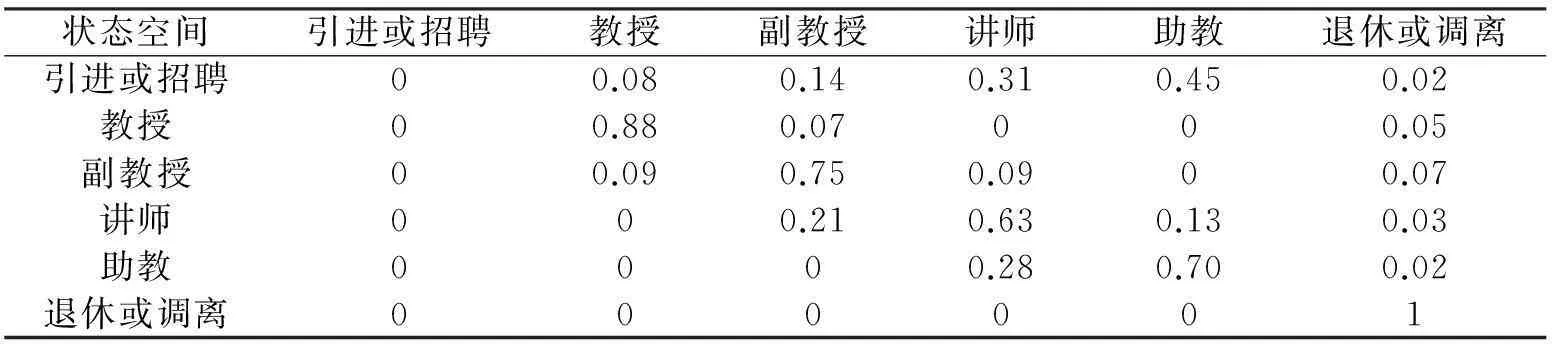
表1　某高校师资结构预测概率矩阵

从表1的数据可以看出，在引进或招聘的教师中，有8%的教授、14%的副教授、31%的讲师、45%的助教，2%当年即调离；“教授”职称的教师中，88%仍然是教授，7%降级为副教授，5%退休或调离；“副教授”职称的教师中，10%晋级为教授，74%仍然是副教授，9%降级为讲师，7%退休或调离.状态空间的其他状态描述略.

(3)确定状态矩阵 .该高校在预测第一年年初，教师总数为1827名，其中教授311名，副教授712名，讲师566名，助教238名，每年计划引进或招聘150名，根据这些数据确定的状态矩阵为E0=[1503117125662380].

根据递推公式(8)，预测2～5年各年末的师资结构，预测结果如表2所示.

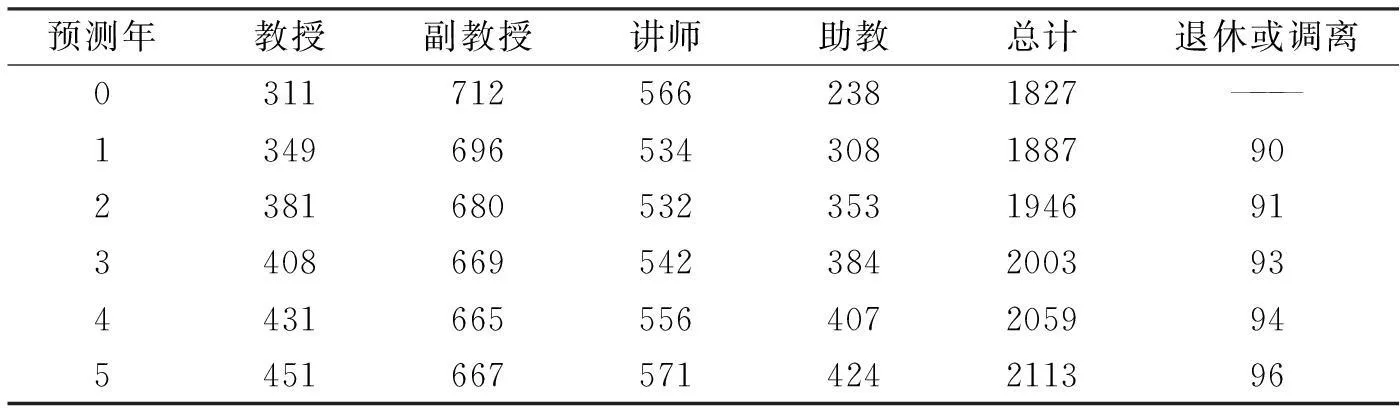
表2　某高校师资结构预测结果

(5)预测结果分析.从表2的预测结果可以看出：退休或调离教师数量每年基本平衡并略有增长，表明教师队伍保持稳定；教师总数(总计)逐年增长，年增长率为3%左右，基本符合教师发展规划要求.但随着高校招生人数减少，对引进教师数量应适当控制；教授和助教的数量增长较快，副教授和讲师的数量有下降趋势，呈现出“两头增长、中间下降”的格式，这不符合人才的发展规划和目标.构建“橄榄球”式的师资结构更适合高校发展的需要〔12〕，因此，要适当调整政策，适当减少副教授晋级教授的比例，增加助教晋级讲师的比例，以使各类职称教师数量均衡发展.

4 结束语

构建良好的师资队伍结构是高等教育改革的主要任务，对于促进高等教育可持续发展、形成高校持久性的竞争优势和提高人才培养质量等方面具有重要作用〔13〕.为了高校师资结构配置的合理性，基于马尔柯夫理论建立了预测模型.结果表明，该预测模型可以有效地提高预测精度，为高校师资结构预测提供了一条新途径.但由于系统各种状态的相互转移不是一成不变的，因此马尔柯夫模型适用于短期预测.由该模型对未来五年某高校的师资结构进行预测，预测结果可作为高校和教育主管部门优化教师结构、制定职称评定政策、促进教师职业发展的重要依据.将研究结果应用于高校师资结构预测，必将得到更精确客观的预测结果，从而促进高校师资水平的整体提高.

参考文献：

〔1〕XIE N M,YUAN C Q,YANG Y J.Forecasting China′s energy demand and self-sufficiency rate by grey forecasting model and Markov model〔J〕.International Journal of Electrical Power & Energy Systems,2015,66(3): 1-8.

〔2〕豆丁网.马尔柯夫预测法[EB/OL].[2015-7-10].http://www.docin.com/p-49100227.html.

〔3〕赵海华.浅谈高校师资队伍建设的问题和对策〔J〕.教育与职业,2014,97(36): 61-63.

〔4〕Holger Kömm,Ulrich Küsters.Forecasting zero-inflated price changes with a Markov switching mixture model for autoregressive and heteroscedastic time series〔J〕.International Journal of Forecasting,2015,31(3): 598-608.

〔5〕百度文库.马尔柯夫预测[EB/OL].[2015-7-10].http://wenku.baidu.com/link?url=Q7lN_uJdGqYBhEdsLAOx6QVWI-cl5P-DRRT57X8Qz3Yrm7eGdcVybYPglva4JL8G4ukXxwy7etFv4dC22R-Zfr7wHxNQ8XM2G8Y0lh8dJ5a.

〔6〕樊国敬.基于马尔可夫模型的旅游目的地人数预测〔J〕.统计与决策,2010,28(21): 98-100.

〔7〕SONG Z,JIANG Y,ZHANG Z J.Short-term wind speed forecasting with Markov-switching model〔J〕.Applied Energy,2014,130(8): 103-112.

〔8〕CARPINONE A,GIORGIO M,LANGELLA R,et al.Markov chain modeling for very-short-term wind power forecasting〔J〕.Electric Power Systems Research,2015,122(5): 152-158.

〔9〕魏国孝,李文华.基于马尔可夫模型的高校师资队伍预测方法〔J〕.宁夏大学学报(自然科学版),2004,25(3): 309-310.

〔10〕Bruno Damásio,João Nicolau.Combining a regression model with a multivariate Markov chain in a forecasting problem〔J〕.Statistics & Probability Letters,2014,90(7): 108-113.

〔11〕SUH J H.Forecasting the daily outbreak of topic-level political risk from social media using hidden Markov model-based techniques〔J〕.Technological Forecasting and Social Change,2015,94(5): 115-132.

〔12〕张晓旭.地方高校师资队伍建设与优化研究〔J〕.国家教育行政学院学报,2014,16(4): 38-42.

〔13〕李颖,孙健鹏.战略性人力资源管理与高校师资队伍建设探析〔J〕.科技与管理,2013,15(2): 119-122.

Prediction on teachers structure of university based on Markov model

GAO Lu

(Center for Teaching Reform and Teaching Quality Assessment,Bohai University,Jinzhou 121013,China)

Abstract：Teaching faculty is the mainstay of colleges and universities.Sound teaching staff structure is the foundation and prerequisite for sustainable development of colleges and universities.In order to promote the rational allocation of the teaching staff structure,the paper studied the forecasting process and made a detailed introduction of the calculation method of each step based on the principle of Markov model.Then it forecasted and analyzed the results of the college′s teaching staff in the next five years.The results showed that the forecasting model may effectively improve the prediction accuracy.Because of the mutual transition probabilities of various system state change frequently,this method is more applicable for short-term prediction.

Key words：Markov model; university; teachers structure; prediction

收稿日期：2015-10-10.

基金项目：2015年辽宁省教育科学“十二五”规划一般项目(No:JG15DB034).

作者简介：高路(1976-)，男，助理研究员，主要从事高等教育管理方面的研究.

通讯作者：36652078@qq.com.

中图分类号：N949

文献标志码：A

文章编号：1673-0569(2016)02-0112-05